1.はじめに
この投稿は下記の記事の続きです。
【質点の回転運動】複素数の助けを借りて楽々理解 - Qiita
以下では「前記事」と呼びます。
前記事では、二次元の物理現象を、一般的に用いられている難解なベクトル解析に頼らずに、複素数だけを使って容易に理解しようという提案をしました。しかし、何とはなしに胡散臭さが漂うらしく、避けられているような雰囲気も感じます。ここでは、前記事の中で導いた複素数の式をそのままシミュレーションに適用し、「広く世間に認められている結果と一致する」ことを示してみようと思います。これにより、胡散臭さが消えて、複素数が広く便利に利用されるようになれば本望です。とは言いながら、適用範囲を自己流に拡大して痛い目に遭い、「お前の責任だ!」と抗議されても困ります。そこで、「おわりに」の項で、複素数方式の適用の限界についても考えてみようと思います。
さて、物理シミュレーションといえば、ルンゲクッタ法などの数値計算によって微分方程式を解くのが一般的です。しかし、ここでは、先ずは MATLAB 製品ファミリーの Simulink によるシミュレーションを行います。Simulink を使えば、画面上に機能ブロックを並べて、それらを信号線で接続してブロック線図を作るだけで、解くべき微分方程式の全情報を盛り込むことができます。そのため、数値解析の知識が十分でなくても、直観的にシミュレーションを行うことができます。また、「複素数推し」の前記事を支援するかのように、定数や変数を複素数のままで扱えるという便利さもあります。
しかし、Simulink だけで済ませてしまうのでは、やはり、複素数方式の汎用性に疑問を持たれそうです。並行して、素の MATLAB によるルンゲクッタ法(ode45)でもシミュレーションしてみます。実は、事前に Simulink のテクニックを知っておいた方が、ルンゲクッタ法の基礎となる状態方程式化への移行が理解しやすくなります。
【この記事のシミュレーション環境】
Windows 10 Home, 執筆途中から Windows 11 Home
(ゆえに、両者による挿図が混ぜこぜです)
MATLAB & Simulink R2019a Home
(オブションの Toolbox や Blockset は使いません)
2.回転座標(基本編)
2.1 準備
前記事では、回転座標上の運動方程式として下記が成り立つことを導きました。
ただし、
$\boldsymbol{r}$, $\boldsymbol{v}$, $\boldsymbol{a}$, $\boldsymbol{F}$ : 複素数で表した 質点の位置, 速度, 加速度, 力 のベクトル
$t$, $m$, $\omega$, $\color{red}{\boldsymbol{i}}$ : 時間, 質点の質量, 回転座標の角速度, 虚数単位
[ $'$ ] あり/無し : 回転座標上/静止座標上 で観測した値
$\boldsymbol{F}'$ : 見掛けの力まで含んだ、回転座標上で質点に掛かる合成力
$\boldsymbol{F}_s$ : 質点に掛かる実在の力$\boldsymbol{F}$ のうち、静止座標系で記述したもの
$\boldsymbol{F}'_r$ : 実在の力$\boldsymbol{F}$ のうち、回転座標系で記述したもの
$-\color{red}{\boldsymbol{i}}2m\omega\boldsymbol{v}'$ : コリオリの力
$m\omega^2\boldsymbol{r}'$ : 遠心力
$$
\frac{d\boldsymbol{r}'}{dt}=\boldsymbol{v}'\tag{1}
$$
$$
\frac{d^2\boldsymbol{r}'}{dt^2}=\boldsymbol{a}'\tag{2}
$$
$$
\boldsymbol{F}'=m\boldsymbol{a}'\tag{3}
$$
$$
\boldsymbol{F}'=\boldsymbol{F}_se^{-\color{red}{\boldsymbol{i}}\omega t}+\boldsymbol{F}'_r-\color{red}{\boldsymbol{i}}2m\omega\boldsymbol{v}'+m\omega^2\boldsymbol{r}'\tag{4}
$$
(4)式は前記事中の(6)式に相当するものです。(1),(2),(3)式については、前記事中で式番号は振られていませんが、(6)式に先行する文中にインラインで記述されています。
これらの式をブロック線図として表現するには、シミュレータ一般に見られる次のような弱点を克服しなければなりません。
弱点1.一度に2階以上の微分は受け付けない
弱点2.実は1階微分さえも苦手、積分なら得意
弱点3.でも、複素数の積分はお断り
弱点1の克服のために、例えば、2階微分 $\boldsymbol{a}'{=}d^2\boldsymbol{r}'/dt^2$ の場合には、$\boldsymbol{v}'{=}d\boldsymbol{r}'/dt$ と $\boldsymbol{a}'{=}d\boldsymbol{v}'/dt$ のように二つの1階微分に分解します。これを(2)式に適用し、重複した式や、$\boldsymbol{F}'$ など補助的な変数を消去すると次の(5)式のようになります。微分記号は1階のものだけに統一され、数式の数も減りました。
$$
\left\{
\begin{align}
&\frac{d\boldsymbol{r}'}{dt}=\boldsymbol{v}'\\
&\frac{d\boldsymbol{v}'}{dt}=\boldsymbol{a}'\\
&\boldsymbol{a}'\color{#bbb}{\left(=\frac{\boldsymbol{F}'}{m} \right)}=\frac{\boldsymbol{F}_s}{m}e^{-i\omega t}+\frac{\boldsymbol{F}'_r}{m}-i2\omega\boldsymbol{v}'+\omega^2\boldsymbol{r}'
\end{align}
\right.\tag{5}
$$
さて、一般の物理現象における原因と結果の関係を考えてみると、下記のように、原因を積分して順次に結果を得るという循環になっていることが分かります。
力 $\boldsymbol{F}$ が働く(加速度 $\boldsymbol{a}$ が決まる) →[積分]→ 速度 $\boldsymbol{v}$ が決まる
→[積分]→ 位置 $\boldsymbol{r}$ が決まる(その位置での新たな力 $\boldsymbol{F}$ が決まる)
( → 元に戻って繰り返す )
ところが、(5)式は、結果を微分して原因を知るような表現になっています。これでは上記の流れに逆行して不自然です。実際に微分を使ってブロック線図を描こうとしても、信号線の繋ぎようがなく途中で行き詰まってしまいます。ここは、積分を使用するのが正道です。
確かに、シミュレータ類の微分の機能は不完全で、Simulink でも同様です。しかし、実のところ、その対策のために得意技の積分に乗り換えようと考えた訳ではありません。本当の理由は、上記のように、原因を積分して結果を得る流れの方が自然だからです。それなのに、ついつい、弱点2の表現の方が受けが良さそうだという邪心がわき、少々ひねってしまいました😅。
この濡れ衣ともいえる弱点2の克服のためには、例えば $\boldsymbol{v}'{=}d\boldsymbol{r}'/dt$ と表現された式は、逆向きに $\boldsymbol{r}'{=}\int_0^t\boldsymbol{v}'dt{+}\boldsymbol{c}$ であると解釈します($\boldsymbol{c}$ : 積分定数, 初期値)。(5)式にこれを適用すると次のようになります。式の順番は、ブロック線図の描画手順に沿うように意図的に並べ替えてあります。微分記号はなくなり、単積分だけになりました。
$$
\left\{
\begin{align}
&\boldsymbol{a}'=\frac{\boldsymbol{F}_s}{m}e^{-i\omega t}+\frac{\boldsymbol{F}'_r}{m}-i2\omega\boldsymbol{v}'+\omega^2\boldsymbol{r}'\\
&\boldsymbol{v}'=\int_0^t\boldsymbol{a}'dt+\boldsymbol{c}_1\\
&\boldsymbol{r}'=\int_0^t\boldsymbol{v}'dt+\boldsymbol{c}_2
\end{align}
\right.\tag{6}
$$
Simulink では、積分器として、図1[A] の左上にある $\bbox[2px,border:1px solid black]{\smash[b]{1/s}}$ ブロックを使用します。これにより数式 $S_{out}{=}\int_0^t S_{in}dt{+}c$ の演算を行うのですが、既定では $c{=}0$ なので、$S_{out}{=}\int_0^t S_{in}dt$ と等価になります。ところが残念なことに、(6)式の被積分関数の $\boldsymbol{a}'$ や $\boldsymbol{v}'$ が複素数であるのに対し、この積分ブロックの $S_{in}$ の型は実数だけに限られています。図1[A]には、この記事で差し当って使用するいくつかの機能ブロックを表示(日本語名は私の非公式造語)していますが、積分ブロック以外で複素数を扱えないのは時間ブロックだけです。時間が実数であることは当然としても、積分ブロックが複素数を扱えないのは、当記事にとって大変な痛手です。
そこで、この弱点3の克服のために、複素数でも扱える特製の積分ブロックを自作します。自作といっても難しいものではなく、図1[B] のように、既製のブロックを組み合わせたものを範囲選択し、1つのブロックとして登録(サブシステム化)すれば完了です。このサブシステム上をダブルクリックすれば、別タブが開いて中身の詳細ブロック線図が表示され、機能を再確認することができます。これで、複素数を気兼ねなく扱える環境が整いました。
(6)式が表す関係を、図1の[A]と[B]のブロックを組み合せて図示すると、図1[C] のようなブロック線図になります。この中には、[A]とは形が異なるブロックも混じっています。しかし、加減算や乗除算のブロックは、入力点数や各点の演算記号を自由に設定し、必要に応じて形やサイズも変えて使用することができます。その点を意識して柔軟に解釈できれば大丈夫です。定数やゲインなどの値は、そのブロックをダブルクリックし、開いた小窓から入力します。入力した文字列が長すぎるときには「-C-」と略されますが、ブロックのサイズを拡大すれば入力通りに表示できます。
一見すると、このブロック線図はかなり複雑に見えますが、図中に付記した変数を (6)式と対比してみれば、余計な説明はなくても自然な流れで理解できるものと思います。これでシミュレーションの中心部分はほとんど出来上がったことになります。

図1[C]をベースにして周辺機能を追加し、シミュレーションのための最終的なブロック線図を描きます。まず、その前の準備として、これから新たに使用する図2[A] の機能ブロックの説明をしておきます。これらは、ライブラリブラウザの中に収められているブロックの一覧から、ドラッグ&ドロップで自由に取り出してくることができます。

絶対値については特に説明の必要はないでしょう。二乗のプロックは既に図1でも紹介していますが、実は、ライブラリブラウザの中を目を皿のようにして探しても見つかりません。准汎用的な Math Function ブロック(既定では $e^u$)の設定を square($u^2$)に変更することで作ることができます。大小比較は、2つの入力(上や左の入力端子が左辺、他方は右辺)の大小関係が、ブロック中に示されている記号($\gt$,$=$,$\lt$ など)を満足するときに論理値 true を出力します。MATLAB Function は、ブロックの単純な組合せでは表現できない機能や、表現できても複雑になり過ぎる機能を MATLAB のスクリプトによって記述するブロックです。ブロックをダブルクリックすると、登録したスクリプトが 図2[B] のように表示されます。便利ではありますが、シンボルを見ただけでは中身が分からないので、多用しすぎると可視化に逆行します。
停止は、その入力が true になったとき、シミュレーションの途中でも実行を中断させます。終端器は、ブロックの出力端子に接続して、その信号を使用しないことを宣言します。使用しない出力端子でも、それを解放したままシミュレーションすると警告が出ます。線なし接続は、その間に信号線が引かれていなくても、同一タグ名の Goto から From の向きに信号が伝わります。信号線が入り乱れて混乱しそうな場合に利用します。これも使い過ぎると分かり難くなります。バスの入出力は、複数の信号線を1本にまとめて整理するために使います。図中には示していませんが、他に、これとシンボルが似ている マルチプレクサの入出力(Mux, Demux)というものもあります。しかし、複素数を扱いにくいので、この記事では使用をお薦めしません。
次に続くブロックは、全てシミュレーションの結果を観測するためのものです。オシロスコープ は、横軸を時間軸にしたマルチチャンネルの計測器です。XY スコープは、x入力を横軸、y入力を縦軸にした計測器です。どちらも、機能ブロックとは別の位置に小窓が開いて、シミュレーション実行中の出力波形をリアルタイムで表示します。なお、MATLAB の figure は、グラフの座標スケールを自動で最適化してくれるので便利ですが、Simulink の XY スコープにはその機能がありません。ブロックをダブルクリックして、事前に見繕った適度な座標スケールを設定してやる必要があります。
なお、本記事中では使用していませんが、「オシロスコープ」と類似の「シミュレーションデータインスペクター」や「フローティングスコープ」という機能もあります。これを使えば、信号線の接続なしでも、予め指定しておいた信号のシミュレーション波形を表示できて便利です。ただし、「XY スコープ」的な使い方はできません。
Simulink→MATLAB中継は、シミュレーション結果のデータを MATLAB に送るインタフェースです。シミュレーションのデータはオシロスコープや XY スコープの画面にも表示できますが、そのフォーマットは既定の簡素なものだけで、見映えはあまり良くありません。試行を繰り返すだけの初期段階であれば、Simulink だけでも十分に目的は達せられますが、様式を整えた図形にするには MATLAB の豊富な描画機能を使う必要があります。その場合のインタフェースとして使用します。
ブロック線図上に陽には表示できませんが、もちろん、逆向きの MATLAB→Simulinkの操作も可能で、各ブロックのパラメータの書き替えや、シミュレーションの開始・終了の指示に利用します。これらも、初期段階の試行だけであれば、 Simulink 上の操作だけで事足りますが、条件を変えながら繰り返しシミュレーションするときなどには、MATLAB スクリプトとの共演が大いに役に立ちます。なお、Simulink は MATLAB 上で動作するツールなので、Simulink 動作中は MATLAB も必ず動作しており、常に共演可能な状態でスタンバイしています。
2.2 最終的なブロック線図
図1[C]にいくつかの機能ブロックを追加して、回転座標の基本的な動作をシミュレーションするためのブロック線図を図3のように作成しました。このシミュレーションの目的は「【静止座標上で等速直線運動している質点】を回転座標から観測する」ことです。この図には、ブロック線図だけでなく、周辺部も含むPCの全画面を収め、Simulink のシミュレーション環境の雰囲気を感じ取れるようにしています。
追加機能を組み込むスペースを確保するために、基本部分のブロックの配置や構成が図1[C]からは若干変わっていますが、表現しようとしている動作は全く同じです。また、Qiita 映えを狙ってブロックに色をつけました。積分がピンク、乗除算関係が黄色、複素数の変換が緑色です。「 MATLAB からのパラメータの変更」を意図しているブロックは水色にしています。

図3で新たに追加された機能を説明します。薄紫色の背景で囲まれた部分は座標変換のためのものです。このシミュレーションでは、静止座標上で質点が等速直線運動しているだけですから、実在の力は一切存在しません($\boldsymbol{F}_s{=}0$、$\boldsymbol{F}'_r{=}0$)。したがって、回転座標から見る質点の軌跡は、運動方程式を解くまでもなく、この座標変換だけで求めることができます。ここで求めた位置 $\boldsymbol{r}_c'$ の軌跡は、このシミュレーションの模範解答として、運動方程式による結果との比較のために使用します。
水色の三角形のゲインブロック Cor や Cf は、この値を 0 に設定変更することで、コリオリの力や遠心力などの見掛けの力を考慮しないときの軌跡も、参考のために確認してみることができます。
図1[C]で $\boldsymbol{c}_1$, $\boldsymbol{c}_2$ と表現していた初期値の値は、具体的な速度の初期値 $\boldsymbol{v}_0'$ と位置の初期値 $\boldsymbol{r}_0'$ に置き換えてあります。前記事の流れから、静止座標と回転座標の軸が一致する瞬間を $t{=}0$ としているので、回転座標上の位置の初期値 $\boldsymbol{r}_0'$ は、静止座標上の初期値 $\boldsymbol{r}_0$ と一致します。もう一つの 回転座標上の速度の初期値 $\boldsymbol{v}_0'$ は少々複雑で、座標変換部(薄紫色の部分)の出力として得られる位置 $\boldsymbol{r}_c'$ の式を利用して次のようにして求めます。
$$
\boldsymbol{v}_0'={\left.\frac{d\boldsymbol{r}_c'}{dt}\right|} _{t=0}
$$
$t{=}0$ を代入する前の右辺の式は次のようになります。(ただし、$\boldsymbol{v}$: 静止座標から見た等速直線運動の速度ベクトルを複素数表現したもの)
$$
\begin{align}
\frac{d\boldsymbol{r}_c'}{dt}&=\frac{d}{dt}\{(\boldsymbol{v}t+\boldsymbol{r}_0)e^{-i\omega t}\}\\[1ex]
&=\{\frac{d}{dt}(\boldsymbol{v}t+\boldsymbol{r}_0)\}e^{-i\omega t}+(\boldsymbol{v}t+\boldsymbol{r}_0)\frac{d e^{-i\omega t}}{dt}\\[1ex]
&=\boldsymbol{v}e^{-i\omega t}-i\omega(\boldsymbol{v}t+\boldsymbol{r}_0)e^{-i\omega t}
\end{align}
$$
これに $t{=}0$ を代入することにより、$\boldsymbol{v}_0'{=}\boldsymbol{v}{-}i\omega\boldsymbol{r}_0$ となります。図3の初期速度 $\boldsymbol{v}_0'$ の値はこの式をブロック線図化することで生成しています。
積分ブロックの初期値の設定は、ブロックの出力に明示的に足し込む図3のような方法以外に、積分ブロックの内部パラメータとして陰に設定することもできます。しかし、図3の方式の方が、初期値として複素数をそのまま使うことができるうえ、その算出根拠まで可視化できるため、読む人には理解しやすくなります。ただし、「初期」値とはいっても、シミュレーションが始まる時点だけに必要な情報という訳ではありません。シミュレーションが終わるまで、初期の一定値を保ち続ける必要があります。(詳細は割愛しますが、リミッタ付き積分などのときには、内部で陰に設定する方が都合が良いケースもあります。)
図3の右上隅にあるのは、XYスコープと MATLAB へのインタフェースです。この図では、MATLAB インタフェースには時間のデータ $t$ は接続されていません。しかし、接続が明示されている他の信号( $\boldsymbol{r}'$ や $\boldsymbol{r}_c'$ )の付属情報として自動的に送出されるようになっています。
2.3 いよいよシミュレーション
図3の Simulink の画面上で、シミュレーション終了時間を設定し実行ボタン▶をクリックすると、シミュレーションが始まり、XYスコープ画面上に「回転座標から観測した質点の軌跡」がリアルタイムに表示されます(図4)。
サンプル時間が無指定の場合、Simulink はこれを自動で決めてくれます。計算誤差が規定値に収まる範囲内で、その時々に許されるできるだけ長い時間が選ばれます(可変ステップ)。そのため、個々の点での正確さは確保されている場合でも、グラフのプロットの間隔が空きすぎて、折線感が目立ってしまうことがあります。そのときには、Simulink→MATLAB中継(To Workspace)やスコープ類などのどれか一つのブロックをダブルクリックし、「サンプル時間」欄に適度な短めの時間を設定します。

さて、以上によりシミュレーションは実行できたものの、一つのケースだけで終ってしまいました。これでは十分なデータが得られないので、MATLAB と連携させて多くのケースについてシミュレーションを行い、形式を整えて描いた軌跡を図5に示しています。等速直線運動の出発点や速度は同一にして、移動方向だけを様々に変化させた結果を示しています。ここで使った MATLAB のスクリプトは、この記事の末尾の「プログラム」欄に添付しています。MATLAB からのパラメータの変更法や、Simulink からのデータの取り込み方法の詳細については、そちらの方を参照ください。
なお、Simulink のブロック線図のファイルと、MATLABのスクリプトファイルの拡張子は、それぞれ .slx と .m のように異なります。そのため、同一のベース名でも両ファイルの区別は可能だと思いがちですが、ベース名の重複はエラーになるので注意が必要です。

図5のシミュレーションの条件は、前記事に掲載した図のものとは少々異なります( 78[rpm], 0.5[m/s] )が、着目すべき点は同一で次の2つです。
① 座標変換で求めた紺色の軌跡と、運動方程式から求めたピンク色の軌跡が良く一致している。
② コリオリの力と遠心力の両方を考慮しなければ正しい結果は得られない。
①と②により、従来からの回転座標系の理論や見掛けの力の理論が正しいことが結論づけられます。しかし、それだけでは「何を今更」のレベルの話にしかなりません。私がここで強調したいのは、複素数を使うだけでベクトル解析と同一の結果を容易に導けたということです。ただ、この種の面白みのない基本的な軌跡はあまり見掛ける機会もないため、類似例を挙げたうえで「広く世間に認められている結果と一致する」などと したり顔ができないのが残念です。しかし、運動方程式による計算結果が、座標変換による模範解答の軌跡にピッタリと一致しているわけですから、疑う余地のない真実ではあります。
2.4 実在の力も考慮
図5の軌跡は、運動方程式の中の重要な要素である $\boldsymbol{F}'_r$ と $\boldsymbol{F}_s$ が存在しない条件でシミュレーションした結果です。これだけでは、(6)式が正しいことを示せたとは言えません。そこで、これらの力も考慮してシミュレーションし、式の正当性を最終確認してみようと思います。
そのために、図3のブロック線図を少々描き変えた図6を使用します。動作の基本は変わりませんが、静止座標上の現象を回転座標から観測していたという立場から、回転座標系の上だけで現象を記述しようという見方に変わっています(初期値 $\boldsymbol{v}'_0$ の与え方が図6よりも簡単になります)。ただ、シミュレーション結果を吟味するときには、これを静止座標から再観測した方が都合が良いので、そのための座標変換機能も持たせています。
シミュレーションの対象は、暗算のしやすさを考え、1 [rad/s] の角速度で回転している座標上で、回転の中心から 10 [m] 離れた位置に置かれた 1 [kg] の質点の運動とします。この質点は、当初は回転座標上で動けないように拘束されていますが、回転座標と静止座標の軸が一致した瞬間($t{=}0$)に拘束を解かれるものとします。その拘束が解かれた瞬間から、質点は実在の力の支配を受け始めます(実在の力は当初から存在していたものの、拘束力によって打ち消されていたと考えます)。なお、拘束されていた質点も、静止座標から見れば回転運動しているので、その接線方向に初期速度を持っています。シミュレーション結果の軌跡を吟味するときには、回転座標上の初期速度 $\boldsymbol{v}_0'$ は 0 でも、静止座標から見た初期速度 $\boldsymbol{v}_0$ は $i\omega\boldsymbol{r}_0$ であることに留意しておく必要があります。(前記事で説明したように、$i$ を掛けることによって、反時計回りに 90° 向きを変えたベクトルを表現することができます)

$\boldsymbol{F}'_r$ と $\boldsymbol{F}_s$ を同時に考慮すると質点の運動が複雑になり過ぎます。そこで、まずは $\boldsymbol{F}_s$ は 0 とし、回転座標上で実軸方向を向いた力 $\boldsymbol{F}'_r$ だけを考え、この大きさを種々に変えた場合のシミュレーション結果を図7に示します。
応用面で実益のありそうなモデルではないため、ネットを見渡しても、衆知の模範波形のようなものは見当たりません。しかし、多くのケースを整理して図7のように並べて観察してみれば、これらが理に適った結果であることは容易に確認できます。

本シミュレーションの目的は、回転座標上での質点の軌跡(青色)を求めることです。しかし、結果の妥当性を理解するには、静止座標から見た軌跡(赤色)を基準にして考えるのが近道です。$\boldsymbol{F}_r'$ は回転座標上では一定方向を向いた一定量の力ですが、これを静止座標から見ると、質点を作用点としてその周りを旋回する力 $\boldsymbol{F}_r{=}\boldsymbol{F}_r'e^{i\omega t}$ になります。これによる、$t$ 秒後の静止座標上の質点の速度変化 $\mathit{\Delta}\boldsymbol{v}$ と位置変化 $\mathit{\Delta}\boldsymbol{r}$ は次のようになります。
$$
\begin{align}
&\mathit{\Delta}\boldsymbol{v}=\frac{\boldsymbol{F}_r'}{m}\int_0^te^{i\omega t}dt=\frac{\boldsymbol{F}_r'}{i\omega m}\left[e^{i\omega t}\right]_0^t=\frac{\boldsymbol{F}_r'}{i\omega m}\left(e^{i\omega t}-1\right)
\end{align}
$$
$$
\begin{align}
\mathit{\Delta}\boldsymbol{r}&=\frac{\boldsymbol{F}_r'}{i\omega m}\int_0^t\left(e^{i\omega t}-1\right)dt=\frac{\boldsymbol{F}_r'}{i\omega m}\left[\frac{1}{i\omega}e^{i\omega t}-t\right]_0^t\\[1ex]
&=\frac{\boldsymbol{F}_r'}{i\omega m}\left\{\frac{1}{i\omega}\left(e^{i\omega t}-1\right)-t\right\}
\end{align}
$$
これより、座標が一回転(時間 $t=2\pi/\omega$)するたびに、それぞれの変化量は次のようになります。
$$
\begin{align}
&\mathit{\Delta}\boldsymbol{v}| _{t{=}2\pi/\omega}=0\\
&\mathit{\Delta}\boldsymbol{r}| _{t{=}2\pi/\omega}=\frac{\boldsymbol{F}_r'}{i\omega m}\left(-\frac{2\pi}{\omega}\right)=i\frac{2\pi\boldsymbol{F}_r'}{\omega^2m}
\end{align}
$$
すなわち、$\boldsymbol{F}_r'$ が存在していても、一周期ごとに見れば速度変化はないので、初期速度 $\boldsymbol{v}_0$ は $i\omega\boldsymbol{r}_0$ そのままに保たれて移動を続け、その結果、一周期ごとに、位置が一定量 $i2\pi\boldsymbol{F}_r'/(\omega^2m)$ ずつ増えて行くことになります。図の左上の $\boldsymbol{F}_r'{=}20{+}0i$ のケースについて、シミュレーション条件を代入して一回転ごとの移動量を確認してみると、次の式のようになります。($T$ : 回転周期 $2\pi/\omega$)
$$
\begin{align}
\text{移動量}&=\boldsymbol{v}_0T+i\frac{2\pi\boldsymbol{F}_r'}{\omega^2m}\\[1ex]
&=i\omega\boldsymbol{r}_0\frac{2\pi}{\omega}+i\frac{2\pi\boldsymbol{F}_r'}{\omega^2m}=i2\pi\left(\boldsymbol{r}_0+\frac{\boldsymbol{F}_r'}{\omega^2m} \right)\\[1ex]
&=i2\pi(10+20/1)=i188.5\text{ [m]}
\end{align}
$$
この値は、図の赤色の軌跡の変動周期(距離)と一致しています。この軌跡を回転座標から観測するので、青色の軌跡の渦巻きのピッチはほぼ一定に保たれます。なお、$\boldsymbol{F}_r'{=}{-}10{+}0i$ では移動量が 0 となるため、青色の軌跡は渦を巻かず半径 10[m] の固定円になります(図示はしていません。代わりに $\boldsymbol{F}_r'{=}{-}(10{\pm}3){+}0i$ での軌跡を掲せています)。
次に、回転座標上では $\boldsymbol{F}_r'{=}0$ として、静止座標上で虚軸方向に力 $\boldsymbol{F}_s$ が働く状態を想定し、その大きさを変化させた場合の軌跡を図8に示します。この場合、静止座標上では、虚軸方向を向いた初期速度に、同方向あるいは逆方向の加速度が加わるだけのシンプルな運動になります。

図の上半分では、質点は初期速度と同方向に加速され続け、赤色の線上を移動するので、渦巻きのピッチは加速度的に広がっていきます。図の下半分では、力の方向が逆になるので、始点から赤色の線に沿って上に向かっていた質点が、途中で向きを反転し下向きに加速を始めます。この過程で青色の軌跡は複雑な形状を呈しますが、元の始点を通り過ぎれば、上半分と同様、渦巻きのピッチは加速度的に広がっていきます。
これで、複素数で表した(6)式の妥当性がすべて確認できたことになります。(少々強引?(^_^;)。ご指摘事項があればコメントをお願いします。)
蛇足: Simulink は、ブロック線図を描くだけで効率良くシミュレーションできるところが長所ですが、図を芸術的に美しく描くことに拘り始めると、手間が掛かり過ぎて作業効率が低下し、本末転倒になってしまいます。図3は Qiita の晴れ舞台で披露するために時間を掛けて丁寧に描いていますが、図3と構成が同一であれば、図9のような乱雑なブロック線図でも問題なく動作します。あまり凝りすぎないことが肝要です。「自動配置」の機能もありますが、作図領域が大幅に広がるので扱い難くなります。やはり、ある程度の人手による手直しは必要です。

2.5 ルンゲクッタ法による数値解析
以上で、回転座標系の基本的な運動方程式の Simulink によるシミュレーションは終わりました。次に、既述と同一のモデルをルンゲクッタ法で解く手順について考えます。常微分方程式(Ordinary Differential Equation...ODEと略)を解く方法は多数ありますが、ルンゲクッタ法はそれらの総称として使われる場合もあれば、狭義で4次のルンゲクッタだけを指す場合もあります。MATLAB で一押しされている解法は ode45 ですが、これは、4次のルンゲクッタに5次の要素を加えて改良された方法だそうです。ここでもこれを使います。
実は、 Simulink も、舞台裏ではルンゲクッタ法を利用してシミュレーションしています。図3の右下隅に小さく「 ode45 」という文字が見えます。解法(ソルバー)としては、「シミュレーション」>「モデル コンフィギュレーション パラメータ」の設定欄で「可変ステップ」の「自動」を指定しているだけですが、Simulink が気を利かせて ode45 を見繕って解いてくれているようです。ということで、解析手法を Simulink からルンゲクッタに乗り変えるといっても、全く異なる解法で考え直すという訳でもありません。結局、裏でやっていることは同じです。
手順1
Simulink のブロック線図の中の全ての積分ブロックに着目し、それぞれについて、初期値を足し込んだあとの出力信号のシンボル名を拾い出します。(そのシンボル名の信号をここでは状態変数と呼ぶことにします。)
これらの変数は、複素数対応の積分ブロックの出力であれば複素数であり、一般の積分ブロックの出力であれば実数です。ここでは取敢えず、複素数か実数かの区別なく、これらを単に $y_1,y_2,y_3,...$ と置きます。図3の例では、例えば、$y_1{=}\boldsymbol{r}'$、$y_2{=}\boldsymbol{v}'$ となります。$y_1$, $y_2$ のそれぞれにどの状態変数を割り付けるのかは自由です。
手順2
それぞれの状態変数について、その1階微分が表す式を次のように作ります(Simulink で使った最終式である(6)式を、1ステップ前の(5)式に準じた形に戻す感じになります)。ここでは、この方程式を状態方程式と呼ぶことにします。
$$
\left\{
\begin{align}
&dy_1/dt=f_1(t,y_1,y_2, ...,y_n)\\
&dy_2/dt=f_2(t,y_1,y_2, ...,y_n)\\
&\hspace{5em}\vdots\\
&dy_n/dt=f_n(t,y_1,y_2, ...,y_n)\\
\end{align}
\right.\tag{7}
$$
(7)式は、MATLAB ヘルプセンターの「ODE ソルバーの選択」に記載されているのと同様の式です。右辺があまりにも一般化されていて難しく見えますが、それほど気にする必要はありません。$dy_1/dt{=}$ などに続けて、必然的に導かれてくる式をそのまま書き下すだけで大丈夫です。$y$ には該当しない信号、例えば、システムへの入力 $u_1,u_2,...$ (図3の例では $\boldsymbol{F}_r'$ $\boldsymbol{F}_s$)などがあれば、これらは定数項や $t$ の関数の一部と解釈してそのまま記述します。なお、積分の式ではないので、$f$ には初期値の情報は含まれません。初期値はあとで別の方法で与えます。
以上により、図3の例では、次のような状態方程式が得られます。
$$
\left\{
\begin{align}
&\frac{d\boldsymbol{r}'}{dt}=\boldsymbol{v}'\\
&\frac{d\boldsymbol{v}'}{dt}=\frac{\boldsymbol{F}_s}{m}e^{-i\omega t}+\frac{\boldsymbol{F}'_r}{m}-i2\omega\boldsymbol{v}'+\omega^2\boldsymbol{r}'
\end{align}
\right.\tag{8}
$$
手順3
状態方程式の内容を ode45 に伝えるには作法があります。例えば、状態方程式が下記であるとき、スクリプト内に次のようなローカル function を作っておきます( (8)式では項が多すぎて複雑なので、一時的に簡単な例に変えています)。
$$
\left\{
\begin{align}
&\frac{dy_1}{dt}=y_2\\
&\frac{dy_2}{dt}=-ay_1-by_2t
\end{align}
\right.
$$
function dydt=state_equ(t,y,a,b)
dydt(1,1)=y(2);
dydt(2,1)=-a*y(1)-b*y(2)*t;
end
dydt は $[dy_1/dt\hspace{1.5ex}dy_2/dt]^\mathrm{T}$ を表す列ベクトルとして記述しなければなりません。行ベクトルでも、機転を利かせて処理してくれれば良さそうなものですが、列ベクトルであることが明確に分かるように表現しないと確実にエラーになります。t は時刻でスカラー量です。y は $y_1$ と $y_2$ を要素とするベクトルですが、MATLAB のヘルプでは、行ベクトルなのか列ベクトルなのか明確ではありません。どちらに想定してプログラミングしても同じように動作します。dydt に対する厳格さとは大違いです。
dydt, t, y という変数名は任意に変更することができますが、MATLAB ヘルプの中の多くの例では、そのまま決まり事のように使われています。これを踏襲しておくのが間違いもなく無難だと思われます。state_equ は私が勝手に命名した関数名です。関数の引数としては、最低でも (t, y) は必要です。それ以外に必要になれば a や b のように、その後ろに書き加えます。しかし、a や b が即値として決まっているのであれば、わざわざ引数として渡すまでもなく、function の中の a, b をその数値で置き換えておけば済むことです。
この function は一般のものとは異なり、ユーザーが意図して直接呼び出せるものではありません。ode45 コマンドを介して間接的に利用されることになります。しかし、実際の計算において、この function がどのような形で利用されるのかを意識しておく方が今後の見通しが良くなります。難しい高次のルンゲクッタではなく、原始的な前進オイラー法を頭において自己流に解釈すると次のとおりです。
- この function は時間ステップ $\mathit{\Delta}t$ ごとに、毎回、ode45 から呼び出される。
- そのとき、引数の t, y には、前(第$N$)ステップでの値 $t_{\Tiny{N}},$, $y_{\Tiny{N}}$ が入っている。
- function は、この値を利用して $(dy/dt)_{\Tiny{N}}$ を計算して dydt として ode45 に返す。
- ode45 はこれを受けて $y _{{\Tiny{N}}{+}1}=(dy/dt) _{\Tiny{N}}\,\mathit{\Delta}t+y _{\Tiny{N}}$ を計算し、y の新値とする。
正確さには欠けますが、このように考えておけば、作法に関するいくつかの疑問点は何となく解消できます。
手順4
手順3で作った function を利用して ode45 を実行するスクリプトは次のようになります。
[t,y]=ode45(@(t,y) state_equ(t,y,a,b),[0 10],[1 0]);
左辺の t は、シミュレーション結果の各サンプリング点の時刻を、縦(上→下)に昇順に並べた列ベクトルとして出力されます。y は、t と同じ行数の行列です。各列が $y_1, y_2, ...$ に対応しており、それらの各行は、同行の t の時刻における $y$ の値になっています。右辺の @(t, y) や 関数の引数 t, y は、状態方程式の function を定義したときの t, y に対応するものですが、定型的な様式と考えておくだけで良いでしょう。
次の [0 10] は「シミュレーションの時間範囲」を指示するベクトルで、[シミュレーション開始時間(秒) 同終了時間(秒)] で表します。この場合、ode45 により、時間の刻み幅がステップごとに自動的に調整されるため、出力のサンブリング時刻列 t は不等間隔になります。そのため、刻み幅が長めの区間では、グラフが折線的に描かれて見映えが悪くなることがあります。
サンプリング時刻列 t を意図的に決めたい場合には、[0 10] の代わりに例えば [0:0.1:10] などとして、希望する時刻列のベクトルをそのまま入力します。この場合、シミュレーション結果は、指定時刻のものしか出力されませんが、内部での刻み幅の自動調整機能は有効に働いているようで、粗いピッチを指定しても計算精度が落ちることはありません。(上記の時間範囲を指示するベクトルは、ヘルプの説明では行ベクトルになっていますが、列ベクトルとして記述しても正常に動作します。)
蛇足: 「シミュレーション開始時間」は 0 に設定するのが普通だと思います。0 以外に設定できることを知って、都合の良い応用例を思い付いたのですが、とんだ見込み違いでした。こんな運用はできませんので御注意ください。 ($t{=}0$ で初期値を与えて、過渡状態が過ぎて定常状態に入ったところからのシミュレーション波形を採取する。)
次の [1 0] は初期値を設定するベクトルです。1つ目が $y_1$ の初期値、2つ目が $y_2$ の初期値です。状態方程式化で行き場を失った初期値情報はここで復活します。(これも、「時間範囲の指定」と同じく、列ベクトルで [1;0] と指示しても正常に動作します)。なお、初期値と聞けば、$t{=}0$ における $y$ の値と受け取るのが自然ですが、「シミュレーション開始時間」の設定を 0 以外の時間に指定した場合には、その時刻における $y$ の値が初期値となります。
さて、MATLAB ヘルプの説明では、状態方程式の各種の記述方法に応じて、下記のような色々な呼び出し方が示されています。個人的にはそんなに頻繁に利用するコマンドでもないので、複雑な利用方法をあれもこれも示されては混乱するばかりです。物覚えが悪い私としては、状態方程式は必ずローカルの function 形式で記述し、呼び出し方法は上記の一本に絞って使うことにしています。引数 a, b などが存在しないケースでも、それらを書かないでおくだけで大丈夫です。
[t,y]=ode45(@rot_coord([0 10],[1 0])); % a,b が無いとき
[t,y]=ode45(@(t,y) 2*t,[0 10],0); % 無名関数で表現されたとき
yprime=@(t,y) 2*t;
[t,y]=ode45(yprime,[0 10],0); % ハンドル名つき無名関数で表現されたとき
手順5(複素数利用の最終ステップ)
普通なら以上で終わるところですが、この記事ではもう一手間が必要になります。実は、手順3の function の dydt や y の値として複素数を使用するとエラーで撥ねられてしまいます。ところが、a や b は複素数でも構わないし、function の中での複素数同士の加減乗除算は問題なくできます。ということは、ode45 と function 間での dydt や y の受け渡し方法さえ工夫すれば、複素数を利用した計算も可能になりそうです。この方針に沿って(8)式を function 化すると次のようになります。function 名の rot_coord は適当に命名したものです。
function dydt=rot_coord(t,y,Ww,Fr,Fs,Mm)
% y(1),y(2): 位置の実部(x成分)と虚部(y成分)
% y(3),y(4): 速度の実部(x成分)と虚部(y成分)
% Ww:角速度、Fr:回転座標の実在の力(複素数)
% Mm:質量、 Fs:静止座標の実在の力(複素数)
r = y(1) + i*y(2); % 実部・虚部に分離して受け取った
v = y(3) + i*y(4); % データを合成して複素数を再現。
% 複素数による状態方程式の記述
drdt = v;
dvdt = Fs*exp(-i*Ww*t)/Mm + Fr/Mm - i*2*Ww*v + Ww^2*r;
dydt = zeros(4,1); % dydt が列ベクトルであることを宣言
dydt(1) = real(drdt); % 複素数として得られた drdt, dvdt を
dydt(2) = imag(drdt); % 実部・虚部に分離してから返す。
dydt(3) = real(dvdt);
dydt(4) = imag(dvdt);
end
一方、これを呼び出す ode45 コマンドは次のようになります。ただし、Rs0 と Vr0 は、事前に複素数形式で設定した「初期位置」と「初期速度」、dT や Ts は事前に数値を代入されている「時間刻み幅」と「終了時間」とします。
[t,y]=ode45(@(t,y) rot_coord(t,y,Ww,Fr,Fs,Mm), ...
[0:dT:Ts],[real(Rs0) imag(Rs0) real(Vr0) imag(Vr0)]);
手順6(実数に限定したときの最終ステップ)
手順5を見て、「そうまでして複素数を使いたいの?」という疑問が湧いた場合は、更に一手間を加えます。複素座標からは離れ、実数の x y 座標だけで考えることになります。ベクトル解析を経由して辿り着いた場合でも、複素数を使って楽々とゴールした場合でも同一の function になります。複素数でやってきた場合には、今まで楽をしてきた分、虚数単位 $\boldsymbol{i}$ を消すための回転操作が必要になります。
具体的に示せば、
- 状態変数や入力変数の実部と虚部を分離する。
- その実部を x 成分、虚部を y 成分とした列ベクトルに置き換える。
- 状態方程式の中の $e^{i\theta}$ や $i$ は回転行列と置き換える。
$$
e^{i\theta}\Longrightarrow
\left[
\begin{array}{cc}
\cos\theta & {-}\sin\theta\\
\sin\theta & \cos\theta
\end{array}
\right]
\hspace{2em}
i=e^{i\pi/2}\Longrightarrow
\left[
\begin{array}{cc}
0 & {-}1\\
1 & 0
\end{array}
\right]
$$ - 置き換えられた式を展開し、x, y 成分に分離された状態方程式に変換する。
(8)式の状態方程式の場合には次のようになります。
ただし、$r _x'{=}\Re({\boldsymbol{r}'})$, $r_y'{=}\Im({\boldsymbol{r}'})$, $v_x'{=}\Re({\boldsymbol{v}'})$, $v_y'{=}\Im({\boldsymbol{v}'})$,
$F _{rx}'{=}\Re({\boldsymbol{F}_r'})$, $F _{ry}'{=}\Im({\boldsymbol{F}_r'})$, $F _{sx}{=}\Re({\boldsymbol{F}_s})$, $F _{sy}{=}\Im({\boldsymbol{F}_s})$
$$
\begin{align}
&\frac{d}{dt}
\left[
\begin{array}{c}
r_x'\\
r_y'
\end{array}
\right]
=\left[
\begin{array}{c}
v_x'\\
v_y'
\end{array}
\right]\\[1ex]
&\frac{d}{dt}
\left[
\begin{array}{c}
v_x'\\
v_y'
\end{array}
\right]
=\frac{1}{m}
\left[
\begin{array}{cc}
\cos(-\omega t) & {-}\sin(-\omega t)\\
\sin(-\omega t) & \cos(-\omega t)
\end{array}
\right]
\left[
\begin{array}{c}
F_{sx}\\
F_{sy}
\end{array}
\right]\\[1ex]
&\hspace{5em}+\frac{1}{m}
\left[
\begin{array}{c}
F_{rx}'\\
F_{ry}'
\end{array}
\right]
-2\omega
\left[
\begin{array}{cc}
0 & {-}1\\
1 & 0
\end{array}
\right]
\left[
\begin{array}{c}
v_x'\\
v_y'
\end{array}
\right]
+\omega^2
\left[
\begin{array}{c}
r_x'\\
r_y'
\end{array}
\right]
\end{align}
$$
これらを一つにまとめると、次の(9)式のようになります。
$$
\begin{align}
\frac{d}{dt}
\left[
\begin{array}{c}
r_x'\\
r_y'\\
v_x'\\
v_y'
\end{array}
\right]
=&
\left[
\begin{array}{cccc}
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1\\
\omega^2 & 0 & 0 & 2\omega\\
0 & \omega^2 & -2\omega & 0
\end{array}
\right]
\left[
\begin{array}{c}
r_x'\\
r_y'\\
v_x'\\
v_y'
\end{array}
\right]\\[1ex]
&+
\left[
\begin{array}{cccc}
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0\\
1/m & 0 & \cos(\omega t)/m & \sin(\omega t)/m\\
0 & 1/m & -\sin(\omega t)/m & \cos(\omega t)/m
\end{array}
\right]
\left[
\begin{array}{c}
F_{rx}'\\
F_{ry}'\\
F_{sx}\\
F_{sy}
\end{array}
\right]\tag{9}
\end{align}
$$
(9)式の状態方程式を function 化したものと、これに対応する ode45 コマンドは次のようになります。
function dydt=rot_coord(t,y,Ww,Frx,Fry,Fsx,Fsy,Mm)
% y(1),y(2): 位置のx成分とy成分
% y(3),y(4): 速度のx成分とy成分
% Ww: 角速度、Frx,Fry: 回転座標の実在の力のx成分とy成分
% Mm: 質量、 Fsx,Fsy: 静止座標の実在の力のx成分とy成分
dydt = zeros(4,1); % dydt が列ベクトルであることを宣言
dydt(1) = y(3);
dydt(2) = y(4);
dydt(3) = Ww^2*y(1) + 2*Ww*y(4) + Frx/Mm + cos(Ww*t)*Fsx/Mm + sin(Ww*t)*Fsy/Mm;
dydt(4) = Ww^2*y(2) - 2*Ww*y(3) + Fry/Mm - sin(Ww*t)*Fsx/Mm + cos(Ww*t)*Fsy/Mm;
end
[t,y]=ode45(@(t,y) rot_coord(t,y,Ww,Frx,Fry,Fsx,Fsy,Mm), ...
[0:dT:Ts],[Rs0x Rs0y Vr0x Vr0y]);
% Rs0x,Rs0y: 初期位置のx成分とy成分
% Vr0x,Vr0y: 初期速度のx成分とy成分
蛇足: 図3のブロック線図の状態方程式((8)式)が、たまたま状態変数 $y_1$, $y_2$ に対して線形( $y_1$, $y_2$ の一次結合)だったため、実数化した最終的な状態方程式は、上の(9)式のような綺麗な線形形式( $d\boldsymbol{y}/dt{=}\boldsymbol{A}\boldsymbol{y}{+}\boldsymbol{B}\boldsymbol{u}$ )に纏まりました。しかし、一般にはすべての物理現象がこのような形に収まる訳ではありません。ただし、その場合でも、ode45 を使う上での障害になることはありません。一般化された(7)式の状態方程式の中の $f$ としては、$y_1y_2$、${y_1}^2$、$y_1t$、$\cos y_1$ などの非線形項を含むことも許されています。その場合には、(9)式のような線形形式にはなりませんが、$dy/dt=...$ として導出された式をそのまま記述するだけで大丈夫です。
(7)式の初出の段階では、$y$ として複素数も想定していたため、$y_1y_2$ のような項が存在すると困ることもあり、上記のコメントは明確に記述できませんでした。実数だけの状態方程式が現れたので、念のため、遅まきながら付け加えておきます。
上記の手順5と手順6で示した2種類のスクリプトにより、 素の MATLAB だけで 図3と図6の Simulink モデルと同一のシミュレーションを行い、その結果を図10に示しています。図5,7,8から、それぞれ代表的な1ケースずつを選んで計算した結果です。図5,7,8と同一の結果であることはもちろん、手順5の「複素数のままでルンゲクッタ」と、手順6の「実数だけに変換してルンゲクッタ」で、全く同一の結果が得られることも確認できました。複素数を選ぶのか、正攻法の実数で行くのか? はお好み次第です。

Simulink は、視覚的にシステムの検討を行う段階では非常に便利ですが、完成したシステムのシミュレーションを行うだけであれば、素の MATLAB でルンゲクッタ計算する方が処理時間は格段に短くなります。どちらを選ぶか、これもお好み次第です。
これで、素の MATLAB によるルンゲクッタ計算の要領はほぼ解説済みです。以降は Simulink によるシミュレーションだけに絞って話を進めることにします。
3.回転座標(フーコーの振り子)
前記事で提示した複素数形式の運動方程式について、これで妥当性の確認は一通り終わりました。ここからは、自然界の現象を対象にした応用編のシミュレーションに移ります。この記事で取り上げようとしている応用例では、我々が生活している地表面そのものを回転座標と見なします。そのため、まずは次の条件を受け入れることにします。
-
地球との接平面は その面内で $\pmb{\omega{=}\omega_e\sin\phi}$ で回転している。
ここで、地球は真球と仮定し、$\omega_e$: 地球の自転角速度[rad/s]、$\phi$: 地球と接平面との接点の緯度[rad](北緯が正) とします。以降、諸現象の観測はこの接点を中心にした比較的狭い領域で行われるものと考えます。なお、回転の中心は「接平面が地軸と交わる点」なので、そこから接点までの距離 $R$ は $|R_e/\tan\phi|$ となります( $R_e$: 地球の半径[m])。( 次項も含め、詳細については こちら(近日公開予定))。
-
水平面では、上記の回転による遠心力 $\pmb{m\omega^2R}$ は打ち消される。
地表上の森羅万象は、「地球による万有引力(中心に向かう力)」と「 $\omega_e$ による遠心力(地軸から遠ざかる力、最大でも引力の0.34%程度)」との合力を「重力」として感じています。しかし、個々の分力を識別することはできません。静止した振り子の糸の方向は「合力としての重力」の方向と一致し、水準器で体感できる水平面はそれと直角です。そのため、この水平面を「万有引力だけに直交する接平面」と比べると、僅かな角度($\pmb{\delta\hspace{0.1ex}\alpha}$)だけ南高北低(北半球)の坂になっています($\delta\hspace{0.05ex}\alpha{\simeq}0.092^{\circ}\text{@北緯}35^{\circ}$)。そして、この水平面が我々が生活している地表面になっています。
$\phantom{A}$
水平面に静かに置いた鋼球はどちらにも転がりませんから、「坂を転がり落とそうとする万有引力の地表北向きの分力 $mg\,\sin\delta\hspace{0.05ex}\alpha$」と「$\omega_e$ による遠心力 $m\omega_e^2R_e\cos\phi$ の地表南向きの分力 $m\omega^2\!R$」は大きさが同一で、互いに逆向きであることが分かります。したがって、接点においては、万有引力の地表方向の分力によって、$\pmb{m\omega^2R}$ で表される遠心力は打ち消されることになります。
一般に、振り子の初歩的な解析では、「振れ幅が十分に小さい」という仮定で近似計算が行われます。しかし、最初から近似に頼るのは、不都合なものは安易に無視してしまおうという悪い癖がつきそうで好きではありません。また、二次元解析しかできない複素数を使っていながら、三次元的な構造をイメージさせる振り子の動作を論じるのは気が引けます。
ということで、ここでは「振り子」とは言いながら「ばね+質量」で構成された水平面上の単振動系を考えることにします。この置き換えによる影響は、振動の周期が $2\pi\sqrt{重力加速度/糸の長さ}$ から $2\pi\sqrt{ばね定数/質量}$ に変わるだけです。置き換えを利用して説明をごまかそうと企んでいる訳ではありません。「理想的なバネ+質量系」であれば、振れ幅に制限はありません。また、緯度による重力加速度の微妙な違いによって振動の周期が変化することもありません。近似に頼らざるを得なくなる要因が大幅に減ります。
ところで、フーコーの振り子の振動の周期は、規模の大きなものでも十数秒です。しかし、この程度の短い周期でシミュレーションしたところで、振り子の軌跡として「塗り潰された部分円」が描かれるだけで面白くも何ともありません。そこで、ここでは周期2時間の特製の振り子を想定して検討することにします。もし、この仕様で現実の振り子を作ろうとすれば、糸の長さは、宇宙ステーションを遥かに超え、静止衛星の高度の1/3程度が必要になります。「ばね+質量」モデルにしても、輪ゴム1本でタイタニック号を引っ張るような型破りの条件になります。しかし、単なるシミュレーションですから、無謀な条件ではあっても何も怯む必要はありません。
なお、ここで想定する「ばね+質量」モデルは、バネの自然長が完全に0で、質点がバネの支点に衝突しそうになっても、そのまま素通りできるような、理想的で特別な仕組みが工夫されているものとします。
さて、以上を考慮して、既出の(4)式を変形していきます。
$$
\boldsymbol{F}'=\boldsymbol{F}_se^{-i\omega t}+\boldsymbol{F}'_r-i2m\omega\boldsymbol{v}'+m\omega^2\boldsymbol{r}'\tag{4再}
$$
まず、第1項の実在の力 $\boldsymbol{F}_s$ は $0$ とします。太陽からの引力とか地球の公転の遠心力とか、力としては色々と思い浮かびますが、それらはほぼキャンセルされるものとして大胆に無視します。近似や省略は好まないと言いながら、二枚舌で申し訳ありません。
第2項の実在の力 $\boldsymbol{F}'_r$ には、「質点を振動の中心に引き戻そうとするバネの力」と「万有引力の地表方向の成分 $mg\,\sin\delta\alpha$」があります。第3項、第4項は既に述べたコリオリの力と遠心力です。
ところで、(4)式が前提としている座標系は、その原点が「接平面の回転の中心」(遥か、北極の上空)にあり、実軸/虚軸は、接点(振り子の観測点)を通る東向き/北向きの線と平行です。しかし、これでは、原点が観測点からあまりにも離れ過ぎていて不便です。そこで、新しい原点が 接点の位置にくるように 座標を $\boldsymbol{R}_0$ だけ平行移動します。そして、新しい原点から見た質点の位置を暫定的に $\boldsymbol{r}''$ とおくと、$\boldsymbol{r}'{=}\boldsymbol{R}_0{+}\boldsymbol{r}''$ と表せます。また、バネの支点を 新しい原点に一致させると、質点を原点に引き戻す力は ${-}K\boldsymbol{r}''$ と表せます( $K$ : ばね定数 )。
以上に加え、$\boldsymbol{R}_0{=}{-}iR$ であること、万有引力の地表方向の分力は北向きなので虚数として $img\,\sin\delta\alpha$ と表されること、また、既述の遠心力の打ち消し条件により $mg\,\sin\delta\alpha{=}m\omega^2R$ であることなどを考慮すると、(4)式は次のように書き変えられます。(座標系を平行移動しただけなので、変化があるのは位置 $\boldsymbol{r}'$ だけです。速度 $\boldsymbol{v}'$ や力 $\boldsymbol{F}'$ の値は、どちらの座標系から見ても不変です)
$$
\begin{align}
\boldsymbol{F}'&=-K\boldsymbol{r}''+img\,\sin\delta\alpha-i2m\omega\boldsymbol{v}'+m\omega^2(\boldsymbol{R}_0+\boldsymbol{r}'')\\[1ex]
&=-K\boldsymbol{r}''+\cancel{img\,\sin\delta\alpha}-i2m\omega\boldsymbol{v}'-\cancel{im\omega^2R}+m\omega^2\boldsymbol{r}''\\[1ex]
&=-K\boldsymbol{r}''-i2m\omega\boldsymbol{v}'+m\omega^2\boldsymbol{r}''
\end{align}
$$
暫定的に導入した $\boldsymbol{r}''$ を 新しい回転座標系の変数 $\boldsymbol{r}'$ として読み替え、ブロック線図に適した形に変形すると次のようになります( $\boldsymbol{a'}{=}\boldsymbol{F}'/m$ )。
$$
\boldsymbol{a'}=-(K/m)\boldsymbol{r}'-i2\omega\boldsymbol{v}'+\omega^2\boldsymbol{r}'\tag{10}
$$
以上を考慮して、ブロック線図を図11のように描き変えました。「静止座標からの実在の力 $\boldsymbol{F}_s$ 」の経路は完全に削除して簡素化しました。新たには、$\omega{=}\omega_e\sin\phi$ の計算ブロックを追加しています。ここで、地球の回転周期が、振り子の振動周期(2時間)のちょうど整数倍の 24 時間となるような回転角速度 $\omega_e$ を設定しています。さらに、フーコーの振り子以外に、他の気象現象のシミュレーションとも共用できるように、図の右下に「質点を中心に引き戻そうとする力」の生成機能をいくつか作り込んでいます。1, 2, 3 のどれを選択するかは、SW_pos に設定する数値によって切替えます。フーコーの振り子では "1" を選択します。
他の用途と共用しているため、(10)式の $-(K/m)\boldsymbol{r}'$ の項に相当する部分のブロック線図が、なにやら持って回ったような表現になっていますが、じっくりと見れば動作は数式どおりです。K_Spring が $K$ に相当します。$K$ や質点の質量 Mass($m$)には、2 時間の振動周期を実現できる適正な値を設定しています。
なお、前例と同じく、回転座標から静止座標に変換するブロックを含んでいますが、ここに示す静止座標は便宜的なもので実体は曖昧です。単に、原点を新しい回転座標と共有して、相対的に ${-}\omega$ で回転しているというだけの座標です。しかし、この変換は、振り子の運動の本質を見極めるのには役立ちます。
その他、ゲインブロック Damping や 停止ブロック STOP は、フーコーの振り子のシミュレーションでは使わないので無効にしてあります。

蛇足:
フーコーの振り子を説明する多くの文献では、遠心力 $m\omega^2R$ を打ち消すのに合わせて、微少量であることを理由に (10)式の $\omega^2\boldsymbol{r}'$ に相当する項も無視してしまうのが普通です。その理由は、議論の目的がシミュレーションではなく、綺麗な近似式の導出にあるためと思われます。
しかし、式の形にまとめるときには障害になっても、数値解析でシミュレーションするだけであれば、この項が存在してもそれほど手間が増える訳ではありません。そこで、本記事では無視せずに進めることにします。無視した場合に現れる微妙な問題点についても後述します。
ただし、あとに続く気象現象のシミュレーションでは、$\omega^2\boldsymbol{r}'$ の項を残したままにしておくと、予想外の不満足な結果しか得られません。気象は広い面積にわたる現象であり、この全域を完全な平面であると考えるには無理があるためです。現実は球面であることを配慮しながら、うまく対処してやる必要があります。
図12、13にシミュレーション結果を示しています。図12は、中心から離れた位置(青〇印)で質点を解き放ったときの軌跡で、上半分は地表上で観測したもの、下半分は疑似的な静止座標から観測したものです。地表上では、半日(12時間)後には赤〇印まで移動し、それぞれの緯度 $\pmb{\phi}$ に応じて、180度$\pmb{\times\sin\phi}$ だけ回転していることが分かります。回転の原因がコリオリの力であることは、経路が右側へ微妙にカーブしていることから納得できます。静止座標上では、周期ごとの軌跡は同一ですが、緯度に応じて楕円の形状が変わります。楕円になるのは、質点を静かに手放したつもりでも、地表の回転方向に、意図しない初期速度が与えられるためです。
一般には上のような初期条件でシミュレーションされることが多いのですが、稀に、これとは異なる条件で行われることもあります。例えば、図13は、質点を中心位置から射出した場合の軌跡です。射出の初期速度は、振れ幅を図12と合わせるように設定しています。軌跡の形状はかなり異なりますが、12時間で回転する角度は図12と同じです。始点と終点が重なっているので、回転角度の正確な読み取りは容易ではありませんが、北緯10度や30度あたりの軌跡で比べてみれば納得できます。静止座標上の軌跡が直線になるのは、質点が中心から出発しているため、回転方向の初期速度が存在しないためです。


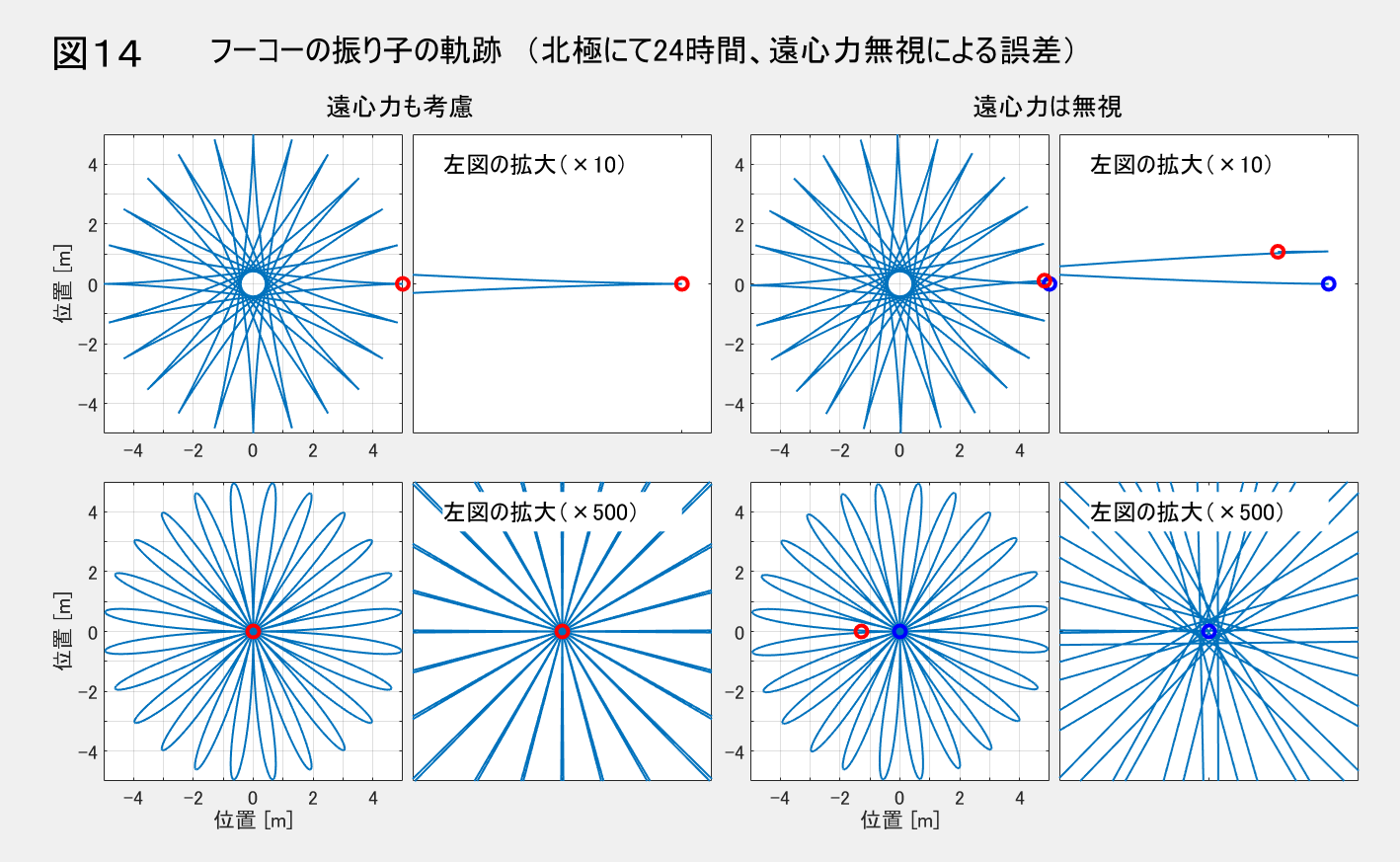
以上は、(10)式の第3項(キャンセルされずに残った遠心力の微小項 $\omega^2\boldsymbol{r}'$ )まで考慮した軌跡です。一方、これを無視した場合との差異を示したのが図14です。違いが分かりやすいよう、北極(北緯90度)において 24 時間にわたって振らせる条件にしています。左半分は遠心力を考慮したとき、右半分は無視したときです。考慮している場合には、始点の青〇印の上に終点の赤〇印がピッタリと重なって、正確に元の位置に戻っています。しかし、無視した場合には若干のズレが生じています。やはり、正確なシミュレーションのためには、残存遠心力を無視すべきではないことが分かります。
4.回転座標(傾度風)
つぎは、これまた、コリオリの力が大活躍する気象現象のシミュレーションに移ります。ブロック線図は前掲の図11を、一部の設定を変更して流用します。
これまでは、できるだけ近似を避けるように留意してきましたが、ここからは近似だらけの大胆な手法に切り替わります。気象現象は、本来は流体力学や熱力学などの難しい理論も駆使し、精密にシミュレーションすべきものでしょうが、ここでは一塊の空気を一つの質点に置き換えるだけという乱暴な近似で済ませてしまいます。精度は推して知るべしです。しかし、気象現象をこのような近似で説明している資料は多くみられるので、ある程度は認知されている方法と思われます。
以上も含めて、ここでのシミュレーションの条件は下記の通りとします。
-
まずは、任意の位置にある 1×1×1 [m] の立方体内の空気を一つの質点に置き換えます。体積は一定でも気圧や温度によって質量は変わりますが、基準状態(0℃,1気圧,湿度0%)での質量が常に一定に保たれるものとします。$m=1.29\ \text{[kg]}$
-
この質点に作用する力は、その立方体の対向する面と面との間の気圧の差になります。言い換えれば、その点の気圧傾度[Pa/m]( [N/m$^\mathbf{3}$] )が質点に作用する力になります(気圧傾度力)。普通の天気図の等圧線は 4 [hPa] ごとに引かれているので、等圧線の間隔が $L$ [km] のときの気圧傾度力 $F'_p$ [N] は、
$F'_p=4{\times}100/(1000{\times}L)=0.4/L$
北海道の端から九州の端までを約 2000 [km] とすれば、この間に4本程度の等圧線があるときの気圧配置では、$L{=}400$ [km] として $F'_p{=}0.4/400{=}0.001$ [N] (≒0.1g重)となります。
-
地球の自転による遠心力は完全に無視します。フーコーの振り子の場合には、非常に狭い理想平面内で議論するだけで済みました。しかし、気象現象は広範囲に渡るので、地表が球面であることは無視できません。どの地点においても、そこが地球との接点を持つ微小水平面であると考えれば、検討する全領域内で、遠心力は完全に打ち消されます。
-
すべての地点が地球との接点であると解釈すれば、その地点の緯度に応じて、回転座標の角速度はまちまちになります。しかし、そこまでは考えません。検討する領域の中央あたりの角速度で、全域が一様に回転しているものとします。
以上をふまえて傾度風のシミュレーションを行います。傾度風とは、等圧線がカーブしているときに、地表との摩擦が少ない上空で、等圧線に沿って吹く風のことを言います。質点が気圧傾度力だけで運動するのであれば、低気圧の中心に向かい、あるいは、高気圧の中心から、中心線に沿って直線的に移動するだけです。しかし、その他の力も作用するので、これとは直角方向に円を描いて移動するようになります。この風の風速は、等圧線の間隔や曲率によって決まります。具体的には、気圧傾度力・コリオリの力・遠心力がつり合う速度になります。
遠心力については、上記で「完全に無視」と宣言しながら、ここでまた現れることに違和感があるかもしれません。しかし、この新たな遠心力を生じさせる回転座標は、$\omega_e\sin\phi$ で回転する既出の第一の回転座標とは別物です。第一の回転座標のさらにその上で、傾度風と同期した相対的な角速度 $\omega'$ で回る第二の回転座標です。この座標とともに回転しながら現象を観測するときには、ここで生じる遠心力まで無視してしまうことはできません。この座標の相対角速度 $\omega'$ は、傾度風の曲率半径を $r'$、風速を $v'$ とすれば、$\omega'{=}v'/r'$ となります。なお、第二の回転座標から見た質点は、座標の回転と同期して静止状態にありますから、$\omega'$ によるコリオリの力は生じません。コリオリの力は $\omega$ によるものだけになります。
ここでは、同心円状に等間隔の等圧線が描かれている天気図をモデルにします。上記の3つの力はすべて、円の中心と質点とを結ぶ同一の直線上にあるため、つり合いの数式はスカラー量だけで表せて次のようになります。左辺の第1項は気圧傾度力、第2項はコリオリの力(他の力と同一方向なので虚数単位 $i$ は不要です)、第3項は遠心力です。ただし、力の正方向は円の中心から質点に向かう向き、風速 $v'$ の正方向は反時計回り、気圧傾度力 $F'_p$ の符号は、高気圧のときは正、低気圧のときは負となります。
$$F'_p+2m\omega v'+mr'\omega'^2=F'_p+2m\omega v'+\frac{mv'^2}{r'}=0$$
この二次式方程式を風速 $v'$ について解くと、次のようになります。
$$v'=-r'\omega\pm\sqrt{r'^2\omega^2-\frac{r'F'_p}{m}}$$
この式に、既述の $m$ の値や北緯 38 度における回転座標の角速度 $\omega$ の値を代入し、$r'$ と $|v'|$ の関係をグラフ化したものが図15です($\pm$ の符号については、常識的な風速を示す方だけを採用しています)。

この図より、気圧傾度が 0.001[Pa/m] のとき、気圧の中心から 600[km] の地点では、低気圧で 7.6[m/s]、高気圧で 10.9[m/s] が傾度風の風速になることが分かります。この風速のときには、風の経路が等圧線に沿った形になることをシミュレーションによって確認してみます。図11において、切替スイッチ指令 SW_pos は "2"、遠心力は完全に無視するので、ゲイン Cf は "0"、質点の質量 $m$ (Mass) は 1.29[kg]、緯度は 38 度、初期位置 $r'_0$ (init_Position) は "600e3" のように変更し、初期速度 $v'_0$ (init_Velocity) や気圧傾度力 Grad_Forceはその都度、必要な値に設定します。
ここで、「傾度風と同期して回る第二の回転座標と、これによる遠心力を模擬するブロックはどこにあるんだ?」という疑問が湧くかもしれません。しかし、図11のシミュレーションは、あくまで地球の自転に由来する第一の回転座標上だけで行っているものです。便宜的に導入したその他の回転座標上の見掛けの力が入り込む余地はありません。余計なブロックを追加しなくても正しい結果が得られます。
シミュレーション結果は図16のようになります。赤色の線が傾度風の経路で、等圧線に沿った円になることが確認できました。青色の線と緑色の線は、それぞれ、傾度風の約半分と2倍の風速を与えたときの経路です。しかし、実際にはこのような経路の風は存在しないようです(もしかすると、偏西風の蛇行を示唆??)。どのような初期風速であろうとも、それなりの円形経路に収束する過程を示してこそのシミュレーションなのでしょうが、簡略法の限界はここまでです。申し訳ありません。

5.回転座標(台風の渦)
次は、台風のシミュレーションです。傾度風のグラフからも分かるように、気圧傾度が一様な低気圧だけでは、中心部の風速が大きい台風のような現象は起きません。しかし、ここで行う簡略シミュレーションでは、台風の気圧配置が自動生成されるような高度なことはできません。そこで、少々手抜きをして、実測から割り出された既成の気圧分布の式を利用します。下記は「藤田の式」と呼ばれる台風の気圧分布を示す式です。ただし、$P_\infty$ : 周辺部の気圧、$P_0$ : 中心気圧、$\Delta P$ : 気圧差 $(P_\infty{-}P_0)$、$r$ : 中心からの距離、$r_m$ : 分布型を決める定数。
$$P(r)=P_\infty-\frac{\Delta P}{\sqrt{1+\left(\frac{r}{r_m}\right)^2}}$$
ここで、$P_\infty{=}1013$ [hPa]、$P_0{=}940$ [hPa]($\Delta P{=}73$ [hPa])、$r_m{=}80$ [km] として、上式が表す気圧分布のグラフと等圧線の配置のイメージを示すと図17のようになります。足切り無しの気圧分布のグラフを見ると、この程度の気圧の不均衡であのような強風が吹くことに驚きます。

この気圧分布の式を $r$ で微分すると、気圧傾度力 $F_p$ は次のように求まります。
$$F_p=\frac{dP(r)}{dr}=\frac{r\Delta P}{{r_m}^2\sqrt{1+\left(\frac{r}{r_m}\right)^2}^3}$$
図11の切替スイッチ指令 SW_pos を "3" として、 MATLAB Function ブロックの Fujita には上式を次のように埋め込みます。
function Fp = Fujita(dP,Rm,Ra)
Fp=Ra*dP/(Rm^2*(1+(Ra/Rm)^2)^(3/2));
このブロックへの入力となる台風の気圧差 $\Delta P$ (dP) は 73e2、分布型の定数 $r_m$ (Rm) は 80e3 に設定します。今回は渦巻を生じさせるために、若干の抵抗を加えてゲイン Damping を 10e-6 とします。傾度風のときと同様、遠心力は完全に無視するので、ゲイン cf は 0 のままです。また、このケースでは適切なシミュレーション時間の見積もりは困難なため、長めの設定にしておき、中心から 4 [km] の地点まで近づいたら実行を中断させることにします(定数ブロック Rs を 4e3 に設定)。この処理は、次のような機能を埋め込んだ MATLAB Function ブロック Judge により行います。
function Stp = Judge(Rs,Ra)
if Rs==0; Stp=false;
elseif Ra<Rs; Stp=true;
else; Stp=false;
end
以上の条件において、北緯 30 度でシミュレーションした結果を図18に示します。適当な遠方から初速 0 でスタートさせていますが、その地点の気圧傾度に適合した速度ではないため、最初は振動ぎみになります。しかし、ダンピングが効いているため、暫くすれば安定した渦状の軌跡に落ち着きます。また、最大風速はそこそこ尤もらしい値になり、台風の目に入れば風はピタリと止みます。一部の設定項目は、それらしい結果が得られるように適当に入力しており、その値には確たる根拠はありません。図示はしていませんが、ゲイン Damping を増/減すると、渦を巻く回数は減/増するものの、意外なことに最大風速は殆ど変化しません。

以上、検討対象の全領域において回転座標の角速度が均一であると仮定したシミュレーションでした。しかし、緯度に応じて角速度を変化させれば、さらに現実に近い興味深い結果が得られるのではないか? という思いが残ります。そこで、図11の定数ブロック Latitude(北緯の度) と乗算ブロックの間に、下記のスクリプトを持つ MATLAB Function ブロックを追加して再度シミュレーションしてみました。入力 lat0 は検討対象領域の中心部の緯度、出力 lat は質点が存在する地点の緯度です。中心部からの距離 R(複素数)には信号 $r'$ を引き込みます。
function lat = Latitude(R,lat0)
Re=6371; R=R/1000;
c=abs(R)/Re;
alpha=pi/2-angle(R);
lat1=lat0*pi/180;
lat2=asin(sin(lat1)*cos(c)+cos(lat1)*cos(alpha)*sin(c));
lat=lat2*180/pi;
シミュレーション結果の図は割愛しますが、軌跡や風速のグラフに若干の変化は見られたものの、残念ながら、新しい知見が得られるような顕著な見どころはありませんでした。
6.惑星の運動(保存量不使用)
前記事では最終的に、複素座標の原点を太陽に置き、惑星が動径と直角方向に運行するタイミングを $t{=}0$ として、そのときの動径を実軸に選ぶことにしました。また、惑星の位置を $\boldsymbol{r}{=}re^{i\theta}$ とすれば、惑星に働く力 $\boldsymbol{F}_g$ は次式の第2辺で表されることを示しました(前記事の(9)式)。これを $\boldsymbol{r}$ の関数となるように変形すれば、第3辺が得られます。ただし、$G$ は万有引力定数 6.67e-11 [N m$^2$ kg$^{{-}2}$]、$M$ は太陽の質量 1.99e30 [kg]、$m$ は惑星の質量です。
$$
\boldsymbol{F}_g=-\frac{GMm}{r^2}e^{i\theta}=-\frac{GMm}{|{\boldsymbol{r}}|^2}e^{i\arg{\boldsymbol{r}}}
$$
これにニュートン力学の第2法則 $\boldsymbol{F}_g{=}m(d^2\boldsymbol{r}{/}dt^2){=}m(d\boldsymbol{v}{/}dt)$ を適用し、Simulink と対応づける既述の手順に従えば次の式が得られます。
$$
\begin{align}
&\boldsymbol{v}=\color{#bbb}{\int_0^t\frac{\boldsymbol{F}_g}{m}dt+\boldsymbol{v}_0}=-\int_0^t\frac{GM}{|{\boldsymbol{r}}|^2}e^{i\arg{\boldsymbol{r}}}dt+\boldsymbol{v}_0\\
&\boldsymbol{r}=\int_0^t\boldsymbol{v}\,dt+\boldsymbol{r}_0
\end{align}
$$
これをブロック線図として表すと図19のようになります。回転座標系のブロック線図に比べるとかなりシンプルです。身近にあるフーコーの振り子よりも、神秘的な大宇宙の天体の運行の方が より単純な物理現象だというのはなかなか信じられません。
ここで新たに現れた MATLAB Function ブロック Fstp は、惑星が太陽から離れ過ぎてグラフ面内には戻ってきそうもないことを悟ったとき、シミュレーションを停止させるように導入したものです。とは言っても、高度で複雑な判断をしている訳ではなく、次のように単純な内容です。これだけでも、ブロックの組み合わせだけで実現しようとすると かなりのスペースを必要とします。
function Stp = Pstp(Ra)
Stp=abs(imag(Ra))>=30;
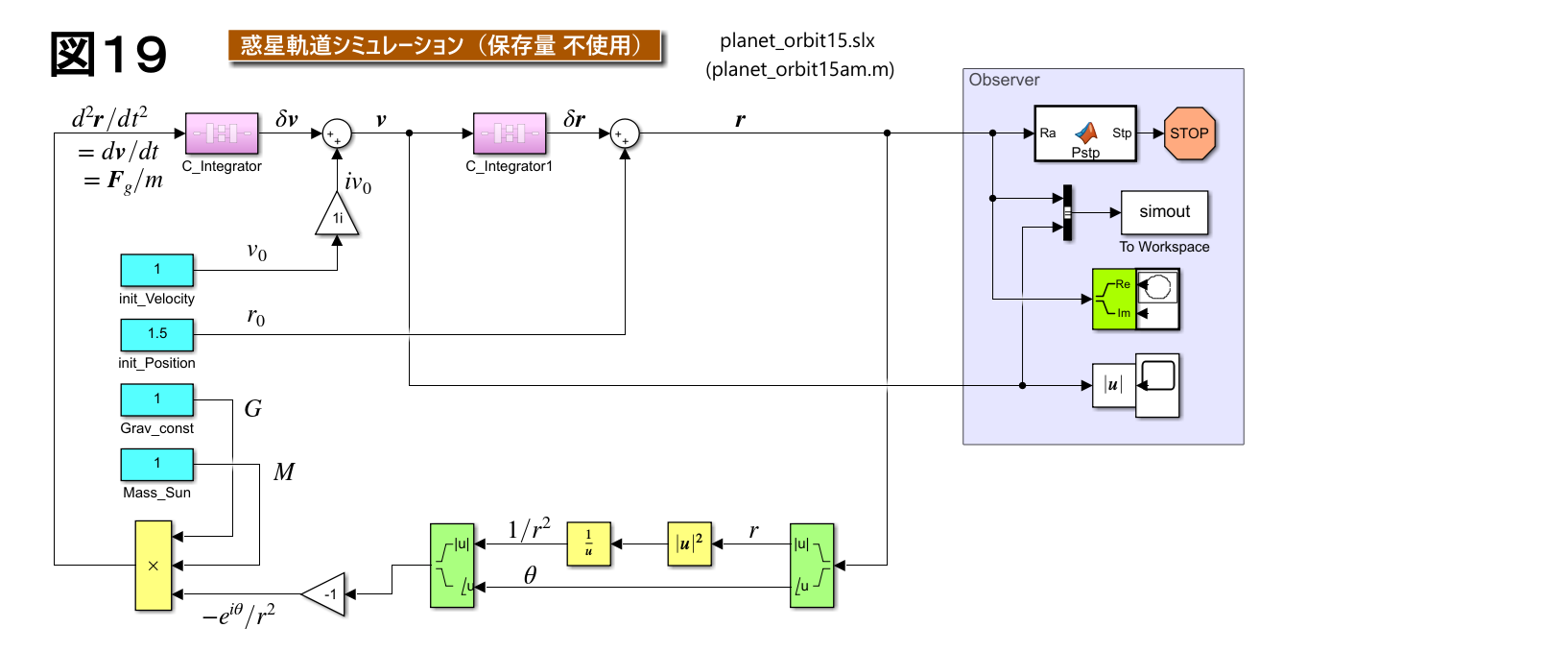
なお、このブロック線図では、$\pmb{G}$, $\pmb{M}$, $\pmb{v_0}$, $\pmb{r_0}$ の値として、真値ではない適当な値を設定しています。しかし、「話が何となく杜撰になってきた」などと思われないよう、理由を簡単に説明しておきます。今までの例では、できるだけ身の回りのスケールに合うような数値を使用してきました(レコードプレーヤーのターンテーブル、回転する陸上競技場、日本周辺の地図など)。しかし、ここからはスケールが段違いです。$G$ や $M$ などは、10$^{{-}11}$ や 10$^{30}$ という想像できないレベルの超微小数、超巨大数です。そのまま使用しても直感的に理解できる訳でもなく、かえって分かりにくくなります。
現在では MATLAB の基本仕様のままでも、浮動小数の 10 進 16 桁で、ほぼ 10$^{{-}300}$ ~ 10$^{300}$ の範囲の数値が扱えます。ダイナミックレンジが途方もなく広くなっています。したがって、$G$ や $M$ は、当然そのままの値でも使おうと思えば問題なく使用できます。
ところがアナログコンピュータの時代には、すべての状態変数は、感電しない程度のアナログ電圧の正負の領域に収めなければなりません。その出力電圧波形を記録する装置の分解能や即応性もそれほど高くはありません。総合的にダイナミックレンジが極端に狭かったのです。これに伴って、定数の値も真値をそのまま使用するのは困難になります。そのため、スケーリングという作業が必ず必要になります。演算増幅器の出力電圧範囲を最大限に有効利用して、解析しようとしているモデルの距離〇[m]を電圧◇[V]に、速度△[m/s]を電圧▽[V]に対応させようという見積もり作業です。対応の比率は自由に決められる訳ではなく、最終的には全体の辻褄が合うような帳尻合わせも必要でした。「この IT 時代に、なぜ前世紀の苦労話など聞かなければならないのだ。老害もいいところだ。」とお思いでしょう。しかし、真の値をそのまま使用しないテクニックも知っておいて損はありません。思いがけない所で役立つはずです。
次元解析の教えによれば、電気系を含まない物理現象では、長さL, 質量M, 時間T の3つの次元の組み合わせだけですべての単位を表現できるとされています。例えば、力の単位 [N] は、$\boldsymbol{F}$[N] $=m$[kg] $\boldsymbol{a}$[m/s$^2$] であることを考えれば [kg m /s$^2$] と表現することができます。したがって、万有引力定数の単位 [N m$^2$/kg$^2$] は [m$^3$/( kg s$^2)$] となります。
また、"=" で関係付けられる量の両辺の単位が同一であれば、数値も同一にならなければなりません。L, M, T の MKS 単位系での標準単位は m, kg, s です。ここでは対応づけに手間どる L, M, T というシンボル名は使わずに、自分に都合の良い数値に読み替えるための「俺さま単位系」として mo, kgo, so を導入することにします(標準単位の後に oresama の"o"を付けた、ここだけでの我流表現です)。
図19では、万有引力定数 $G$ [m$^3$/( kg s$^2)$] や太陽質量 $M$ [kg] という明確な値を、ただ単に 1 と置いてしまっています。また、長さや時間の具体的な数値はまだ決めていませんが、とりあえずこれを $r_u$ や $t_u$ と置けば次のような関係式が成り立ちます。
$$
\begin{align}
&1\ [\mathsf{mo}] = r_u\ [\text{m}]\\
&1\ [\mathsf{kgo}] = M\ [\text{kg}]\\
&1\ [\mathsf{so}] = t_u\ [\text{s}]\\
&1\ [\mathsf{mo}^3/( \mathsf{kgo}\ \mathsf{so}^2)] = G\ [\text{m}^3/( \text{kg}\ \text{s}^2)]
\end{align}
$$
上の 4 番目の式の右辺を、左辺と同一の単位系となるように変形すると次のようになります。
$$
\begin{align}
1\ [\mathsf{mo}^3/( \mathsf{kgo}\ \mathsf{so}^2)]
&=G\ [\text{m}^3/( \text{kg}\ \text{s}^2)]=
G\left[\frac{(\frac{1}{r_u}[\mathsf{mo}])^3}{\frac{1}{M}[\mathsf{kgo}] (\frac{1}{t_u}[\mathsf{so}])^2}\right]\\
&=\frac{GM{t_u}^2}{{r_u}^3}[\mathsf{mo}^3/( \mathsf{kgo}\ \mathsf{so}^2)]
\end{align}
$$
したがって、定数を適当に設定したシミュレーションではありますが、その結果を解釈するときに $\pmb{GM{t_u}^2{=}{r_u}^3}$ の関係が保たれるように配慮すれば、辻褄が合った正しい答えが得られます。
これを前提として、図19のブロック線図によるシミュレーション結果を次に示しています。図20は、実軸上の初期位置 $\boldsymbol{r}_0$ を一定値 $1.0$ としたまま、初期速度 $\boldsymbol{v}_0$ を虚軸方向に各種変化させたときの惑星の軌跡、図21は、逆に、初期速度 $\boldsymbol{v}_0$ を一定値 $1.0\,i$ としたまま $\boldsymbol{r}_0$ を変化させたときの軌跡です。図中に単位は明示していませんが全て俺さま単位です。
軌跡のみでは惑星位置の時間的変化が分かり難いので、一つの代表的な楕円軌道上に、等時間間隔の〇印で位置を示しています。これらの時間間隔は、$\varepsilon{=}1$ の惑星が真円軌道を1周する時間と同じです。細い破線は、万有引力定数が負だった場合の仮想的な軌跡です。興味本位で描いてみました。


図22には、図21上のすべての楕円軌道について、動径の角度 $\theta$ を横軸にして、太陽からの距離 $|\boldsymbol{r}|$、惑星の速度の絶対値 $|\boldsymbol{v}|$ とその $\theta$ 方向成分 $v_{\theta}$、スタート点からの経過時間の変化を縦軸に示しています。しかし、俺さま単位系のままでは現実世界との対応づけが困難なので、ここで、$1\ [\mathsf{mo}]{=}r_u\ [\text{m}]$ の $r_u$ を太陽と地球間の平均距離 1.5e11 [m] に選びます。すると、$GM{t_u}^2{=}{r_u}^3$ の関係より、$1\ [\mathsf{so}]{=}t_u\ [\text{s}]$ の $t_u$ の値は一意的に定まり次のようになります。
$$
t_u=\sqrt{\frac{r^3}{GM}}=\sqrt{\frac{(1.5{\times}10^{11})^3}{6.67{\times}10^{-11}{\times}1.99{\times}10^{30}}}=5.043{\times}10^6\ [\text{s}]
$$
また、速度 $1\ [\mathsf{mo}/\mathsf{so}]$ の実値は次のとおりです。
$$
1\ \left[\frac{\mathsf{mo}}{\mathsf{so}}\right]=1\ \left[\frac{r_u [\text{m}]}{t_u [\text{s}]}\right]=\frac{r_u}{t_u}[\text{m/s}]=\frac{1.5{\times}10^{11}}{5.043{\times}10^6}=2.974{\times}10^4[\text{m/s}]
$$
これは一般に言われている地球の公転速度 29.8 [km/s] とほぼ同じです。また、下図に示している $r_0{=}1.0$ での回転周期 6.2832 $[\mathsf{so}]$ の実値は、$6.283\,t_u$${=}$$6.283{\times}5.043{\times}10^6$${=}$$31.69{\times}10^6[\text{s}]$${=}$$367[\text{day}]$ で、ほぼ一年です。以上の要領で実値との対応づけを行えば、その他の具体的な事象についても実値での特性を知ることができます。

6.惑星の運動(保存量利用)
さて、前記事では、惑星軌道についての説明の中心は保存量の導出にありました。ここで導出した保存量は軌道形状の解析に大いに役立ちました。そこで、この保存量を利用すれば、もっと効率的なシミュレーションができるのではないか? という期待が膨らんできます。この観点から、保存量を利用したブロック線図も作ってみることにします。前記事で現れた保存量は次の2つです。ただし、$L$ : 角運動量、$\varepsilon$ : 離心率、$r$ : $|\boldsymbol{r}|$、$v$ : $|\boldsymbol{v}|$、$\varphi$ : $\boldsymbol{v}$ と $\boldsymbol{r}$ の角度差、$\dot\theta$ : $d\theta/dt$。
$$
L=mr^2\dot{\theta}=mrv\sin{\varphi}
$$
$$
\varepsilon=-i\frac{L}{GMm}\boldsymbol{v}-e^{i\theta}
$$
軌道上の一点における保存量 $L$ や $\varepsilon$ の値が分かれば、同一軌道の他の位置においてもそれらの値は変わりません。図19のブロック線図では、$G$, $M$ が既知であり、さらに、$t{=}0$ における角度 $\theta$, $\varphi$ は 0°, 90°、初期速度と位置は $v_0$ と $r_0$ で与えられていますから $L$ や $\varepsilon$ は次のように決まります。
$$
L=mr_0v_0\sin(\pi/2)=mr_0v_0
$$
$$
\varepsilon=-i\frac{mr_0v_0}{GMm}iv_0-e^0=\frac{r_0{v_0}^2}{GM}-1
$$
$L$ が既知なので、$\boldsymbol{v}$ から次のようにして $r$ と $\dot\theta$ が求まります。ただし、$\theta$ も既知である必要があります。$\dot\theta$ が未知なのに $\theta$ を既知と考えることには少々抵抗がありますが、$\theta$ の値は前ステップ時の積分値として残っていると考えればある程度は納得できます。
$$
\begin{align}
&r^2\dot\theta=L/m=mr_0v_0/m=r_0v_0\\[1ex]
&r\dot\theta=v_\theta=|\boldsymbol{v}|\sin\varphi=|\boldsymbol{v}|\sin(\arg \frac{\boldsymbol{v}}{\boldsymbol{r}})=|\boldsymbol{v}|\sin(\arg \frac{\boldsymbol{v}}{e^{i\theta}})\\[1ex]
&\hspace{1em}=\Im(|\boldsymbol{v}|e^{i(\arg\boldsymbol{v}-\theta)})=\Im(|\boldsymbol{v}|e^{i\arg\boldsymbol{v}}/e^{i\theta})=\Im(\boldsymbol{v}/e^{i\theta})\\[1ex]
&r=r^2\dot\theta/r\dot\theta\\[1ex]
&\dot\theta=r\dot\theta/r
\end{align}
$$
また、$\varepsilon$ の定義式から $\boldsymbol{v}$ が次のように求まります。
$$
\boldsymbol{v}=i\frac{GMm}{L}(\varepsilon+e^{i\theta})=i\frac{GM}{r_0v_0}(\varepsilon+e^{i\theta})
$$
これらを利用してブロック線図を作り直したものが次の3つの図です。なお、図19で薄紫色の背景内に示している観測系のブロック類のグループは、ここではサブシステム化して小さく圧縮しています。図23は、2つの保存量 $L$, $\varepsilon$ のうち $L$ だけを利用、図24は $\varepsilon$ だけを利用、図25は $L$, $\varepsilon$ の両方を利用したものです。



3種類のどのブロック線図も、図19と入れ替えてシミュレーションすれば、図20~22と全く同一の結果が得られます。しかし、どのブロック線図も 保存量不使用の図19よりも複雑になっており、シミュレーションを効率化しようとする目論見は外れてしまったという残念感があります。確かに、普通にシミュレーションするだけであれば図19だけで十分です。
しかし、せっかく作ったブロック線図なので、何か一つでも利点を示したいものです。その気になって眺めると、図19, 23, 24, 25と進むにつれて積分器の数が4、3、2、1個と減っていくのに気付きます(1つの複素数積分ブロックは普通の積分器の2つ分と数えます)。ということは、微分方程式が解きやすくなっているはずです。
今までは「可変ステップ」で指定してきたソルバーを、「固定ステップ」の「ode4」に変更して、各種のサンプル時間(時間刻み)でシミュレーションした結果を図26に示します(固定ステップソルバは MATLAB 本体には装備されておらず、Simulink だけで使用できる機能です)。図21の中で最も内側にある2種類の楕円についてシミュレーションしています(なぜか発散しやすい条件なので)。やはり、保存量を利用するほど(積分器を減らすほど)安定したシミュレーションができていることが分かりました。めでたし、めでたし。

7.ラザフォード散乱
図20, 21では、本来はあり得ない負の引力まで想定して、そのときの軌道を遠慮ぎみに披露しました。しかし、ここからは斥力の本当の出番になります。正の電荷どうしを衝突させようとするシミュレーションなので、引力ではなく、間違いなく斥力が働きます。ラザフォードは、金箔にアルファ線(ヘリウムの原子核)を照射すると、その一部が手前にも弾かれることを発見し、原子の構造の解明に貢献しました。原子は正負の電荷が溶け合ったような構造ではなく、中心に小さな正の電荷があり、負の電荷がその周りを希薄に取り巻いているという重要な発見です。
正の電荷どうしに働く力 $\boldsymbol{F}_e$ は次の1行目の式で表されます。これを2行目の万有引力による力 $\boldsymbol{F}_g$ と比較してみると、$GM\Leftrightarrow{-}Qq/4\pi\epsilon_0m$ なる対応があることが分かります。ただし、$Q$ : 金の原子核の電荷、$q$ : ヘリウム原子核の電荷、$m$ : 質点(今はヘリウム原子核)の質量、$\varepsilon_0$ : 真空の誘電率 です。
$$
\begin{align}
&\boldsymbol{F}_e=\frac{Qq}{4\pi\varepsilon_0r^2}e^{i\theta}=\frac{Qq/m}{4\pi\varepsilon_0}\cdot\frac{m}{r^2}e^{i\theta}\\[1ex]
&\boldsymbol{F}_g=-\frac{GMm}{r^2}e^{i\theta}
\end{align}
$$
上の $GM$ 相当量を、陽子1個の電荷 $e_p$ や質量 $m_p$ を使って変形すると、金 $\sideset{ _{\hspace{1ex}79}^{197}}{}{\mathrm{Au}}$ とヘリウム $\sideset{ _{2}^{4}}{}{\mathrm{He}}$ の場合には次のようになります。
$$
-\frac{Qq}{4\pi\varepsilon_0m}=-\frac{79e_p\cdot 2e_p}{4\pi\varepsilon_0\cdot 4m_p}=-3.143\frac{{e_p}^2}{\varepsilon_0m_p}
$$
ここでもまた、理科年表を見なければ分からないような複雑で超微小な数値( $\varepsilon_0$, $e_p$, $m_p$ )は、すべて俺さま単位の 1 に置き替えると、$GM$ 相当量は -3.143 になります。したがって、 ラザフォード散乱のシミュレーションも、$G{=}{-}3.143$, $M{=}1$ と置いて図19のブロッック線図がそのまま流用できます。図27には、これに沿ってシミュレーションしたアルファ線の軌跡を示しています。金箔に向けて右からアルファ線を照射したときの散乱の様子が綺麗に再現できています。

アルファ線の照射位置の実軸からの距離 $b$ と、散乱による偏向角度 $\varTheta$ との間には次の関係があることが知られています。ただし、$v$ : 照射速度。
$$
b=\frac{Qq}{4\pi\varepsilon_0mv^2}\cdot\frac{1}{\tan(\varTheta/2)}
$$
既述の $GM$ 相当量の計算結果を適用すると、$b=3.143/{v^2\tan(\varTheta/2)}$ となります。シミュレーションでは照射速度 $v_0$ は 7 と置いていますから、$\varTheta$ が 90°( $\tan(\varTheta/2){=}1$ )となるときの $b$ は $3.143/7^2$${=}0.0641$ となります。これは、図中の $r_0{=}10\pm0.0641i$ の水色の線に相当し、シミュレーション結果が正しいことが確認できます。
さて、ここでも、俺さま単位を使った後始末として、最後に辻褄合わせをやっておきます。なお、電気的な現象を含む場合には、基本単位は MKS だけでなく A(アンペア)も必要になります。既に述べたように $m_p$, $e_p$, $\varepsilon_0$ は 1 と置いたので、次の 1~3 行目の関係が成り立たなければなりません。また、距離と時間については 4, 5 行目の関係があるものとします。
$$
\begin{align}
&1\ [\mathsf{kgo}] = m_p\ [\text{kg}]\\
&1\ [\mathsf{so}\ \mathsf{Ao}] = e_p\ [\text{s}\ \text{A}]\\
&1\ [\mathsf{mo}^{\text{-}3}\ \mathsf{kgo}^{\text{-}1}\ \mathsf{so}^4\ \mathsf{Ao}^2] = \varepsilon_0\ [\text{m}^{\text{-}3}\ \text{kg}^{\text{-}1}\ \text{s}^4\ \text{A}^2)]\\
&1\ [\mathsf{mo}] = r_u\ [\text{m}]\\
&1\ [\mathsf{so}] = t_u\ [\text{s}]\\
\end{align}
$$
ここでは、電流の次元は最終的にはキャンセルされるので、小賢しいことは考えずに $[\mathsf{Ao}]{=}[\text{A}]$ としておきます。すると、2 行目と 5 行目の式より次のようになり、$t_u{=}e_p$ が成り立つ必要があることが分かります。
$$
1\ [\mathsf{so}\ \mathsf{Ao}] = e_p\ [\text{s}\ \text{A}] = e_p\ [\frac{1}{t_u}\mathsf{so}\ \mathsf{Ao}] = \frac{e_p}{t_u}\ [\mathsf{so}\ \mathsf{Ao}]
$$
さらに、3 行目の式を変形すると、
$$
\begin{align}
&1\ [\mathsf{mo}^{\text{-}3}\ \mathsf{kgo}^{\text{-}1}\ \mathsf{so}^4\ \mathsf{Ao}^2] = \varepsilon_0\ [\text{m}^{\text{-}3}\ \text{kg}^{\text{-}1}\ \text{s}^4\ \text{A}^2)]\\[1ex]
&=\varepsilon_0\ \left[\left(\frac{1}{r_u}[\mathsf{mo}]\right)^{\text{-}3}\ \left(\frac{1}{m_p}[\mathsf{kgo}]\right)^{\text{-}1}\ \left(\frac{1}{t_u}[\mathsf{so}]\right)^4\ \mathsf{Ao}^2\right]\\[1ex]
&=\frac{\varepsilon_0\,{r_u}^3\,m_p}{{t_u}^4} [\mathsf{mo}^{\text{-}3}\ \mathsf{kgo}^{\text{-}1}\ \mathsf{so}^4\ \mathsf{Ao}^2]
\end{align}
$$
これにより、$\varepsilon_0\,{r_u}^3\,m_p{=}{t_u}^4{=}{e_p}^4$ が成り立つことが要請されるので、グラフ上の 1.0 の長さの実値 $r_u$ は次のようになります。
$$
\begin{align}
r_u&=\sqrt[{\Large 3}\leftroot{4}\uproot{2}]{\frac{{e_p}^4}{\varepsilon_0\,m_p}}=
\sqrt[{\Large 3}\leftroot{4}\uproot{2}]{\frac{(1.602{\times}10^{\text{-}19})^4}{8.85{\times}10^{\text{-}12}{\times}1.674{\times}10^{\text{-}27}}}\\[1ex]
&=3.543{\times}10^{\text{-}13}\ [\mathrm{m}]
\end{align}
$$
また、俺さま単位での速度 1.0 の実値 $v_u$ は次のようになります。
$$
\begin{align}
&1\ [\mathsf{mo}\ \mathsf{so}^{\text{-}1}]=1\ [\ r_u\ [\mathrm{m}]\ (t_u\ [\mathrm{s}])^{\text{-}1}]=r_u/t_u\ [\mathrm{m}/\mathrm{s}]\\[1ex]
&\hspace{1em}=r_u/e_p\ [\mathrm{m}/\mathrm{s}]=3.543{\times}10^{\text{-}13}/1.602{\times}10^{\text{-}19}\\[1ex]
&\hspace{1em}=2.212{\times}10^{6}\ [\mathrm{m}/\mathrm{s}]=v_u\ [\mathrm{m}/\mathrm{s}]
\end{align}
$$
したがって、このシミュレーションでは、照射速度をアルファ線(光速の1/20程度で約1.5万 [km/s])に合わせるように、 $v_0{=}7$ に設定して、実速度を $7v_u{=}15.48{\times}10^{6}\ [\mathrm{m}/\mathrm{s}]$ としています。最終的に、図27のグラフは、上記 $r_u$ によって目盛りの数値を変換すれば、$\varepsilon_0$, $e_p$, $m_p$, $v_0$, $r_0$ の生の値を用いてシミュレーションした結果と完全に一致します。
金の原子核の半径は約 $7.2{\times}10^{\text{-}15}$ [m]、原子間距離は $2.884{\times}10^{\text{-}10}$ [m] とのことなので、グラフ上の目盛りでは、それぞれを $r_u$ で割った値の 0.02 と 814 に相当することになります。$b$ の値の 0.0641 と比べると、原子間距離の 814 はかなり大きく、殆どが素通りしてしまう計算になります。したがって、照射側に戻ってくる確率は相当に低くなることは分かりますが、これだけでは、広く伝えられている「8000個に1つ」の根拠は分かり兼ねます(素人考えでは、確率はもっと低くなりそうなのですが・・・)。
8.おわりに
以上、複素数がシミュレーションにも活用できることを詳細に説明して、複素数の利用が大変有効であることを力説しました。納得いただけましたでしょうか?
さて、最初に宣言した「複素数方式の適用の限界」ですが、記事を書き終わるまでには何か気づくことがあるはずだという期待があったため、最後には適用限界外の具体例を明示しながら説明できるだろうと思っていました。しかし、なかなか良い例を思いつきません。残念ながら、曖昧な表現での記述しかできませんが・・・。
複素数方式の適用の限界
-
複素数の状態変数どうしの乗除算が現れたときには注意が必要。
基本的に、複素数の状態変数どうしの結合は、実数係数による一次結合だけが許される。
ただし、角度を変換するための $i$ や $e^{i\theta}$ との乗除算や、生の複素数そのままでなく絶対値化した状態変数との乗除算の使用なら問題はなさそう。 -
スカラー量 と 実軸方向のベクトル との区別がつき難く、注意が必要なこともありそう。
9.プログラム
このプログラムでは、別記事(【MATLABユーザー定義関数】自由度が高い「subplotの変種」- Qiita)で紹介したユーザー定義関数 make_axes_freely と make_axes_tidily を利用している箇所があります。シミュレーションの本質とは関係ないので説明は割愛しますが、スクリプト中に axes(hax(n)) が現れた場合には、figure(n) と同等だと解釈すれば大丈夫です。
9.1 回転座標(実在の力=0)( 図5 )
% coriolis14am.m
% Simulinkモデルの coriolis14.slx 用プログラム
% コリオリの力と遠心力のシミュレーション(実在の力=0)
clear
close all
% グラフ用紙の準備(末尾に記述しているローカル関数の呼び出し)
[hax,hsp] = make_axes();
% simulinkのモデルのファイル名を指定。
Model='coriolis14'; % ファイル名: coriolis14.slx
% simulinkのモデルファイルを開く。
open_system(Model);
% 定数の設定(殆どは、ほぼモデル内の既定値どおりだが、ダメ押しの再設定)
set_param([Model '/init_Position'],'Value','0.12');
% 質点の初期位置 |r_0|=0.12[m]
set_param([Model '/Velocity_s'],'Value','0.5');
% 質点の静止座標上の速度 |v_s|=1[m/s]
set_param([Model '/Ang_velocity'],'Value','8.17');
% 座標の角速度 ω=3.49[rad/s]
set_param([Model '/Frd'],'Value','0');
% 回転座標表現の力 Fr'=0[N]
set_param([Model '/Fs'],'Value','0');
% 静止座標表現の力 Fs=0[N]
set_param([Model '/Mass'],'Value','0.01');
% 質点の質量 m=0.01[kg]
set_param(Model,'StopTime','1.2');
% シミュレーション時間[s]
set_param([Model '/To Workspace'],'SampleTime','0.01');
% サンプル時間[s]
% 軌跡の線が折れ線にならない程度に。
% 静止座標上での質点の移動方向φ[rad](実軸が0、反時計回りが正)
phi_data={'0' 'pi/3' '2*pi/3' 'pi' '-2*pi/3' '-pi/3'};
color={'b',[0.7 0.7 1],[1 0.7 0.7],'m'}; % グラフ線色の事前宣言
for p=1:length(phi_data) % 各種移動方向について繰り返す
set_param([Model '/Direction'],'Value',phi_data{p});
% 質点の進行方向 φ[rad]
axes(hax(p)); % 第p座標面の呼び出し
plot([-0.8 0.8 NaN 0 0],[0 0 NaN -0.8 0.8],'Color',[0.5 0.5 0.5]);
% 原点で交叉する座標軸
hold on
axis equal;
xlim([-0.8 0.8]);
ylim([-0.8 0.8]);
grid on
for n=1:4 % n=1: 座標変換による軌跡
% 2: 運動方程式による軌跡(コリオリの力のみ考慮)
% 3: 〃 (遠心力のみ考慮)
% 4: 〃 (両方とも考慮)
switch n
case 1
% 何もせず(座標変換のケースではどうでも良い)
case 2
set_param([Model '/Cor'],'Gain','-2i');
set_param([Model '/Cf'],'Gain','0');
case 3
set_param([Model '/Cor'],'Gain','0');
set_param([Model '/Cf'],'Gain','1');
case 4
set_param([Model '/Cor'],'Gain','-2i');
set_param([Model '/Cf'],'Gain','1');
otherwise
error('ERROR');
end
outcome=sim(Model); % Simulink のシミュレーションを開始し、
% その結果を To Workspace 経由で
% 変数 outcome に受け取る。
D1=outcome.simout.signal1.Data;
% 運動方程式による位置r
% (複素数の列ベクトル)
D2=outcome.simout.signal2.Data;
% 座標変換による位置r
% (複素数の列ベクトル)
TT=outcome.simout.signal1.Time;
% 時刻の列ベクトル(ここでは不使用)
% 時間信号 t は To Workspace に
% 意識的には引き込んでいないが、
% 自動的に入ってくる。
if n==1 % 座標変換
h1=plot(real(D2),imag(D2),'Color',color{1},'LineWidth',4);
elseif n==2 % コリオリのみ考慮の運動方程式
h2=plot(real(D1),imag(D1),'Color',color{n},'LineWidth',1);
elseif n==3 % 遠心力のみ考慮の運動方程式
h3=plot(real(D1),imag(D1),'Color',color{n},'LineWidth',1);
else % 両方とも考慮の運動方程式
% 背後に隠されてしまった座標変換による曲線を最前面に配置替え。
h = get(gca,'Children');
ind=(h==h1); % グラフの構成要素から h1 を探し、
newh = [h(ind); h(~ind)]; % それを表示の最上面に移動して
set(gca,'children',newh); % 描画順序を再構成。
% このさらに最上面に、最新の線を追加描画
h4=plot(real(D1),imag(D1),'Color',color{n},'LineWidth',1);
end
end
text(-0.75,0.70,[ ...
'直進方向 = ' get_param([Model '/Direction'],'Value') ...
' [rad]'],'FontSize',10);
box on
end
axes(hsp(5)); % figure領域全面に広がる座標面の呼び出し
text(20,166,[ ...
'直進速度 = ' get_param([Model '/Velocity_s'],'Value') ...
' [m/s]'],'FontSize',10);
text(20,161,[ ...
'座標角速度 = ' get_param([Model '/Ang_velocity'],'Value') ...
' [rad/s]'],'FontSize',10);
text(20,156,[ ...
'初期位置 = ' get_param([Model '/init_Position'],'Value') ...
' [m]'],'FontSize',10);
text(20,151,[ ...
'時間 = 0 ~ ' get_param(Model,'StopTime') ...
' [s]'],'FontSize',10);
legend([h1,h4,h2,h3],{'座標変換による軌跡','運動方程式による軌跡', ...
'同・コリオリの力のみ考慮','同・遠心力のみ考慮'}, ...
'Location',[0.752 0.74 0.215 0.1], ...
'FontSize',10,'EdgeColor','b','LineWidth',0.5);
% simulinkの各種パラメータの設定変更値は保存せずに閉じる。
close_system(Model,0);
% ===========================================================
% グラフ用紙の準備。
% シミュレーションの本質とは関係ないので、最後尾にまとめた。
function [hax,hsp] = make_axes();
% グラフ配置の調整用
m2=30; % 下余白[mm]
m3=22; % 左余白[mm]
W=65; % 座標面の幅[mm]
H=65; % 座標面の高さ[mm]
gw=2; % 座標面間の横方向の隙間[mm]
gh=25; % 座標面間の縦方向の隙間[mm]
Wp=W+gw; % 座標面配置の横方向のピッチ[mm]
Hp=H+gh; % 座標面配置の縦方向のピッチ[mm]
% 座標面の配置を指示するための行列
Maxes=[
m3+3*Wp m2+Hp/2 W H
m3+2*Wp m2+1*Hp W H
m3+1*Wp m2+1*Hp W H
m3+0*Wp m2+Hp/2 W H
m3+1*Wp m2+0*Hp W H
m3+2*Wp m2+0*Hp W H
];
% 座標面生成用の関数(別ファイル)を呼び出す。
[hax,hsp,h_number] = make_axes_freely('A4', 'land', Maxes);
delete(h_number);
for n=1:6
axes(hax(n));
xticks([-8:2:8]*0.1);
yticks([-8:2:8]*0.1);
if n==4
label={'-8','-6','-4','-2','0','2','4','6','8'};
xticklabels(label);
yticklabels(label);
xlabel('位置 [10^{-1}m]');
ylabel('位置 [10^{-1}m]');
else % 座標の諸量の重複表示はくどいので避ける
xticklabels({' '});
yticklabels({' '});
end
hold on
end
axes(hsp(5)); % figureの全面へアクセス
text(109,108,'回転座標から見た直進質点の軌跡','FontSize',14);
hold on
text(18,180,'図5','FontSize',20,'FontWeigh','bold')
end
9.2 回転座標(実在の力も考慮)( 図7,8 )
% coriolis18am.m
% Simulinkモデルの coriolis18.slx 用プログラム
% コリオリの力と遠心力のシミュレーション(実在の力を考慮)
clear
close all
% simulinkのモデルのファイル名を指定。
Model='coriolis18'; % ファイル名: coriolis18.slx
% simulinkのモデルファイルを開く。
open_system(Model); % coriolis18.slx
% 定数の設定(殆どは、ほぼ既定値どおりだが、ダメ押しの再設定)
set_param([Model '/init_Position'],'Value','10');
% 質点の初期位置(@回転座標)[m]
set_param([Model '/init_Velocity'],'Value','0');
% 質点の初期速度(@回転座標)[m/s]
set_param([Model '/Ang_velocity'],'Value','1');
% 回転座標の角速度 ω[rad/s]
set_param([Model '/Frd'],'Value','0');
% 回転座標表現の力 Fr'[N]
set_param([Model '/Fs'],'Value','0');
% 静止座標表現の力 Fs[N]
set_param([Model '/Mass'],'Value','1');
% 質点の質量[kg]
set_param(Model,'StopTime','200');
% シミュレーション時間[s]
set_param([Model '/To Workspace'],'SampleTime','0.1');
% サンプル時間[s]
% 軌跡の線が折れ線にならない程度に。
% グラフ用紙の準備(1枚目)(末尾に記述しているローカル関数の呼び出し)
[hax,hsp] = make_axes();
axes(hsp(1));
text(-140,15,'図7','FontSize',20)
text(-100,15,'回転座標上の実在の力 Fr'' による軌跡の変化','FontSize',16)
% 計算すべき Fr' 値のリスト
Fr_case={'20 + 0i', '10 + 0i', '0 + 0i', '-7 + 0i', '-13 + 0i', ...
'-20 + 0i', '-30 + 0i', '-40 + 0i'};
for p=1:length(Fr_case) % 各種Fr'値について繰り返す
set_param([Model '/Frd'],'Value',Fr_case{p});
axes(hax(p)); % 第p座標面の呼び出し
outcome=sim(Model); % Simulink のシミュレーションを開始し、
% その結果を To Workspace 経由で
% 変数 outcome に受け取る。
D1=outcome.simout.signal1.Data;
% 回転座標上の位置r'
% (複素数の列ベクトル)
D2=outcome.simout.signal2.Data;
% 固定座標上の位置r
% (複素数の列ベクトル)
TT=outcome.simout.signal1.Time;
% 時刻の列ベクトル(ここでは不使用)
% 時間信号 t は To Workspace に
% 意識的には引き込んでいないが、
% 自動的に入ってくる。
set(gca,'ColorOrderIndex',1); % グラフの線色順序をリセット
h1=plot(real(D1),imag(D1),'LineWidth',1);
h2=plot(real(D2),imag(D2),'LineWidth',1);
title(['Fr'' = ' Fr_case{p}],'FontSize',10)
box on
if p==1
legend([h1 h2],{'回転座標から観測した軌跡', ...
'静止座標から観測した軌跡'},'FontSize',10, ...
'Position',[0.79 0.83 0.1 0.05])
end
end
set_param([Model '/Frd'],'Value','0');
% 回転座標表現の力 Fr'[N]
% オリジナルの設定に戻す。
% グラフ用紙の準備(2枚目)(末尾に記述している関数の呼び出し)
[hax,hsp] = make_axes();
axes(hsp(1));
text(-140,15,'図8','FontSize',20)
text(-100,15,'静止座標上の実在の力 Fs による軌跡の変化','FontSize',16)
% 計算すべき Fs 値のリスト
Fs_case={'0 + 5i', '0 + 2i', '0 + 1i', '0 - 0i', '0 - 0.2i', ...
'0 - 0.5i', '0 - 1i', '0 - 2i'};
for p=1:length(Fs_case) % 各種Fs値について繰り返す
set_param([Model '/Fs'],'Value',Fs_case{p});
axes(hax(p)); % 第p座標面の呼び出し
outcome=sim(Model);
D1=outcome.simout.signal1.Data;
D2=outcome.simout.signal2.Data;
TT=outcome.simout.signal1.Time;
set(gca,'ColorOrderIndex',1); % グラフの線色順序をリセット
h1=plot(real(D1),imag(D1),'LineWidth',1);
h2=plot(real(D2),imag(D2),'LineWidth',1);
title(['Fs = ' Fs_case{p}],'FontSize',10)
box on
if p==1
legend([h1 h2],{'回転座標から観測した軌跡', ...
'静止座標から観測した軌跡'},'FontSize',10, ...
'Position',[0.79 0.83 0.1 0.05])
end
end
% simulinkの各種パラメータの設定変更値は保存せずに閉じる。
close_system(Model,0);
% ===========================================================
% グラフ用紙の準備。
% シミュレーションの本質とは関係ないので、最後尾にまとめた。
function [hax,hsp] = make_axes();
% 座標面生成用の関数(別ファイル)を呼び出す。
[hax,hsp,h_number] = make_axes_tidily('A4', 'land', ...
[2 4],[62 62],[43 32 28 12]);
delete(h_number);
labelx={'-300','-200','-100','0','100','200',' '};
labely={'-300','-200','-100','0','100','200','300'};
for n=1:8
axes(hax(n));
xticks([-3:3]*100);
yticks([-3:3]*100);
xticklabels({' '}); % 取敢えず、目盛数字は全部削除
yticklabels({' '}); % 〃
if n==1 || n==5
yticklabels(labely);
ylabel('位置 [m]');
end
if n>=5
xticklabels(labelx);
xlabel('位置 [m]');
end
hold on
plot([-300 300 NaN 0 0],[0 0 NaN -300 300],'Color',[0.5 0.5 0.5]);
% 原点で交叉する座標軸
axis equal;
xlim([-300 300]);
ylim([-300 300]);
grid on
end
end
9.3 回転座標(MATLAB ode45)( 図10 )
% coriolis14bm.m
% Simulinkモデルの
% coriolis14.slx, coriolis18.slx の動作を MATLAB の ode45 で再現。
% コリオリの力と遠心力のシミュレーション
clear
close all
% グラフ用紙の準備(1枚目)(末尾に記述している関数の呼び出し)
[hax,hsp] = make_axes();
axes(hsp(1));
text(-125,15,'図10','FontSize',20)
text(-70,15,'ルンゲクッタ法による軌跡','FontSize',16)
for model=1:3
% model=1; 実在の力なし(静止座標上の等速直進運動)
% model=2; 実在の力あり(回転座標上の力)
% model=3; 実在の力あり(静止座標上の力)
if model==1
Rs0=0.12; % init_Position
Vs=0.5; % Velocity_s
Ph=pi; % Direction
Ww=8.17; % Ang_velocity
Vr0=Vs*exp(i*Ph)-i*Ww*Rs0; % init_Velocity
Fr=0; % Frd
Fs=0; % Fs
Mm=0.01; % Mass
Ts=1.2; % StopTime
dT=0.01; % SampleTime
else
Rs0=10; % init_Position
Vr0=0; % init_Velocity
Ww=1; % Ang_velocity
Mm=1; % Mass
Ts=200; % StopTime
dT=0.1; % SampleTime
if model==2
Fr=10+0i; % 実在の力(回転座標)
Fs=0; % 実在の力(静止座標)
else % model==3
Fr=0; % 実在の力(回転座標)
Fs=0-1i; % 実在の力(静止座標)
end
end
% ==========================
% 複素数のままでルンゲクッタ
% ==========================
[t,y]=ode45(@(t,y) rot_coord01(t,y,Ww,Fr,Fs,Mm), ...
[0:dT:Ts],[real(Rs0);imag(Rs0);real(Vr0);imag(Vr0)]);
axes(hax(model)) % Figure 代替の座標呼び出し
h1=plot(y(:,1),y(:,2),'b','LineWidth',4);
hold on
% ==============================
% 実数だけに変換してルンゲクッタ
% ==============================
Frx=real(Fr); Fry=imag(Fr); Fsx=real(Fs); Fsy=imag(Fs);
[t,y]=ode45(@(t,y) rot_coord02(t,y,Ww,Frx,Fry,Fsx,Fsy,Mm), ...
[0:dT:Ts],[real(Rs0);imag(Rs0);real(Vr0);imag(Vr0)]);
h2=plot(y(:,1),y(:,2),'m','LineWidth',1);
axis equal
if model==1
axis([-8 8 -8 8]/10);
else
axis([-300 300 -300 300]);
end
grid on
end
legend([h1,h2],{'複素数のままでルンゲクッタ', ...
'実数だけに変換してルンゲクッタ'}, ...
'Location',[0.625 0.724 0.215 0.05], ...
'FontSize',10,'EdgeColor','b','LineWidth',0.5);
% ===========================================================
% 状態方程式の function
% (複素数のままでルンゲクッタ)
function dydt=rot_coord01(t,y,Ww,Fr,Fs,Mm)
% y(1),y(2): 位置の実部(x成分)と虚部(y成分)
% y(3),y(4): 速度の実部(x成分)と虚部(y成分)
% Ww:角速度、Fr:回転座標の実在の力(複素数)
% Mm:質量、 Fs:静止座標の実在の力(複素数)
r = y(1) + i*y(2); % 実部・虚部に分離して受け取った
v = y(3) + i*y(4); % データを合成して複素数を再現。
% 複素数による状態方程式の記述
drdt = v;
dvdt = Fs*exp(-i*Ww*t)/Mm + Fr/Mm - i*2*Ww*v + Ww^2*r;
dydt = zeros(4,1); % dydt が列ベクトルであることを宣言
dydt(1) = real(drdt); % 複素数として得られた drdt, dvdt を
dydt(2) = imag(drdt); % 実部・虚部に分離してから返す。
dydt(3) = real(dvdt);
dydt(4) = imag(dvdt);
end
% ===========================================================
% 状態方程式の function
% (実数だけに変換してルンゲクッタ)
function dydt=rot_coord02(t,y,Ww,Frx,Fry,Fsx,Fsy,Mm)
% y(1),y(2): 位置のx成分とy成分
% y(3),y(4): 速度のx成分とy成分
% Ww: 角速度、Frx,Fry: 回転座標の実在の力のx成分とy成分
% Mm: 質量、 Fsx,Fsy: 静止座標の実在の力のx成分とy成分
dydt = zeros(4,1); % dydt が列ベクトルであることを宣言
dydt(1) = y(3);
dydt(2) = y(4);
dydt(3) = Ww^2*y(1) + 2*Ww*y(4) + Frx/Mm ...
+ cos(Ww*t)*Fsx/Mm + sin(Ww*t)*Fsy/Mm;
dydt(4) = Ww^2*y(2) - 2*Ww*y(3) + Fry/Mm ...
- sin(Ww*t)*Fsx/Mm + cos(Ww*t)*Fsy/Mm;
end
% ===========================================================
% グラフ用紙の準備。
% シミュレーションの本質とは関係ないので、最後尾にまとめた。
function [hax,hsp] = make_axes();
% 座標面生成用の関数(別ファイル)を呼び出す。
[hax,hsp,h_number] = make_axes_tidily('A4', 'land', ...
[1 3],[62 62],[43 82 28 42]);
delete(h_number);
for n=1:3 % モデルに応じて座標を準備
axes(hax(n));
hold on
plot([-300 300 NaN 0 0],[0 0 NaN -300 300],'Color',[0.5 0.5 0.5]);
% 原点で交叉する座標軸
axis equal;
xlabel('位置 [m]');
ylabel('位置 [m]');
if n==1
xlim([-0.8 0.8]);
ylim([-0.8 0.8]);
title('直進方向 = pi [rad]')
xticks(yticks);
else
xlim([-300 300]);
ylim([-300 300]);
if n==2
title('Fr'' = 10 + 0i')
else
title('Fs = 0 - 1i')
end
end
grid on
box on
end
end
9.4 フーコーの振り子、気象現象( 図12,13,14,16,17,18 )
% coriolis19am.m
% フーコーの振り子、気象現象の風
clear
close all
% simulinkのモデルのファイル名を指定。
Model='coriolis19'; % ファイル名: coriolis19.slx
% ■■■■■■
% フーコーの振り子(外縁部から解放したとき)
% ■■■■■■
% simulinkのモデルファイルを開く。
open_system(Model);
set_param([Model '/SW_pos'],'Value','1');
% 切替スイッチ「フーコーの振り子」
set_param([Model '/K_Spring'],'Value','pi^2');
% ばね係数[N/m]
set_param([Model '/Mass'],'Value','3600^2');
% 質点の質量[kg]
set_param([Model '/Damping'],'Gain','0');
% 制動係数
set_param([Model '/Cor'],'Gain','-2i');
% コリオリの係数
set_param([Model '/Cf'],'Gain','1');
% 遠心力
set_param([Model '/init_Position'],'Value','5');
% 質点の初期位置(@回転座標)[m]
set_param([Model '/init_Velocity'],'Value','0');
% 質点の初期速度(@回転座標)[m/s]
set_param([Model '/Ang_Vel_e'],'Value','pi/43200');
% 地球の自転の角速度 [rad/s]
% set_param([Model '/Latitude'],'Value','35');
% 北緯の度 [deg]
set_param([Model '/Rs'],'Value','0');
% STOPブロック用 fcn を OFF
set_param([Model '/XY Graph'], 'xmin','-5');
set_param([Model '/XY Graph'], 'xmax','5');
set_param([Model '/XY Graph'], 'ymin','-5');
set_param([Model '/XY Graph'], 'ymax','5');
set_param([Model '/XY Graph1'],'xmin','-5');
set_param([Model '/XY Graph1'],'xmax','5');
set_param([Model '/XY Graph1'],'ymin','-5');
set_param([Model '/XY Graph1'],'ymax','5');
% XYスコープの座標範囲を指定
set_param(Model,'StopTime','43200');
% シミュレーション時間[s]、半日
set_param([Model '/To Workspace'],'SampleTime','10');
% サンプル時間[s]
set_param([Model '/To Workspace'],'Decimation','10');
% データの間引き
% グラフの座標面の準備(別ファイルのユーザー定義関数の呼び出し)
[hax,hsp,h_number] = make_axes_tidily('A4', 'land', ...
[2 4],[62 62],[52 32 25 12]);
delete(h_number);
axes(hsp(1))
text(-141,17,'図12','FontSize',20)
text(-108,17.5,'フーコーの振り子の軌跡(外縁部から解放、12時間)', ...
'FontSize',16)
% 計算すべき緯度の値[度]のリスト
Lat_case={'90', '45', '30', '10'};
for p=1:length(Lat_case) % 各種の緯度について繰り返す
set_param([Model '/Latitude'],'Value',Lat_case{p});
outcome=sim(Model); % Simulink のシミュレーションを開始し、
% その結果を To Workspace 経由で
% 変数 outcome に受け取る。
D1=outcome.simout.signal1.Data;
% 回転座標上の位置r'
% (複素数の列ベクトル)
D2=outcome.simout.signal2.Data;
% 固定座標上の位置r
% (複素数の列ベクトル)
TT=outcome.simout.signal1.Time;
% 時刻の列ベクトル(ここでは不使用)
% 時間信号 t は To Workspace に
% 意識的には引き込んでいないが、
% 自動的に入ってくる。
axes(hax(p)); % 第p座標面の呼び出し
hold on
set(gca,'ColorOrderIndex',1); % 第1線色で描画
h1=plot(real(D1),imag(D1),'LineWidth',1);
plot(real(D1(1)),imag(D1(1)),'ob','LineWidth',2);
plot(real(D1(end)),imag(D1(end)),'or','LineWidth',2);
xticks([-5:5]);
yticks([-5:5]);
grid on
xlim([-5 5]);
ylim([-5 5]);
box on
title([' 北緯' Lat_case{p} '°'],'FontSize',12)
xticklabels(' ');
if p==1
yticklabels({' ' '-4' ' ' '-2' ' ' '0' ' ' '2' ' ' '4' ' '});
axp=get(gca);
axp.YAxis.FontSize = 10;
ylabel('位置 [m]');
else
yticklabels(' ');
end
axes(hax(p+4)); % 第p+4座標面の呼び出し
hold on
set(gca,'ColorOrderIndex',2); % 第2線色で描画
h2=plot(real(D2),imag(D2),'LineWidth',1);
h3=plot(real(D2(1)),imag(D2(1)),'ob','LineWidth',2);
h4=plot(real(D2(end)),imag(D2(end)),'or','LineWidth',2);
xticks([-5:5]);
yticks([-5:5]);
grid on
xlim([-5 5]);
ylim([-5 5]);
box on
axp=get(gca);
xticklabels({' ' '-4' ' ' '-2' ' ' '0' ' ' '2' ' ' '4' ' '});
axp.XAxis.FontSize = 10;
if p==1
yticklabels({' ' '-4' ' ' '-2' ' ' '0' ' ' '2' ' ' '4' ' '});
axp.YAxis.FontSize = 10;
xlabel('位置 [m]');
ylabel('位置 [m]');
else
yticklabels(' ');
xlabel('位置 [m]');
end
end
lgd=legend([h1 h2 h3 h4],{'回転座標上','静止座標上','始点','終点'}, ...
'Location',[0.74 0.8 0.2 0.05],'FontSize',11);
lgd.NumColumns=2; % 凡例を2列にする。
% ■■■■■■
% フーコーの振り子(中心部から射出したとき)
% ■■■■■■
% 一部の条件を変える(初期位置に相当する初期速度の算出)
iP=get_param([Model '/init_Position'],'Value');
KS=get_param([Model '/K_Spring'],'Value');
Ma=get_param([Model '/Mass'],'Value');
iV=num2str( -sqrt(str2num(KS)/str2num(Ma))*str2num(iP) );
% iPは複素数も可
set_param([Model '/init_Position'],'Value','0');
% 質点の初期位置(@回転座標)[m]
set_param([Model '/init_Velocity'],'Value',iV);
% 質点の初期速度(@回転座標)[m/s]
% グラフの座標面の準備
[hax,hsp,h_number] = make_axes_tidily('A4', 'land', ...
[2 4],[62 62],[52 32 25 12]);
delete(h_number);
axes(hsp(1))
text(-141,17,'図13','FontSize',20)
text(-108,17.5,'フーコーの振り子の軌跡(中心部から射出、12時間)', ...
'FontSize',16)
% 計算すべき緯度の値[度]のリスト
Lat_case={'90', '45', '30', '10'};
for p=1:length(Lat_case) % 各種の緯度について繰り返す
set_param([Model '/Latitude'],'Value',Lat_case{p});
outcome=sim(Model); % Simulink のシミュレーションを開始し、
% その結果を To Workspace 経由で
% 変数 outcome に受け取る。
D1=outcome.simout.signal1.Data;
% 回転座標上の位置r'
% (複素数の列ベクトル)
D2=outcome.simout.signal2.Data;
% 固定座標上の位置r
% (複素数の列ベクトル)
axes(hax(p)); % 第p座標面の呼び出し
hold on
set(gca,'ColorOrderIndex',1); % 第1線色で描画
h1=plot(real(D1),imag(D1),'LineWidth',1);
plot(real(D1(1)),imag(D1(1)),'ob','LineWidth',2);
plot(real(D1(end)),imag(D1(end)),'or','LineWidth',2);
xticks([-5:5]);
yticks([-5:5]);
grid on
xlim([-5 5]);
ylim([-5 5]);
box on
title([' 北緯' Lat_case{p} '°'],'FontSize',12)
xticklabels(' ');
if p==1
yticklabels({' ' '-4' ' ' '-2' ' ' '0' ' ' '2' ' ' '4' ' '});
axp=get(gca);
axp.YAxis.FontSize = 10;
ylabel('位置 [m]');
else
yticklabels(' ');
end
axes(hax(p+4)); % 第p+4座標面の呼び出し
hold on
set(gca,'ColorOrderIndex',2); % 第2線色で描画
h2=plot(real(D2),imag(D2),'LineWidth',1);
h3=plot(real(D2(1)),imag(D2(1)),'ob','LineWidth',2);
h4=plot(real(D2(end)),imag(D2(end)),'or','LineWidth',2);
xticks([-5:5]);
yticks([-5:5]);
grid on
xlim([-5 5]);
ylim([-5 5]);
box on
axp=get(gca);
xticklabels({' ' '-4' ' ' '-2' ' ' '0' ' ' '2' ' ' '4' ' '});
axp.XAxis.FontSize = 10;
if p==1
yticklabels({' ' '-4' ' ' '-2' ' ' '0' ' ' '2' ' ' '4' ' '});
axp.YAxis.FontSize = 10;
xlabel('位置 [m]');
ylabel('位置 [m]');
else
yticklabels(' ');
xlabel('位置 [m]');
end
end
lgd=legend([h1 h2 h3 h4],{'回転座標上','静止座標上','始点','終点'}, ...
'Location',[0.74 0.8 0.2 0.05],'FontSize',11);
lgd.NumColumns=2;
% ■■■■■■
% フーコーの振り子(遠心力無視による誤差)
% ■■■■■■
% グラフの座標面の準備
left=25; % 左余白
botm=32; % 下余白
gw1=2; % 横間隙・狭
gw2=8; % 横間隙・広
gh=10; % 縦間隙
aw=62; % 座標幅
ah=62; % 座標高さ
% 座標面の配置を指定する行列
Maxes=[
left botm+ah+gh aw ah % 1 1 2 5 6
left+1*aw+1*gw1 botm+ah+gh aw ah % 2 3 4 7 8
left botm aw ah % 5
left+1*aw+1*gw1 botm aw ah % 6
left+2*aw+1*gw1+gw2 botm+ah+gh aw ah % 3
left+3*aw+2*gw1+gw2 botm+ah+gh aw ah % 4
left+2*aw+1*gw1+gw2 botm aw ah % 7
left+3*aw+2*gw1+gw2 botm aw ah % 8
];
[hax,hsp,h_number] = make_axes_freely('A4', 'land', Maxes);
delete(h_number);
axes(hsp(1))
text(-141,17,'図14','FontSize',20)
text(-108,17.5,['フーコーの振り子の軌跡 (北極にて24時間、' ...
'遠心力無視による誤差)'],'FontSize',16)
text(-84,6,'遠心力も考慮','FontSize',13)
text(50,6,'遠心力は無視','FontSize',13)
set_param([Model '/Latitude'],'Value','90'); % 北緯90度
set_param(Model,'StopTime','43200*2');
% シミュレーション時間[s]、丸1日
for ncf=1:2 % 遠心力(考慮/無視)
if ncf==1
set_param([Model '/Cf'],'Gain','1');
else
set_param([Model '/Cf'],'Gain','0');
end
for nic=1:2 % 初期条件(外縁/中心)
if nic==1
set_param([Model '/init_Position'],'Value',iP);
% 質点の初期位置(@回転座標)[m]
set_param([Model '/init_Velocity'],'Value','0');
% 質点の初期速度(@回転座標)[m/s]
else
set_param([Model '/init_Position'],'Value','0');
% 質点の初期位置(@回転座標)[m]
set_param([Model '/init_Velocity'],'Value',iV);
% 質点の初期速度(@回転座標)[m/s]
end
Nax=(ncf-1)*4+(nic-1)*2+1; % 使用する座標面の番号
outcome=sim(Model); % Simulink のシミュレーションを開始し、
% その結果を To Workspace 経由で
% 変数 outcome に受け取る。
D1=outcome.simout.signal1.Data;
% 回転座標上の位置r'
% (複素数の列ベクトル)
axes(hax(Nax));
hold on
set(gca,'ColorOrderIndex',1); % 第1線色で描画
plot(real(D1),imag(D1),'LineWidth',1);
plot(real(D1(1)),imag(D1(1)),'ob','LineWidth',2);
plot(real(D1(end)),imag(D1(end)),'or','LineWidth',2);
xticklabels({' ' '-4' ' ' '-2' ' ' '0' ' ' '2' ' ' '4' ' '});
yticklabels({' ' '-4' ' ' '-2' ' ' '0' ' ' '2' ' ' '4' ' '});
axp=get(gca);
axp.XAxis.FontSize = 10;
axp.YAxis.FontSize = 10;
if (Nax==3 || Nax==7)
xlabel('位置 [m]');
end
if (Nax==1 || Nax==3)
ylabel('位置 [m]');
end
xticks([-5:5]);
yticks([-5:5]);
grid on
xlim([-5 5]);
ylim([-5 5]);
box on
% ===============
axes(hax(Nax+1));
hold on
set(gca,'ColorOrderIndex',1); % 第1線色で描画
plot(real(D1),imag(D1),'LineWidth',1);
plot(real(D1(1)),imag(D1(1)),'ob','LineWidth',2);
plot(real(D1(end)),imag(D1(end)),'or','LineWidth',2);
xticklabels(' ');
yticklabels(' ');
box on
if (Nax==1 || Nax==5)
xlim([4.1 5.1]);
ylim([-0.5 0.5]);
text(4.2,0.4,'左図の拡大(×10)','FontSize',12)
else
xlim([-0.01 0.01]);
ylim([-0.01 0.01]);
plot([-0.008 0.008],[0.008 0.008],'w','LineWidth',20)
text(-0.008,0.008,'左図の拡大(×500)','FontSize',12)
end
end
end
% simulinkの各種パラメータの設定変更値は保存せずに閉じる。
close_system(Model,0);
% ■■■■■■
% 傾度風
% ■■■■■■
% 軌跡グラフの背景にする地図を取得
[cdata,Lat,Lon]=get_mercator_map();
Wp=630;
[Xp,Yp]=meshgrid([1:Wp],[1:Wp]);
% 地図の中心:北緯 38 度・東経 137 度
[Lon2,Lat2,Hp]=AED_inv(137*pi/180,38*pi/180, ...
2000,2000,1000,1000,Wp,Xp,Yp);
[Xp,Yp]=mercator_conv(Lon(1),Lat(1),Lon(2),Lat(2), ...
size(cdata,2),size(cdata,1),Lon2,Lat2);
CC=zeros(size(Xp,1),size(Xp,2),3,'uint8');
for gyou=1:size(Xp,1)
for retsu=1:size(Xp,2)
CC(gyou,retsu,:)=cdata(Yp(gyou,retsu),Xp(gyou,retsu),:);
end
end
% 経緯線のデータ
lon3=137+[-17:17];
lat3=38+[-18:18];
[LON3,LAT3]=meshgrid(lon3,lat3);
LON3=[LON3;LON3(1,:)*NaN];
LAT3=[LAT3;LAT3(1,:)*NaN];
LON3=[LON3 LON3(:,1)*NaN]*pi/180;
LAT3=[LAT3 LAT3(:,1)*NaN]*pi/180;
% simulinkのモデルファイルを開く。
open_system(Model);
set_param([Model '/SW_pos'],'Value','2');
% 切替スイッチ「傾度風」
set_param([Model '/Grad_Force'],'Value','0.001');
% 気圧傾度力[N/m^3]
set_param([Model '/Mass'],'Value','1.29');
% 質点の質量[kg]
set_param([Model '/Damping'],'Gain','0');
% 制動係数
set_param([Model '/Cor'],'Gain','-2i');
% コリオリの係数
set_param([Model '/Cf'],'Gain','0');
% 遠心力
set_param([Model '/init_Position'],'Value','6e5');
% 質点の初期位置(@回転座標)[m]
%set_param([Model '/init_Velocity'],'Value','7.8i');
% 質点の初期速度(@回転座標)[m/s]
set_param([Model '/Ang_Vel_e'],'Value','pi/43200');
% 地球の自転の角速度 [rad/s]
set_param([Model '/Latitude'],'Value','38');
% 北緯の度 [deg]
set_param([Model '/Rs'],'Value','0');
% STOPブロック用 fcn を OFF
set_param([Model '/XY Graph'], 'xmin','-8e5');
set_param([Model '/XY Graph'], 'xmax','8e5');
set_param([Model '/XY Graph'], 'ymin','-8e5');
set_param([Model '/XY Graph'], 'ymax','8e5');
set_param([Model '/XY Graph1'],'xmin','-8e5');
set_param([Model '/XY Graph1'],'xmax','8e5');
set_param([Model '/XY Graph1'],'ymin','-8e5');
set_param([Model '/XY Graph1'],'ymax','8e5');
% XYスコープの座標範囲を指定
%set_param(Model,'StopTime','400000');
% シミュレーション時間[s]
set_param([Model '/To Workspace'],'SampleTime','50');
% サンプル時間[s]
set_param([Model '/To Workspace'],'Decimation','10');
% データの間引き
% グラフの座標面の準備
[hax,hsp,h_number] = make_axes_tidily('A4', 'land', ...
[1 2],[100 100],[43 50 28 50]);
delete(h_number);
my_colors={'#0072BD','#080','#D95319'}; % 地味な紺、緑、赤
% 計算すべき気圧傾度力[N/m^3]、質点の初期速度[m/s]などのリスト
gF_case={'0.001', '-0.001'}; % 気圧傾度力
sT_case={'470000', '330000'}; % StopTime
iV_case={'3.8i', '15.2i', '7.6i'
'-5.5i', '-22i', '-10.9i'};
% 1行目:低気圧用、2行目:高気圧用
for p=1:length(gF_case)
set_param([Model '/Grad_Force'],'Value',gF_case{p});
% 気圧傾度力[N/m^3]
set_param(Model,'StopTime',sT_case{p});
% シミュレーション時間[s]
axes(hax(p)); % 第p座標面の呼び出し
CCf=flipud(CC);
image([-1000 1000],[-1000 1000],0.6*CCf+102); % 地図の貼り付け
axis xy
hold on
axis equal
xlim([-1000 1000]);
ylim([-1000 1000]);
% 経緯度線の描き込み
% ローカル関数の呼び出し(経緯度→基準点からの実距離)
[Lx,Ly]=AED_conv(137*pi/180,38*pi/180,LON3,LAT3);
plot(Lx,Ly,'w',Lx',Ly','w','LineWidth',1);
plot([0 0 NaN -1000 1000],[-1000 1000 NaN 0 0], ...
'Color','#888','LineWidth',2); % 直交座標軸
th=linspace(0,2*pi,101);
for rr=[400 800 1200]; % 等圧線
hh(1)=plot(rr*cos(th),rr*sin(th),'k','LineWidth',1);
end
if p==1
text(0,0,'低','FontSize',20,'HorizontalAlignment', 'center');
title('低気圧周りの傾度風(赤色)','FontSize',12);
else
text(0,0,'高','FontSize',20,'HorizontalAlignment', 'center');
title('高気圧周りの傾度風(赤色)','FontSize',12);
end
for q=1:size(iV_case,2)
set_param([Model '/init_Velocity'],'Value',iV_case{p,q});
% 質点の初期速度(@回転座標)[m/s]
outcome=sim(Model); % Simulink のシミュレーションを開始し、
% その結果を To Workspace 経由で
% 変数 outcome に受け取る。
D1=outcome.simout.signal1.Data;
% 回転座標上の位置r'
% (複素数の列ベクトル)
D1=D1/1000; % m → km
% 風の経路を描画
hh(q+1)=plot(real(D1),imag(D1),'LineWidth',2,'Color',my_colors{q});
if q==3
arx=real([D1(end-10) D1(end)]);
ary=imag([D1(end-10) D1(end)]);
[har]=plot_arrow(arx,ary,40,100);
har.Color=my_colors{q};
har.LineWidth=2;
end
box on
end
plot(600,0,'o','LineWidth',2,'Color','#D95319')
xlabel('距離 [km]');
ylabel('距離 [km]');
legend([hh(1) hh(2) hh(4) hh(3)], ...
{'等圧線',[iV_case{p,1} '[m/s]'], ...
[iV_case{p,3} '[m/s]'], ...
[iV_case{p,2} '[m/s]']},'Location','NorthWest');
end
axes(hsp(1))
text( -123,14,'図16','FontSize',20);
text(-48,14,'傾度風の軌跡 と 異風速の風の軌跡','FontSize',16);
% simulinkの各種パラメータの設定変更値は保存せずに閉じる。
close_system(Model,0);
% ■■■■■■
% 台風の渦
% ■■■■■■
% 軌跡グラフの背景にする地図を取得
Wp=630;
[Xp,Yp]=meshgrid([1:Wp],[1:Wp]);
% 地図の中心:北緯 30 度・東経 132 度
[Lon2,Lat2,Hp]=AED_inv(132*pi/180,30*pi/180, ...
2000,2000,1000,1000,Wp,Xp,Yp);
[Xp,Yp]=mercator_conv(Lon(1),Lat(1),Lon(2),Lat(2), ...
size(cdata,2),size(cdata,1),Lon2,Lat2);
CC=zeros(size(Xp,1),size(Xp,2),3,'uint8');
for gyou=1:size(Xp,1)
for retsu=1:size(Xp,2)
CC(gyou,retsu,:)=cdata(Yp(gyou,retsu),Xp(gyou,retsu),:);
end
end
% グラフの座標面の準備
[hax,hsp,h_number] = make_axes_tidily('A4', 'land', ...
[1 2],[100 100],[43 50 28 50]);
delete(h_number);
% 台風の気圧配置
rr=linspace(0,2000,201);
rm=80;
Pi=1013;
P0=940;
Pt=Pi-(Pi-P0)./sqrt(1+(rr/rm).^2);
axes(hax(1));
plot(rr,Pt,'b','LineWidth',1);
hold on
axis([0 2000 0 1200]);
grid on
xlabel('台風の中心からの距離 [km]');
ylabel('気圧 [hPa]');
title('台風の気圧分布','FontSize',12);
% 台風の等圧線
axes(hax(2));
% 背景地図
CCf=flipud(CC);
image([-1000 1000],[-1000 1000],0.6*CCf+102); % 地図の貼り付け
axis xy
hold on
axis equal
xlim([-1000 1000]);
ylim([-1000 1000]);
% 経緯度線の描き込み
% ローカル関数の呼び出し(経緯度→基準点からの実距離)
[Lx,Ly]=AED_conv(132*pi/180,30*pi/180,LON3,LAT3);
plot(Lx,Ly,'w',Lx',Ly','w','LineWidth',1);
% 等圧線
Rep=interp1(Pt,rr,[P0:4:Pi]);
th=linspace(0,2*pi,101);
for n=1:length(Rep)
hep=plot(Rep(n)*cos(th),Rep(n)*sin(th),'k');
if (n==1 | n==6 | n==11 | n==16)
hep.LineWidth=1;
end
end
xlabel('距離 [km]');
ylabel('距離 [km]');
title('台風の等圧線 ( 4 [hPa] 間隔 )','FontSize',12);
axes(hsp(1))
text( -123,14,'図17','FontSize',20);
text(-23,14,'台風周辺の気圧','FontSize',16);
% simulinkのモデルファイルを開く。
open_system(Model);
set_param([Model '/SW_pos'],'Value','3');
% 切替スイッチ「台風の渦」
set_param([Model '/dP'],'Value','7300');
% 藤田の式の係数
set_param([Model '/Rm'],'Value','0.8e5');
% 藤田の式の係数
set_param([Model '/Mass'],'Value','1.29');
% 質点の質量[kg]
set_param([Model '/Damping'],'Gain','10e-6');
% 制動係数
set_param([Model '/Cor'],'Gain','-2i');
% コリオリの係数
set_param([Model '/Cf'],'Gain','0');
% 遠心力
set_param([Model '/init_Position'],'Value','1e6');
% 質点の初期位置(@回転座標)[m]
set_param([Model '/init_Velocity'],'Value','0');
% 質点の初期速度(@回転座標)[m/s]
set_param([Model '/Ang_Vel_e'],'Value','pi/43200');
% 地球の自転の角速度 [rad/s]
set_param([Model '/Latitude'],'Value','30');
% 北緯の度 [deg]
set_param([Model '/Rs'],'Value','4000');
% STOPブロック用 fcn を OFF
set_param([Model '/XY Graph'], 'xmin','-4e6');
set_param([Model '/XY Graph'], 'xmax','4e6');
set_param([Model '/XY Graph'], 'ymin','-4e6');
set_param([Model '/XY Graph'], 'ymax','4e6');
set_param([Model '/XY Graph1'],'xmin','-4e6');
set_param([Model '/XY Graph1'],'xmax','4e6');
set_param([Model '/XY Graph1'],'ymin','-4e6');
set_param([Model '/XY Graph1'],'ymax','4e6');
set_param([Model '/XY Graph2'],'xmin','0');
set_param([Model '/XY Graph2'],'xmax','4e6');
set_param([Model '/XY Graph2'],'ymin','0');
set_param([Model '/XY Graph2'],'ymax','50');
% XYスコープの座標範囲を指定
set_param(Model,'StopTime','3e7');
% シミュレーション時間[s]、半日
set_param([Model '/To Workspace'],'SampleTime','1000');
% サンプル時間[s]
set_param([Model '/To Workspace'],'Decimation','1');
% データの間引き
% グラフの座標面の準備
[hax,hsp,h_number] = make_axes_tidily('A4', 'land', ...
[1 2],[100 100],[43 50 28 50]);
delete(h_number);
outcome=sim(Model); % Simulink のシミュレーションを開始し、
% その結果を To Workspace 経由で
% 変数 outcome に受け取る。
D1=outcome.simout.signal1.Data;
% 回転座標上の位置r'
% (複素数の列ベクトル)
D3=outcome.simout.signal3.Data;
% 固定座標上の速度v'
% (複素数の列ベクトル)
D1=D1/1000; % m → km
axes(hax(1)); % 第1座標面の呼び出し
CCf=flipud(CC);
image([-1000 1000],[-1000 1000],0.6*CCf+102); % 地図の貼り付け
axis xy
hold on
axis equal
xlim([-1000 1000]);
ylim([-1000 1000]);
% 経緯度線の描き込み
% ローカル関数の呼び出し(経緯度→基準点からの実距離)
[Lx,Ly]=AED_conv(132*pi/180,30*pi/180,LON3,LAT3);
plot(Lx,Ly,'w',Lx',Ly','w','LineWidth',1);
plot([0 0 NaN -1000 1000],[-1000 1000 NaN 0 0], ...
'Color','#888','LineWidth',2); % 直交座標軸
plot(real(D1),imag(D1),'LineWidth',1);
axis equal;
axis([-1000 1000 -1000 1000]);
xlabel('距離 [km]');
ylabel('距離 [km]');
title('台風の渦','FontSize',12);
axes(hax(2)); % 第2座標面の呼び出し
plot(abs(D1),abs(D3),'LineWidth',1);
axis([0 1000 0 45]);
grid on
xlabel('中心からの距離 [km]');
ylabel('風速 [m/s]');
title('台風の風速','FontSize',12);
axes(hsp(1))
text( -123,14,'図18','FontSize',20);
text(-23,14,'台風の渦 と 風速','FontSize',16);
% simulinkの各種パラメータの設定変更値は保存せずに閉じる。
close_system(Model,0);
% ■■■■■■
% ローカル関数一式
% ■■■■■■
% ===========================================================
% グラフ用紙の準備。
% シミュレーションの本質とは関係ないので、最後尾にまとめた。
function [hax,hsp] = make_axes();
% 座標面生成用の関数(別ファイル)を呼び出す。
[hax,hsp,h_number] = make_axes_tidily('A4', 'land', ...
[2 4],[62 62],[43 32 28 12]);
delete(h_number);
labelx={'-300','-200','-100','0','100','200',' '};
labely={'-300','-200','-100','0','100','200','300'};
for n=1:8
axes(hax(n));
xticklabels({' '}); % 取敢えず、目盛数字は全部削除
yticklabels({' '}); % 〃
if n==1 || n==5
yticklabels(labely);
ylabel('位置 [m]');
end
if n>=5
xticklabels(labelx);
xlabel('位置 [m]');
end
hold on
plot([-300 300 NaN 0 0],[0 0 NaN -300 300],'Color',[0.5 0.5 0.5]);
% 原点で交叉する座標軸
axis equal;
xlim([-5 5]);
ylim([-5 5]);
grid on
end
end
% ===========================================================
% メルカトル地図を原画像として取得
% 注:Windows のディスプレイの「拡大/縮小」が「150%」の場合。
% 「100%」にすると、このままでは取得領域が狭くなるので要注意。
function [cdata,Lat,Lon] = get_mercator_map()
hf=figure(10);
wp=1000;
hp=680;
hf.Position=[100 10 wp hp];
gx=geoaxes('Basemap','colorterrain');
gx.MapCenterMode = 'manual';
gx.MapCenter=[36 135];
gx.ZoomLevel=5.3;
gx.Position = [0 0 1 1];
gx.Grid='off';
Lat=(gx.LatitudeLimits)*pi/180;
Lon=(gx.LongitudeLimits)*pi/180;
set(gcf,'PaperUnits','inches','PaperPosition',[0 0 wp/10 hp/10])
cdata = print('-RGBImage','-r15');
close 10
end
% ========================================================
% 【正距方位図法の画素インデックス → 経緯度】変換
function [Lon,Lat,Hp]=AED_inv(lon0,lat0,W,H,w0,h0,Wp,Xp,Yp)
% 【入力】
% lon0,lat0 : 正距方位図の基準点の経度・緯度[radian]
% W.H : 〃 の幅と高さ[km]
% w0,h0 : 基準点を置く位置(地図左下隅からの距離)[km]
% Wp : 正距方位図の幅として割り当てるピクセル数[px]
% Xp,Yp : 画素位置の列と行のペア
% (左上画素が1列1行、右下画素がWp列Hp行)
% (Hpはこのfunctionの中で決まる。YpにHp超の画素を)
% (含むときは、Hp行の画素を指定されたものとみなす)
% 【出力】
% Lon,Lat : 指定画素の中心部分の経度・緯度のペア[radian]
% (Xp,Yp と同一サイズ)
% Hp : 正距方位図の高さとして割り当てるピクセル数[px]
% (現実には存在しない余分な行を切り捨てるのに利用)
dD=W/Wp; % 1px長に相当する距離[km/px]
Re=6371; % 地球の平均半径[km]
Hp=round(H/dD); % 地図の縦方向のピクセル数[px](整数)
% 正距方位図の基準点を置く位置
w0p=w0/dD; % 地図左端からのピクセル数[px](浮動小数)
h0p=h0/dD; % 地図下端 〃 [px](浮動小数)
n_over=find(Yp>Hp); % 指定された図の高さ(H)の範囲に収まらない画
Yp(n_over)=Hp; % 素は、その範囲の境界線の色と同一色とする。
% 基準点から指定ピクセルの中心位置までの、地球上における実距離
Xr=((Xp-0.5)-w0p)*dD; % 基準点から東方向への実距離[km]
Yr=((Hp-Yp+0.5)-h0p)*dD; % 基準点から北方向への実距離[km]
% 変換式
c=sqrt(Xr.^2+Yr.^2)/Re;
alpha=atan2(Xr,Yr);
Lat=asin(sin(lat0)*cos(c)+cos(lat0)*cos(alpha).*sin(c));
Lon=atan2(sin(c).*sin(alpha), ...
cos(lat0)*cos(c)-sin(lat0)*cos(alpha).*sin(c))+lon0;
end
% ========================================================
% 【経緯度 → メルカトル地図上の画素インデックス】変換
function [Xp,Yp]=mercator_conv(lon1,lat1,lon2,lat2,Wp,Hp,Lon,Lat)
% 【入力】
% 表示領域が下記で与えられたメルカトル地図の画像があるとする。
% (とりあえず、±180度の経度を跨ぐ領域は考えていない)
% lon1,lat1 : 地図の左下隅の経度・緯度[radian]
% lon2,lat2 : 地図の右上隅の経度・緯度[radian]
% Wp,Hp : 地図のサイズ(横 Wp ピクセル×縦 Hp ピクセル)
% この地図上から、下記の指定経緯度の点のピクセル位置を返す。
% Lon,Lat : 指定点の経度・緯度のペア[radian]
% (同一サイズの スカラーか ベクトルか 行列)
% 【出力】
% Xp,Yp : 画素位置の列と行のペア。Lon,Lat と同一サイズ。
% (左上画素が1列1行、右下画素がmm列nn行)
k=Wp/(lon2-lon1); % 地図の倍率 [pixel/経度radian]
% 東経0度・北緯0度を原点にした、地図上の各点の位置
% (単位:pixel、浮動小数)
xmin=k*lon1; % 地図の左下隅
ymin=k*log(tan(lat1/2+pi/4));
xmax=k*lon2; % 地図の右上隅
ymax=k*log(tan(lat2/2+pi/4));
if round(ymax-ymin)~=Hp
warning(['lat2 と Hp の関係にズレがあります。' ...
'結果は正確ではありません。' newline ...
' round(ymax-ymin)=' num2str(round(ymax-ymin)) ...
' Hp=' num2str(Hp)])
end
% 入力経緯度 Lon,Lat に対応する位置(単位:pixel、浮動小数)
% 地図の左下隅を原点とした右手系デカルト座標
X=k*Lon-xmin;
Y=k*log(tan(Lat/2+pi/4))-ymin;
% 境界上に存在する判定が微妙なデータが、
% 丸め誤差により異常値を出力しないよう、防止のため前処理。
vv=find(X<=0);
X(vv)=X(vv)+0.001;
vv=find(X>=Wp);
X(vv)=X(vv)-0.001;
vv=find(Y<=0);
Y(vv)=Y(vv)+0.001;
vv=find(Y>=Hp);
Y(vv)=Y(vv)-0.1; % ここだけやや厳しくしておく
% 上記 X,Y から、画像の左上隅の画素を
% (1,1)とした画素座標(整数)に変換する。
Xp=ceil(X); % イメージ行列中での各画素の列
Yp=Hp-ceil(Y)+1; % 〃 行
end
% ========================================================
% 【経緯度 → 正距方位図法の基準点からの実距離】変換
function [Lx,Ly]=AED_conv(lon0,lat0,Lon,Lat)
% 【入力】
% lon0,lat0 : 正距方位図の基準点の経度・緯度[radian]
% Lon,Lat : 地図内の各点の経度・緯度のペア[radian]
% 【出力】
% Lx,Ly : Lon,Latに対応する点の、基準点からの位置[km]
Re=6371; % 地球の平均半径[km]
c=acos(sin(lat0)*sin(Lat)+cos(lat0)*cos(Lat).*cos(Lon-lon0));
alpha=atan2(sin(Lon-lon0),cos(lat0)*tan(Lat)-sin(lat0)*cos(Lon-lon0));
Lx=Re*c.*sin(alpha);
Ly=Re*c.*cos(alpha);
end
% ========================================================
% 矢印の頭の描画(二次元グラフ専用)
function [h_arw]=plot_arrow(xv,yv,ang,leng)
% 【入力】
% xv,yv : 矢印の頭の中心線の向き。
% (xv(1),yv(1)) → (xv(2),yv(2))
% ang : 矢印の両翼間の角度[度]
% leng : 矢印の両翼の長さ
% 【出力】
% h_arw : 矢印のハンドル
ang=ang*pi/180;
th0=atan2(yv(2)-yv(1),xv(2)-xv(1))+pi;
x0=xv(2); y0=yv(2);
x1=leng*cos(th0-ang/2)+x0; y1=leng*sin(th0-ang/2)+y0;
x2=leng*cos(th0+ang/2)+x0; y2=leng*sin(th0+ang/2)+y0;
h_arw=plot([x1 x0 x2],[y1 y0 y2],'k');
end
9.5 惑星軌道、ラザフォード散乱( 図20,21,22,26,27 )
% planet_orbit15am.m
% Simulinkモデルの planet_orbit15~18.slx 用プログラム
%
% 初期位置 r_0 固定の惑星軌道
% 初期速度 v_0 固定の惑星軌道
% 初期速度 v_0 固定の位置・速度・角度の時間変化
% 初期速度 v_0 固定の惑星軌道(保存量の利用有無による計算精度の差)
% ラザフォード散乱の軌跡
clear
close all
% 使用する Simulink のブロック線図のファイルのリスト
model_name={'planet_orbit15','planet_orbit16', ...
'planet_orbit17','planet_orbit18'};
for fig_num=1:2 % figure(1)(2)用の図枠の準備
figure(fig_num)
set(gcf,'Position',[200 100 840 500]); % 標準は[360 198 560 420]
% 標準よりも大き目の図。
plot([-14 4 NaN 0 0],[0 0 NaN -5 5],'k','LineWidth',1);
% 座標軸(原点:太陽)
hold on
end
% simulinkのモデルファイルを開く。
Model=model_name{1}; % まずは、保存量を使用しないときのブロック線図
open_system(Model);
% ■■■■■■
% 初期位置固定で初期速度を変化したときの惑星軌道
% ■■■■■■
figure(1);
% 初期位置(実軸上の 1)
r_0=1;
% 初期速度v_0のデータ(向き:虚軸の正方向)
v_0={'0.3' '0.7' '0.9' '1.0' '1.22' '1.306' '1.342' '1.36' ...
'1.4142' '1.55' '2'};
% 計算結果の間引き量を設定変更
set_param([Model '/To Workspace'],'Decimation','1');
% Solverは「可変ステップ」の「自動」のままで変更なし。
% (ブロック線図内の Configuration Parameter での設定どおり)
for G=[1 -1] % 万有引力定数(引力と斥力)
if G==-1
set(gca,'ColorOrderIndex',1); % グラフの線色順序をリセット
end
set_param([Model '/Grav_const'],'Value',num2str(G));
% モデル内の万有引力定数Gを設定変更
for n=1:length(v_0) % 初期速度の各値について順次実行
if str2num(v_0{n})<0.9 % 小軌道は発散ぎみゆえ、手厚く配慮
set_param(Model,'StopTime','4');
% シミュレーション時間を設定変更
set_param([Model '/To Workspace'],'SampleTime','0.001');
% サンプリング時間を設定変更
else
set_param(Model,'StopTime','150');
set_param([Model '/To Workspace'],'SampleTime','0.1');
end
set_param([Model '/init_Position'],'Value',num2str(r_0));
% モデル内の初期位置r_0を設定変更
set_param([Model '/init_Velocity'],'Value',v_0{n});
% モデル内の初期速度v_0を設定変更
outcome=sim(Model); % シミュレーションを開始し、
% 結果を outcome に出力。
Sim_Out=outcome.simout;
tt=Sim_Out.signal1.Time; % 時刻(実数の列ベクトル)
RR=Sim_Out.signal1.Data; % 惑星の位置(複素数の列ベクトル)
% VV=Sim_Out.signal2.Data; % 〃 速度( 〃 )
x=real(RR);
y=imag(RR);
% v_0=1.36の軌跡だけ、等時間間隔で〇印を追加プロットする。
% 時間間隔はε=0軌道の1周期相当(2π)とする。
if G==1 && n==8
yd=[1;y(2:end)]; % 最初の 0 は無視
ind=min(find(yd.*circshift(yd,-1)<=0)); % y のゼロクロス点検出
tcyc=interp1(y(ind-2:ind+2),tt(ind-2:ind+2),0)*2; % 運行周期
ts=[0:2*pi:max(tt)]'; % 〇印のプロット間隔
xys=interp1(tt,[x y],ts); % リサンプリング
idx=find(ts>=tcyc); % 軌跡の1周期分相当の
xys(idx,:)=[]; % 時間のデータ以外は廃棄。
end
% 軌道がグラフ圏外を大きく外れて上方に消えてしまったとき、
% 軌跡の上半分しか描かれないので、下半分を追加。
if min(imag(RR))>=0 % 位置の虚数部が0以上のとき、
% 上半分しか計算されていない。
x=[flipud(x);x]; % 上半分と下半分の軌跡を繋げる
y=[-flipud(y);y];
end
if G==1 % 引力の軌跡を描画
h1(n)=plot(x,y,'LineWidth',2);
else % 斥力の軌跡を描画
h2(n)=plot(x,y,':','LineWidth',1);
end
if G==1 && n==8 % 等時間間隔点をプロット
idc=get(gca,'ColorOrderIndex'); % 次の線色番号
if idc==1
idc=7; % 線色を一つ前に戻す
else
idc=idc-1; % 線色を一つ前に戻す
end
set(gca,'ColorOrderIndex',idc);
% もう一度、同色でグラフの〇印を描画
plot(xys(:,1),xys(:,2),'o','MarkerFaceColor','w');
end
end % end of "for n=1:length(v_0)"
end % end of "for G=[1 -1]"
axis equal; % x,y軸のスケールを同一にする(真円は真円に)
xlim([-14 4]);
ylim([-5 5]);
xticks([-14:4]);
grid on
title(['惑星軌道(保存量 不使用)' ...
'( G=±1, M=1, r_0=1 )'],'FontSize',14);
text(-14.8,5.5,'図20','FontSize',20,'FontWeigh','bold')
xlabel('Re');
ylabel('Im');
v_0x=v_0;
v_0x(1)={['v_0=' v_0x{1}]};
legend(h1,v_0x, ...
'Position',[0.094 0.098 0.110 0.329]);
text(-13.3,4.3,'実線:引力');
text(-13.3,3.8,'破線:斥力(参考)');
text(-1.1,1.1,'ε=0');
text(-5.1,-4.4,'ε=1');
% ■■■■■■
% 初期速度固定で初期位置を変化したときの惑星軌道
% ■■■■■■
figure(2);
% 初期速度(向き:虚軸方向)
v_0=1;
% 初期位置r_0のデータ
r_0={'0.3' '0.5' '0.75' '1.0' '1.25' '1.5' '1.75' ...
'2.0' '2.5' '3.0' '3.5' '4.0'};
% 計算結果の間引き
set_param([Model '/To Workspace'],'Decimation','1');
rv_curve={}; % 位置,速度,時間の曲線データ収納用のセル
period=[]; % 惑星の運行周期
for G=[1 -1] % 万有引力(引力と斥力)
if G==-1
set(gca,'ColorOrderIndex',1); % グラフの線色順序をリセット
end
% モデル内の万有引力定数Gを設定変更
set_param([Model '/Grav_const'],'Value',num2str(G));
for n=1:length(r_0) % 初期位置の各値について順次実行
if str2num(r_0{n})<0.75 % 小軌道は発散ぎみゆえ、手厚く配慮
set_param(Model,'StopTime','3');
% シミュレーション時間を設定変更
set_param([Model '/To Workspace'],'SampleTime','0.001');
% サンプリング時間を設定変更
else
set_param(Model,'StopTime','150');
set_param([Model '/To Workspace'],'SampleTime','0.1');
end
% モデル内の初期速度を設定変更
set_param([Model '/init_Velocity'],'Value',num2str(v_0));
% モデル内の初期位置r_0を設定変更
set_param([Model '/init_Position'],'Value',r_0{n});
outcome=sim(Model); % シミュレーションを開始し、
% 結果を outcome に出力。
Sim_Out=outcome.simout;
tt=Sim_Out.signal1.Time; % 時刻(実数の列ベクトル)
RR=Sim_Out.signal1.Data; % 惑星の位置(複素数の列ベクトル)
VV=Sim_Out.signal2.Data; % 〃 速度( 〃 )
x=real(RR);
y=imag(RR);
if G==1
% 楕円軌道の一部のデータを抽出・加工
% (位置・速度・角度の時間変化データを取得)
if n>=1 && n<=7
yd=[1;y(2:end)]; % 最初の 0 は無視
ind=min(find(yd.*circshift(yd,-1)<=0)); % y のゼロクロス検出
tcyc=interp1(y(ind-2:ind+2),tt(ind-2:ind+2),0)*2; % 運行周期
period=[period tcyc]; % 運行周期データの保持
idx=find(tt>=tcyc); % 運行周期を超えるデータの指標
rr=abs(RR);
vv=abs(VV);
phi=angle(VV./RR);
vt=vv.*sin(phi);
the=angle(RR);
idn=find(the<0); % -π ~ π のデータを
the(idn)=the(idn)+2*pi; % 0 ~ 2π に変換。
curve_data=[the rr vv vt tt];
curve_data(idx,:)=[]; % 周期分以外のデータは破棄
rv_curve={rv_curve{:} curve_data};
% 位置,速度,時間の曲線データの保持
end
% r_0=1.75の軌跡だけ、等時間間隔で〇印を追加プロットする。
% 時間間隔はε=0 軌道の1周期相当(2π)とする。
if n==7
ts=[0:2*pi:max(tt)]'; % 〇印のプロット間隔
xys=interp1(tt,[x y],ts); % リサンプリング
idx=find(ts>=tcyc); % 軌跡の1周期分相当の
xys(idx,:)=[]; % 時間のデータ以外は廃棄。
end
end
% 軌道がグラフ圏外を大きく外れて上方に消えてしまったとき、
% 軌跡の上半分しか描かれないので、下半分を追加。
if min(imag(RR))>=0 % 位置の虚数部が0以上のとき、
% 上半分しか計算されていない。
x=[flipud(x);x]; % 上半分と下半分の軌跡を繋げる
y=[-flipud(y);y];
end
if G==1 % 引力の軌跡を描画
h1(n)=plot(x,y,'LineWidth',2);
else % 斥力の軌跡を描画
h2(n)=plot(x,y,':','LineWidth',1);
end
if G==1 && n==7
idc=get(gca,'ColorOrderIndex'); % 次の線色番号
if idc==1
idc=7; % 一つ前に戻す
else
idc=idc-1; % 一つ前に戻す
end
set(gca,'ColorOrderIndex',idc);
% もう一度、同色でグラフの〇印を描画
plot(xys(:,1),xys(:,2),'o','MarkerFaceColor','w');
end
end % end of "for n=1:length(r_0)"
end % end of "for G=[1 -1]"
axis equal; % x,y軸のスケールを同一にする(真円は真円に)
xlim([-14 4]);
ylim([-5 5]);
xticks([-14:4]);
grid on
title(['惑星軌道(保存量 不使用)' ...
'( G=±1, M=1, v_0=1 )'],'FontSize',14);
text(-14.8,5.5,'図21','FontSize',20,'FontWeigh','bold')
xlabel('Re');
ylabel('Im');
r_0x=r_0;
r_0x(1)={['r_0=' r_0x{1}]};
legend(h1,r_0x, ...
'Position',[0.354 0.259 0.10 0.329]);
text(-13.3,4.3,'実線:引力');
text(-13.3,3.8,'破線:斥力(参考)');
text(-0.7,1.20,'ε=0');
text(-1.35,-4.45,'ε=1');
% ここでのブロック線図への設定変更は反映させずにファイルを閉じる。
% (ファイル内の設定値は、開く直前のデータのまま保持される)
close_system(Model,0)
% ■■■■■■
% figure(3) 惑星の位置や速度の時間変化
% ■■■■■■
% 1枚の用紙に14個の座標面を準備する(ローカル関数呼び出し)
% (自動的に、未使用で最小の figure 番号の figure(3) に設定される)
[hax,hsp] = make_axes01();
for n=1:length(rv_curve)
A=rv_curve{n};
axes(hax(n))
line1=semilogy(A(:,1)/pi,A(:,2),'LineWidth',2);
hold on
set(gca,'ColorOrderIndex',3); % 第3線色で描画
line2=semilogy(A(:,1)/pi,A(:,3));
set(gca,'ColorOrderIndex',2); % 第2線色で描画
line3=semilogy(A(:,1)/pi,A(:,4),'LineWidth',2);
ylim([0.05 20])
grid on
box on
title(['初期位置 r_0=' r_0{n}],'FontSize',11)
axes(hax(n+7));
line4=plot(A(:,1)/pi,A(:,5),'LineWidth',2);
set(gca,'ColorOrderIndex',1); % 線色順をリセット
line5=plot(A(:,1)/pi,A(:,5)*10,':','LineWidth',1);
text(0.1,100,['周期: ' num2str(period(n))],'FontSize',9);
ylim([0 120])
grid on
end
legend([line1 line3 line2],{'位置 | r |','速度のθ成分', ...
'速度 | v |'},'Position',[0.5 0.52 0.12 0.06],'FontSize',9);
legend([line4 line5],{'時間','同拡大(10倍)'}, ...
'Position',[0.3 0.35 0.12 0.042],'FontSize',9);
axes(hsp(1)); % 上部スペースにアクセス
text(-65,16,'動径の角度 vs 位置,速度,時間( G=1, M=1, v_0=1 )', ...
'FontSize',16);
hold on
text(-141,17,'図22','FontSize',20,'FontWeigh','bold')
% ■■■■■■
% 4種類の Simulink モデルの性能比較
% ■■■■■■
% Simulinkモデルの planet_orbit15~18.slx の計算結果の差を確認
% シミュレーション条件を落としたうえ、一部分のグラフ拡大での比較。
% (v_0:1i 固定、r_0:各種、G:1)
v_0=1; % 初期速度 向き:虚軸方向
r_0={'0.3' '0.5'}; % 初期位置r_0のデータ
G=1; % 万有引力定数
title_str= {
'保存量は不使用', ...
'保存量 L のみ利用', ...
'保存量 ε のみ利用', ...
'保存量 ε,L とも利用'
};
s_time={'0.004' '0.006' '0.012'}; % サンプリング時間3種
% 1枚の用紙に12個の座標面を準備する(ローカル関数呼び出し)
% (自動的に、未使用で最小の figure 番号の figure(4) に設定される)
[hax,hsp] = make_axes02(title_str, s_time);
for mm=1:4 % Simulinkモデル4ケースについて
% simulinkのモデルファイルを開く。
open_system(model_name{mm});
% 計算結果の間引き量を設定変更
if mm==1
set_param([model_name{mm} '/To Workspace'],'Decimation','1');
else
set_param([model_name{mm} '/Observer/To Workspace'], ...
'Decimation','1');
end
set_param([model_name{mm} '/Grav_const'],'Value',num2str(G));
% 万有引力定数Gを設定変更
set_param([model_name{mm} '/init_Velocity'],'Value',num2str(v_0));
% 初期速度を設定変更
% ソルバーを設定変更(固定ステップの ode4 を指定)
% (この figure 以外では、可変ステップの自動を利用している)
set_param(model_name{mm},'Solver','ode4');
for ns=1:3 % サンプリング時間の各値について
axes(hax((ns-1)*4+mm)); % 該当の座標面をアクティブにする
for n=1:length(r_0) % 初期位置の各値について順次実行
set_param(model_name{mm},'StopTime','10');
% シミュレーション時間を設定変更
% サンプリング時間を設定変更
if mm==1
set_param([model_name{mm} '/To Workspace'], ...
'SampleTime',s_time{ns});
else
set_param([model_name{mm} '/Observer/To Workspace'], ...
'SampleTime',s_time{ns});
end
set_param([model_name{mm} '/init_Position'],'Value',r_0{n});
% モデル内の初期位置r_0を設定変更
outcome=sim(model_name{mm}); % シミュレーションを開始し、
% 結果を outcome に出力。
Sim_Out=outcome.simout;
RR=Sim_Out.signal1.Data; % 惑星の位置(複素数の列ベクトル)
x=real(RR);
y=imag(RR);
plot(x,y,'b-');
end % for n=1:length(r_0) の end
end % for ns=1:3 の end
% ここでのブロック線図への設定変更は反映させずにファイルを閉じる。
% (ファイル内の設定値は、開く直前のデータのまま保持される)
close_system(model_name{mm},0)
end % for mm=1:4 の end
axes(hsp(1)); % 上部スペースにアクセス
text(-50,18,'4種類のブロック線図の性能比較','FontSize',16);
hold on
text(-140,17,'図26','FontSize',20,'FontWeigh','bold')
% ■■■■■■
% ラザフォード散乱
% ■■■■■■
figure(5)
set(gcf,'Position',[200 100 840 500]); % 標準は[360 198 560 420]
% 標準よりも大き目の図。
hold on
plot([-0.1 0.1 NaN 0 0],[0 0 NaN -0.1 0.1], ...
'Color',[1 1 1]*0.5,'LineWidth',1);
plot(0,0,'or','MarkerFaceColor','r','MarkerSize',9);
% 原点:金の原子核の位置
% simulinkのモデルファイルを開く。
Model='planet_orbit15'; % 惑星軌道用のモデルを流用
open_system(Model);
v_0=7i; % 初期速度(Simulinkのブロック線図内でiが掛かる
% ので、実質i*i=-7 で、実軸の負の向きの速度)
G=-3.143; % 万有引力に換算した係数(斥力とする)
M=1; % ここでは、GM=-3.143 とするためだけの変数
% 初期位置r_0のデータ
r_0={'10+0.01i' '10+0.02i' '10+0.03i' '10+0.04i' ...
'10+0.06i' '10+0.0641i' '10+0.08i' '10+0.10i' ...
'10+0.14i' '10+0.20i' '10+0.30i' };
set_param([Model '/init_Velocity'],'Value',num2str(v_0));
% モデル内の初期速度を設定変更
set_param(Model,'StopTime','10');
% シミュレーション時間を設定変更
set_param([Model '/To Workspace'],'SampleTime','0.005');
% サンプリング時間を設定変更
set_param([Model '/To Workspace'],'Decimation','1');
% 計算結果の間引き量を設定変更
set_param([Model '/Grav_const'],'Value',num2str(G));
% 万有引力換算の定数Gを設定変更
set_param([Model '/Mass_Sun'],'Value',num2str(M));
% 定数Mを設定変更
set(gca,'ColorOrderIndex',1); % グラフの線色順序をリセット
clear h1; % ハンドル h1 を再利用
for n=1:length(r_0) % 初期位置の各値について順次実行
% モデル内の初期位置r_0を設定変更
set_param([Model '/init_Position'],'Value',r_0{n});
outcome=sim(Model); % シミュレーションを開始し、
% 結果を outcome に出力。
Sim_Out=outcome.simout;
tt=Sim_Out.signal1.Time; % 時刻(実数の列ベクトル)
RR=Sim_Out.signal1.Data; % α粒子位置(複素数の列ベクトル)
VV=Sim_Out.signal2.Data; % 〃 速度( 〃 )
x=real(RR);
y=imag(RR);
x=[x;NaN;x];
y=[-y;NaN;y];
h1(n)=plot(x,y,'LineWidth',1); % 軌跡の描画
end
% ここでのブロック線図への設定変更は反映させずにファイルを閉じる。
% (ファイル内の設定値は、開く直前のデータのまま保持される)
close_system(Model,0)
axis equal; % x,y軸のスケールを同一にする
xlim([-0.4 1.6]);
ylim([-0.6 0.6]);
text(-0.19,0.03,'金の原子核');
text(1.2,0.23,'アルファ線');
grid on
title([' ラザフォード散乱 ( \epsilon_0=1, e_p=1, m_p=1 )' ...
'=( GM=-3.143 相当 ) v_0=-7'],'FontSize',14);
text(-0.53,0.66,'図27','FontSize',20,'FontWeigh','bold')
xlabel('Re');
ylabel('Im');
r_0=strrep(r_0,'+','±'); % 初期位置の文字列中の'+'を'±'に置換
r_0(1)={['r_0=' r_0{1}]};
legend(h1,r_0,'Position',[0.75 0.146 0.143 0.348]);
% ■■■■■■
% ローカル関数一式
% ■■■■■■
% ==================================================
% 1枚の用紙に14個の座標面を準備する
function [hax,hsp] = make_axes01();
% カスタム座標面 生成用 ユーザー関数(別ファイル)の呼び出し
% 座標面構成:35mm×55mm×2行×7列
[hax,hsp,h_number] = make_axes_tidily ...
('A4','land',[2 7],[35 55],[50 48 25 15]);
delete(h_number); % 座標面名の表示を削除
for n=1:14
axes(hax(n))
% hold on 前のダミープロット
if n<=7
semilogy(NaN,NaN);
xticks([0 0.5 1 1.5 2])
yticks([0.1 0.2 0.5 1 2 5 10 20])
else % n>=8
plot(NaN,NaN);
xticks([0 0.5 1 1.5 2])
yticks([0 20 40 60 80 100 120])
end
set(gca,'ColorOrderIndex',1); % 線色順をリセット
xticklabels({''});
yticklabels({''});
if n==1
yticklabels({'0.1','0.2','0.5','1','2','5','10','20'})
ylabel(['太陽からの位置' ...
newline '速度、同・θ方向成分'],'FontSize',9);
end
if n>=8
xticklabels({'0','0.5','1','1.5','2'})
xlabel(['動径の角度' ...
newline '[\timesπ radian]'],'FontSize',9);
end
if n==8
yticklabels({'0','20','40','60','80','100','120'})
ylabel('時間','FontSize',9);
end
hold on
end
end
% ==================================================
% 1枚の用紙に12個の座標面を準備する
function [hax,hsp] = make_axes02(title_str, s_time);
% カスタム座標面 生成用 ユーザー関数(別ファイル)の呼び出し
% 座標面構成:60mm×42mm×3行×4列
[hax,hsp,h_number] = make_axes_tidily ...
('A4','land',[3 4], [60 42],[48 32 37 15]);
delete(h_number); % 座標面名の表示を削除
for nr=1:3; % 座標面群の行
for nc=1:4; % 座標面群の列
nn=(nr-1)*4+nc; % 座標面番号
axes(hax(nn)); % nn番目の座標をアクティブにする
plot([-0.3 0.7 NaN 0 0],[0 0 NaN -0.35 0.35], ...
'k','LineWidth',1); % 原点:太陽
hold on
xticks([-3:7]*0.1);
yticks([-3:3]*0.1);
axis equal; % x,y軸は同一スケール(真円は真円に)
grid on
xlim([-0.3 0.7]);
ylim([-0.35 0.35]);
if nc==1; % 第1列にある座標面(縦軸目盛ラベルを表示)
yticklabels({'-0.3','-0.2','-0.1','0','0.1','0.2','0.3'});
ylabel('Im');
text(-0.57,0,['時間刻み ' s_time{nr}],'FontSize',10, ...
'HorizontalAlign','center','Rotation',90);
else % 座標の冗長な重複表示はしない
yticklabels({''});
end
if nr==1; % 第1行にある座標面(Simulinkモデル名を表示)
text(0.2,0.45,title_str{nc},'FontSize',10, ...
'HorizontalAlign','center');
end
if nr==3; % 第3行にある座標面(横軸目盛ラベル等を表示)
label={'','-0.2','','0','','0.2','','0.4','','0.6',''};
xticklabels(label);
xlabel('Re');
else % 座標の冗長な重複表示はしない
xticklabels({''});
end
end
end
end