はじめに
MATLAB には、一枚のFigure上に複数の座標面を作るコマンドとして subplot が用意されています。また、R2019b以降の新しいバージョンでは、tiledlayout という新コマンドも登場しているようです。tiledlayout は subplot よりもさらに利便性が向上しているようですが、私の使用しているバージョンは R2019a と古いため、直接利用して比較することはできません![]() 。しかし、ヘルプセンターのマニュアルから判断する限りでは、ここで紹介する関数もまだまだ存在価値はありそうです
。しかし、ヘルプセンターのマニュアルから判断する限りでは、ここで紹介する関数もまだまだ存在価値はありそうです![]() 。
。
subplot を使っていて感じる不便さは次のようなものです。
- 隣の座標面との間隔を適正化し、座標面をもっと広くとりたい。
- 座標面の配置をもっと自由に、しかも楽にできるようにしたい。
- アスペクト比を崩さず、規格用紙への印刷を前提にしたレイアウトをしたい。
ところが、レイアウトを自分流にカスタマイズしようとしても、figure の位置決めの単位は pixel なのに対して、その内部の座標面の位置決めの単位は normalized とバラバラです。しかも、normalized は縦と横ではスケールが異なるので、操作が煩雑でなかなかやる気が起きません。(既定として設定されている単位は変更することもできるようですが、予期せぬ問題が起こりそうで、軽々しく触るのは憚られます。)
そこで、これらの不便さを解消するために、下記の2種類のユーザー定義関数を作ってみました。これらに共通した最大の特徴は、座標面の位置や寸法を、規格サイズの用紙上の[mm]単位で指定できることです。これにより、まず、バラバラだった単位系の煩わしさから解放されます。
- make_axes_tidily.m(以下、tidily版と略)
均等に整列させた同一サイズの複数の座標面を作ったり、それらの一部をまとめたりすることができます。subplot と似ていますが自由度と使い易さが向上しています。 - make_axes_freely.m(以下、freely版と略)
位置と大きさを座標面ごとに自由に指定できます。レイアウトを用紙上で予めデザインしてから使うときには、こちらの方が便利です。
詳細な利用方法は、添付プログラムの冒頭にあるhelp用の記述部に書いてあります。興味を持たれた方はそちらをご覧ください。また、各プログラムの最後には、利用例を記述したテスト用のプログラムを、コメント化した状態で添付してあります。以下に例示している画像はこのプログラムで描かれたものです。
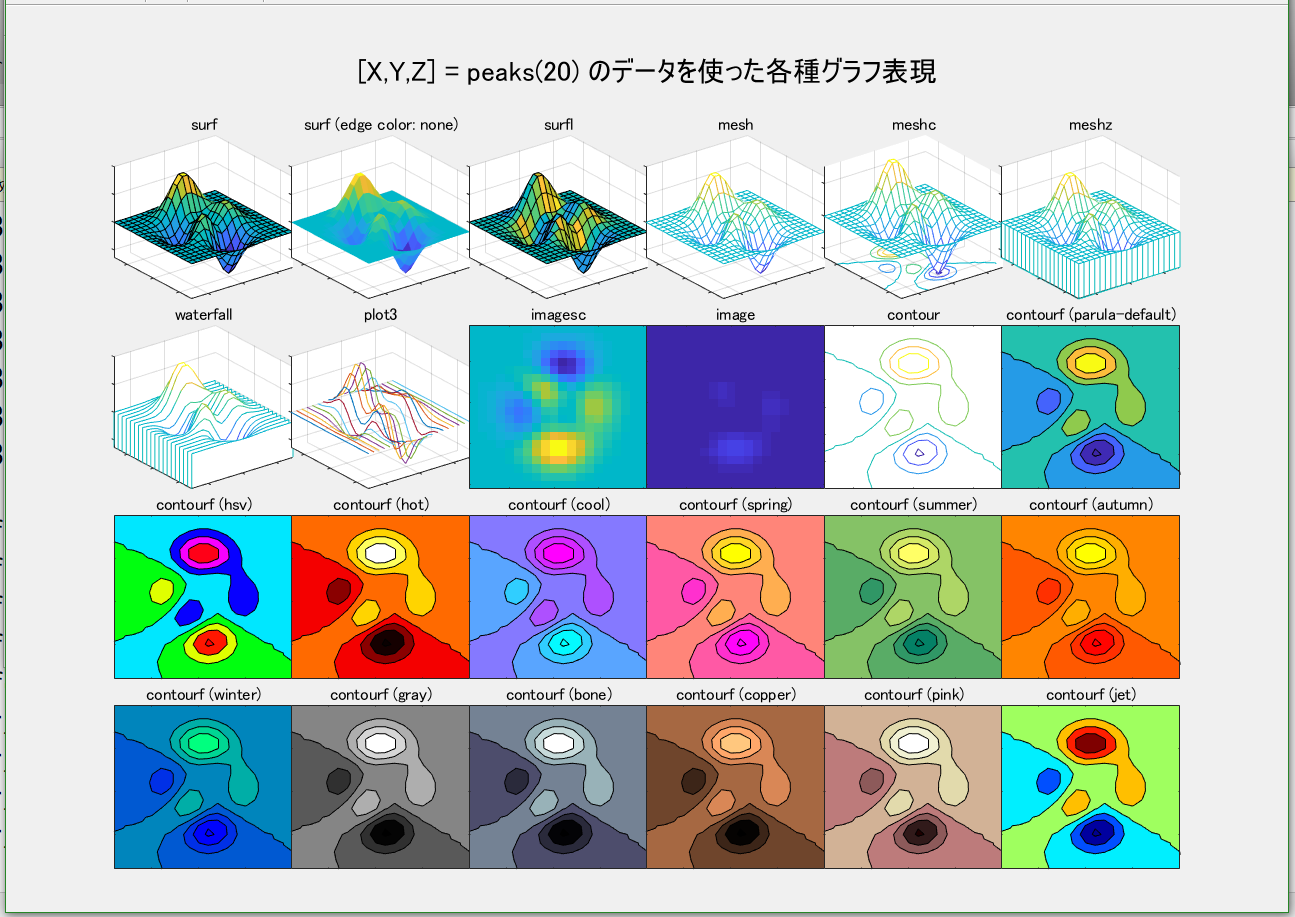
利用例1
tidily版による作図です。同一サイズの座標面が等間隔に配置されています。座標面の間の横方向の隙間は極限まで詰めてスペースの利用率を上げ、縦方向の隙間は、タイトルを書けるだけの必要最小限の間隔にしています。
カラーマップは、バー状の見本でみるよりも、具体的な図形で例示された方がイメージが伝わりやすいようです。なお、カラーマップの一つとして、ヘルプセンターのマニュアルに載っている turbo ですが、これを指定してもなぜか反応がありません。
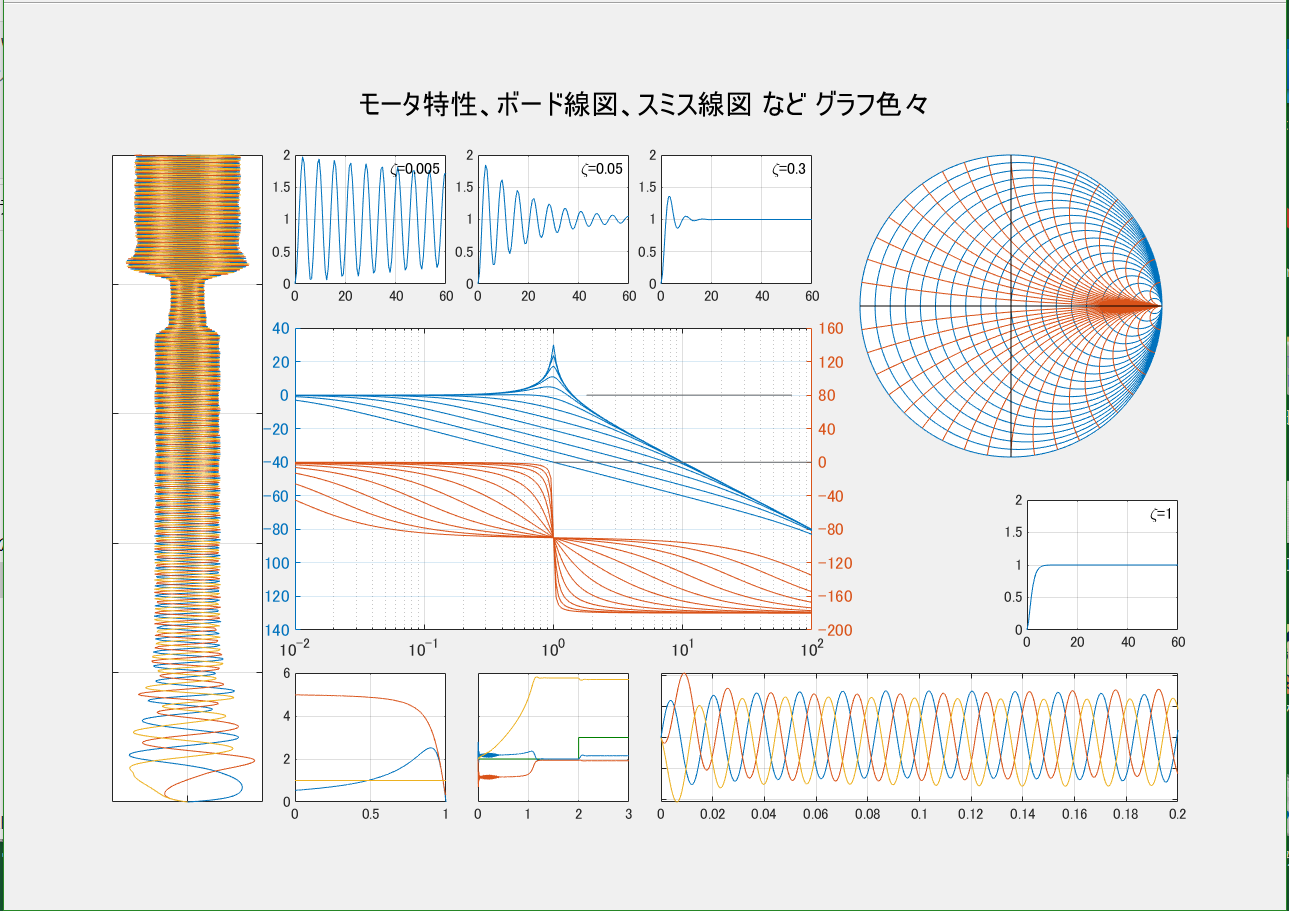
利用例2
これもtidily版による作図です。一部の座標面をグループ化して大きくしています。このユーザー定義関数の強みを生かせる良い利用例を思い付かなかったため、手抜き感があり、subplot による作図と変わらないようにも見えますが・・・。
ただし、モータの電流波形の作図には少々苦戦して、本題の関数の仕上げよりも時間がかかってしまいました。
利用例3
freely版による作図です。私のアバターの周辺に「いいね」マークが漂っている構図です![]() 。裸眼立体視できるように作図しています。4つのハートマークは、それぞれが独立した小さな座標面に描かれています。この座標面を正確かつ微妙に左右にずらすことで、奥行き方向の見える位置が変わります。なお、既述の2つの利用例では、規格用紙として A4 を指定していますが、本利用例では、印刷したときに立体視に適したサイズになるように A5 を指定しています。
。裸眼立体視できるように作図しています。4つのハートマークは、それぞれが独立した小さな座標面に描かれています。この座標面を正確かつ微妙に左右にずらすことで、奥行き方向の見える位置が変わります。なお、既述の2つの利用例では、規格用紙として A4 を指定していますが、本利用例では、印刷したときに立体視に適したサイズになるように A5 を指定しています。
姑息な手段で作図したハートマークが、予想外の出来で満足しています。
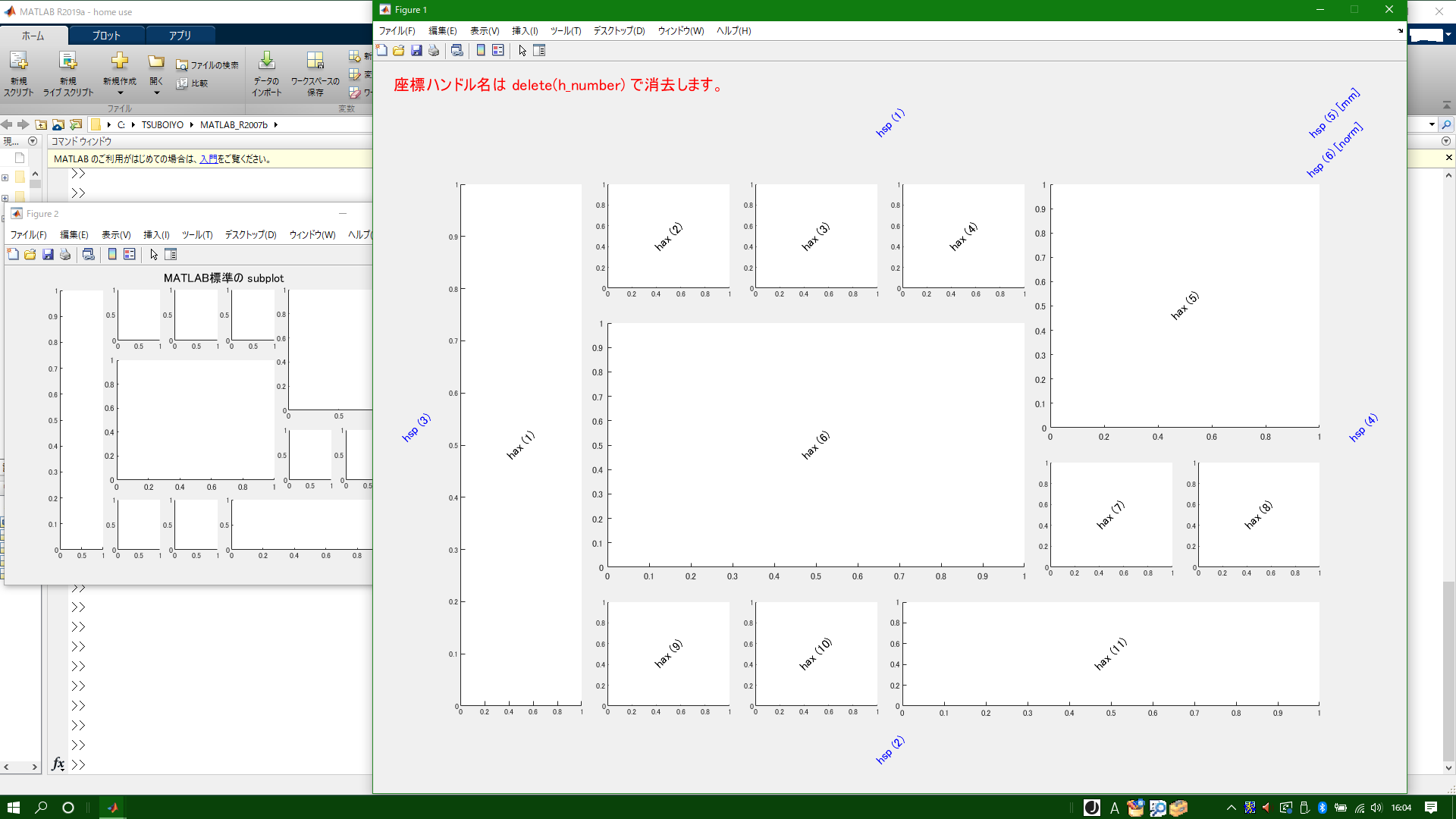
初期画面
MATLAB 標準の subplot 画面と並べて、まだ何も描かれていない初期画面を示しています。指定した用紙のアスペクト比を保ち、最大画面表示するような仕様になっています。また、アクセスする場合に必要になる各座標面のハンドル名も表示されています。座標面だけでなく、上下左右の余白や用紙全体へアクセスするためのハンドルもあります。
プログラム tidily版
function [hax,hsp,h_number] = make_axes_tidily ...
(pp_size, orient, struct, ax_size, margin, Mcomb)
%
% =======================
% make_axes_tidily ヘルプ
% =======================
%
% =====
% 概要:
% =====
%
% 第6引数 Mcomb を指定しないとき、
% 一枚の用紙に整然と並んだ同一寸法の複数の[座標面]を生成します。
% Mcomb を指定したとき
% これらの[座標面]をグループ化して大きな[座標面]に再構築します。
%
% このプログラムの末尾には、利用例のプログラムをコメント化して添付し
% ています。
%
% =====
% 特徴:
% =====
%
% 組み込みの subplot コマンドでは、既定で、[座標面]の周囲の余白が
% 広めに設定されているので、肝心の[座標面]が小さく見にくくなります。
% しかし、カスタマイズしようにも、figure や axes の Position を設定
% する単位として pixel や normalized が混在しており、さらに、
% normalized は縦と横でスケールが異なるので、調整には非常に苦労しま
% す。
%
% この make_axes_tidily 関数では、描画面として、パソコン画面ではな
% く規格サイズの用紙を想定し、[mm]単位でレイアウトを指定できるので、
% 異なる単位の混在による煩わしさがありません。また、画面上でも、
% figure 窓のリサイズを禁止し、アスペクト比を重視しながら最大画面表
% 示させるので、細部まで見やすく、印刷結果も画面上のレイアウトと殆ど
% 差がありません。
%
% グループ化が必要ない場合、関数の呼び出し時に入力する情報は、用紙
% サイズ(A4など)、縦置き横置きの別、[座標面]の縦×横の各配置数、[座
% 標面]のサイズ、用紙の上下左右の各余白の幅 だけです。必要最小限に絞
% っているので簡単に使えます。
%
% また、[座標面]のサイズ、上下左右の各余白の幅 は、一気に正確に入
% 力する必要はありません。試行錯誤で入力値を変更し、画面全体の配置を
% 目視で確認しながら、納得できるまで調整することができます。
%
% グループ化する場合でも、その指示情報をまとめた1つの行列を入力す
% るだけですから、なにも面倒なことはありません。
%
% =============
% 呼び出し形式:
% =============
%
% [hax,hsp,h_number] = make_axes_tidily ...
% (pp_size, orient, struct, ax_size, margin, Mcomb)
%
% =====
% 入力:
% =====
%
% pp_size: 印刷用紙のサイズ
% 'A3' = 297 * 420 [mm] ( 短辺 * 長辺 )
% 'B4' = 257 * 364 [mm]
% 'A4' = 210 * 297 [mm]
% 'B5' = 182 * 257 [mm]
% 'A5' = 149 * 210 [mm]
%
% orient: 印刷用紙の向き
% 'port' = 縦(portrait)
% 'land' = 横(landscape)
%
% struct: [座標面]群の配置
% [ 縦に並べる個数(行数) 横に並べる個数(列数) ]
%
% ax_size: 1つの[座標面]のサイズ。全[座標面]とも同一のサイズ。
% [ 幅[mm] 高さ[mm] ]
% 軸名、目盛数値、タイトル用のスペースは含めない。
%
% margin: 用紙の上下左右端に設ける余白
% [ 上余白[mm] 下余白[mm] 左余白[mm] 右余白[mm] ]
% [座標面]の外周部にある軸名・目盛数値・タイトルなどのスペ
% ースも余白領域に含まれる。
% 1行だけ、あるいは1列だけの[座標面]構成の場合の特例:
% 1行構成のとき、[座標面]の上下の位置決めに使用されるの
% は下余白だけ。上部の余りを、上余白値として自動修正。
% 1列構成のとき、[座標面]の左右の位置決めに使用されるの
% は左余白だけ。右側の余りを、右余白値として自動修正。
% 余白には軸が表示されないが、[座標面]並みの扱いが可能。
%
% Mcomb: 複数の[座標面]をグループ化して一つの大きな[座標面]を構成
% するときに、次の形式の行列で指定する。
% グループ化しないときには入力する必要はない。
%
% 行の基本は [ 左上のL 左上のC 右下のL 右下のC ]
%
% 例:
% [1 1 1 3] ■のグループ
% Mcomb = [2 1 3 1] ▲のグループ
% [2 3 3 5] ★のグループ
%
% C= 1 2 3 4 5 6
% L=1 ■■■□□・
% L=2 ▲□★★★・
% L=3 ▲□★★★・
% L=4 ・・・・・・
%
% =====
% 出力:
% =====
%
% hax: 各[座標面]へアクセスするためのハンドル
% hax(1), hax(2), ..., hax(j) [座標面]へのハンドル
% ( j=struct(1)*struct(2) )
% ( )内のハンドル番号は、
% グループ化しないとき:
% 最上段の左の[座標面]から右方向にカウントしていく。
% 右端に達したら、次の下の段の左からカウントを続ける。
% (横書き文書の読み書き順に準じる。)
% グループ化したとき:
% 上記に準じ、[座標面]の左上隅が現れる順にカウント。
%
% hsp: 上下左右の各余白と紙面全面へアクセスするためのハンドル。
% 全領域とも axis off に設定しているので軸は表示されない。
% 領域内の原点
% hsp(1): 上余白 下端中央
% hsp(2): 下余白 上端中央
% hsp(3): 左余白 右端中央
% hsp(4): 右余白 左端中央
% hsp(5): 紙面全面 左下隅
% 以上、領域内での位置指定単位は[mm]
% hsp(6): 紙面全面 左下隅
% これだけは、領域内での位置指定単位は[normalized]
% legend などは normalized での位置指定が必要なため
%
% h_number: 初期画面に[座標面]へのハンドル名が表示されるが、これを消
% 去するためのハンドル。消去するには delete(h_number) と指
% 示する。
%
% ==========
% 使用方法:
% ==========
%
% MATLAB のコマンドラインからでも、プログラムからでも、まずは第6引数
% のことは考えないで、
% [hax,hsp,h_number] = make_axes_tidily ...
% ('A4','land',[4 6],[35 30],[30 30 25 25]);
% などと、希望しているレイアウトに近そうな値を入力して呼び出します。
%
% すると、すぐに、指定どおりに[座標面]が表示されます。上下左右の余
% 白と[座標面]の寸法を指定するだけなので、[座標面]の間隔は自動的に決
% まります。詰まり過ぎていれば、[座標面]同士で重なってしまうし、余裕
% があり過ぎると間が抜けます。気に入った状態になるまで入力値を調整し
% ます。
%
% この後、グループ化が必要であれば、第6引数に Mcomb を指定して、レ
% イアウトの仕上がりを確認します。
%
% レイアウトが決まったら、描画したい[座標面]を axes(hax(1)) 等で呼
% び出してから、普通の plot, mesh, text コマンドなどで描画します。
%
% なお、初期画面には、各[座標面]へのハンドル名が表示されています。
% 不要になった段階で、delete(h_number) で消去してください。
%
% 用紙への印刷は、[ファイル]-[印刷プレビュー]画面で、[用紙形式]と
% [印刷の向き]を入力の第1,第2引数に一致するように選択し、[配置]を
% [手動設定のサイズと位置を使用]として、[左]と[上]を0、[幅]と[高さ]
% を[用紙]の値と合わせてから行ってください。
%
% なお、画面上ではタイトルや目盛数値が思い通りに表示されているのに、
% 印刷してみると隣の[座標面]と重なったりすることもあります。印刷結果
% を重視する場合には、文字仕様などの再調整が必要なこともあります。
%
% =====
% 注意:
% =====
%
% 1. 上下左右の余白の幅の値として、完全な 0 を入力するとエラーに
% なります。
%
% 2. MATLAB のコマンドラインから直接操作する場合には、操作するご
% とに figure数が増えていきます。適宜、消去操作を行ってください。
%
% 3. [座標面],[余白],[紙面全面]は新しく呼び出されたものが最前面に
% 配置されます。見せるべき面が隠れてしまった場合には、その面を再
% 呼び出しすれば見えるようになります。
%
% 4. このfunctionは、一つのプログラムの中から何回でも呼び出して複
% 数のfigureページを作ることができます。しかし、呼び出すたびに、
% 前回のfigure上の[座標面]へのハンドルは失われますので、遡っての
% 編集はできなくなりなります。必ず、1枚ごとに完璧に仕上げてから、
% 次の呼び出しに移ってください。
% ==================
% 作成者 :tsubolabo
% 年月日 :2022-12/03
% 使用Version :MATLAB R2019a Home
% 文字code :Shift-JIS
% 利用制限 :なし
% 賠償責任 :負いません(#^^#)
% ==================
% === 用紙の呼称と寸法の対応表
size_table={'A3' [297 420];
'B4' [257 364];
'A4' [210 297];
'B5' [182 257];
'A5' [149 210]};
% === 指定された用紙の向きを考慮して、用紙の幅と高さを設定。
n=find(strcmp(pp_size,{size_table{:,1}})); % 指定用紙は対応表のn行目
dim=size_table{n,2}; % 指定用紙の [ 短辺 長辺 ] を取得。
if orient=='land'
dim=fliplr(dim); % 用紙の向きが横のときは、幅と高さを入れ替え
% ここで、dim = [ 幅 高さ ] に変わる。
end
width_pp =dim(1); % 用紙幅
height_pp=dim(2); % 用紙高さ
% === [mm] → [normalized](figureの全幅,全高が1.0) への換算係数
Kh=1/height_pp; % 縦方向の [mm] → [normalized] 換算係数
Kw=1/width_pp; % 横方向の 〃
% === [座標面]間の隙間[mm]
if struct(2)~=1 % 2列以上の構成のとき
Gw=(width_pp-margin(3)-margin(4) ...
-struct(2)*ax_size(1))/(struct(2)-1);
% [座標面]間の横方向の隙間
else % 1列だけの構成のとき
Gw=0;
margin(4)=width_pp-margin(3)-ax_size(1); % 右余白幅を強制書き替え
end
if struct(1)~=1 % 2行以上の構成のとき
Gh=(height_pp-margin(1)-margin(2) ...
-struct(1)*ax_size(2))/(struct(1)-1);
% [座標面]間の高さ方向の隙間
else % 1行だけの構成のとき
Gh=0;
margin(1)=height_pp-margin(2)-ax_size(2); % 上余白高を強制書き替え
end
% === 各領域(余白,座標面,隙間) が占有する幅[mm]の並び(左から右の順)
Wp=[margin(3) ax_size(1) ...
repmat([Gw ax_size(1)],1,struct(2)-1) margin(4)];
% === 各領域が占有する高さ[mm]の並び(下から上の順)
Hp=[margin(2) ax_size(2) ...
repmat([Gh ax_size(2)],1,struct(1)-1) margin(1)];
% === 各[座標面]の左下隅の座標を計算
Int_Wp=conv(Wp,ones(1,length(Wp))); % Wpを左から積算
Pw=Int_Wp(1:2:length(Wp)-1);
% 各[座標面]左端の、用紙左端からの位置[mm]
Int_Hp=conv(Hp,ones(1,length(Hp))); % Hpを下から積算
Ph=Int_Hp(1:2:length(Hp)-1);
% 各[座標面]下端の、用紙下端からの位置[mm]
% === バソコンのスクリーンサイズの取得
s_size=get(0,'ScreenSize'); % [left bottom width height] [pixel]。
% left,bottomは常に1。
% === 下記の幅を考慮し、表示可能な最大のfigureサイズ[pixel]を割り出す
%
% このサイズは、Figure のツールバー類や枠を除いた純粋な正味のサイズ。
% ただし、Windows10, R2019a の場合なので、他の環境では合わないかも。
%
% windows画面下のタスクバーの幅 = 33[pixel]
% windows画面右のタスクバーの幅 = 62[pixel]
% figure window 上下左右の枠幅 = 0[pixel]
% figure window 上部のツールバー類の幅(除:上枠) = 79[pixel]
taskb=33+2; taskr=62+2; frame=0; tool=79+2;
% +2 の余裕を持たせて、figure窓の外縁が隠れない程度に補正。
h_max=s_size(4)-taskb-tool-2*frame; % 表示可能な縦方向の最大長[pixel]
w_max=s_size(3)-2*frame-taskr; % 表示可能な横方向の最大長[pixel]
% === 用紙と画面のアスペクト比に応じてfigureの位置決め
if h_max/w_max>height_pp/width_pp % 用紙の方が画面よりも横長のとき
% 幅優先の割り付け
posy=s_size(4)-w_max*height_pp/width_pp-tool-2*frame;
% figure の下端を置くべき位置
figure('Position', ...
[1 posy w_max w_max*height_pp/width_pp],'Resize','off');
% 画面上端に接して、有効幅いっぱいに配置
else
% 高さ優先の割り付け
posx=s_size(3)-h_max*width_pp/height_pp-taskr-2*frame;
% figure の左端を置くべき位置
figure('Position', ...
[posx taskb h_max*width_pp/height_pp h_max],'Resize','off');
% 右タスクバーに接して、有効高さいっぱいに配置
end
% === 各[座標面]へのハンドル hax(1)~hax([座標面]数)(関数の出力)
Nax=struct(1)*struct(2);
Mpos=zeros(Nax,4); % [座標面]のPosition情報(下記)を入れる行列。
% 各行は、[ 左下隅のx座標 同y座標 幅 高さ ]
% これが、[座標面]番号順に縦に並ぶ。
% 単位は[normalized]
hax=zeros(1,Nax); % サイズの事前割り付け(必須に非ず。警告回避用)
for N=1:struct(1) % 上から数えた[座標面]の行番号
for M=1:struct(2) % 左から数えた[座標面]の列番号
na=(N-1)*struct(2)+M; % [座標面]番号
each_pos=[Pw(M)*Kw Ph(struct(1)+1-N)*Kh ...
ax_size(1)*Kw ax_size(2)*Kh];
% [座標面]の[左下隅x,y,幅,高さ] [normalized]
hax(na)=axes('Position',each_pos); % [座標面]の設定
Mpos(na,:)=each_pos;
end
end
% === 上余白へのハンドル hsp(1)(関数の出力)
hsp=zeros(1,6);
% [座標面]群全体に外接する長方形の大きさ
width_box =width_pp-margin(3)-margin(4);
height_box=height_pp-margin(1)-margin(2);
hsp(1)=axes('Position', ...
[0*Kw (height_pp-margin(1))*Kh width_pp*Kw margin(1)*Kh]);
% 上余白内の座標の原点は下端中央とし、単位は[mm]とする。
xlim([-margin(3)-width_box/2 width_box/2+margin(4)]);
ylim([0 margin(1)]);
hold on % 軸スケールを固定
grid on
set(gca,'Color','none'); % 余白面の背景を透明化。
% 一時的に axis on にしたとき、隣接する
% [座標面]のタイトルなどを隠さないため。
axis off % 座標軸は非表示とする。
% === 下余白へのハンドル hsp(2)(関数の出力)
hsp(2)=axes('Position',[0*Kw 0*Kh width_pp*Kw margin(2)*Kh]);
% 下余白内の座標の原点は上端中央とし、単位は[mm]とする。
xlim([-margin(3)-width_box/2 width_box/2+margin(4)]);
ylim([-margin(2) 0]);
hold on
grid on
set(gca,'Color','none');
axis off
% === 左余白へのハンドル hsp(3)(関数の出力)
hsp(3)=axes('Position',[0*Kw 0*Kh margin(3)*Kw height_pp*Kh]);
% 左余白内の座標の原点は右端中央とし、単位は[mm]とする。
xlim([-margin(3) 0]);
ylim([-margin(2)-height_box/2 height_box/2+margin(1)]);
hold on
grid on
set(gca,'Color','none');
axis off
% === 右余白へのハンドル hsp(4)(関数の出力)
hsp(4)=axes('Position', ...
[(width_pp-margin(4))*Kw 0*Kh margin(4)*Kw height_pp*Kh]);
% 右余白内の座標の原点は左端中央とし、単位は[mm]とする。
xlim([0 margin(4)]);
ylim([-margin(2)-height_box/2 height_box/2+margin(1)]);
hold on
grid on
set(gca,'Color','none');
axis off
% === 紙面全体へのハンドル([mm]用) hsp(5)(関数の出力)
hsp(5)=axes('Position',[0*Kw 0*Kh width_pp*Kw height_pp*Kh]);
% 紙面全体のこの座標の原点は左下とし、単位は[mm]とする。
xlim([0 width_pp]);
ylim([0 height_pp]);
hold on
grid on
set(gca,'Color','none');
axis off
% === 紙面全体へのハンドル([normalized]用) hsp(6)(関数の出力)
hsp(6)=axes('Position',[0 0 1.0 1.0]);
% 紙面全体のこの座標の原点は左下とし、単位は[normalized]とする。
xlim([0 1.0]);
ylim([0 1.0]);
hold on
grid on
set(gca,'Color','none');
axis off
% === [座標面]のサイズの指定が大き過ぎて重なり合ってしまったとき、図の
% 境界を見失うのを防ぐために、各[座標面]の手前・背後の表示関係を整
% え直す。
if Gh<0 % 高さ方向の隙間がマイナスになって[座標面]が重なるとき
for N=struct(1):-1:1 % 上から数えた[座標面]の行番号
for M=1:struct(2) % 左から数えた[座標面]の列番号
axes(hax(M+(N-1)*struct(2)));
end
end
end
% === 呼び出しに第6引数 Mcomb が与えられている場合。
% グループ化処理で[座標面]の再編成を行う
if nargin==6
Nx=struct(2); % [座標面]群の列数
Ny=struct(1); % 〃 行数
Wax=ax_size(1)*Kw; % [座標面]の幅 [normalized]
Hax=ax_size(2)*Kh; % 〃 の高さ[normalized]
% === Mcomb の指定値が適正かどうかを判定する。
%
% 左上隅 右下隅
% 行 列 行 列
% Mcomb = [ L1a C1a L2a C2a ] --- aグループ
% [ L1b C1b L2b C2b ] --- bグループ
% [ L1c C1c L2c C2c ] --- cグループ
% [ ............... ]
%
% 適正とは:
% 存在しない[座標面]が指定されていないか?
% グループ領域指定順序が左上→右下になっているか?
% 同一[座標面]が重複して指定されていないか?
% [座標面]が一つだけのグループはないか?
% === 存在しない[座標面]が指定されていないか?
% 1<(L1,L2)<Ny 1<(C1,C2)<Nx であればOK。
msg='指定グループ内に、存在しない[座標面]が含まれています';
LL=[Mcomb(:,1)' Mcomb(:,3)'];
CC=[Mcomb(:,2)' Mcomb(:,4)'];
judge1=find(LL<1|LL>Ny); % empty なら問題なし
judge2=find(CC<1|CC>Nx);
if isempty(judge1)
if isempty(judge2)
% 条件クリア
else
error(msg)
end
else
error(msg)
end
% === グループ領域指定順序が左上→右下になっているか?
% L2>=L1, C2>=C1 → L2-L1>=0, C2-C1>=0 であればOK。
msg='グループ領域の指定順序は左上→右下にしてください';
LL=Mcomb(:,3)'-Mcomb(:,1)';
CC=Mcomb(:,4)'-Mcomb(:,2)';
judge1=find(LL<0); % empty なら問題なし
judge2=find(CC<0);
if isempty(judge1)
if isempty(judge2)
% 条件クリア
else
error(msg)
end
else
error(msg)
end
% === [L1 C1 L2 C2]表現のグループを、[座標面]番号のグループに変換。
Ngroup=size(Mcomb,1); % グループの数
Group={}; % [座標面]番号のベクトルで表示したグループを
% グループ数だけ縦に重ねたセルの配列
for n=1:Ngroup
gr=[]; % 1つのグループの[座標面]番号のベクトル
for m=Mcomb(n,1):Mcomb(n,3) % グループを行方向にスキャン
for i=Mcomb(n,2):Mcomb(n,4) % 〃 列方向 〃
gr=[gr (m-1)*Nx+i];
end
end
Group=[Group; gr];
end
% === [座標面]が一つだけのグループはないか?
% length(Group{?})>1 であればOK。
msg='グループ内の[座標面]は2つ以上にしてください';
for n=1:Ngroup
if length(Group{n})==1
error(msg)
end
end
% === 同一[座標面]が重複して指定されていないか?
msg='複数のグループで共有している[座標面]があります';
axes_xx=[]; % グループ要素に指定された全[座標面]番号を
% 列挙した行ベクトル。
for n=1:Ngroup
axes_xx=[axes_xx Group{n}];
end
axes_xx=sort(axes_xx); % 昇順に並べ直す
axes_xxs=circshift(axes_xx,1); % 右に循環シフト
judge=find((axes_xx-axes_xxs)==0); % 同一番号の並びがあれば答あり。
if isempty(judge) % 答がなかったとき。
% 条件クリア
else
error(msg)
end
% ======== ここで、Mcomb の入力値の適否の判定は完了 ========
% この段階で、axes_xxには、統合される[座標面]番号が昇順に並んでいる。
% === [座標面]のグループ化の本格処理に入る。
Mpos=[Mpos; zeros(Ngroup,4)]; % 既製[座標面]のPosition情報の下に
% 新製の大[座標面]の情報も追加する
for n=1:Ngroup
L1=Mcomb(n,1); % グループの左上の[座標面]の行番号
C1=Mcomb(n,2); % 〃 列番号
L2=Mcomb(n,3); % グループの右下の[座標面]の行番号
C2=Mcomb(n,4); % 〃 列番号
nax=(L2-1)*Nx+C1; % グループの左下にある[座標面]番号
Ax=Mpos(nax,1); % その[座標面]の左下隅の座標値Ax,Ay。
Ay=Mpos(nax,2);
WW=(C2-C1+1)*Wax+(C2-C1)*Gw*Kw; % 統合後の大[座標面]の幅と高さ
HH=(L2-L1+1)*Hax+(L2-L1)*Gh*Kh;
Mpos(Nax+n,:)=[Ax,Ay,WW,HH];
end
Mpos(axes_xx,:)=[]; % 統合で消滅した[座標面]のPosition情報行は削除
Mpos=[Mpos round(Mpos(:,2)+Mpos(:,4),4)];
% 横書き文書の読み書き順にソートするため、
% 5列目に[座標面]上端の縦座標値を追加。
% 微妙な計算誤差を避けるため値は丸める。
Mpos=sortrows(Mpos,[5 1],{'descend' 'ascend'});
% 5列目を降順、1列目を昇順にソート。
Mpos(:,5)=[]; % 不要になった5列目を削除。
for n=1:Nax
axes(hax(n)); % 一旦、余白以外の[座標面]をハンドルごと削除。
delete(gca)
end
Naxa=size(Mpos,1); % 統合後の全[座標面]数
% === [座標面]を再設定。
for n=1:Naxa
hax(n)=axes('Position',[Mpos(n,1) Mpos(n,2) Mpos(n,3) Mpos(n,4)]);
end
end % =============== end of [if nargin==6](グループ化処理の終了)
Naxa=size(Mpos,1); % 統合後の全[座標面]数。
% [if nargin==6]でないときは未定義なので再設定。
% === [座標面]や[余白]のハンドル名を表示
% [座標面]
txtx=[];
txty=[];
txtc={};
for n=1:Naxa
txtx=[txtx ; Mpos(n,1)+Mpos(n,3)/2]; % 位置のx,y座標値
txty=[txty ; Mpos(n,2)+Mpos(n,4)/2];
txtc=[txtc ; ['hax (' num2str(n) ')']]; % ハンドル名
end
% 上余白
txtx=[txtx ; 0.5];
txty=[txty ; (height_pp-margin(1)/2)*Kh];
txtc=[txtc ; 'hsp (1)'];
% 下余白
txtx=[txtx ; 0.5];
txty=[txty ; (margin(2)/2)*Kh];
txtc=[txtc ; 'hsp (2)'];
% 左余白
txtx=[txtx ; (margin(3)/2)*Kw];
txty=[txty ; 0.5];
txtc=[txtc ; 'hsp (3)'];
% 右余白
txtx=[txtx ; (width_pp-margin(4)/2)*Kw];
txty=[txty ; 0.5];
txtc=[txtc ; 'hsp (4)'];
% 紙面全体(2種類)
txtx=[txtx ; 0.93];
txty=[txty ; 0.93];
txtc=[txtc ; 'hsp (5) [mm]'];
txtx=[txtx ; 0.93];
txty=[txty ; 0.88];
txtc=[txtc ; 'hsp (6) [norm]'];
axes(hsp(6));
h_number=text(txtx,txty,txtc,'Rotation',45, ...
'HorizontalAlignment','center','FontSize',12);
for n=Naxa+1:Naxa+6
h_number(n).Color='[0 0 1]';
end
h_number(Naxa+7)=text(0.02,0.97, ...
'座標ハンドル名は delete(h\_number) で消去します。', ...
'HorizontalAlignment','left','FontSize',16,'Color','red');
end % end of function 'make_axes_tidily'
% ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
% 以下には、本functionの使用例を示すプログラムをコメント化して掲載し
% ています。
% '% % test_for_make_axes_tidily.m' 以下の全行をコピーし、全行頭の
% '% 'の2文字を削除してから、適当なmファイル名で保存して実行させてみて
% ください( Editorの文字のEncodeの種類は、MATLABのコマンドラインから
% 'slCharacterEncoding()'として調べ、それに合わせます)。
% ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
%
% % test_for_make_axes_tidily.m
%
% clear
% close all
%
% % [座標面]生成関数の呼び出し(用紙1枚目) ======================
% [hax,hsp,h_number]=make_axes_tidily( ...
% 'A4','land',[4 6],[41.5 38],[30 10 25 25]);
% % =============================================================
%
% delete(h_number); % [座標面]ハンドル番号表示の消去
%
% [X,Y,Z]=peaks(20);
%
% axes(hax(1)); surf(X,Y,Z); title('surf'); label_off;
% axes(hax(2)); h=surf(X,Y,Z); h.EdgeColor='none'; ...
% title('surf (edge color: none)'); label_off;
% axes(hax(3)); surfl(X,Y,Z); title('surfl');label_off;
% axes(hax(4)); mesh(X,Y,Z); title('mesh');label_off;
% axes(hax(5)); meshc(X,Y,Z); title('meshc');label_off;
% axes(hax(6)); meshz(X,Y,Z); title('meshz');label_off;
% axes(hax(7)); waterfall(X,Y,Z); title('waterfall');label_off;
% axes(hax(8)); plot3(X,Y,Z); title('plot3'); grid on; label_off;
% axes(hax(9)); imagesc(Z); title('imagesc');label_off;
% axes(hax(10)); image(Z); title('image');label_off;
% axes(hax(11)); contour(X,Y,Z); title('contour');label_off;
% axes(hax(12)); contourf(Z); colormap(gca,parula); ...
% title('contourf (parula-default)'); label_off;
% axes(hax(13)); contourf(Z); colormap(gca,hsv); ...
% title('contourf (hsv)'); label_off;
% axes(hax(14)); contourf(Z); colormap(gca,hot); ...
% title('contourf (hot)'); label_off;
% axes(hax(15)); contourf(Z); colormap(gca,cool); ...
% title('contourf (cool)'); label_off;
% axes(hax(16)); contourf(Z); colormap(gca,spring); ...
% title('contourf (spring)'); label_off;
% axes(hax(17)); contourf(Z); colormap(gca,summer); ...
% title('contourf (summer)'); label_off;
% axes(hax(18)); contourf(Z); colormap(gca,autumn); ...
% title('contourf (autumn)'); label_off;
% axes(hax(19)); contourf(Z); colormap(gca,winter); ...
% title('contourf (winter)'); label_off;
% axes(hax(20)); contourf(Z); colormap(gca,gray); ...
% title('contourf (gray)'); label_off;
% axes(hax(21)); contourf(Z); colormap(gca,bone); ...
% title('contourf (bone)'); label_off;
% axes(hax(22)); contourf(Z); colormap(gca,copper); ...
% title('contourf (copper)'); label_off;
% axes(hax(23)); contourf(Z); colormap(gca,pink); ...
% title('contourf (pink)'); label_off;
% axes(hax(24)); contourf(Z); colormap(gca,jet); ...
% title('contourf (jet)'); label_off;
%
% axes(hsp(1));
% text(0,15, ...
% '[X,Y,Z] = peaks(20) のデータを使った各種グラフ表現', ...
% 'FontSize',14,'HorizontalAlignment','center');
%
% % ==========================================================
%
% % [座標面]のグループ化行列の指定
%
% Mcomb=[2 2 3 4
% 1 1 4 1
% 1 5 2 6
% 4 4 4 6];
%
% % [座標面]生成関数の呼び出し(用紙2枚目) ======================
% [hax,hsp,h_number] = make_axes_tidily ...
% ('A4','land',[4 6],[35 30],[35 25 25 25],Mcomb);
% % =============================================================
%
% colb=[0 0.447 0.741]; % 線の色(既定青)
% colr=[0.85 0.325 0.098]; % 線の色(既定赤)
%
% % ===== 二次系・ボード線図 =======================
% axes(hax(6));
%
% x=linspace(-2,2,201);
% gg=linspace(-40,30,12);
% kk=(10.^(-gg/20))/2;
%
% for k=kk
% w=10.^x;
% G=1./(-w.^2+2*k*i*w +1);
% g=20*log10(abs(G));
% a=unwrap(angle(G))*180/pi;
%
% yyaxis left;
% semilogx(w,g,'-','Color',colb);
% grid on
% ylim([-140 40]);
% hold on
% semilogx([1.8 70],[0 0],'-k','Color',[1 1 1]*0.4);
%
% yyaxis right;
% semilogx(w,a,'-','Color',colr);
% semilogx([1 100],[0 0],'-k','Color',[1 1 1]*0.4);
% yticks(-200:40:160);
% ylim([-200 160]);
% end
%
% % ===== 二次系・過渡特性 =========================
% % axes(hax(2→3→4→8));
%
% kk=[0.005 0.05 0.3 1.0];
% ax=[2 3 4 8];
% t=linspace(0,60,101);
%
% for n=1:4
% axes(hax(ax(n))); % axes(hax(2→3→4→8));
% k=kk(n);
% if k==1.0
% k=1.0001; % 特異点回避
% end
%
% [tran]=response(k,t);
% plot(t,tran);
% grid on
% xlim([0 60]);
% ylim([0 2]);
% hold on
% text(58,1.8,['\zeta=' num2str(kk(n))], ...
% 'HorizontalAlignment','right','FontSize',8);
% end
%
% % ===== スミス線図 ===============================
% axes(hax(5));
%
% t=linspace(0,2*pi,501);
% A=0.05:0.05:1;
% rx=(1-A)./A;
% for r=rx
% Z=r/(r+1)+(1/(r+1)).*exp(i*t);
% polarplot(angle(Z),abs(Z),'Color',colb);
% hold on
% end
%
% A=(0.05:0.05:0.95)*pi;
% xx=1./tan(A/2);
%
% for x=[xx -xx]
% Z=1+i./x + (1./x).*exp(i*t);
% polarplot(angle(Z),abs(Z),'Color',colr);
% hold on
% end
% polarplot([0 pi],[1 1],'k');
% polarplot([-pi/2 pi/2],[1 1],'k');
%
% rlim([0 1]);
% rticklabels({''});
% thetaticklabels({''});
% grid off
%
% % ===== 三相誘導電動機の静特性 ===================
% axes(hax(9));
%
% % Vo:定格相電圧[Vrms], Io:定格線電流[Arms]
% % f:定格周波数[Hz], X1,X2,Xm:一次二次励磁リアクタンス[pu]
% % r1,r2:一次二次巻線抵抗[pu], puGD2:GD^2[pu], P:モータ極数
%
% Vo=1; Io=1; f=60; X1=3.1; X2=3.1; Xm=3.0; r1=0.02; r2=0.02;
% puGD2=1; P=2;
%
% [s,Tor,I1,PF,so,L1,L2,M,R1,R2,J] ...
% = motor_static(Vo,Io,f,X1,X2,Xm,r1,r2,puGD2,P);
%
% Toro=interp1(s,Tor,so); % 定格トルク[Nm]
%
% plot(1-s,Tor/Toro);
% hold on
% plot(1-s,abs(I1)/Io);
% plot([0 1],[1 1])
% grid on
%
% % ===== 三相誘導電動機 d,q軸上の直入れ動特性 ====
% axes(hax(10));
%
% t0=2; T_L=Toro; % 始動2秒後、定格負荷トルク印加
%
% [t,y]=ode45(@(t,y) motor_dynamic( ...
% t,y,L1,L2,M,R1,R2,J,P,Vo,f,T_L,t0,0),[0 3],[0 0 0 0 0 0]);
%
% plot([0 t0 t0 3],[0 0 100 100],'Color','[0 0.5 0]')
% hold on
% set(gca,'ColorOrderIndex',1);
% plot(t,[y(:,1) y(:,2)]*10)
% plot(t,y(:,5));
% grid on
% ylim([-200 400]);
% yticklabels({''});
%
% % ===== 三相誘導電動機 直入れ起動の電流波形 =====
% axes(hax(11));
%
% ida=y(:,1).*cos(y(:,6)) - y(:,2).*sin(y(:,6));
% iqa=y(:,1).*sin(y(:,6)) + y(:,2).*cos(y(:,6));
%
% iu=sqrt(2/3)*ida;
% iv=sqrt(2/3)*( (-1/2)*ida + (sqrt(3)/2)*iqa );
% iw=sqrt(2/3)*( (-1/2)*ida - (sqrt(3)/2)*iqa );
%
% plot(t,[iu iv iw]);
% grid on
% xlim([0 0.2]);
% yticklabels({''});
%
% % ===== 三相誘導電動機 低周波起動の電流波形 =====
% axes(hax(1));
%
% % 60Hzまで1.8秒で加速し、2秒で定格負荷トルク印加。
% ff=60; tr=1.8; t0=2;
%
% [t,y]=ode45(@(t,y) motor_dynamic( ...
% t,y,L1,L2,M,R1,R2,J,P,Vo,ff,T_L,t0,tr), ...
% [0 2.5],[0 0 0 0 0 0]);
%
% ida=y(:,1).*cos(y(:,6)) - y(:,2).*sin(y(:,6));
% iqa=y(:,1).*sin(y(:,6)) + y(:,2).*cos(y(:,6));
%
% iu=sqrt(2/3)*ida;
% iv=sqrt(2/3)*( (-1/2)*ida + (sqrt(3)/2)*iqa );
% iw=sqrt(2/3)*( (-1/2)*ida - (sqrt(3)/2)*iqa );
%
% plot([iu iv iw],t);
% grid on
% ylim([0 2.5]);
% xticklabels({''});
% yticklabels({''});
%
% % ===== 空座標 ===================================
% axes(hax(7));
%
% axis off
%
% axes(hsp(1));
% text(0,12, ...
% 'モータ特性、ボード線図、スミス線図 など グラフ色々', ...
% 'FontSize',14,'HorizontalAlignment','center');
%
% % ===== [座標面]ハンドル番号表示の消去 =============
% delete(h_number);
%
% % ===== 同等の subplot の画面を参考表示 ====================
%
% figure(3)
% for n=1:24
% subplot(4,6,n);
% end
%
% subplot(4,6,[1 7 13 19]);
% text(2.4,1.05,'MATLAB標準の subplot','FontSize',12);
% subplot(4,6,[5 6 11 12]);
% subplot(4,6,[8 9 10 14 15 16]);
% subplot(4,6,[22 23 24]);
%
% % ==========================================================
%
% function label_off % 軸ラベルの3軸一括消去のための関数
% xticklabels({''});
% yticklabels({''});
% zticklabels({''});
% end
%
% % ==========================================================
%
% function [tran]=response(k,t) % 二次系のステップ応答
% if k>1 % 非振動系
% k2=sqrt(k^2-1);
% k3=-k+k2;
% k4=-k-k2;
% tran = exp(k3*t)/(2*k2*k3) - exp(k4*t)/(2*k2*k4) + 1;
% else % 振動系
% w=sqrt(1-k^2);
% p=atan2(k,w);
% tran = 1 - cos(w*t-p).*exp(-k*t)/w;
% end
% end
%
% % ==========================================================
%
% % 三相誘導電動機の静特性
% function [s,Tor,I1,PF,so,L1,L2,M,R1,R2,J] ...
% = motor_static(Vo,Io,f,X1,X2,Xm,r1,r2,puGD2,P)
%
% Wo=2*pi*f; Wr=linspace(0,1,2001)*Wo; s=1-Wr/Wo; Zo=Vo/Io;
% L1=X1*Zo/Wo; L2=X2*Zo/Wo; M=Xm*Zo/Wo; R1=r1*Zo; R2=r2*Zo;
%
% D1=R1+i*Wo*L1; D2=(R2./s)+i*Wo*L2; D=D1*D2+(Wo*M)^2;
% I1=((R2./s)+i*Wo*L2)*Vo./D; I1(end)=Vo/(R1+i*Wo*L1);
% I2=i*Wo*M*Vo./D; I2(end)=0;
%
% PF=cos(angle(I1))*100; Pow=3*R2*((1-s)./s).*(abs(I2).^2);
% Wm=2*Wr/P; Tor=Pow./Wm; Tor(end)=0;
% Wro=interp1(abs(I1),Wr,Io); I2o=interp1(Wr,abs(I2),Wro);
% so=1-Wro/Wo; Powo=3*R2*((1-so)/so)*(I2o^2); Wmo=2*Wro/P;
% Toro=Powo/Wmo; J=puGD2*Toro/Wmo;
%
% end
%
% % ==========================================================
%
% % 三相誘導電動機の動特性(ode45用)
% function dydt= ...
% motor_dynamic(t,y,L1,L2,M,R1,R2,J,P,Voo,ff,T_L,t0,tr)
%
% % isd,isq: d軸q軸固定子電流[A]
% % prd,prq: d軸q軸回転子鎖交磁束数[Wb]
% % Wr: モータ電気速度[rad/s]
% % y(6): 積算電気角θ(外部で使用)[rad]
%
% isd=y(1); isq=y(2); prd=y(3); prq=y(4); Wr=y(5)*P/2;
%
% if t<tr
% f=ff*(t/tr);
% Vo=Voo*t/tr;
% Vo=min([Vo Voo*(t/(0.3*tr))^2 ]);
% Vo=max([Vo 0.04*Voo]);
% else
% f=ff;
% Vo=Voo;
% end
%
% Vsd=sqrt(3)*Vo; Vsq=0; Wo=2*pi*f;
% A=zeros(6,6); B=zeros(6,4);
% q=1-M^2/(L1*L2);
% A(1,1)=-( R1/(q*L1)+R2*M^2/(q*L1*L2^2)); A(1,2)=Wo;
% A(1,3)=R2*M/(q*L1*L2^2); A(1,4)=Wr*M/(q*L1*L2); A(2,1)=-Wo;
% A(2,2)=A(1,1); A(2,3)=-A(1,4); A(2,4)=A(1,3); A(3,1)=R2*M/L2;
% A(3,3)=-R2/L2; A(3,4)=Wo-Wr; A(4,2)=A(3,1); A(4,3)=-A(3,4);
% A(4,4)=A(3,3); a=P^2*M/(4*J*L2); A(5,1)=-a*prq; A(5,2)=a*prd;
% B(1,1)=1/(q*L1); B(2,2)=B(1,1); B(5,3)=-P/(2*J); B(6,4)=2*pi;
%
% Ts=0;
% if t>=t0
% Ts=T_L; % 負荷トルク
% end
%
% dydt = A*y + B*[Vsd Vsq Ts f]';
%
% end
%
% % ==========================================================
プログラム freely版
function [hax,hsp,h_number] = make_axes_freely ...
(pp_size, orient, Maxes)
%
% =======================
% make_axes_freely ヘルプ
% =======================
%
% =====
% 概要:
% =====
%
% 一枚の規格用紙を想定した画面上に、任意の位置と大きさを持つ複数の
% [座標面]を生成します。位置や大きさの指定は、規格用紙上の[mm]単位で
% 行えます。前もって、規格用紙にスケッチして、グラフ類のレイアウトを
% デザインするような使い方をするときに便利です。
%
% このプログラムの末尾には、利用例のプログラムをコメント化して添付
% しています。
%
% =====
% 特徴:
% =====
%
% 組み込みの subplot コマンドで複数の[座標面]を作っても、レイアウ
% ト上の制限が大きく、あまり自由な表現はできません。もう一つのユーザ
% ー定義関数 make_axes_tidily によれば、ある程度、自由度は上げられま
% す。しかし、それでも対応できないような場合には、これを使うことで解
% 決できます。
%
% =====
% 呼び出し形式:
% =====
%
% [hax,hsp,h_number] = make_axes_freely(pp_size, orient, Maxes);
%
% =====
% 入力:
% =====
%
% pp_size: 印刷用紙のサイズ
% 'A3' = 297 * 420 [mm] ( 短辺 * 長辺 )
% 'B4' = 257 * 364 [mm]
% 'A4' = 210 * 297 [mm]
% 'B5' = 182 * 257 [mm]
% 'A5' = 149 * 210 [mm]
%
% orient: 印刷用紙の向き
% 'port' = 縦(portrait)
% 'land' = 横(landscape)
%
% Maxes: [座標面]の位置と大きさを指定した行ベクトルを、
% [座標面]の数だけ縦に並べて作った行列。
% [ X1 Y1 W1 H1 ]
% [ X2 Y2 W2 H2 ]
% [ X3 Y3 W3 H3 ]
% [ : : : : ]
% [ : : : : ]
% ただし、
% X: [座標面]左下隅の、用紙左端からの寸法[mm]
% Y: 〃 用紙下端からの寸法[mm]
% W: [座標面]の幅[mm]
% H: 〃 高さ[mm]
%
% =====
% 出力:
% =====
%
% hax: 各[座標面]へアクセスするためのハンドル
% hax(1), hax(2), ..., hax([座標面]の全数)
% ( )内のハンドル番号は、入力の Maxes 行列の指定行番に同
% じ。
%
% hsp: 用紙上の、[座標面]が設定されていない上下左右の余白部分も、
% 文字などを書き込むための領域として利用できる。これらの各
% 余白領域や紙面全領域へアクセスするためのハンドルである。
% なお、これら全領域とも、axis off に設定しているので軸は
% 表示されない。
% 領域内の原点
% hsp(1): 上余白 下端中央
% hsp(2): 下余白 上端中央
% hsp(3): 左余白 右端中央
% hsp(4): 右余白 左端中央
% hsp(5): 紙面全面 左下隅
% 以上、領域内での位置指定単位は[mm]
% hsp(6): 紙面全面 左下隅
% これだけは、領域内での位置指定単位は[normalized]
% legend などは normalized での位置指定が必要なため
%
% h_number: 初期画面に[座標面]へのハンドル名が表示されるが、これを消
% 去するためのハンドル。消去するには delete(h_number) と指
% 示する。
%
% ==========
% 使用方法:
% ==========
%
% 予め、規格サイズの用紙上に、グラフ全体の大まかなイメージをスケッチ
% しておきます。この図からそれぞれの座標面の位置や大きさを[mm]単位で
% 読み取り、入力用の Maxes 行列を作ります。[座標面]同士が重なろうが、
% 用紙の一方に片寄ろうが、お構いなしの自由度です。
% 例:
% Maxes = [ 37 45 28 120
% 67 115 50 50
% 67 45 25 40
% 212 45 45 120
% 147 145 70 20
% 97 45 100 80
% 157 75 60 30 ];
%
% MATLAB のコマンドラインからでも、プログラムからでも、Maxes 行列を
% 書き込んだあとに、
% [hax,hsp,h_number] = make_axes_freely('A4','land',Maxes);
% などと入力して呼び出します。
%
% すると、すぐに、指定どおりに[座標面]が表示されます。期待どおりの
% イメージになるまで、Maxes の各値の調整を繰り返します。
%
% レイアウトが決まったら、描画したい[座標面]を axes(hax(1)) 等で呼
% び出してから、普通の plot, mesh, text コマンドなどで描画します。
%
% なお、初期画面には、各[座標面]へのハンドル名が表示されています。
% 不要になった段階で、delete(h_number) で消去してください。
%
% 用紙への印刷は、[ファイル]-[印刷プレビュー]画面で、[用紙形式]と
% [印刷の向き]を入力の第1,第2引数に一致するように選択し、[配置]を
% [手動設定のサイズと位置を使用]として、[左]と[上]を0、[幅]と[高さ]
% を[用紙]の値と合わせてから行ってください。
%
% なお、画面上ではタイトルや目盛数値が思い通りに表示されているのに、
% 印刷してみると隣の[座標面]と重なったりすることもあります。印刷結果
% を重視する場合には、文字仕様などの再調整が必要なこともあります。
%
% =====
% 注意:
% =====
%
% 1. MATLAB のコマンドラインから直接操作する場合には、操作するご
% とに figure数が増えていきます。適宜、消去操作を行ってください。
%
% 2. [座標面],[余白],[紙面全面]は新しく呼び出されたものが最前面に
% 配置されます。見せるべき面が隠れてしまった場合には、その面を再
% 呼び出しすれば見えるようになります。
%
% 3. このfunctionは、一つのプログラムの中から何回でも呼び出して複
% 数のfigureページを作ることができます。しかし、呼び出すたびに、
% 前回のfigure上の[座標面]へのハンドルは失われますので、遡っての
% 編集はできなくなりなります。必ず、1枚ごとに完璧に仕上げてから、
% 次の呼び出しに移ってください。
% ==================
% 作成者 :tsubolabo
% 年月日 :2022-12/03
% 使用Version :MATLAB R2019a Home
% 文字code :Shift-JIS
% 利用制限 :なし
% 賠償責任 :負いません(#^^#)
% ==================
% === 用紙の呼称と寸法の対応表
size_table={'A3' [297 420];
'B4' [257 364];
'A4' [210 297];
'B5' [182 257];
'A5' [149 210]};
% === 指定された用紙の向きを考慮して、用紙の幅と高さを設定。
n=find(strcmp(pp_size,{size_table{:,1}})); % 指定用紙は対応表のn行目
dim=size_table{n,2}; % 指定用紙の [ 短辺 長辺 ] を取得。
if orient=='land'
dim=fliplr(dim); % 用紙の向きが横のときは、幅と高さを入れ替え
% ここで、dim = [ 幅 高さ ] に変わる。
end
width_pp =dim(1); % 用紙幅
height_pp=dim(2); % 用紙高さ
% === [mm] → [normalized](figureの全幅,全高が1.0) への換算係数
Kh=1/height_pp; % 縦方向の [mm] → [normalized] 換算係数
Kw=1/width_pp; % 横方向の 〃
% === バソコンのスクリーンサイズの取得
s_size=get(0,'ScreenSize'); % [left bottom width height] [pixel]。
% left,bottomは常に1。
% === 下記の幅を考慮し、表示可能な最大のfigureサイズ[pixel]を割り出す
%
% このサイズは、Figure のツールバー類や枠を除いた純粋な正味のサイズ。
% ただし、Windows10, R2019a の場合なので、他の環境では合わないかも。
%
% windows画面下のタスクバーの幅 = 33[pixel]
% windows画面右のタスクバーの幅 = 62[pixel]
% figure window 上下左右の枠幅 = 0[pixel]
% figure window 上部のツールバー類の幅(除:上枠) = 79[pixel]
taskb=33+2; taskr=62+2; frame=0; tool=79+2;
% +2 の余裕を持たせて、figure窓の外縁が隠れない程度に補正。
h_max=s_size(4)-taskb-tool-2*frame; % 表示可能な縦方向の最大長[pixel]
w_max=s_size(3)-2*frame-taskr; % 表示可能な横方向の最大長[pixel]
% === 用紙と画面のアスペクト比に応じてfigureの位置決め
if h_max/w_max>height_pp/width_pp % 用紙の方が画面よりも横長のとき
% 幅優先の割り付け
posy=s_size(4)-w_max*height_pp/width_pp-tool-2*frame;
% figure の下端を置くべき位置
figure('Position', ...
[1 posy w_max w_max*height_pp/width_pp],'Resize','off');
% 画面上端に接して、有効幅いっぱいに配置
else
% 高さ優先の割り付け
posx=s_size(3)-h_max*width_pp/height_pp-taskr-2*frame;
% figure の左端を置くべき位置
figure('Position', ...
[posx taskb h_max*width_pp/height_pp h_max],'Resize','off');
% 右タスクバーに接して、有効高さいっぱいに配置
end
% === 各[座標面]へのハンドル hax(1)~hax([座標面]数)(関数の出力)
Nax=size(Maxes,1); % [座標面]数
% 入力された[mm]単位の[座標面]情報を[normalized]単位に換算する。
Mpos=[Maxes(:,1)*Kw Maxes(:,2)*Kh Maxes(:,3)*Kw Maxes(:,4)*Kh];
for na=1:Nax
hax(na)=axes('Position',Mpos(na,:));; % [座標面]の設定
end
%=====================================================
% [座標面]群の周囲にできる用紙の余白を計算。
margin(1)=height_pp-max(Maxes(:,2)+Maxes(:,4)); % 上余白[mm]
margin(2)=min(Maxes(:,2)); % 下余白[mm]
margin(3)=min(Maxes(:,1)); % 左余白[mm]
margin(4)=width_pp-max(Maxes(:,1)+Maxes(:,3)); % 右余白[mm]
% [座標面]群全体に外接する長方形の大きさ
width_box =width_pp-margin(3)-margin(4);
height_box=height_pp-margin(1)-margin(2);
hsp=zeros(1,6);
% === 上余白へのハンドル hsp(1)(関数の出力)
hsp(1)=axes('Position', ...
[0*Kw (height_pp-margin(1))*Kh width_pp*Kw margin(1)*Kh]);
% 上余白内の座標の原点は下端中央とし、単位は[mm]とする。
xlim([-margin(3)-width_box/2 width_box/2+margin(4)]);
ylim([0 margin(1)]);
hold on % 軸スケールを固定
grid on
set(gca,'Color','none'); % 余白面の背景を透明化。
% 一時的に axis on にしたとき、隣接する
% [座標面]のタイトルなどを隠さないため。
axis off % 座標軸は非表示とする。
% === 下余白へのハンドル hsp(2)(関数の出力)
hsp(2)=axes('Position',[0*Kw 0*Kh width_pp*Kw margin(2)*Kh]);
% 下余白内の座標の原点は上端中央とし、単位は[mm]とする。
xlim([-margin(3)-width_box/2 width_box/2+margin(4)]);
ylim([-margin(2) 0]);
hold on
grid on
set(gca,'Color','none');
axis off
% === 左余白へのハンドル hsp(3)(関数の出力)
hsp(3)=axes('Position',[0*Kw 0*Kh margin(3)*Kw height_pp*Kh]);
% 左余白内の座標の原点は右端中央とし、単位は[mm]とする。
xlim([-margin(3) 0]);
ylim([-margin(2)-height_box/2 height_box/2+margin(1)]);
hold on
grid on
set(gca,'Color','none');
axis off
% === 右余白へのハンドル hsp(4)(関数の出力)
hsp(4)=axes('Position', ...
[(width_pp-margin(4))*Kw 0*Kh margin(4)*Kw height_pp*Kh]);
% 右余白内の座標の原点は左端中央とし、単位は[mm]とする。
xlim([0 margin(4)]);
ylim([-margin(2)-height_box/2 height_box/2+margin(1)]);
hold on
grid on
set(gca,'Color','none');
axis off
% === 紙面全体へのハンドル([mm]用) hsp(5)(関数の出力)
hsp(5)=axes('Position',[0*Kw 0*Kh width_pp*Kw height_pp*Kh]);
% 紙面全体のこの座標の原点は左下とし、単位は[mm]とする。
xlim([0 width_pp]);
ylim([0 height_pp]);
hold on
grid on
set(gca,'Color','none');
axis off
% === 紙面全体へのハンドル([normalized]用) hsp(6)(関数の出力)
hsp(6)=axes('Position',[0 0 1.0 1.0]);
% 紙面全体のこの座標の原点は左下とし、単位は[normalized]とする。
xlim([0 1.0]);
ylim([0 1.0]);
hold on
grid on
set(gca,'Color','none');
axis off
% === [座標面]や[余白]のハンドル名を表示
% 座標面
txtx=[];
txty=[];
txtc={};
for n=1:Nax
txtx=[txtx ; Mpos(n,1)+Mpos(n,3)/2]; % 位置のx,y座標値
txty=[txty ; Mpos(n,2)+Mpos(n,4)/2];
txtc=[txtc ; ['hax (' num2str(n) ')']]; % ハンドル名
end
% 上余白
txtx=[txtx ; 0.5];
txty=[txty ; (height_pp-margin(1)/2)*Kh];
txtc=[txtc ; 'hsp (1)'];
% 下余白
txtx=[txtx ; 0.5];
txty=[txty ; (margin(2)/2)*Kh];
txtc=[txtc ; 'hsp (2)'];
% 左余白
txtx=[txtx ; (margin(3)/2)*Kw];
txty=[txty ; 0.5];
txtc=[txtc ; 'hsp (3)'];
% 右余白
txtx=[txtx ; (width_pp-margin(4)/2)*Kw];
txty=[txty ; 0.5];
txtc=[txtc ; 'hsp (4)'];
% 紙面全体(2種類)
txtx=[txtx ; 0.93];
txty=[txty ; 0.93];
txtc=[txtc ; 'hsp (5) [mm]'];
txtx=[txtx ; 0.93];
txty=[txty ; 0.88];
txtc=[txtc ; 'hsp (6) [norm]'];
axes(hsp(6));
h_number=text(txtx,txty,txtc,'Rotation',45, ...
'HorizontalAlignment','center','FontSize',12);
for n=Nax+1:Nax+6
h_number(n).Color='[0 0 1]';
end
h_number(Nax+7)=text(0.02,0.97, ...
'座標ハンドル名は delete(h\_number) で消去します。', ...
'HorizontalAlignment','left','FontSize',16,'Color','red');
end % end of function 'make_axes_freely'
% ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
% 以下には、本functionの使用例を示すプログラムをコメント化して掲載し
% ています。
% '% % test_for_make_axes_freely.m' 以下の全行をコピーし、全行頭の
% '% 'の2文字を削除してから、適当なmファイル名で保存して実行させてみて
% ください( Editorの文字のEncodeの種類は、MATLABのコマンドラインから
% 'slCharacterEncoding()'として調べ、それに合わせます)。
% ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
%
% % test_for_make_axes_freely.m
%
% clear
% close all
%
% s1=1; % ハートマークの奥行の前後関係の調整用
% s2=0; % +: 奥へ、-: 手前へ
% s3=-0.5;
% s4=0;
%
% % [座標面]の設定行列の作成([mm]単位)
% Maxes=[ 43 30 60 80
% 48-s1 95 20 20
% 78-s2 93 20 20
% 48-s3 30 20 20
% 78-s4 20 20 20
% 108 30 60 80
% 113+s1 95 20 20
% 143+s2 93 20 20
% 113+s3 30 20 20
% 143+s4 20 20 20 ];
%
% % [座標面]生成関数の呼び出し ==============================
% [hax,hsp,h_number] = make_axes_freely('A5','land',Maxes);
% % =======================================================
%
% [X,Y,Z]=bottle; % クラインの壺のデータを呼び出す。
%
% axes(hax(1)) % 左目用の壺の描画
% surf(X,Y,Z);
% xlabel('X')
% ylabel('Y')
% zlabel('Z')
% axis equal; view(-1,62); axis off
%
% axes(hax(6)) % 右目用の壺の描画
% surf(X,Y,Z);
% xlabel('X')
% ylabel('Y')
% zlabel('Z')
% axis equal; view(5,62); axis off
%
% [line, ~]=heart; % ハートマークのデータを呼び出す。
%
% % ハートマークの描画
% for n=[2 3 4 5 7 8 9 10]
% axes(hax(n));
% patch(line(1,:),line(2,:),[1 0.5 0.5],'EdgeColor','r');
% axis off
% end
%
% axes(hax(1)); % [座標面]の重なりの前後関係を整える。
% axes(hax(6));
% axes(hax(4));
% axes(hax(9));
%
% axes(hsp(1)); % 上余白へのタイトルの書き込み。
% text(-33,10,'裸眼立体視(平行法)左目用', ...
% 'HorizontalAlignment','center', ...
% 'FontSize',16,'Color',[0.7 0.7 0.7])
% text(32,10,'裸眼立体視(平行法)右目用', ...
% 'HorizontalAlignment','center', ...
% 'FontSize',16,'Color',[0.7 0.7 0.7])
%
% delete(h_number); % [座標面]ハンドル番号表示の消去
%
% % ===== ハートマーク生成関数 =====================
%
% function [line, r]=heart
%
% r=[ 0 29; 1.7 35; 5 38.9; 10 40; 15 38.8;
% 18.9 34.5; 20 29; 19.5 25; 17 20; 10 11.5
% 5 6; 0 0 ]';
% pp=spline([1:size(r,2)],r);
% yy = ppval(pp, linspace(1,size(r,2),101));
% yy1=[-yy(1,:); yy(2,:)];
% yy1=fliplr(yy1);
% yy1(:,1)=[];
% line=[yy yy1];
%
% end
%
% % ===== クラインの壺の製造関数 ===================
%
% function [X,Y,Z]=bottle
%
% u = linspace(0,2*pi,35);
% v = linspace(0,2*pi,35);
% [U,V] = meshgrid(u,v);
% X = U*0; Z = U*0;
% idu1 = find(U<=pi); idu2 = find(U>pi);
% R = 4 - 2*cos(U);
% X(idu1) = -4*cos(U(idu1)).*(1+sin(U(idu1))) ...
% - R(idu1).*cos(U(idu1)).*cos(V(idu1));
% X(idu2) = -4*cos(U(idu2)).*(1+sin(U(idu2))) ...
% + R(idu2).*cos(V(idu2));
% Y = R.*sin(V);
% Z(idu1) = -14*sin(U(idu1)) ...
% - R(idu1).*sin(U(idu1)).*cos(V(idu1));
% Z(idu2) = -14*sin(U(idu2));
%
% end
%
% % ==========================================================