はじめに
前回の記事でモンテカルロ法による価値推定をおこないました。
今回は方策改善をおこない、OpenAi GymのCartPoleに適用してみました。
(結果は一番下です)
モンテカルロ法による制御
モンテカルロ法でも、動的計画法を用いた価値反復法と同じように、$①方策\piを評価 \rightleftharpoons ②方策\piを改善$、を繰り返していきます。
動的計画法の時は、状態価値関数を用いて$\pi$を評価しましたが、モンテカルロ法の場合は行動価値関数を用いて方策を評価します。なぜなら、モンテカルロ法の場合環境のダイナミクス($P_{ss'}^a$)を使わない(知らない)ので、状態価値関数からでは最適な行動を決定できないからです。行動価値関数を用いれば、状態と行動の組み合わせについて価値が出るので、最適な行動を選ぶことができます。
行動価値関数を用いた方策評価
行動価値関数を用いる場合の方策評価も状態価値関数の方策評価とほとんど同じです。状態価値関数の場合は開始点を状態sとしエピソードを生成させますが、行動価値関数の場合は開始点を状態s、行動aとしてエピソードを生成させます。
行動価値関数を用いた方策改善
状態s、行動aについての価値$Q(s,a)$がわかっているので、各状態について最も価値の高い行動を方策とします。すなわち
$$\pi(s) \leftarrow argmax_a Q(s,a)$$
モンテカルロ法の実装
OpenAI Gym
それでは、モンテカルロ法を実装しましょう。これまでは、問題設定として格子世界(グリッドワールド)を用いていましたが、せっかく制御するので見た目的に面白いものを使います。
そこで、OpenAI Gymを用います。OpenAi Gymには、強化学習に関するさまざまな問題設定が用意されています。インストール方法や使い方は
OpenAI Gym 入門
が参考になりました。
今回はCartPoleを用います。台車の上にポールが連結されており、台車を左右に動かすことでポールが倒れないようにする、という問題設定です。要は小学校の時に、手のひらに傘を乗せて倒れないようにして遊んだアレです。

この問題の状態$s$は
- 台車の位置
- 台車の速度
- ポールの角度
- ポールの角速度
の4種類です。それぞれがある範囲の連続値をとります。
行動$a$は
- 台車を動かす向き(右or左)
の1種類で、右か左の離散値です。
報酬は、棒を立てたまま1ステップ進むごとに+1です。罰則はありません。棒が倒れた時、もしくは200ステップ経過した時に終端状態となります。したがって、1エピソードでの最高得点は200点です。
開始点探査の問題
ここで、モンテカルロ法の制約について触れます。モンテカルロ法では、エピソードを実際に生成し、その経験から価値関数を推定します。全ての状態、行動に対する価値関数を求めるには、状態と価値の組み合わせの全てを(理論上は無限回)経験する必要があります。これはいつも成り立つでしょうか。そうとは言い切れません。
今回解のCartPole問題では、エピソードの開始点は画面中央にポールが垂直に立った状態から始まります。例えば、「どんな状況でも絶対に右に行く」という方策から始めた場合、(もしくは方策改善の途中でそのような状態になった場合)、左に行くことは無くなるため、左側の位置(状態)に関する経験を得ることができなくなってしまいます。
これを避けるため、学習時には方策$\pi$に常に従うのではなく、一定の確率$\epsilon$でランダムな行動をとるようにします。これを**$\epsilon$-greedy**法と呼びます。
数式で表現すると、方策$\pi=(s,a)$から決まる最適な行動を$a^{*}$としたとき、つまり$a^* = argmax_a Q(s,a)$のときに、
\pi(s,a) = \left\{
\begin{array}{ll}
1-\epsilon + \epsilon/|A(s)| & (a = a^*) \\
\epsilon/|A(s)| & (
a \neq a^*)
\end{array}
\right.
とおきます。$|A(s)|$は状態sの時にとりうる行動の総数です。
アルゴリズム
$\epsilon$グリーディ手法のモンテカルロ法制御アルゴリズムを以下に示します。
すべての$s \in S$, $a \in A(s)$に対して初期化:
$Q(s,a) \leftarrow$ 任意の値
$Returns(s,a) \leftarrow$ 空のリスト
$\pi(s,a) \leftarrow$ 任意の方策
繰り返し:
(a) $\pi$を用いてエピソードを1個生成する
(b) エピソード中に出現する各s,aの対について:
$R \leftarrow s,a$ の初回発生後の収益
$R$を$Returns(s,a)$に追加する
$Q(s,a) \leftarrow average(Returns(s,a))$
(c) エピソード中の各sについて;
$a^* \leftarrow argmax_a ,Q(s,a)$
すべての$a \in A(s))$について;
\pi(s,a) = \left\{
\begin{array}{ll}
1-\epsilon + \epsilon/|A(s)| & (a = a^*) \\
\epsilon/|A(s)| & (
a \neq a^*)
\end{array}
\right.
(ちょっと、最後のブロックが右に寄っていますがご容赦ください)
このアルゴリズムにしたがった実装を以下に解説します。コードの全体はgithubにあります。
離散化処理
# 状態空間を次の様に分割
N =5 # N分割
min_list = [-0.2, -2, -0.05, -1] # 下限値
max_list = [0.15, 0.8, 0.025, 0.5] # 上限値
# 状態を離散化
observation, reward, done, info = env.step(action)
s = [np.digitize(observation[i], np.linspace(min_list[i], \
max_list[i], N-1)) for i in range(num_state)]
CartPole問題では状態が連続値をとるため、離散地に(ムリヤリ)変換する必要があります。そのために、numpyのdigitize関数を用います。まず、N区間に分割する場合、numpy linspace関数で
range = np.linspace(min, max, N-1)
とします。N-1になるところに注意してください。値valをこの区間に押し込める場合は
np.digitize(val, range)
区間から外れた値は、端の区間に割り当てられます。コードでは、各状態変数について行いため、内包表記で書いています。
初期状態
done = False
observation = env.reset() # 環境をリセット
# 状態を離散化
s = [np.digitize(observation[i], np.linspace(min_list[i], max_list[i], N-1))\
for i in range(num_state)]
s_list = [] # エピソードの状態履歴
a_list = [] # エピソードの状態履歴
r_list = [] # エピソードの状態履歴
エージェントをenv.reset()で初期化します。返り値である状態をobservationで受けたのち、上述のdigitize関数で離散化した状態sを作ります。後段の処理のために、各ステップでの状態、行動、報酬を履歴として格納しておく一時リストを初期化します。(Returnリストとは別)
エピソード生成
# エピソードを終端までプレイ
while(done == False):
s_list.append(s)
action = np.random.choice([0,1], p = pi[:,s[0],s[1],s[2],s[3]])
a_list.append(action)
#print("action: %d" % action)
observation, reward, done, info = env.step(action)
r_list.append(reward)
# 状態を離散化
s = [np.digitize(observation[i], np.linspace(min_list[i], \
max_list[i], N-1)) for i in range(num_state)]
状態sにおいて、方策$\pi$から行動を決定します。numpy.random.choice関数は、与えられた確率分布にしたがって、配列内の要素を選択する関数で、$\epsilon$グリーディ法を行うために用意しています。$\epsilon=0$の時は、一つの行動の確率が1、その他が0となり、確定的に行動が選ばれます。
env.step()関数で、選ばれた行動を実行し、新しい状態、報酬を得ます。
変数doneはエピソードが終端状態になったときにTrueとなります。終端状態になったら、エピソード生成ループを抜けます。
Q関数の更新
# エピソードの各ステップから終端状態までの報酬をリストに格納
tmp = 0
for i in range(len(s_list))[::-1]: # リストを逆側から検索
tmp += r_list[i]
returns[a_list[i]][s_list[i][0]][s_list[i][1]][s_list[i][2]][s_list[i][3]].append(tmp)
return_list.append(tmp)
print("eps: %.3f, epi#: %d, state: %s, reward: %3d" % (EPSILON, epi, state, tmp))
Q =np.array([[[[[np.mean(returns[a][_s0][_s1][_s2][_s3]) \
for _s3 in range(N)] for _s2 in range(N)] \
for _s1 in range(N)] for _s0 in range(N)] for a in
range(num_action)])
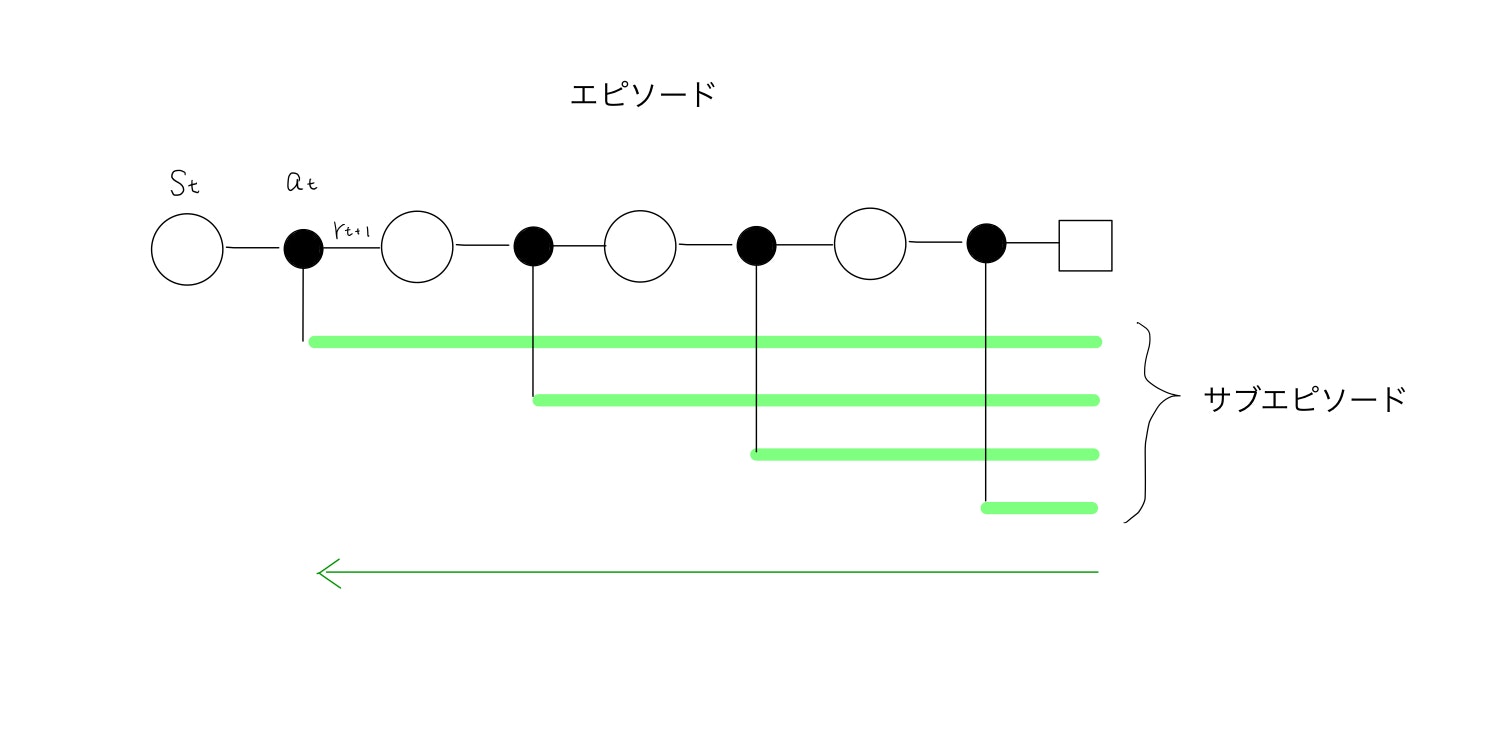
エピソードの履歴は、タイムステップにそってs_list,a_list,r_listに保存されています。下図のように、開始点$s_t$,$a_t$からエピソードを生成し、行動(黒丸)を4回取ったあとに終端状態(四角)に至ったとします。この時、開始点だけでなく、それぞれの途中状態から終端状態に至るエピソードも言わばサブエピソードとしてQ関数更新に用いることができます。逆にこれをせずに、開始点のみを用いると常に同じ状態からスタートすることになり、網羅的な経験を得ることができません。
(注:間違っていたらご指摘ください!!!)
各ステップの状態行動対を、それぞれのサブエピソード(緑の線)の開始点としてReturnに収益を追加していきます。収益はそれぞれのサブエピソードで得た報酬の合計です。各サブエピソードに対して合計を計算していくよりも、履歴を後ろから辿って報酬を足していって途中の計算結果を共有した方が効率が良いため、そうしています。
その後、各状態行動対に対するReturnリストの平均を求め、Qを更新します。Returnリスト(のリスト)の引数指定がすごくわかりにくいですね、numpy arrayでappendしていってもよかったのですが、空のarrayが作れないのと、appendはリストの方が早いという話を聞いたことがあって、確認はしていないのですがこの方式にしました。ここは正直もっともいい方法があると思います。
方策の改善
# epsilon-greedyに従いpiを更新
a_prime = np.argmax(Q, axis=0)
for i0 in range(N):
for i1 in range(N):
for i2 in range(N):
for i3 in range(N):
for a in range(num_action):
if a == a_prime[i0,i1,i2,i3]:
pi[a,i0,i1,i2,i3] = 1 - EPSILON + EPSILON/num_action
else:
pi[a,i0,i1,i2,i3] = EPSILON/num_action
更新した価値関数Qに対する最適な行動a_primeを求めます。アルゴリズムの定義にしたがい、それぞれの行動に対する確率を更新します。
結果
2000エピソード生成し、学習した結果を示します。$\epsilon$の初期値を0.3とし、2000エピソードの終わりに0となるように直線的に現象させました。
エピソードの進行に対する収益(return)の結果を下に示します。
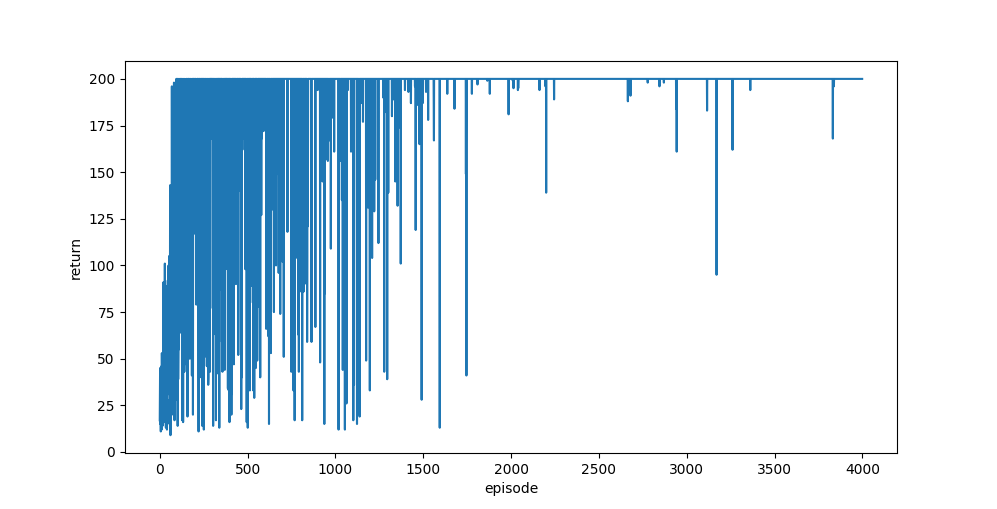
2000エピソードまでが$\epsilon >0$の期間で、ある確率でランダムに行動が選ばれます。この期間は探索を行っているので、収益が安定しませんが、100エピソード以内に最高得点を出す方策を獲得しています。2000エピソード以降は、方策に対してグリーディー(ランダム探索を行わない)に行動しています。ほとんどの区間で最高得点である200を出しています。
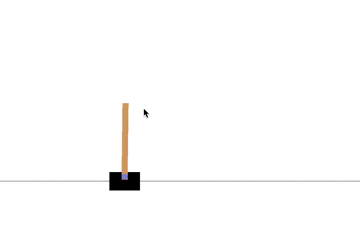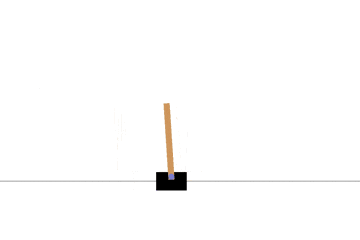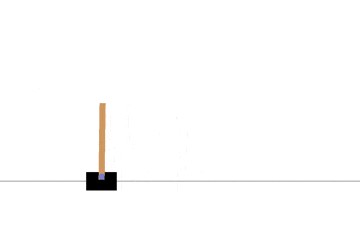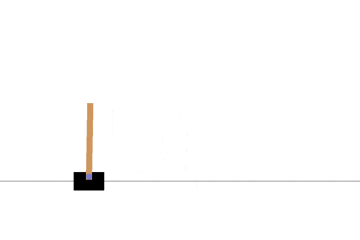
ポールを立てることに成功していますね。もう少し中央で持ちこたえて欲しいですが、そのためには状態空間を離散化する時の範囲をちゃんと設定する必要がありそうです。
おわりに
$\epsilon$-グリーディ手法を用いたモンテカル法でCartpole問題を解きました。モンテカルロ法はこれ以上追求せず、エッセンスを理解するくらいに止めておきます。
ここまで全8回で
- 動的計画法(DP法)
- モンテカルロ法(MC法)
の特徴を見てきました。
DP法は、エピソードを終端まで辿らなくてもブートストラップ(推定中の値を用いて推定値を求める)を用いることができるのが利点ですが、環境のダイナミクスを知っている必要があり、実問題にはほとんど適用できません。
対してMC法では、サンプリングにより環境のダイナミクスを知らなくても価値関数を推定できるところが最大の魅力です。しかし、ブートストラップが使えないため、価値関数を更新するには報酬が確定する終端状態になるまで待たなければなりません。
次回からは、この二つの手法を組み合わせ、お互いの利点をいいとこ取りした手法を扱います。つまりサンプリングにより環境のダイナミクスを知らなくても解け、なおかつブートストラップですぐに価値関数をすぐに更新できる手法を扱っていきます。いわゆる強化学習にやっと入っていきます。