はじめに
数値計算とは何か。英語では numerical computation といい、コンピュータ・プログラミングを駆使して計算を行うものだというのが分かる。
大昔で数値計算はFORTRANでするものだと考えられており、今ではAI開発でPythonでも目立つようになった。大概にライブラリを用いて計算するのが一般的で、Pythonには豊富に存在する。このような知識を持つことに意味はない気もする。では、何に役立つのか。
- OSチューニングができる
プログラミング技術で最低限必要なものは何か、と言われれば「数学」だろう。この手の知識はOSチューニングに生かすことができる。ここで示すサンプル・プログラムは、いささか高度であるというなら本当に初心者向けなのかと言われそうだが、専門数学になるともっと高度である。
- ケーススタディに役立てることができる
四則演算なら簡単にできようものだが、いざや指数関数・対数・三角関数などを書いてみろと言われると、今度はケーススタディが必要になってくる。ケーススタディとは事例研究という実際に使われることを想定した研究のことで、問題解決にそのまま使えるためビジネスでも幅広く利用されている。
例えば現場でsinとcosを同時に計算するプログラムが欲しいと言われたら、Railsあたりでこんな計算をサクッと書けたらそれは凄いだろとなる。(プログラムはRubyコード)
require 'bigdecimal/math'
def sincos(x, prec)
raise ArgumentError, "Zero or negative precision for sin" if prec <= 0
return [BigDecimal::NAN, BigDecimal::NAN] if !x.finite?
n = prec + BigDecimal.double_fig
zero = BigDecimal("0")
one = BigDecimal("1")
twopi = 2 * BigMath.PI(prec + x.exponent)
if x > 30
x %= twopi
else
x -= twopi while x > twopi
end
i = zero
f = one
w = one
a = one
y = zero
sin = zero
cos = zero
while a.nonzero? && ((m = n - (y.exponent - a.exponent).abs) > 0)
m = BigDecimal.double_fig if m < BigDecimal.double_fig
a = w.div(f, m)
case i % 4
when 0
cos = y = cos + a
when 1
sin = y = sin + a
when 2
cos = y = cos - a
when 3
sin = y = sin - a
end
w *= x
f *= (i = i + one)
end
[sin, cos].map{|x| x.round(prec)}
end
プログラムをirbで走らせてみる。$x=1$、任意精度を$20$とする。プログラムでは[sin, cos]の配列が返ってくる。
sincos(BigDecimal(1), 20)
=> [0.84147098480789650665e0, 0.5403023058681397174e0]
級数展開を数値計算する知識があれば、このくらいのプログラミングは実際に数分で書けてしまう。つまり、初級〜中級向けの技術でも十分現場に役立つものである。
イテレーションと収束条件
数式で級数展開は以下のように表示する。
$$[]=\displaystyle\sum_{[]}^{[]}[]$$
$\sum$の下の値は(オブジェクト指向で言えば)イテレータ変数、上の値はその上限である。反復処理ごとに1増しするものと定義される。$\infty$の場合、際限がないことを意味する。
右は反復処理で計算する式である。
自然対数の底だとこのように表示する。
$$e = \displaystyle\sum_{n=0}^\infty\frac{1}{n!}$$
数値計算では反復処理のことをイテレーション iteration、その組み込みルーチンのことをイテレータ iterator、 略記ではiterが使われる。
数値計算プログラムでは反復処理は常套手段であり、微分・積分の双方でこのルーチンはよく使われる。しかし、永遠にループしていては値を得られない。ここでは収束判定を必要とし、筆者はこれを収束条件と呼んでいる。
ここで収束条件とは、真値を得るのを満たす条件のことで、それ以上のイテレーションを必要としないことをいう。
例えばRuby/Railsでの級数展開プログラムでは、公式でのwhile文は
while d.nonzero? && ((m = n - (y.exponent - d.exponent).abs) > 0)
m = BigDecimal.double_fig if m < BigDecimal.double_fig
# :
# :
end
収束の正確性を保持する工夫をこらえ、このようなルーチンとなっている。ここで変数$y$は総和、変数$d$は部分和での差、変数$n$は任意精度、変数$m$は部分和における任意精度である。
この公式の収束条件は、部分和と総和の指数値を任意精度から引いた値が負の値になることである。(製作したのは筆者ではない)
冒頭で示したサンプルプログラムでは、イテレーション内で差分を
a = w.div(f, m)
として求めている。これはa = w/fをメソッドを用いて計算している。任意精度分の差のみを計算するプログラミング・テクニックであり、正確な解を保ったまま速度も向上する。
これはどのようにしてイテレーション内で動作しているのか。
ケーススタディとして自然対数の底を得ることを考えよう。イテレーションの間、部分和と差がどのような様子であるかを見てみる。型はIEEE754の倍精度で、左の値が部分和、右の値が差である。この場合の収束条件は部分和の差が0になることとする。
e = 0; a = 1.0; n = 1.0
begin
puts "%-17.15f %-17.15f | y <- (1/%g!)" % [e, a, n-1]
prev = e; e += a; a /= n; n += 1
end while (e != prev)
#=> 0.000000000000000 1.000000000000000 | y <- (1/0!)
#=> 1.000000000000000 1.000000000000000 | y <- (1/1!)
#=> 2.000000000000000 0.500000000000000 | y <- (1/2!)
#=> 2.500000000000000 0.166666666666667 | y <- (1/3!)
#=> 2.666666666666667 0.041666666666667 | y <- (1/4!)
#=> 2.708333333333333 0.008333333333333 | y <- (1/5!)
#=> 2.716666666666666 0.001388888888889 | y <- (1/6!)
#=> 2.718055555555555 0.000198412698413 | y <- (1/7!)
#=> 2.718253968253968 0.000024801587302 | y <- (1/8!)
#=> 2.718278769841270 0.000002755731922 | y <- (1/9!)
#=> 2.718281525573192 0.000000275573192 | y <- (1/10!)
#=> 2.718281801146385 0.000000025052108 | y <- (1/11!)
#=> 2.718281826198493 0.000000002087676 | y <- (1/12!)
#=> 2.718281828286169 0.000000000160590 | y <- (1/13!)
#=> 2.718281828446759 0.000000000011471 | y <- (1/14!)
#=> 2.718281828458230 0.000000000000765 | y <- (1/15!)
#=> 2.718281828458995 0.000000000000048 | y <- (1/16!)
#=> 2.718281828459043 0.000000000000003 | y <- (1/17!)
#=> 2.718281828459046 0.000000000000000 | y <- (1/18!)
e
#=> 2.7182818284590455
右側が冒頭プログラムa = w.div(f, m)にあたる。このプログラムで精度は16である。
浮動小数点型には機械エプシロン$\epsilon$が定められており、IEEE754倍精度ではだいたい2e-16である。正確に10進に戻せる桁は規格化され、倍精度では16桁が保証されている。
定義と収束半径
数学では関数にすることを考える。ケーススタディで示したものは関数では$f(z)$とする。この関数はテイラー級数と呼ばれ、$z=z_0$とその近傍で解析的な関数を級数に表す。
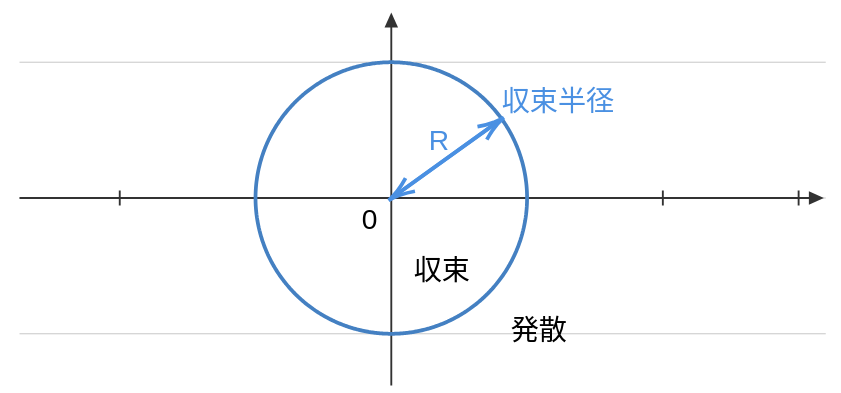
この級数を展開することをテイラー展開(べき級数展開)という。この計算には微分方程式の総和を求めるのに収束半径が関係している。
計算が収束半径$R$の中に収まっているならばこれを収束といい、そうでないならこれを発散という。
この定義は古くから数学者たちの試行錯誤の中で研究され、今の学問体系として落ち着いた。その研究では極限$\displaystyle\lim_{n\to\infty}$がネックとなった。これは意外と0の計算を研究することから建設的に構築されてきた。そのため収束半径は極限で表示されるのが大概である。
収束と発散についてはダランベールの判定法が表示に用いられるのが一般的である。例えば$z_n\neq0$を満たす級数$\sum_{n=1}^\infty z_n$について$\displaystyle\lim_{n\to\infty}|\frac{z_{n+1}}{z_0}|=L$となるとき、
$L<1 \Rightarrow$ 絶対収束する
$L=1 \Rightarrow$ (判定不可能)
$L>1 \Rightarrow$ 発散する
となる。ここで絶対収束とは判定に用いる式が絶対値である場合の収束である。
収束半径はコーシー・アダマールの公式で求められる。これはダランベールの判定法の逆数であり、
$$R=\frac{1}{L}=\lim|\frac{a_n}{a_{n+1}}|$$
で与えられる。
この公式で$R=1/0$となるものは$R=\infty$である。
さて、テイラー級数の解析関数$f(z)$の点$z=z_0$周りでは、次式が与えられる。
$$\begin{array}{rcl}
f(z) & = & \displaystyle\sum_{n=0}^\infty\frac{1}{n!}f^{n}(z_0)(z-z_0)^n \newline
& = & \displaystyle{}f(z_0)+f^\prime(z_0)(z-z_0)+\frac{1}{2!}f^{\prime\prime}(z_0)(z-z_0)^2+\frac{1}{3!}f^{\prime\prime\prime}(z_0)(z-z_0)^3+\cdots
\end{array}$$
原点を$z_0=0$以外とする展開は、大概この方法で計算する。例えば、ケーススタディで示した、べき級数に近似する指数関数・三角関数は、収束半径が$R=\infty$であり、微分方程式をそのまま代用する。
$$\begin{array}{rcl}
e^z & = & \displaystyle\sum_{n=0}^\infty\frac{1}{n!}z^n & = & 1+\frac{1}{1!}z+\frac{1}{2!}z^2+\frac{1}{3!}z^3+\cdots \newline
\cos z & = & \displaystyle\sum_{n=0}^\infty\frac{(-1)^n}{(2n)!}z^{2n} & = & 1-\frac{1}{2!}z^2+\frac{1}{4!}z^4-\frac{1}{6!}z^6+\cdots \newline
\sin z & = & \displaystyle\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)!}z^{2n+1} & = & z-\frac{1}{3!}z^3+\frac{1}{5!}z^5-\frac{1}{7!}z^7+\cdots
\end{array}$$
sinとcosは交代級数と呼ばれ、正負が項ごとに交代する。これは全て正符号にすると双曲線関数$\sinh$と$\cosh$が求まる。
$$\begin{array}{rcl}
\cosh z & = & \displaystyle\sum_{n=0}^\infty\frac{1}{(2n)!}z^{2n} & = & 1+\frac{1}{2!}z^2+\frac{1}{4!}z^4+\frac{1}{6!}z^6+\cdots \newline
\sinh z & = & \displaystyle\sum_{n=0}^\infty\frac{1}{(2n+1)!}z^{2n+1} & = & z+\frac{1}{3!}z^3+\frac{1}{5!}z^5+\frac{1}{7!}z^7+\cdots
\end{array}$$
なおこの定理は$x=0$も含むかどうかでマクローリン展開ともいうが、多くの場合テイラー展開と呼称することが多い。
テイラー展開の収束半径が$R=1$であるような解析的である場合、以下のような展開式がある。
$$\begin{array}{rcl}
\displaystyle\frac{1}{1-z} & = & 1+z+z^2+z^3+\cdots \newline
\ln(1+z) & = & \displaystyle\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n}z^n=z-\frac{1}{2}z^2+\frac{1}{3}z^3-\frac{1}{4}z^4+\cdots
\end{array}$$
実装とその現状
級数展開プログラムを書けるようになったため、ではどのような現場で必要になるか。
冒頭で示したサンプルプログラムは解析的なsinとcosを同時に求めるということをしていて、実に大胆な振る舞いを見せている。
しかしながら、解析的な数値計算で解を導出することは、実装例としても意外と少ない。
例えばGNU Cに昔からあるsincos()は以下のようなシンプルな実装である。
void
sincos(double x, double *vsin, double *vcos)
{
*vsin = sin(x); *vcos = cos(x);
}
sin()、 cos()、 atan()などは大概CPU命令にあるので、それを組み込みにすれば自前で実装する必要がない。開発ではそのような事情も多いのが伺える。
では、実際の実装はどうかというと、大概に組み込みで使うツールを用いて計算するがほとんどであり、応用分野における基礎知識にすぎていない。ここで言及していることは組み込み開発に培われるのが専らと言える。