ニューラルネットワークの計算の仕組み（ニューロン数とバイアスの役割）

1. 概要

入力層、中間層、出力層の3層のニューラルネットワークを作成するときに、中間層のニューロン数とバイアスの有無がニューラルネットワークによる計算に与える影響について記述します。バイアスという言葉は、機械学習の分野ではデータの偏りや予測モデルと真のモデルとの差のことを表したりしますが、ここではニューラルネットワークの常に1を出力するニューロンのことを指すとします。

この記事は、ニューラルネットワークの順方向の計算過程の仕組みについてのみ記述いたします。ニューラルネットワークの重みを、予測した値と教師データとの誤差から再計算するいわゆるバックプロパゲーション(誤差逆伝搬)については取り扱いません。

結論です。

• ニューロン数が増えると複雑な関数を近似することができる。
• バイアスが無いと、入力が 0 の地点が固定された関数しか近似することができない。

近似とは、いくつかの関数のグラフを足し合わせて、望む形をしたグラフを作り出すようなものです。入力が 0 の地点は、例えば活性化関数が tanh の場合、(0,0)の原点になります。

2. ニューラルネットワークによる計算とは？

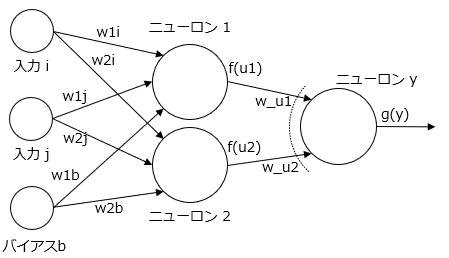
3層のニューラルネットワークです。3層とは列が3つあるということで、左から入力層、ニューロン1,2があるところを中間層、ニューロンyを出力層と呼びます。小さい丸は入力またはバイアス、大きな丸はニューロン、どちらも数値が1つ割り当てられます。矢印はエッジとよび、重みと呼ばれる1つの数値が割り当てられます。

ニューラルネットワークによる計算とは、入力i、入力jに値をセットして、エッジを介してニューロン1,2の値、そしてそこからニューロンyの値を計算してニューロンyからの出力値を計算することです。

ニューラルネットワークは重みの数値を適切に変えて、望む出力を計算できるようにします。この重みの数値をデータから自動的に計算することを学習と呼びます。ただし学習の仕組みについては本記事では扱いません。

ニューロンを1つ取り出して説明していきます。1つのニューロンからの出力値は、次のように計算されます。

y = f(u) \\
u = x_1 \times w_1 + x_2 \times w_2 + ...

出力yはニューロンの値uを活性化関数fを通して得られた値で、uは入力xに重みwがかけられたものです。ニューロンに複数の入力がある場合、それらは足し合わされてuの値になります。

具体的には、例えば入力の値が -1 から 2 の間の数値であり重みが 1 と仮定すると、出力は以下の図の緑の枠のようになります。

活性化関数はtanhという上記の青の線の形をしたものとしています。重みは、この活性化関数からどこを切り取るかを指定するようなものです。例えば重みを 1 から 2 に変更すると、緑の枠がピンクの枠に拡大されるという感じです。

2.1. 2ニューロン、バイアスありの計算例

ここからはより具体的にニューラルネットワークの計算を説明していきます。

まず学習したいデータを次のように定義します。

学習したデータは4点のデータでできています。学習したいデータとは、この4点のデータのx軸の値をニューラルネットワークの入力にセットすると、出力にy軸の値が返るようにしたいというデータです。例えば入力を-1とするとニューラルネットワークは-3を出力する、入力が1なら1が出力されるという感じです。

次に機械学習モデルのネットワーク構造を作成します。ここでは3層で入力1つ、中間層のニューロンは2つ、出力層は1つです。左下にあるのはバイアスと呼ばれ、このバイアスは常に1がセットされる入力と同じです。

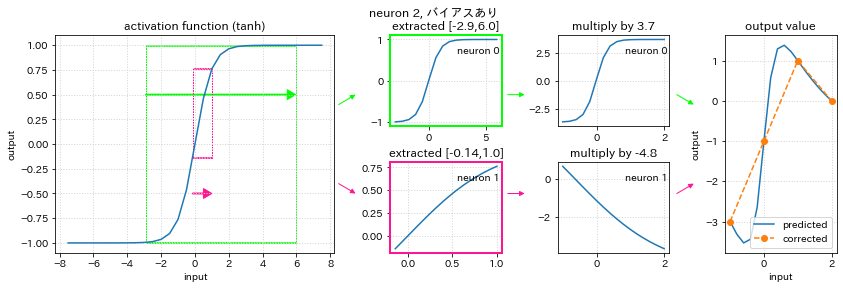
この例は、すでに学習が終了したニューラルネットワークの重みでどのように入力値から出力値を計算しているのかを示しています。

1列目は活性化関数が表示されています。学習したいデータは -1 から 2 の間の数値なので、ニューロン1の重み、ニューロン2の重みでそれぞれ拡大縮小された抽出枠がニューラルネットワークの学習で求められます。図の左側の緑とピンクの枠です。抽出した部分を拡大すると図の2列目のようになります。

次に出力層の重みによって抽出枠がさらに拡大縮小反転したものが3列目です。

そして変換後の2つのグラフを足し合わせると4列目の出力のグラフとなります。

グラフを足し合わせる、の追加説明

グラフを足し合わせるとは、2つのグラフのx軸を揃えてy軸の値を足すことです。例えば上上図の上の青とオレンジの2つのグラフを足し合わせると、下の緑のグラフとなります。

4列目の右の図には、参考に学習したいデータをオレンジの点線で描画しています。4つの点はいずれもニューラルネットワークが計算する青い線と一致しています。よって学習には成功しているといえます。

学習したいデータの4つの点の間は、直線で描画しているオレンジと、グラフを足し合わせて描画しているニューラルネットワークの出力と一致していませんが、これは学習したいデータでは定義されていない部分なので学習が成功したかどうかの評価では対象外となります。

2.2. 2ニューロン、バイアスなしの計算例

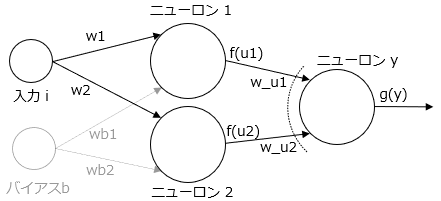
つぎに中間層に入るバイアスを機械学習モデルから削除してみます。上図の薄くなったバイアスは今回は除外されています。

4列目の出力を見ると、学習したいデータのオレンジの4点と、ニューラルネットワークの出力である青い線の同じx軸のy軸の位置はずれています。よって学習は成功しているとはいえません。この理由はバイアスがないためであり、バイアスは活性化関数からの抽出枠を決めるときに次のような役割をもっているといえます。

バイアスあり	バイアスなし
抽出枠を横にも移動できる	抽出枠は原点がピン止めされた拡大縮小しかできない

バイアスがない場合、すべての入力が 0 のときに重みの数値がいくつであっても必ず 0 をそのニューロンは出力します。計算式は次のようです。

u = 0 \times w_1 + 0 \times w_2 + .... = 0 \\
y = tanh(0) = 0

これは活性化関数から抽出する枠でいうと、重みを変更して抽出枠を拡大縮小するときに、原点を固定して伸ばしたり縮めたりしていることになります。ここに出力層の重みをかけても 0 に何をかけても 0 なので枠の原点の位置は移動することはありません。

今回の学習したいデータは、入力が 0 のとき出力が -1 になって欲しいデータでした。しかしバイアスがないと2つのニューロンの重みと出力の重みをいくら変更しても常に 0 が出力されるため、学習することは不可能です。

専門的な言葉でいうと、バイアスがないと抽出枠は線形変換で伸び縮みされます。バイアスがあるとアフィン変換といって原点の位置を移動できる変換ができます。

2.3. ニューロン数と学習結果

出力層の値は、その前のニューロンからの入力を足し合わせたものになります。そしてニューロンからの出力はすでに説明した通り、活性化関数の一部を切り取ったものです。

今回の学習したいデータは、グラフでいうと山があります。この山は活性化関数のtanhにはどこを切り出してもないため、今回の学習したいデータの場合はニューロン数が1つでは学習することができません。

ニューロン数1	ニューロン数2
活性化関数の変形はできない	活性化関数を変形できる

ニューロン数1のときには活性化関数の形を保持した出力になり、2つだと形を変えることができます。より複雑なグラフを作りたい場合には、ニューロンの数をさらに増やす必要があります。

3. Google Colaboratoryでニューロン数1,2、バイアスあり/なしを実際に学習してみる。

ここからは、中間層のニューロン数が1と2、それぞれにバイアスあり／なしの計4つのモデルを作成して実際にモデルの学習をしていきます。

まず、実行環境の準備をします。プログラムは、Google Colaboratoryにコピーすると実行することができます。

準備

# 日本語matplotlibのインストール
!pip install japanize-matplotlib
import numpy as np
from numpy.random import seed
import tensorflow as tf
from tensorflow import keras
import matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib
import math

# 各種のバージョンを確認する
!python --version
print(f"numpy {np.__version__}")
print(f"tensorflow {tf.__version__}")
print(f"matplotlib {matplotlib.__version__}")

実行結果例

...(省略)...
Python 3.8.10
numpy 1.21.6
tensorflow 2.9.2
matplotlib 3.2.2

4. 学習しようとしているデータ

4種類のデータを学習して再現することを試みます。

学習データの生成と描画

# 入力データと正解データになる出力値を定義する。
trains = np.array([
    [[-1,-1],[0,0],[1,1],[2,2]],
    [[-1,-2],[0,0],[1,2],[2,1]],
    [[-1,-2],[0,-1],[1,0],[2,1]],
    [[-1,-3],[0,-1],[1,1],[2,0]],
])
train_labels = ["原点通る直線","原点通る折れ線","原点通らない直線","原点通らない折れ線"]

# トレーニングデータを描画する。
fig,ax = plt.subplots(facecolor="white")
for i,data in enumerate(trains):
  ax.plot(data[:,0],data[:,1],label=train_labels[i],marker="o")
ax.grid()
# 原点の位置を矢印で描画する。
ax.arrow(-0.4,0.15,0.09,-0.02,width=0.06)
ax.text(-0.48,0.32,"(0,0)")
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.legend()
plt.show()

実行結果例

図中の矢印は原点を示しています。data 0とdata 1は原点を通っています。

5. 4種類の機械学習モデル

入力、中間、出力層の3層ニューラルネットワークとします。4つのモデルで異なる部分は、中間層のニューロン数とバイアスを使用するかどうかです。

モデルの生成関数とパラメータ一覧

# モデルの生成、中間層のニューロンの数とバイアスを使用するかどうかを指定する。
def build_model(n_neuron,use_bias):
  model = keras.Sequential([
      keras.layers.Input((1)),
      keras.layers.Dense(n_neuron,use_bias=use_bias,activation="tanh"),
      keras.layers.Dense(1,use_bias=False), #出力層のバイアスは、計算をシンプルにするために使用しない。
  ])
  model.compile(optimizer="sgd",loss="mse")
  return model

# モデルのパラメータ一覧（ニューロン数とバイアスの有無）
model_params = [(1,False),(1,True),(2,False),(2,True)]

このプログラムを実行したときの出力は特にありません。

6. モデルの学習

モデルの学習

# 1つのモデルごとに、モデル生成のパラメータ、学習履歴としての損失などを記録する。
histories = []

for model_param in model_params:
  hists = []
  for data_i,data in enumerate(trains):
    # モデルを生成する
    model = build_model(*model_param)
    # 学習する。トレーニングデータ数が少ないのでbatch_sizeは1で実行する。
    h = model.fit(data[:,0],data[:,1],epochs=10000,batch_size=1,verbose=0)
    # モデル生成のパラメータ等を保存する。
    hists.append((model_param,model,data_i,data,h.history["loss"]))
    print(f"params={model_param}, data_i={data_i}, last loss={h.history['loss'][-1]}")
  # このモデルパラメータで学習した履歴を保存する。
  histories.append(hists)

4つのモデル×4つのデータで計16回の学習を行います。このプログラムを実行すると終わるまで10分ぐらいはかかります。

実行結果例

params=(1, False), data_i=0, last loss=0.0024928697384893894
params=(1, False), data_i=1, last loss=0.17066550254821777
params=(1, False), data_i=2, last loss=0.7595527172088623
params=(1, False), data_i=3, last loss=1.4409029483795166
params=(1, True), data_i=0, last loss=0.0029093101620674133
params=(1, True), data_i=1, last loss=0.17063607275485992
params=(1, True), data_i=2, last loss=0.002287365263327956
params=(1, True), data_i=3, last loss=1.1168204545974731
params=(2, False), data_i=0, last loss=0.001335871173068881
params=(2, False), data_i=1, last loss=9.316103444234614e-10
params=(2, False), data_i=2, last loss=0.7599421739578247
params=(2, False), data_i=3, last loss=0.9392339587211609
params=(2, True), data_i=0, last loss=0.00017486978322267532
params=(2, True), data_i=1, last loss=3.4987532870900395e-09
params=(2, True), data_i=2, last loss=3.404624294489622e-05
params=(2, True), data_i=3, last loss=3.099086143265595e-08

7. 学習結果の表示

学習結果の表示

# k桁の有効数字を求める
def sig_digits(x,k=2):
  return round(float(x),k-math.floor(math.log10(abs(x)))-1) if x!=0 else 0

# 記録したhistoriesから各モデル、各データの最終損失を抽出します。
loss = np.array([list(map(lambda h:sig_digits(h[4][-1]),hists)) for hists in histories])
# 損失が 0.01未満とそれ以外でテーブルのセルの色を変えます。
# 色一覧 https://matplotlib.org/stable/gallery/color/named_colors.html
colors = np.where(loss<0.01,"skyblue","lightcoral")

# また記録からモデル生成のパラメータを取得します。
params = [hists[0][0] for hists in histories]

# テーブル形式で表示します。
# 行はモデル生成のパラメータ、列は学習データに対応します。
fig,ax = plt.subplots(facecolor="white")
ax.axis("off")
ax.table(cellText=loss,
         rowLabels=params,
         colLabels=[f"data {i}" for i in range(len(trains))],
         bbox=[0,0,1,1],
         cellColours=colors,
         rowColours=["lightgray"]*loss.shape[0],
         colColours=["lightgray"]*loss.shape[0],
         )
plt.show()

実行結果例

学習できたところは青、できないところは赤で示されています。バイアスがないと、原点を通らないデータは学習することができません。またニューロンが1つだと折れ線は学習できません。

学習できた／できない判定の詳細

学習するデータは折れ線の場合にはy軸の幅が 2 , 直線では 3 あります。その小さい方の 5% の誤差を許容すると仮定すると 損失関数である mse(平均二乗誤差)は、(2 * 0.05)^2 = 0.01となります。そこで、今回は 0.01 よりも平均二乗誤差が小さい場合には学習できた、としています。

7.1 4種類のモデルの学習過程の詳細

ここでは学習したいデータは、原点を通らない折れ線のものとします。

7.2. ニューロン数1、バイアスなし

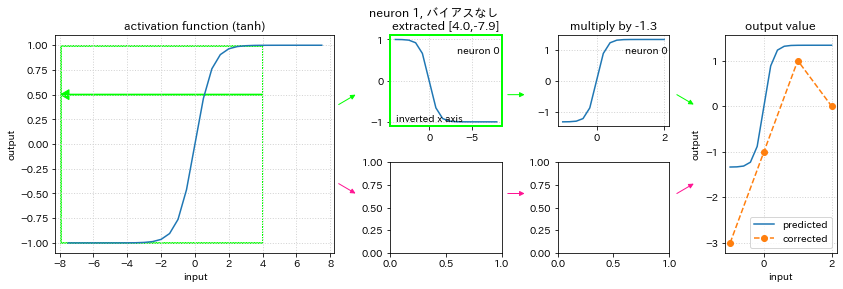
まず上図の空白部分は、ニューロンが2つではないため下の部分が表示されないことを表しています。

結果は、学習したいデータのグラフに最も似ているところを活性化関数のグラフから抜き出しています。正解データの折れ線部分は、活性化関数には無いため学習することができていません。

7.3. ニューロン数1、バイアスあり

バイアスなしに比べて活性化関数の原点から横にずらして抽出枠を取っても良いため、選んだ抽出枠は異なっています。ただ正解データの折れ線部分はバイアスなしと同様に学習できていません。

7.4. ニューロン数2、バイアスなし

学習したい折れ線を作り出すために、ニューラルネットワークの出力は上下に変化するグラフになっています。ただバイアスがないのでグラフは必ず原点を通る必要があります。このため、学習したいデータとは少しずれているグラフとなっています。

7.5. ニューロン数2、バイアスあり

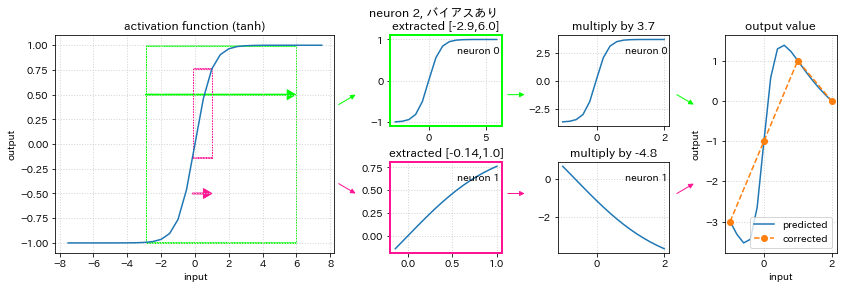
バイアスありにすると活性化関数からの抽出枠が原点にピン止めされないので、正解データの入力 0 のときの出力 -1 も学習できるようになっています。

8. まとめと補足

よりよく学習するためには、計算時間やメモリなどのリソースを気にしなければ、ニューロンの数を増やしバイアスありにする方が良いです。ただしその場合は、過学習の恐れがあります。

機械学習は、学習に使用するデータをトレーニングデータと呼び、学習後に学習ができたかどうかを評価するのは評価データと呼びトレーニングデータとは予め分けておきます。その理由は、世の中のすべてのデータを取得することができるわけではないので、未知のデータにも対応できるようにするためです。この未知のデータが学習時に使用しなかった評価データということです。過学習とは、トレーニングデータにはうまく適用できるけど評価データには上手くいかない、という状態です。

よって理想的には、トレーニングデータからその特徴を機械学習モデルが学習し、その特徴は同じデータ元から発生する評価データでも持っている、となることです。そもそも特徴とは全体から部分的に抽出されるものなので、この部分的というところがニューロン数やバイアス、そして今回は触れませんでしたがニューラルネットワークの層の数で過不足なくあらわされていると良いニューラルネットワークの構造であると言えると思います。