趣味でスペクトル法_#003_2次元周期流

概要

　文献¹²を参考に，2次元非圧縮性流体の数値解析プログラムをFortranで作成した．2次元周期流を仮定し，渦度輸送方程式をスペクトル法で解いた．離散フーリエ変換にはIntel MKL³を用いた．

$1024^2$自由度の解析．Paraview⁴で可視化した．

記事内へのリンク

支配方程式の導出
初期条件の与え方
2次元DFT
非線形項の評価（変換法）
時間積分法
計算例
ソースコード

更新履歴

2019.12.01 : 公開

支配方程式の導出

　2次元の非圧縮性流体を仮定し，スペクトル法で解く支配方程式を導出する．¹⁵⁶

渦度輸送方程式の導出

　基礎方程式は次に示す連続の式（質量保存則）とNavier-Stokes方程式（運動量保存則）である．⁵⁶

連続の式

\begin{align}
\nabla\cdot\mathbf{u}
=
\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}
=
0
\tag{1}
\end{align}

Navier-Stokes方程式

$$
\begin{align}
\frac{\partial \mathbf{u}}{\partial t}+\mathbf{u}\cdot\nabla\mathbf{u}
=-\nabla p +\nu\nabla^2\mathbf{u}
\tag{2}\
\end{align}
$$

諸量は代表長さ・速さで無次元化している．ここで，$p=\rm{静圧/密度}$，$\nu=1/\rm{Re}=const.$である．$x$方向速度$u$, $y$方向速度$v$についてそれぞれ書き下せば，次のようになる．
$$
\begin{align}
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}
=-\frac{\partial p}{\partial x}
+\nu\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right)
\tag{3}
\end{align}
$$

$$
\begin{align}
\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}
=-\frac{\partial p}{\partial y}
+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right)
\tag{4}
\end{align}
$$

渦度輸送方程式

渦度$\zeta$を導入し，式(2)を扱いやすい形に変形する．ここで$\zeta$の定義は，
$$
\begin{align}
\zeta=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}
\end{align}
$$
であり，3次元で定義される渦度$\omega=\nabla\times\mathbf{u}$の第3成分と一致する．

　式(4)を$x$で偏微分した式から，式(3)を$y$で偏微分した式を引くと，

\begin{align}
L.H.S.
&=
\frac{\partial}{\partial x}\left(
\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}
\right)
-
\frac{\partial}{\partial y}\left(
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}
\right)\\
&=
\frac{\partial \zeta}{\partial t}
+u\frac{\partial \zeta}{\partial x}+v\frac{\partial \zeta}{\partial y}\\
R.H.S.
&=
\frac{\partial}{\partial x}\left(-\frac{\partial p}{\partial y}
+\nu\nabla^2v
\right)
-
\frac{\partial}{\partial y}\left(-\frac{\partial p}{\partial x}
+\nu\nabla^2u
\right)\\
&=\nu\nabla^2\zeta
\end{align}

よって，渦度$\zeta$に対する方程式（渦度輸送方程式）が得られる．

$$
\begin{align}
\frac{D \zeta}{D t}=\frac{\partial \zeta}{\partial t}
+u\frac{\partial \zeta}{\partial x}+v\frac{\partial \zeta}{\partial y}
=\nu\nabla^2\zeta
\tag{5}
\end{align}
$$
ここで2次元のラプラシアンと実質微分は次のように定義される．
$$
\begin{align}
\nabla^2=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial x^2}
,;;
\frac{D}{Dt}=\frac{\partial }{\partial t}
+u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}.
\end{align}
$$

流れ関数の導入

　式(5)に流れ関数$\psi$を導入する．$\psi$を文献¹に従い，次のように定義する．
$$
\begin{align}
u=-\frac{\partial \psi}{\partial y},;;v=\frac{\partial \psi}{\partial x}.
\end{align}
$$
一般的な定義⁵と符号が逆であるが，このように定義することで渦度$\zeta$との関係式が次のようになる．
$$
\begin{align}
\zeta=\nabla^2\psi
\tag{6}
\end{align}
$$
よって，渦度輸送方程式（式(5)）は$\psi$のみに関する偏微分方程式となる．
$$
\begin{align}
\frac{D (\nabla^2\psi)}{D t}
=\nu\nabla^2(\nabla^2\psi)
\tag{7}
\end{align}
$$

フーリエ空間での支配方程式

境界条件

　計算領域を$0\leq x,y \leq 2\pi$として，周期境界条件をもちいる．すなわち任意の時間$t$における境界の$\psi$の値は，
$$
\begin{align}
\psi(0,y,t)=\psi(2\pi,y,t),;;\psi(x,0,t)=\psi(x,2\pi,t)\
\end{align}
$$
を満たす．

関数展開

　$x,y$の両方向に周期的なので，展開関数としてフーリエ級数を選択する．$\psi(x,y,t)$は次のように定義される．
$$
\begin{align}
\psi(x,y,t)=\sum_{k=-N/2}^{N/2-1}\sum_{l=-N/2}^{N/2-1}
a_{kl}(t)e^{ikx}e^{ily}
\tag{8}
\end{align}
$$
展開係数$a_{kl}(t)$の自由度は$\psi$が実数であることから，

$$
\begin{align}
a_{(-k)(-l)}=a^*_{kl}
\end{align}
$$

の制約がかかり，$N^2$となる．ここで，$^*$は複素共役を意味する．

\begin{align}
\because \;\;{\rm Im}\left[a_{kl}e^{i(kx+ly)}-a_{(-k)(-l)}e^{-i(kx+ly)}\right]=0
\end{align}

常微分方程式の導出

　展開係数$a_{kl}$に対する常微分方程式を導く．式(7)の残差の式
$$
R(x,y,t)=\frac{D (\nabla^2\psi)}{D t}
-\nu\nabla^2(\nabla^2\psi)
$$
に$\psi$の展開式（式(8)）を代入し，$e^{-ikx}e^{-ily}$をかけて，計算領域全域で積分したものが$0$になるようにすれば良い．すなわち，次式を要請する．
$$
\int_{0}^{2\pi}\int_{0}^{2\pi}R(x,y,t)e^{-ikx}e^{-ily}dxdy=0
$$

時間微分項

\begin{align}
&\int_{0}^{2\pi}\int_{0}^{2\pi}\frac{\partial(\nabla^2\psi)}{\partial t}
e^{-ikx}e^{-ily}dxdy\\
&=
\int_{0}^{2\pi}\int_{0}^{2\pi}\frac{\partial}{\partial t}\left[\nabla^2\left(\sum_{k=-N/2}^{N/2-1}\sum_{l=-N/2}^{N/2-1}
a_{kl}(t)e^{ikx}e^{ily}\right)\right]e^{-ikx}e^{-ily}dxdy\\
&=
\sum_k\sum_l\left\{-(k^2+l^2)\frac{d a_{kl}}{d t}\right\}
\int_{0}^{2\pi}\int_{0}^{2\pi}dxdy\\
&=
-(2\pi)^2\sum_k\sum_l(k^2+l^2)\frac{d a_{kl}}{d t}
\end{align}

線形項

\begin{align}
&\int_{0}^{2\pi}\int_{0}^{2\pi}\nu\nabla^2(\nabla^2\psi)
e^{-ikx}e^{-ily}dxdy\\
&=-(2\pi)^2\sum_k\sum_l(k^2+l^2)^2a_{kl}
\end{align}

非線形項

　変換法で評価するので，$\psi$に展開式を代入して変形したりはしない．また，上述の2項で付随した$(2\pi)^2$で割ると，
$$
\begin{align}
F_{kl}=\frac{1}{(2\pi)^2}\int_0^{2\pi}\int_0^{2\pi}
\left(
u\frac{\partial \zeta}{\partial x}+v\frac{\partial \zeta}{\partial y}
\right)e^{-ikx}e^{-ily}dxdy
\tag{9}
\end{align}
$$
となり，$F_{kl}$は非線形項の展開係数とみなせる．（かつ2次元のFFTが適用できそうな式形になる）

常微分方程式

以上を踏まえて，流れ関数$\psi$の展開係数$a_{kl}$に対する常微分方程式は，次のようになる．
$$
\begin{align}
\frac{d a_{kl}}{d t}=\frac{F_{kl}}{(k^2+l^2)}-\nu(k^2+l^2)a_{kl}
\tag{10}
\end{align}
$$

物理空間における格子点

　物理空間の自由度も同様に$N^2$として，$0\leq x,y \leq 2\pi$の計算領域に格子点$(x_m,y_n)$を置く．
$$
\begin{align}
x_m=\frac{2\pi}{N}m;,;;;y_n=\frac{2\pi}{N}n;;(0\leq m,n\leq N-1)
\tag{11}
\end{align}
$$

初期条件

　式(10)は流れ関数$\psi$の展開係数$a_{kl}$に関する常微分方程式である．しかし，流れ場は$\psi$よりも渦度$\zeta$で定義する方がわかりやすい（と思う）．よって，$\zeta(x,y,0)$で与えて，$\psi(x,y,0)$に変換する．$\zeta$の展開係数を$b_{kl}$と置くと，式(8)と同様に
$$
\begin{align}
\zeta(x,y,0)=\sum_{k=-N/2}^{N/2-1}\sum_{l=-N/2}^{N/2-1}
b_{kl}(0)e^{ikx}e^{ily}
\tag{12}
\end{align}
$$
と展開できる．後に述べる2次元FFTで$\zeta\rightarrow b_{kl}$の変換ができる．
$$
\begin{align}
b_{kl}=\frac{1}{2\pi}\int_0^{2\pi}\int_0^{2\pi}\zeta e^{-ikx}e^{-ily}dxdy
\tag{13}
\end{align}
$$

流れ関数への変換

　式(6)で示された$\zeta$と$\psi$の関係は，2次元のPoisson方程式である．
$$
\begin{align}
\zeta(x,y,0)=\nabla^2\psi(x,y,0)=\frac{\partial^2 \psi}{\partial x^2}+\frac{\partial^2 \psi}{\partial y^2}
\tag{14}
\end{align}
$$
スペクトル法では，Poisson方程式は反復法を用いずに解くことができる．上式から残差を定義し，重み$e^{-ikx}e^{-ily}$をかけて計算領域で積分する．式(8),(11),(12)を用いれば，
$$
\begin{align}
a_{kl}=-\frac{b_{kl}}{k^2+l^2}
\tag{15}
\end{align}
$$
が得られる．よって$b_{kl}$から$a_{kl}$を求められる．

2次元DFT

定義

　まず，順方向・逆方向のDFTを定義する．格子点$(x_m,y_n)$を定義して，

$$
\begin{align}
x_m=\frac{2\pi}{M}m;;(0\leq m\leq M-1),;;;
y_n=\frac{2\pi}{N}n;;(0\leq n\leq N-1)
\end{align}
$$
関数$g(x,y)$をその格子点上で定義する．
$$
g_{mn}=g(x_m,y_n)
$$

正変換

\begin{align}
G_{kl}
=\frac{1}{MN}
\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}
g_{mn}
\exp\left(-2\pi i \frac{m\cdot k}{M}\right)
\exp\left(-2\pi i \frac{n\cdot l}{N}\right)\tag{16}\\
(0\leq k\leq M-1,\;\; 0\leq l\leq N-1)
\end{align}

逆変換

\begin{align}
g_{mn}=\sum_{k=0}^{M-1}\sum_{l=0}^{N-1}G_{kl}
\exp\left(2\pi i \frac{m\cdot k}{M}\right)
\exp\left(2\pi i \frac{n\cdot l}{N}\right)\tag{17}\\
(0\leq m\leq M-1,\;\; 0\leq n\leq N-1)
\end{align}

実DFT

　$g$を実数とする，2次元実DFTは，1次元複素DFTと1次元実DFTを組み合わせとみなせる（多次元FFTのアルゴリズムは必ずそうとは限らないが）．例えば逆変換（式(17)）は，

• 複素IDFT．中間変数$g'_{kn}$は複素数．$(0\leq k\leq M-1,;; 0\leq n\leq N-1)$

\begin{align}
g'_{kn}&=\sum_{l=0}^{N-1}G_{kl}
\exp\left(2\pi i \frac{n\cdot l}{N}\right)\\
\end{align}

• 実IDFT．$g_{mn}$は実数．$(0\leq m\leq M-1)$

$$
\begin{align}
g_{mn}&=\sum_{k=0}^{N-1}g'_{kn}
\exp\left(2\pi i \frac{m\cdot k}{M}\right)\
\end{align}
$$

級数展開式の変形

　例えば，式(8)で示された$a_{kl}\rightarrow \psi$の変換に式(17)の逆変換を適用することを考える．

（再掲）
$$
\begin{align}
\psi(x,y,t)=\sum_{k=-N/2}^{N/2-1}\sum_{l=-N/2}^{N/2-1}
a_{kl}(t)e^{ikx}e^{ily}
\tag{8}
\end{align}
$$
$x,y$も式(11)のように離散化する．
$$
\begin{align}
\psi(x_m,y_n)=\psi_{mn}=\sum_{k=-N/2}^{N/2-1}\sum_{l=-N/2}^{N/2-1}
a_{kl}(t)
\exp\left(2\pi i \frac{m\cdot k}{N}\right)
\exp\left(2\pi i \frac{n\cdot l}{N}\right)\tag{18}
\
(m,n=0,..,N-1)
\end{align}
$$
問題になるのは，$k,l$のとる範囲である．

　まず，内側の$\sum_l$ : $y$方向の級数展開について，

\begin{align}
\sum_{l=-N/2}^{-1}a_{kl}\exp\left(2\pi i \frac{l\cdot n}{N}\right)
&=\sum_{l=N/2}^{N-1}a_{k(l-N)}\exp\left(2\pi i \frac{(l-N)\cdot n}{N}\right)\\
&=\sum_{l=N/2}^{N-1}a_{k(l-N)}\exp\left(2\pi i \frac{l\cdot n}{N}\right)\\
\end{align}

より，中間変数$\psi'_{kn}$（複素数）は

\begin{align}
\psi'_{kn}
&=\sum_{l=-N/2}^{N/2-1}a_{kl}\exp\left(2\pi i \frac{l\cdot n}{N}\right)\\
&=\sum_{l=0}^{N/2-1}a_{kl}\exp\left(2\pi i \frac{l\cdot n}{N}\right)
+\sum_{l=N/2}^{N-1}a_{k(l-N)}\exp\left(2\pi i \frac{l\cdot n}{N}\right)\\
&=\sum_{l=0}^{N-1}w_{kl}\exp\left(2\pi i \frac{l\cdot n}{N}\right)
\end{align}

ここで，$w_{kl}$の定義は，

\begin{equation}
w_{kl}=
\begin{cases}
a_{kl}& 0\leq l \leq N/2-1\\
a_{k(l-N)}& N/2 \leq l \leq N-1
\end{cases}
\end{equation}

となる．よって$\sum_l$は長さ$N$の複素IDFTに変形できた．

　次に，$\sum_k$ : $x$方向の級数展開について
$$
\begin{align}
\psi_{mn}
=\sum_{k=-N/2}^{N/2-1}
\psi'_{kn}
\exp\left(2\pi i \frac{k\cdot m}{N}\right)\
\end{align}
$$

である．$\psi_{mn}$は実数なので，$\psi_{(-k)n}'=\psi^{\prime *}_{kn}$の制約が生じる．

\begin{align}
\psi_{mn}
&=\sum_{k=-N/2}^{N/2-1}
\psi'_{kn}
\exp\left(2\pi i \frac{k\cdot m}{N}\right)\\
&=\sum_{k=0}^{N/2-1}
\psi'_{kn}
\exp\left(2\pi i \frac{k\cdot m}{N}\right)
+\sum_{k=1}^{N/2}
\psi'_{(-k)n}
\exp\left(2\pi i \frac{(-k)\cdot m}{N}\right)\\
&=\sum_{k=0}^{N/2-1}
\psi'_{kn}
\exp\left(2\pi i \frac{k\cdot m}{N}\right)
+\sum_{k=1}^{N/2}
\psi'^*_{kn}
\exp\left(-2\pi i \frac{k\cdot m}{N}\right)\\
&=\psi_{0n}
+2\sum_{k=1}^{N/2-1}\left[{\rm Re}(\psi'_{kn})\cos\left(2\pi\frac{k\cdot m}{N}\right)-{\rm Im}(\psi'_{kn})\sin\left(2\pi\frac{k\cdot m}{N}\right) \right]
\end{align}

自由度$N$の（1次元）実IDFTは通常，上式に$k=N/2$の項を加えた次の式を計算するように(FFTで)実装されている¹.
$$
\begin{align}
f(m)
&=F_{0}
+\left(-1\right)^mF_{N/2}
+2\sum_{k=1}^{N/2-1}\left[{\rm Re}(F_{m})\cos\left(2\pi\frac{k\cdot m}{N}\right)
-{\rm Im}(F_{m})\sin\left(2\pi\frac{k\cdot m}{N}\right) \right]
\end{align}
$$
よって上式で$F=\psi',;;F_{N/2}=0$とすれば，$\sum_k$の項は長さ$N$の実IDFTを用いて計算できる．この逆は，$x$方向の実DFT$\rightarrow$$y$方向の複素DFTを行えば良い．

　結局，式(8),(13)のような"フーリエ空間で定義される展開係数"$\leftrightarrow$"物理空間で定義される値"の変換は，2次元DFTを利用して計算できる．

非線形項の評価

　次式で定義される展開係数$F_{kl}$の効率的な評価方法を述べる．

（再掲）
$$
\begin{align}
F_{kl}
&=\frac{1}{(2\pi)^2}\int_0^{2\pi}\int_0^{2\pi}
\left(
u\frac{\partial \zeta}{\partial x}+v\frac{\partial \zeta}{\partial y}
\right)e^{-ikx}e^{-ily}dxdy\
\tag{9}
\end{align}
$$

変換法

　フーリエ空間で計算するよりも，IFFTを使って物理空間上の格子点で値を評価しFFTでフーリエ空間に戻す方が計算量が削減できる．ただし，この時aliasing誤差が生じるため，これを取り除く工夫をしなくてはならない．

計算量の削減

　非線形項を次のように変形することで，FFTの回数を減らすことができる¹．

\begin{align}
u\frac{\partial \zeta}{\partial x}+v\frac{\partial \zeta}{\partial y}
&=\frac{\partial u\zeta}{\partial x}+\frac{\partial v\zeta}{\partial y}\\
&=\frac{\partial }{\partial x}
\left\{
u\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)
\right\}
+\frac{\partial }{\partial y}
\left\{
v\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)
\right\}\\
&=\frac{\partial }{\partial x}
\left(
\frac{\partial uv}{\partial x}
+\frac{1}{2}\frac{\partial v^2}{\partial y}
-\frac{1}{2}\frac{\partial u^2}{\partial y}\right)
+\frac{\partial }{\partial y}
\left(
\frac{1}{2}\frac{\partial v^2}{\partial x}
-\frac{1}{2}\frac{\partial u^2}{\partial x}
-\frac{\partial uv}{\partial y}\right)\\
&=\left(\frac{\partial^2}{\partial x^2}-\frac{\partial^2}{\partial y^2}\right)(uv)
+\frac{\partial^2}{\partial x \partial y}(v^2-u^2)
\end{align}

$uv,v^2-u^2$それぞれに対する展開係数を$A_{kl},B_{kl}$と置けば，

\begin{align}
F_{kl}=-(k^2-l^2)A_{kl}-klB_{kl}\tag{19}
\end{align}

と計算できる．

変形前

$a_{kl}\rightarrow u,v,\zeta_x,\zeta_y$でIFFT4回と$(u\zeta_x+v\zeta_y)\rightarrow F_{kl}$のFFT1回：合計5回

変形後

$a_{kl}\rightarrow u,v$でIFFT2回と$uv\rightarrow A_{kl},v^2-u^2\rightarrow B_{kl}$のFFT2回：合計4回

aliasing誤差の除去

　2次元における2次の非線形項の変換法による評価でどのようなaliasing項が表れるかを確認し，そのaliasing項の除去方法について述べる⁷⁶⁸⁹．

aliasing項

　例として$w(x,y)=u(x,y)v(x,y)$の評価を考える．$u,v$を有限なフーリエ級数で展開し，展開係数$\hat{u}$, $\hat{v}$を定義する．
$\hat{u},\hat{v}\rightarrow \boxed{{\rm IFFT}} \rightarrow u,v\rightarrow w\rightarrow \boxed{{\rm FFT}} \rightarrow \hat{w}$を考える.

\begin{align}
&u(x_m,y_n)=u_{mn}=\sum_{k=-N/2}^{N/2-1}\sum_{l=-N/2}^{N/2-1}
\hat{u}_{kl}e^{ikx_m}e^{ily_n},\\
&v(x_m,y_n)=v_{mn}=\sum_{k=-N/2}^{N/2-1}\sum_{l=-N/2}^{N/2-1}
\hat{v}_{kl}e^{ikx_m}e^{ily_n}.\tag{20}
\end{align}

$w_{mn}=u_{mn}v_{mn}$より，物理空間の格子点上で得られた$w_{mn}$を2次元DFTすれば，$\hat{w}_{kl}$が得られるように思える．しかし実際にはaliasing項による誤差が生じる．

\begin{align}
\widetilde{w}_{kl}
=\frac{1}{N^2}\sum_{m=0}^{N-1}\sum_{n=0}^{N-1}
w_{mn}e^{-ikx_m}e^{-ily_n}\\
\end{align}

上式に式(20)を代入する．

\begin{align}
\widetilde{w}_{kl}
=\frac{1}{N^2}\sum_{m}\sum_{n}\sum_{k_1}\sum_{k_2}\sum_{l_1}\sum_{l_2}
\hat{u}_{k_1l_1}\hat{v}_{k_2l_2}e^{i(k_1+k_2-k)x_m}e^{i(l_1+l_2-l)y_n}\tag{21}
\end{align}

各$\sum$の範囲は省略した．ここで，$e^{ikx_m}$について考える．式(11)の格子点座標の定義を代入すると，

\begin{align}
\sum_{m=0}^{N-1}e^{ikx_m}
=
\sum_{m=0}^{N-1}\exp\left(ik\frac{2\pi }{N}m\right)
=
\sum_{m=0}^{N-1}\exp\left(\frac{2\pi ik}{N}m\right)\tag{22}
\end{align}

初項$1$，公比$r=\exp(2\pi ik/N)$，項数$N$の等比級数とみなせる．よって，等比級数の和の公式より

\begin{align}
\sum_{m=0}^{N-1}e^{ikx_m}
=
\begin{cases}
0& r\ne1\\
N& r=1
\end{cases}
\end{align}

当然$e^{ily_n}$も同様に考えられる．$C_1,C_2$を整数として

\begin{align}
k_1+k_2-k=C_1N,\;\;l_1+l_2-l=C_2N
\end{align}

の場合のみ値を持つ．$k,l$の取りうる範囲から，$C$の取りうる範囲は，$C_1,C_2=0,\pm1$．結局，次のように書き下すことができる．

\begin{align}
\widetilde{w}_{kl}
&=\sum_{C_1,C_2=0,\pm1}\sum_{k_1,k_2,l_1,l_2}
\hat{u}_{k_1l_1}\hat{v}_{k_2l_2}
\delta_{k_1+k_2-k,C_1N}\delta_{l_1+l_2-l,C_2N}\\
&=\sum_{C_1,C_2=0,\pm1}\sum_{k_1+k_2-k=C_1N,\\l_1+l_2-l=C_2N}
\hat{u}_{k_1l_1}\hat{v}_{k_2l_2}\\
&=\sum_{k_1+k_2-k=0,\\l_1+l_2-l=0}
\hat{u}_{k_1l_1}\hat{v}_{k_2l_2}
+\sum_{k_1+k_2-k=\pm N,\\l_1+l_2-l=0}
\hat{u}_{k_1l_1}\hat{v}_{k_2l_2}
+\sum_{k_1+k_2-k=0,\\l_1+l_2-l=\pm N}
\hat{u}_{k_1l_1}\hat{v}_{k_2l_2}
+\sum_{k_1+k_2-k=\pm N,\\l_1+l_2-l=\pm N}
\hat{u}_{k_1l_1}\hat{v}_{k_2l_2}\tag{23}
\end{align}

第一項が求めたい$\hat{w}$で，第二,三項がsingle-aliased contributions，第四項がdouble-aliased contributionと呼ばれる⁷．

de-aliasing method

　式(23)で表れた3つのaliasing項を取り除く．
$$
-N<k_1+k_2-k<N,;;;-N<l_1+l_2-l<N\tag{24}
$$
この二つの条件を満たせば良い．つまり，$k_1,k_2,k,l_1,l_2,l$の絶対値が大きくなると条件式(24)が満たされない可能性がある．よって，絶対値の大きな波数に対する成分を強制的に$0$とすれば良い．ここで，非線形項を評価する物理空間の自由度を変えずフーリエ空間の有効自由度を減らす方法を2/3-rule．物理空間の自由度を増やしてフーリエ空間の自由度を保つ方法を3/2-rule​と呼ぶ．

2/3-rule

$-N'\leq k_1,k_2,k,l_1,l_2,l\leq N'$ならば式(24)を満たすと考えると，
$${\rm Max}(k_1+k_2-k,l_1+l_2-l)=3N'$$
$${\rm Min}(k_1+k_2-k,l_1+l_2-l)=-3N'$$
より，$3N'<N$ならば良い．最大有効波数は$N'=N/3=(2/3)\cdot(N/2)$となるので，2/3-ruleと呼ばれる．展開係数$\hat{u}$,$\hat{v}$を次の条件で打ち切ってからIFFTで$u,v$を求め，その積$w$をFFTにかければ，$\hat{w}=\widetilde{w}$となる．

\begin{align}
\hat{u}_{kl},\hat{v}_{kl}=0\;\;\; {\rm if}\;\;|k|>N/3 \cup|l|>N/3
\end{align}

この手法では，計算量はほぼ増加しないことがメリットであり，フーリエ空間の自由度が減少することがデメリットである．

3/2-rule

　フーリエ空間での自由度が$N^2$であることを担保したい．2/3-ruleとは逆に，$-N/2\leq k,l\leq N/2-1$の区間の外側に$0$成分を付加して，aliasing項が表れないようにする．必要な$0$成分の範囲は,
$$
\begin{align}
-N'<\frac{3}{2}N-1\leq k_1+k_2-k,l_1+l_2-l\leq\frac{3}{2}N-2<N'
\end{align}
$$
よって$N'=3N/2$として，次図で示す中心部の緑色の領域を除く赤線で囲まれた領域を0詰めした展開係数$\hat{u}_{k'l'}$

\begin{align}
\hat{u}_{k'l'}=
\begin{cases}
\hat{u}_{kl}\:\:&-N/2\leq k,l\leq N/2-1\\
0&{\rm otherwise}
\end{cases}\\
(-3N/2\leq k',l'\leq 3N/2-1)
\end{align}

を用いて，自由度$(3N/2)^2$の2次元IFFTで$u_{m'n'},v_{m'n'}$を求める．ここで$m',n'$の範囲は$0\leq m',n'\leq 3N/2-1$である．$w_{m'n'}=u_{m'n'}v_{m'n'}$を求めて，自由度$(3N/2)^2$の2次元FFTで$\widetilde{w}$を求める．求めたい$\hat{w}$はその一部で，

\begin{align}
\hat{w}_{kl}=\widetilde{w}_{kl}\;\;(-N/2\leq k,l\leq N/2-1)
\end{align}

となり，$\widetilde{w}_{kl}$の残りの成分の情報は捨てることになる．この手法のメリットは，フーリエ空間の自由度が減少しないことであり，デメリットは計算コストの増加である．今回はこちらの手法を用いる．

時間積分法

　古典的な4段4次精度Runge-Kutta法と積分因子法(integrating factor technique)⁷を組み合わせて時間積分を行う¹¹⁰．

4段4次Runge-Kutta法

　次の微分方程式を4段4次のRunge-Kutta法を用いて積分することを考える．
$$
\begin{align}
\frac{df}{dt}=\mathcal{F}(t,f)
\end{align}
$$
時刻$t^n$で$f=f^n$とすると，$t^{n+1}=t^n+\Delta t$における$f^{n+1}$は次の様に評価できる．

\begin{align}f^{n+1}&=f^n+\frac{1}{6}\left(k_1+2k_2+2k_3+k_4\right)+\mathcal{O}(\Delta t^5)\tag{25}\\k_1&=\Delta t\mathcal{F}(t^n,f^n)\\k_2&=\Delta t\mathcal{F}(t^n+\frac{1}{2}\Delta t,f^n+\frac{1}{2}k_1)\\k_3&=\Delta t\mathcal{F}(t^n+\frac{1}{2}\Delta t,f^n+\frac{1}{2}k_2)\\k_4&=\Delta t\mathcal{F}(t^n+\Delta t,f^n+k_3)\\\end{align}

積分因子法

　次の微分方程式を考える．
$$
\begin{align}\frac{df}{dt}=\mathcal{F}(f)-\alpha f\end{align}
$$
ここで$\mathcal{F}(f)$は$f$に関する非線形関数，$\alpha$は定数係数である．これは以下の様に式変形できる．

\begin{align}\frac{df}{dt}+\alpha f&=\mathcal{F}(f)\\\left(\frac{df}{dt}+\alpha f\right)e^{\alpha t}&=\mathcal{F}(f)e^{\alpha t}\tag{26}\\\end{align}

この形のもとで，時間微分を差分化するのが積分因子法 (Integrating factor technique) である．例えば，1次精度のEuler陽解法を用いると次式のようになる．
$$
f^{n+1}=e^{-\alpha \Delta t}\left(f^n+\Delta t\mathcal{F}(f^n)\right)
$$

RK法と積分因子法の組み合わせ

　式(26)に式(25)を用いると，次のように時間微分を差分化できる¹¹⁰．

\begin{align}f^{n+1}&=e^{-\frac{\alpha}{2}\Delta t}\left(e^{-\frac{\alpha}{2}\Delta t}(f^n+\frac{1}{6}k_1)+\frac{1}{3}(k_2+k_3)\right)+\frac{1}{6}k_4+\mathcal{O}(\Delta t^5)\\k_1&=\Delta t\mathcal{F}\left(t^n,f^n\right)\\k_2&=\Delta t\mathcal{F}\left(t^n+\frac{1}{2}\Delta t,e^{-\frac{\alpha}{2}\Delta t}\left(f^n+\frac{1}{2}k_1\right)\right)\\k_3&=\Delta t\mathcal{F}\left(t^n+\frac{1}{2}\Delta t,e^{-\frac{\alpha}{2}\Delta t}f^n+\frac{1}{2}k_2\right)\\k_4&=\Delta t\mathcal{F}\left(t^n+\Delta t,e^{-\frac{\alpha}{2}\Delta t}\left(e^{-\frac{\alpha}{2}\Delta t}f^n+k_3\right)\right)\\\end{align}

なお，線形項 ($\alpha f$) の評価を常に$\frac{\Delta t}{2}$の時間刻み幅で行うために，文献¹⁰の式を若干変形している．

計算例

　3つの計算例を示す．共通して自由度$N=2^{10}$，4並列で計算した．Paraview⁴を用いて渦度を可視化した．

###Kelvin-Helmholtz不安定性

demo01	Kelvin-Helmholtz不安定性
$\nu$	$0$（=非粘性)
$\Delta t$	$5.0e-3$
$t_{end}$	20
total step	4000
計算時間	約12分

初期条件

\begin{align}
\zeta(x,y)=&4.0\left\{
\exp\left[-(20x-10\pi)^2\right]\cdot(1+0.01\cos(2.0(y+0.5\pi))\\
-\exp\left[-(20x-30\pi)^2\right]\cdot(1+0.01\cos(2.0(y+0.5\pi))
\right\}
\end{align}

可視化

###同符号の渦の合体
文献¹にある計算例を用いた．

demo02	同符号の渦の合体
$\nu$	$2.0e-6$
$\Delta t$	$2.0e-2$
$t_{end}$	100
total step	5000
計算時間	約15分

初期条件

\begin{align}
\zeta(x,y)=\;\;&
\exp\left[\left(\cos(x-x_1)+\cos(y-y_1)-2\right)/\sigma^2\right]\\
-&\exp\left[\left(\cos(x-x_2)+\cos(y-y_2)-2\right)/\sigma^2\right]-C\\
\end{align}

なお定数は以下の通り与える
$$
\sigma=\pi/10,;;x_1=y_1=0.8\pi,;;x_2=y_2=1.2\pi,;;C=0.0322447
$$

可視化

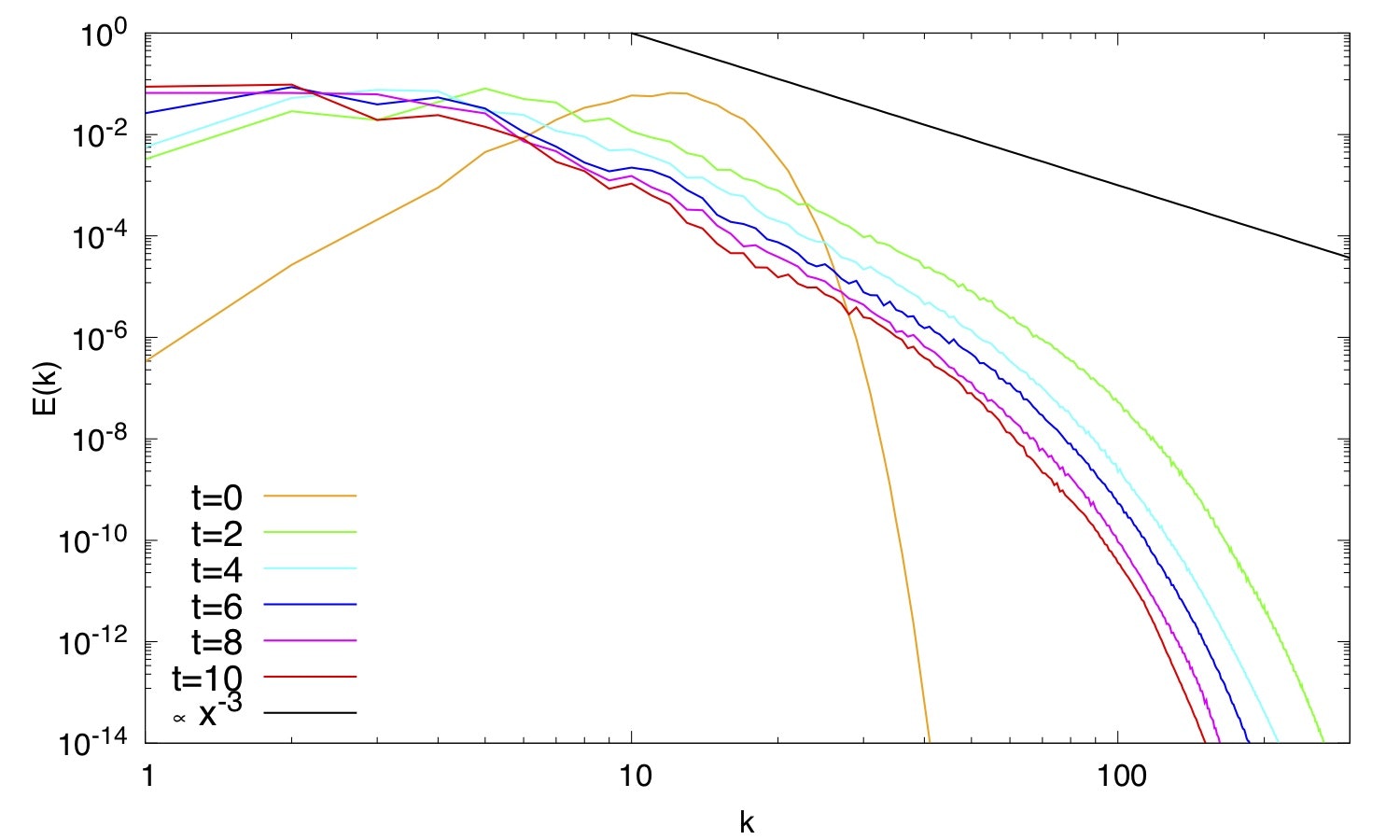
###2次元等方性乱流の減衰

San,O.,Staples,A.E.¹¹の数値実験(6. Two-dimensional decaying turbulence)を行う．

demo02	2次元乱流の減衰
$\nu$	$1.0e-3$
$\Delta t$	$2.0e-4$
$t_{end}$	10
total step	50000
計算時間	約2.5時間

初期条件

San,O.,Staples,A.E.¹¹と同様

可視化

エネルギースペクトル

ソースコード

　上で示した3つの計算例を含むソースコードはGithubで公開している．

https://github.com/toya42/psm4cfd

　本プログラムの特徴は，次のようにまとめられる．

• 安全で移植が容易な記法で実装 (Fortran2008．macOS&Ubuntuで動作確認)
• 高速なFFT (Intel MKLの利用）
• 並列計算が可能（スレッド並列：対応，プロセス並列：未対応）
• 大きな自由度の計算も可能（コンパイルオプションの変更だけで$N\geq 2^{14}$に対応）
• MITライセンスで公開（自由に使ってください）

Intel MKL以外のFFTライブラリを使用したい場合

　fft2d_mkl.F90を置き換えれば良い．入出力は一般的なCCE形式¹²なので，FFTW¹³などへの変更は容易だと思われる．

終わりに

　スペクトル法で非圧縮性流体の2次元周期流を計算するプログラムを作成した．V&Vが不十分，プロセス並列に未対応等と課題は残っているが，せっかくなのでGithubで公開した．

　今後の予定としては

• 3次元周期流
• 2次元ポアズイユ流
• 3次元チャネル乱流

に挑戦したいと考えている．

1. 石岡圭一(2004)『スペクトル法による数値計算入門』東京大学出版会 ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶ ↩⁷ ↩⁸

2. C. Canuto, M. Y. Hussaini, A. Quarteroni, T. A. Zand, Specral Methods Fundamentals in Single Domain, Springer-Verlag (2006). ↩

3. Intel Math Kernel Library (https://software.intel.com/en-us/mkl) ↩

4. Paraview (https://www.paraview.org/) ↩ ↩²

5. 大宮司久明 (2009) 『数値流体力学大全』(http://www.caero.mech.tohoku.ac.jp/publicData/Daiguji/) 『第12章　非圧縮性流れの解法―渦度輸送方程式と流れ関数方程式を解く方法』(http://www.caero.mech.tohoku.ac.jp/publicData/Daiguji/Chapter12.pdf) ↩ ↩² ↩³

6. 木田重雄，柳瀬眞一郎 (1999) 『乱流力学』朝倉出版 ↩ ↩² ↩³

7. C. Canuto, M. Y. Hussaini, A. Quarteroni, T. A. Zand, Specral Methods Evolution to Complex Geometries and Applications to Fluid Dynamics, Springer-Verlag (2007). ↩ ↩² ↩³

8. 中央大学理工学研究科物理学専攻中野研究室　講義資料 (https://www.phys.chuo-u.ac.jp/labs/nakano/tokuron2/sec61(08).pdf) 2019.09.04閲覧 ↩

9. 岐阜大学准教授　田中雅宏（2006） 講義配布資料のまとめ　(https://www1.gifu-u.ac.jp/~tanaka/numerical_analysis.pdf) 2019.09.04閲覧 ↩

10. 北川真帆，村上洋一．数理解析研究所講究録(2012), 1800:226-235，京都大学数理解析研究所，https://repository.kulib.kyoto-u.ac.jp/dspace/handle/2433/173013 ↩ ↩² ↩³

11. San,O.,Staples,A.E.:High-order methods for decaying two-dimensional homogeneous isotropic turbulence. Comput. Fluids 63, 105–127 (2012) ↩ ↩²

12. Developer Reference for Intel® Math Kernel Library - Fortran DFTI_PACKED_FORMAT (https://software.intel.com/en-us/onemkl-developer-reference-fortran-dfti-packed-format), fortranに関するメモ FFT(http://www.ton.scphys.kyoto-u.ac.jp/~michikaz/fortran.html#level5) 等 ↩

13. FFTW (http://www.fftw.org/) ↩