AtCoder ABC418 振り返り(PythonでABCD問題)

ABC418を振り返ります

今回はABCDまで4問解答(3回誤答)でした。B問題で1回、D問題で2回の誤答がありました。レーティングは微増でした。

A - I'm a teapot

pythonでは、endswithを使うと文字列の末尾が特定の文字列で終わっているかどうかを簡単に確認できます。

N = int(input())
S = input()

is_tea = S.endswith('tea')
print('Yes' if is_tea else 'No')

http のステータスコード 418 が "I'm a teapot" ということから来ている問題ですね。

B - You're a teapot

Sを探索していき、"t"だったら、それ以降の文字を探索します。充填率というのが聞き慣れない単語ですが、問題文に書いてある通りに計算します。

S = input()
answer = 0

# 文字列Sを探索
for i in range(len(S) - 1):
    # "t" の文字を見つけたら,そこから後ろを探索
    if S[i] == 't':
        t_count = 1
        # "t" の後ろの文字を探索
        for j in range(i + 1, len(S)):
            if S[j] == 't':
                t_count += 1
            # 充填率を計算し、最大の充填率を更新
            if j - i > 1 and S[j] == 't':
                precent = (t_count - 2) / ((j - i + 1) - 2)
                answer = max(answer, precent)
print(answer)

C - Flush

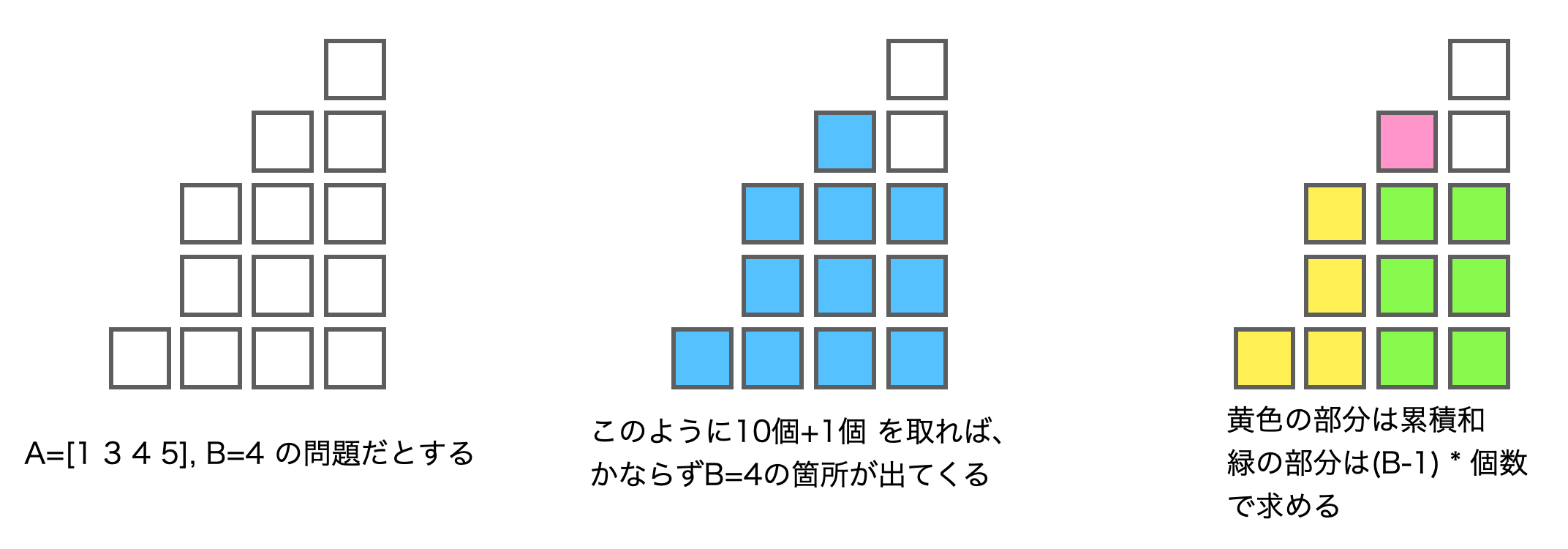
これは結構悩ましい問題でした。図に書くとわかりやすいので、図で説明します。

B=4の場合、ディーラー視点では以下のような行動をすると、最も多くなります。

• 在庫が3個以下のティーバッグ → 在庫を全部出す
• 在庫が4個以上のティーバッグ → 3個まで出す

というわけで、これを二分探索と累積和を使って求めました。

N, Q = map(int, input().split())
A = list(map(int, input().split()))

# Aの要素をソートしておきます
A.sort()

# Aの累積和を計算しておきます
sum_a = []
sum_a.append(0)  
for i in range(len(A)):
    sum_a.append(sum_a[-1] + A[i])

# Aの最大値を求めておきます
max_a = max(A)

for i in range(Q):
    B = int(input())
    # BがAの最大値より大きい場合は、-1を出力
    if B > max_a:
        print(-1)
        continue
    
    # 初めてB以上の値が出てくる位置を二分探索で求めます
    idx = bisect.bisect_left(A, B)

    # idxより左側の累積和 + idx以上の要素の数 + 1
    answer = sum_a[idx] + (len(A) - idx) * (B - 1) + 1
    print(answer)

D - XNOR Operation

長さN+1の文字列があったら、[N個の文字] + [1個の文字] と分解して考えると、最終的に 0 になるか 1になるかがわかります。

# 111: [11] と [1] に分解できて、[11]は 1 なので
111 → [11][1] → 11 → 1 

# 1110: [111] と [0] に分解できて、[111]は 1 なので
1110 → [111][0] → 10 → 0 

DP(動的計画法)で解きます。以下の2つのパターンを考えます。
・i文字目までで、最終的に0になる部分文字列の数
・i文字目までで、最終的に1になる部分文字列の数

これを最後まで求めていき、各iでの部分文字列の数を合計します。

N = int(input())
T = input()

dp = [[0] * 2 for _ in range(N + 1)]
count = 0
for i in range(N):
    # 既存の部分文字列に、ひと文字T[i]を追加すると考える
    if T[i] == "0":
        # 0を追加した場合
        dp[i + 1][0] = dp[i][1] + 1 # 左側の文字列が1なら、0を追加すると0になる
        dp[i + 1][1] = dp[i][0]     # 左側の文字列が0なら、0を追加すると1になる
        count += dp[i + 1][1]
    else:
        # 1を追加した場合
        dp[i + 1][0] = dp[i][0]     # 左側の文字列が0なら、1を追加すると0になる
        dp[i + 1][1] = dp[i][1] + 1 # 左側の文字列が1なら、1を追加すると1になる
        count += dp[i + 1][1]

print(count)

本番ではDPを使わないで解こうとしてしまい、TLEで2ミスでした。