先日リリースされたドラゴンクエストウォーク、やってます? DQ 1, 2, 3 世代の私は、いつか強い武器が買えるようになるんだろうなと思いながらレベル 35 まではがねの剣で頑張っていました。最近の風習では武器はガチャで手に入れるものなんですね。このような RPG の戦闘シーンは VRF (Verifiable Random Function) を使う説明の良い例になるだろうな思いながら、いい機会なのでいつか書こうと思っていた VRF に関する記事を投稿します。
TL;DR
- VRF を使うと作為的な選択や偽造ができない乱数をアプリ (クライアント) 側に発生させることができる。
- その乱数に基づいて決定性アルゴリズムでシーンを判断してゆけば、アプリ側でモンスターを作為的に選んだり、ありえない経験値を叩き出すような行為を試みてもサーバ側で不正であると判断することができる。
- 結果的に、サーバ側の処理をアプリ側に安全に委譲できるのでサーバの負荷を削減しシステムコストを下げる事ができる。
Verifiable Random Function
VRF は暗号論的疑似乱数生成アルゴリズムです。理想的な VRF はランダムオラクルモデルのハッシュ関数、つまり現実的には SHA3-256 のような暗号論的ハッシュ関数と考えることができます。一般的なハッシュ関数と異なる点はハッシュ値の生成に非対称鍵アルゴリズムを使用していることです。つまりハッシュ値を得た第三者が、その公開鍵に対応する秘密鍵を使ってしか作り得ない値である (ハッシュ値の生成者に都合の良い値が偽造されていたり、作為的に選択されたものではない) ことを検証することができます。これを破るには暗号論的困難さを伴います。
形式的にはハッシュ関数や共有鍵を使用する HMAC と似ていて、その公開鍵バージョンが VRF とも言えます。
| アルゴリズム | 形式 |
|---|---|
| ハッシュ関数 | ${\rm HASH}: m \to h$ |
| HMAC | ${\rm HMAC}: (S,m) \to h$ |
| VRF | ${\rm VRF_{hash}}: (S_k,m) \to (\pi,h)$ ${\rm VRF_{verify}}:(P_k,m,\pi,h) \to \ {\it VALID} \ \mbox{or not}$ |
このセクションの残りの部分では公開鍵ペア $(S_k,P_k)$ をそれぞれある主体 $k$ の秘密鍵、公開鍵と仮定し、VRF を使用してあるメッセージ $m$ に対するハッシュ値 $h$ を生成 (つまり乱数シードを指定した暗号的疑似乱数の算出に相当) し、またそれを検証する方法を紹介します。
ハッシュ値と証明の算出
暗号論的疑似乱数として使用できるハッシュ値 $h$ は、秘密鍵 $S_k$ とメッセージ $m$ を使用して以下の基本的な 2 つの関数を使用して算出することができます:
${\rm prove}: (S_k, m) \to \pi$
${\rm proof\_to\_hash}: \pi \to h$
この記事ではこれらの 2 関数を組み合わせて以下のように略記します。
${\rm hash}: (S_k,m) \to (\pi, h)$
ここで $\pi$ は証明と呼ばれ、ハッシュ値が確かに秘密鍵 $S_k$ を使って生成されたことを示す情報として使用します (証明自体に疑似乱数の性質はありません)。
ハッシュ値と証明の検証
証明 $\pi$ が確かにメッセージ $m$ から秘密鍵 $S_k$ によって生成されたものであることは以下の関数を使用して検証することができます:
${\rm verify}: (P_k,\pi,m) \to \mbox{true or false}$
また前述の関数を使用して証明 $\pi$ からハッシュ値を生成できるため、検証の済んだ $\pi$ からハッシュ値 $h$ を復元することは可能です。
${\rm proof\_to\_hash}: \pi \to h$
ただし、実際のシステムでは $h$ を使用するすべてのプログラムがコストの高い proof_to_hash() を実行しなくてもよいように、多くのケースでは $(\pi,h)$ をセットで扱います。この場合の検証は verify(pk,pi) && proof_to_hash(pi) == h の判定で行います (これを ${\rm verify}$ と考えても良い)。
直感的な理解と代用方法
勘のいい人は気づいた思いますが、この VRF のハッシュ値生成と検証は一般的な電子署名とハッシュ関数を使用して構成することもできます。つまり証明 $\pi$ を電子署名と考えて、${\rm prove}$ を電子署名生成、${\rm verify}$ を電子署名検証、${\rm proof\_to\_hash}$ を SHA3-256 のようなハッシュアルゴリズム、または暗号論的疑似乱数生成アルゴリズムと考えて代用が可能です。この振替手段は計算効率が劣るものの、もし実行環境で VRF 実装が利用できないようなケースであれば考慮しても良いと思います。
もしそうでないとしても、機能的に電子署名とハッシュ関数の組み合わせだと考えるとで VRF の理解を助ける手がかりになると思います。
VRF の特徴
- 一般的なハッシュ関数と同様に、入力メッセージ $m$ に対してどのようなハッシュ値 $h$ が生成されるかは ($m$ の生成者であっても、秘密鍵 $S_k$ の持ち主であっても) 意図的に操作することができない。つまり、乱数の生成側が作為的な乱数を生成したり選ぶことは暗号論的な困難さを伴う。
- ただし、公開鍵ペア $(S_k,P_k)$ がメッセージ $m$ より先に生成され公開鍵が共有されている場合に限る。そうでなければ $m$ に対して都合の良い乱数を生成する鍵を選択することができる。
- $h$ が $k$ の秘密鍵によって生成されたハッシュ値であることを第三者が検証できる。これにより当選権利を持たないのに当たったと主張するようなことを排除することができます。
ではこれらができることで何に応用が可能なのかを次のセクションで RPG の戦闘を設計してみたいと思います。
RPG の戦闘モデル設計
スマートフォン上のアプリでプレイする RGP ゲームの 1 回の戦闘シーンについて考えます。
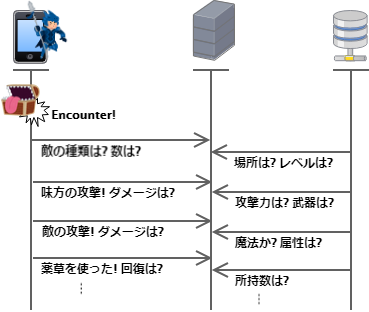
高頻度インタラクションの問題
プレーヤーや敵が何かアクションを起こすたびにサーバに問い合わせていると、システム全体としての整合性は保証はできるかもしれませんが、当然ながらネットワークとサーバ、DB の負荷が膨大になりますよね。またこのようにサーバ依存度が高いと電車がトンネルに入ったとたんに戦闘が止まってしまうようなことも起きて UX は非常に低いものになります。
とはいえ、どんな敵に遭遇してどんなアクションをしてどんなゴールド/経験値/アイテムを獲得するかをすべてをアプリ側で決定する設計では、不正に手を染めてでも実績やレアアイテムを入手したいチーター、またアカウントやアイテムを売ろうとする RMT 業者の間で不当に改造されたバイナリが出回るかもしれません。
VRF と決定性アルゴリズムによる処理の委譲
VRF を使ってアプリ側で処理が完結しながらこれらの不正行為をサーバ側で検証できるような設計を考えてみましょう。この方法は何度も乱数を再作成しますので、暗号理論ほど強固ではないがより軽い疑似乱数関数 ${\rm rand:x \to y}$ を追加します。
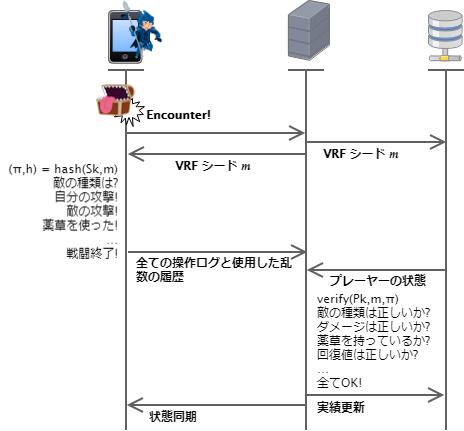
- アプリは秘密鍵 $S_k$ を持っており、サーバにその公開鍵 $P_k$ が共有されているものとします。また疑似乱数関数
rand()もアプリとサーバで共有されています。 - 戦闘シーンが始まると、サーバは VRF シード $m$ を生成して保存しアプリに送信します。
- アプリはシード $m$ と自分の秘密鍵 $S_k$ から証明 $\pi$ と乱数 $h$ を生成します。
- まず敵の種類と倒した時の実績値を決めます。
- 単純化のために 100 種類のモンスターが同じ確率で出現すると仮定してインデックス
rand(h+1) % 100のモンスターと遭遇したことにします。 - 先に実績値を決めましょう。経験値を
rand(h+2) % 1000、ゴールドをrand(h+3) % 1000、アイテムをドロップするかをrand(h+4)÷RAND_MAX < 0.001、何をドロップするかを 20 種類の中からrand(h+5) % 20で選択します。 - 先手のプレーヤーが攻撃を選んだのでダメージを決定します。これも単純化のため 0~99 の間で一様の確率で決まるとすると
rand(h+6) % 100のダメージを与えたことにします。 - 後手の敵の攻撃も同様に
rand(h+7)に基づいた乱数からダメージを決定します。 - プレーヤーが薬草を使いました。
rand(h+8)に基づいた乱数から回復値を決定します。 - 以後、(もっと良い方法があるかもしれないが)
rand()を呼び出すたびにhの加算値を増やして新しい乱数を生成し、その乱数に応じた結果のシナリオを適用してゆきます。 - 戦闘が終了してプレーヤーは最初に算出した実績値を手に入れました。最後に、$\pi$, $h$ とすべての操作手順、使用した乱数、その結果をまとめてサーバに送信します。
この操作で重要なことは、ゲーム性を出すためのランダムさを混入させてはいるものの、すべて決定性アルゴリズムで行われているという点です。したがって、サーバは自分の発行した $m$ に基づいて $k$ が生成した $h$ であること、つまりアプリに都合の良い値を作為的に選択した乱数でないことが確認できれば、戦闘の残りのすべての手順とその結果が正当であるかを 1 ユニット分まとめてバッチ処理的に検証することができます。
長所や短所の考察
この設計の長所は主にシステムパフォーマンスや負荷に関する部分です。
- アプリとサーバ間のインタラクションが削減できる。
- 戦闘中の通信が削減されてパフォーマンスが向上する。
- スマートフォンの通信量が減る。
- 通信状況が悪い場所でも著しい UX 低下を引き起こさない。
- サーバ側で保持する情報はシード $m$ だけ。
- 戦闘セッション中のサーバ側ストレージ負荷が低い。
- サーバ側のセッション維持コストは殆どないので戦闘中に放置されても何十時間でも待っていられる。
- 戦闘セッション中のサーバ側ストレージ負荷が低い。
- 操作手順をまとめて処理/検証できる。
- 1 ステップごとに処理するよりパフォーマンスが向上する。
- Spark のようなバッチ型分散処理の導入でスケールできる。
- 操作の時系列を考慮した分析や不正検知が実装しやすい。
- お互いに相手の不正の監視ができる
- アプリやプレーヤー側からしてみれば、ゲームベンダーが不当な確率調整、実績調整をしていないことを検証できる。
- ゲームベンダー側からしてみれば、不正なバイナリを使って想定外の実績を不当に入手しようとしていないことを検証できる。
不正行為について考慮しておくポイントがあります。各ステップの判断が決定性アルゴリズムであったとしてもプレーヤーがどのような操作を選択するかは (有限ですが) 非決定的で、不正行為の入り込む余地はその部分と考えられます。つまり、アプリ側で選択肢のシナリオを総当たりで試行し、アルゴリズム的に正しく最も効果の高い選択する行為が考えられます。
前述の例では敵とエンカウントした時点ですべての実績値を決定しました。そうではなく、実績値を一連の操作によってランダムに変えてしまうと (非決定性を持たせてしまうと) 総当たり試行で毎回レアアイテムを引き当てるような選択的操作が可能になってしまいます。一番の不正モチベーションである実績に決定性をもたせることで不正行為者は「いかに効率よく戦闘を終えるか」の観点でしかフォーカスできなくなります。
操作の自動化によるレベル上げ等の行為は VRF で阻止できる範疇ではありません。従来通り、全体的な操作の間隔や行動パターンが手作業として妥当かをサーバ側で判断したり、いっそオートバトルモードをつけて不正に自動化するメリットを下げることが考えられます。
開発のデメリットとしては、似たような処理をアプリ側とサーバ側との両方で実装する必要があるため、仕様が複雑化すると実装やテストの負荷が高くなる点が考えられます。アプリに iOS 版と Android 版が必要な場合はなおさらです。これは処理をアプリ側に分散させネットワークとサーバの負荷を下げる目的に対する課題です。
例えばサービスを提供する企業は仕様と API のみを提供し、複数のアプリの開発ベンダーが自由に参入して API を利用する場合などでは、お互いの不正を検証することができるためメリットとなります。このケースでは生かせませんでしたが、サーバ側とアプリ側の開発主体が異なっていて互いに信用していなくても暗号理論に基づいて機能するという点は VRF の大きな利点の一つです。例えば競技プログラミングのように、ゲーム内でプログラムを作って競わせるような設計であれば、サービスベンダーから作為的に不利な乱数が割り振られないことを保証することは重要な観点です。
あとは延々と戦闘を長引かせると操作ログが巨大化するので 100 ステップで敵が逃げて強制終了するなどの措置が必要ですね。
操作されていない抽選の設計
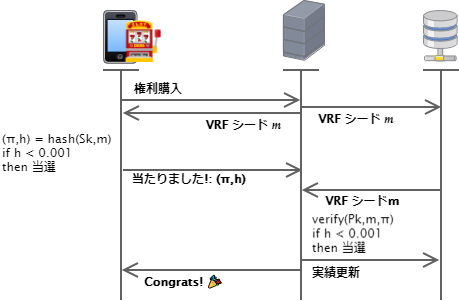
RPG の戦闘ユニットは少し複雑でしたが、スクラッチくじのような設計は VRF の無作為性を利用したもっとも単純化した例です。
シード発行の否認防止のためにシード $m$ には胴元側の電子署名が必要ですが、当選のアルゴリズムと確率が双方に明確に共有されていれば、胴元も購入者も意図的に結果を選ぶことができないので安全な方法といえます。
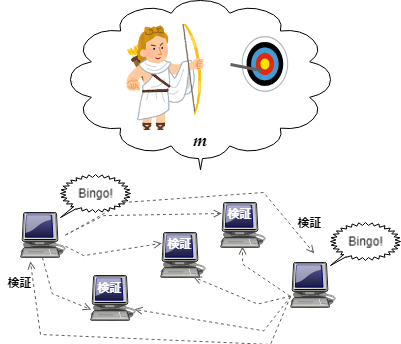
暗号抽選モデルは宝くじのような権利配分や勝敗決定だけではなく、分散システムにおけるリーダー選挙のような役割分担 (指名的または自律的の両方が可能です) でも利用することができます。例えば、すべてのノードが「自然に」共有している、操作や予想ができない何らかのランダムな情報をシード $m$ とすることで、VRF を使用して胴元なしに自分が当選者かを自律的に判断することができます。そして、初手では当選については自分しか知り得ていないわけですから、当選の権利を行使した後で公表することで標的型攻撃を避けることができます。公表後に当選の権利を持っていたことを他のノードが検証することができます。
このような自律性を利用することで、例えば分散 KVS がデータの Sharding を行うときに誰かに指名されることなくても自分の担当するデータのキーを決定できたり、また自分がその担当であることを他のノードに証明することができます。
この構成は Bitcoin のようないくつかのブロックチェーンで使用されれている Proof of Work の計算資源を無駄に消費しない代替手段として使われ始めている方法です。ブロックチェーンの場合は前のブロックのハッシュ値を次のブロック生成者を選ぶためのシード $m$ として使用します。
まとめ
実際の RPG のようなゲームに VRF を適用することは実務的な困難さが伴うでしょうが、無線移動体通信であるスマートフォン上で動作するアプリに固定 PC よりも疎で自律的な動作が求められるのも確かです。自律動作と不正防止の板ばさみとなったときに VRF がヒントの一つになればよいかなと思っています。