この記事について
座標降下法(coordinate descent)によるLassoのスクラッチ実装と、自分なりの数式の解釈を記載しています。
プログラムはPythonで記述しています。
Lassoの回帰式は以下とします。
$$ L=\dfrac {1}{2n}\left|| y-Xw\right|| ^{2}+\lambda \left|| w\right|| _{1} $$
※ \dfrac {1}{2n} の部分は、\dfrac {1}{2} と記載されていることが多い印象ですが、この記事では\dfrac {1}{2n}を前提としています。
参考
Lassoの勉強をするにあたって、主に以下のページ、書籍を参考にさせていただきました。
- Lassoの理論と実装 -スパースな解の推定アルゴリズム-
- リッジ回帰とラッソ回帰の理論と実装を初めから丁寧に
- 機械学習のエッセンス 実装しながら学ぶPython、数学、アルゴリズム
- スパースモデリング - 基礎から動的システムへの応用 -
背景・目的
正則化についての説明でよく見かける下図のグラフに疑問を持ち、Lassoについて知りたくなったというのが背景・目的です。
よく、「LassoはL1ノルムが絶対値なので、パラメータが0になる〜」といった記載と、そのイメージとして下図のようなグラフが掲載されているのを見かけます。
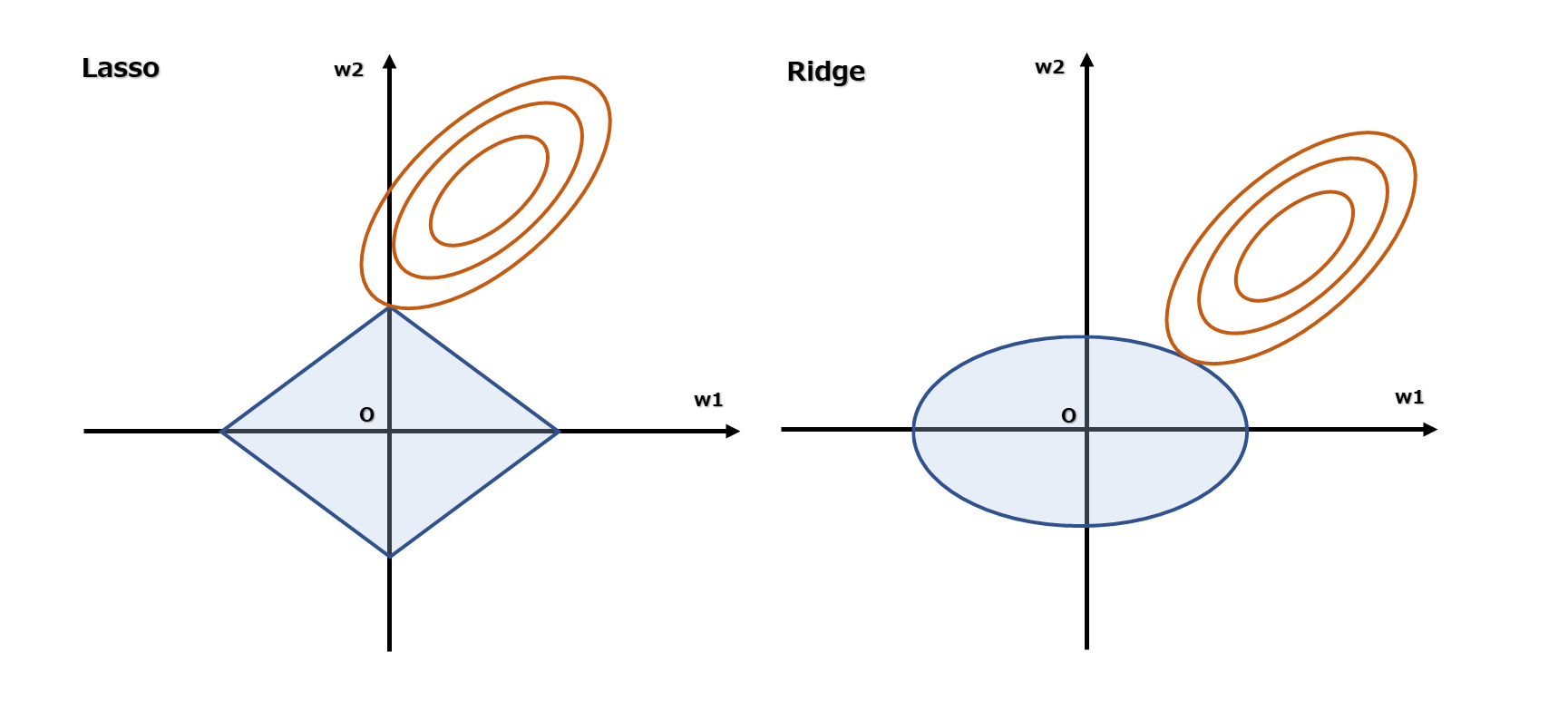
しかし、パラメータが0になること以前に、このグラフの意味することが自分には分かりませんでした。
グラフを理解する
まず、よくあるこの下図のイメージは、説明を簡単にするために重みの数を2つに限定されています。
輪の等高線は誤差を、ひし形は正則化項を表しています。
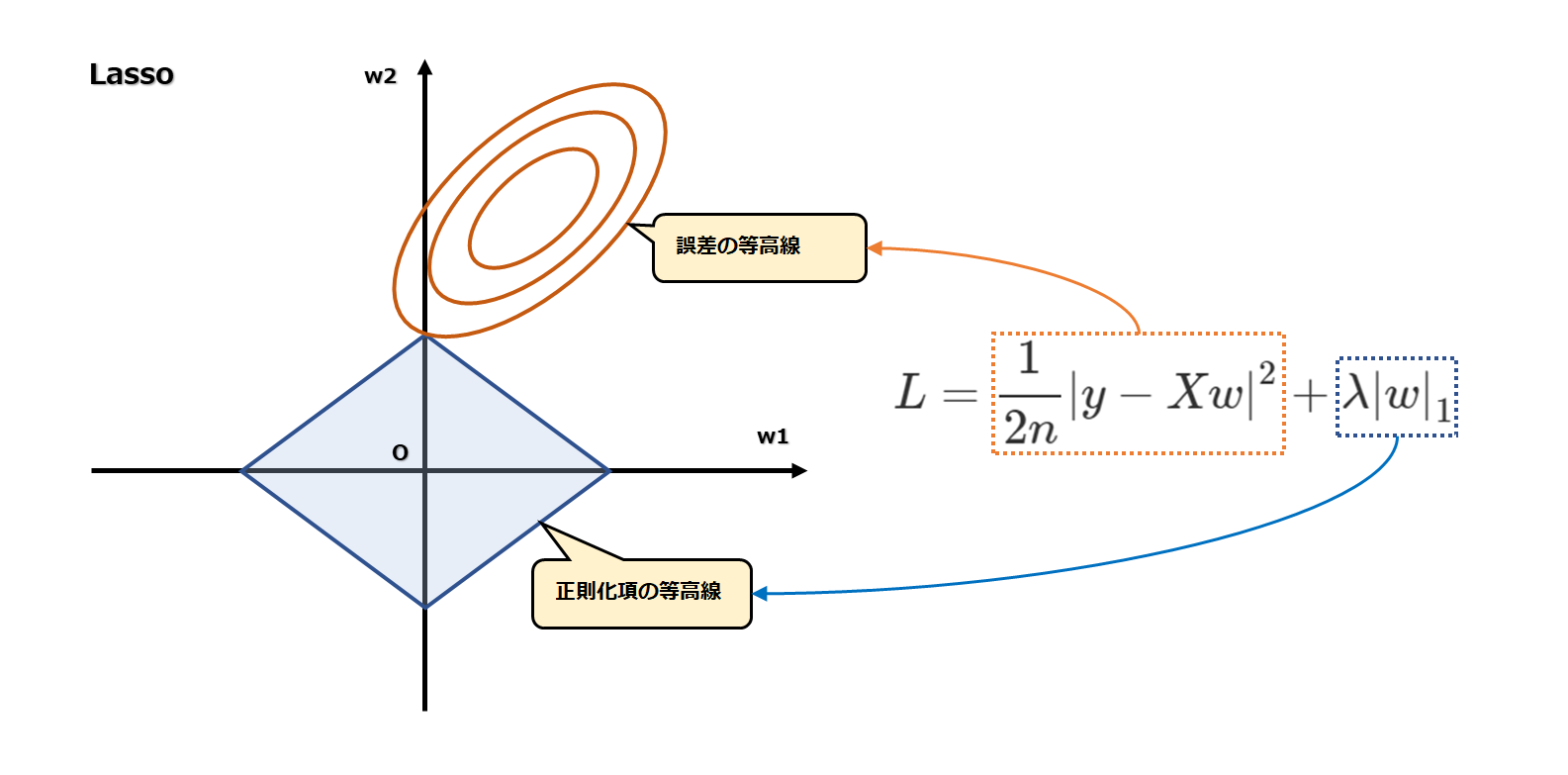
また、この2つの重みにバイアスは含まれていません。
つまり、
$$ y=w_{0}+w_{1}x_{1}+w_{2}x_{2} $$
という回帰式の、w1を横軸、w2を縦軸にした2次元のグラフです。
2次元のグラフですので、誤差を表す3軸目がありません。
そこで、2次元上で誤差を表す手段として、誤差を等高線で表しています。
つまり、等高線の同一の輪の線上にある値(誤差)は、w1、w2が異なる場合でも同じ値であることを意味します。
また、等高線の中心はその式の最小(または最大)を表しています。
等高線は地図上で山の高さを表す際などによく用いられる方法のようです。
等高線で表されている1つの輪の線上は、高さが同じであることを意味します。
また、等高線の中心は山の頂点(山の高さが最大であること)を表していると言えます。
ここで、正則化項がない場合を考えてみます。
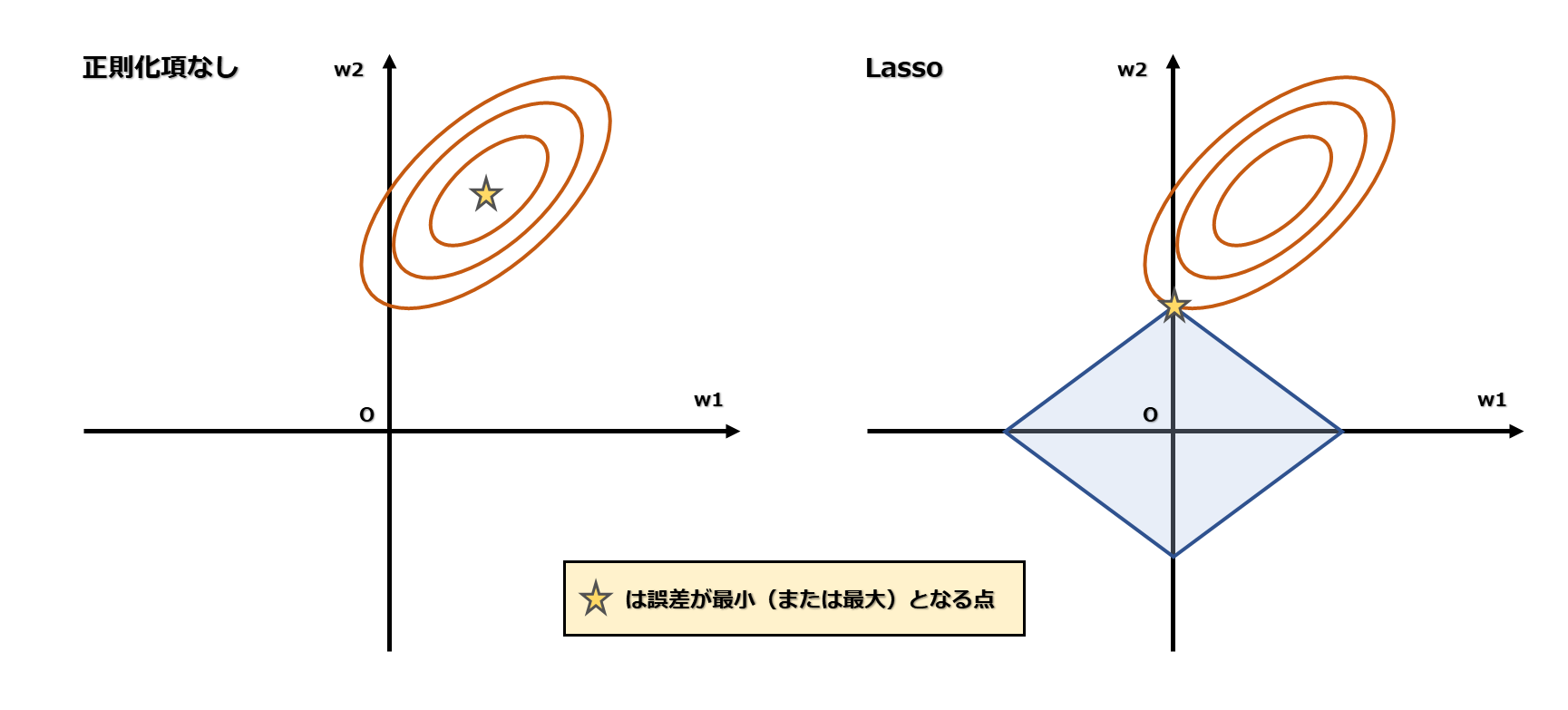
正則化項なしの場合、誤差が最小となる点は、等高線の輪の中心です。
この誤差が最小になるようなw1、w2を求めるのが重回帰の重み算出です。
一方、Lassoはそこに正則化項の制約が加わるため、誤差が最小となる点が正則化項の線上に来ます。
このような制約を与えた上での最小(または最大)を求めることを、制約付き最適化問題と言います。
新たな疑問
グラフの意味はなんとなく理解できましたが、次の疑問が出てきました。
なぜ正則化項の頂点で接しているイメージが多いのでしょうか?
下図のように、頂点でない箇所で接することはないのでしょうか?
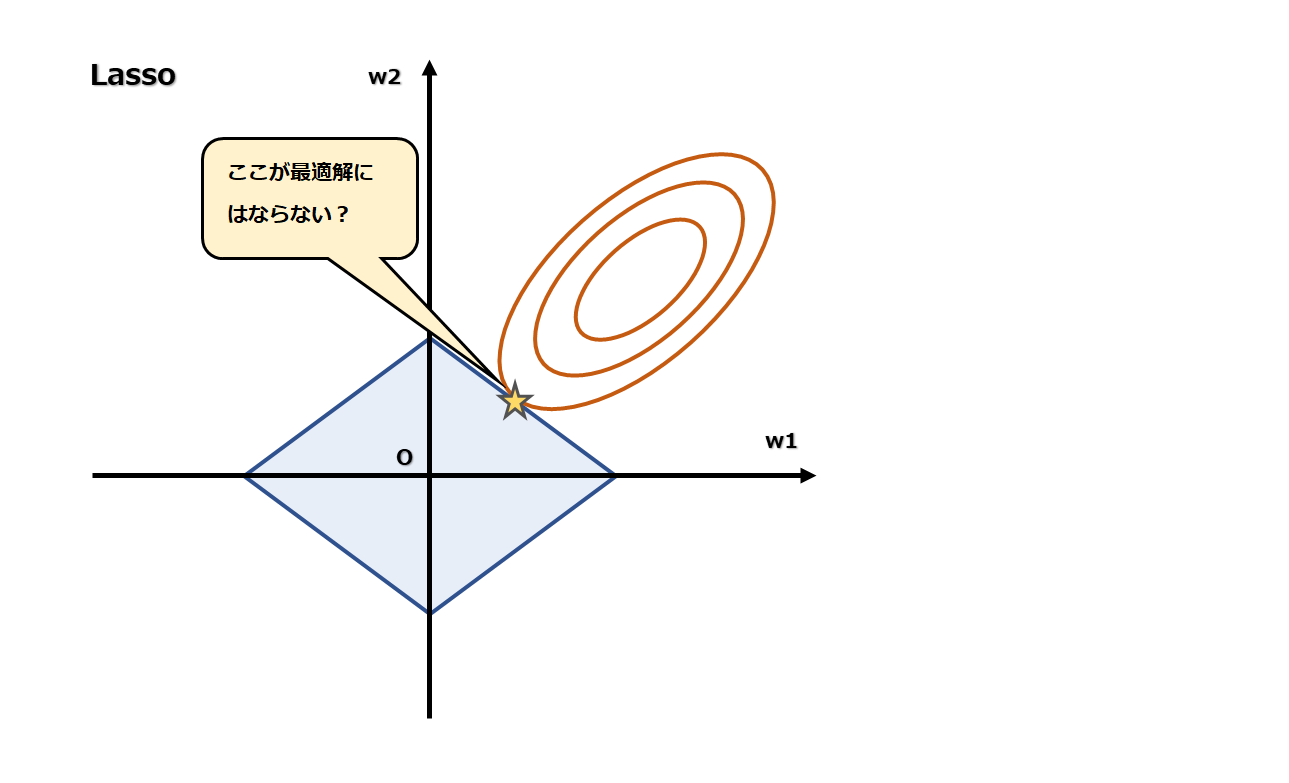
結果から言うと、このようなイメージとなる場合もあります。
ですが、多くの場合、パラメータは0になります。
そもそもLassoの目的から考えると、多くのパラメータが0であることが望ましい、0にしたい、ということが前提にあるように思います。
なので、Lassoのイメージ図としては頂点で接している例が適しているのだと思います。
なぜL1ノルムが用いられるのか
Lassoの正則化項にはなぜL1ノルムが用いられるのでしょうか?
それを考える前にLassoの目的を考えてみます。
Lassoの目的は、「多くの特徴量の中からより少ない特徴量で元の事象を表したい」ということです。
そういった概念をスパースモデリングと呼び、Lassoもその一種です。
“オッカムの剃刀”と呼ばれる、「ある事象を説明するためには、必要以上に多くを仮定すべきでない」という考え方がありますが、スパースモデリングの根底となる考え方として紹介されています。
ではどうやって特徴量を選択すれば良いでしょうか。
「ある式に含まれる要素のそのほとんどはゼロである」と仮定します。
そうした場合、非ゼロな要素はどれだろう?ということを求めたくなります。
それを求めるにはL0ノルムを用いた最適化問題を解く必要があります。
L0ノルムは非ゼロ要素の個数を数えたものです。
しかし、ある式を満たすL0ノルムが最小となるような解は総当りで見つける必要があり、計算量が膨大になります。
そこで、L0ノルムの代わりにL1ノルムで近似できないかと考えられたようです。
L1ノルムは重みの絶対値の総和です。非ゼロ要素の数が少なく(つまり、重みがゼロの要素の数が多く)、重みが小さい値であるほど、ノルムの値が小さくなります。
確かにL0ノルムの最小化とL1ノルムの最小化は似ているように思います。
数式の解釈
続いて、Lassoの数式の解説に挑戦します。
自分は数学の専門家ではないため、以下の解説は厳密な定義やその証明や導出と異なる場合があります。
この記事ではLassoの回帰式は以下とします。
$$ L=\dfrac {1}{2n}\left|| y-Xw\right|| ^{2}+\lambda \left|| w\right|| _{1} $$
Lassoのアルゴリズムは複数ありますが、この記事では座標降下法(coordinate descent)について解説していきます。
座標降下法は、重みを1つずつ更新する操作を繰り返して行き、最適解に近似させる方法です。
複数の重みw0,w1,w2,...wkがあるとすると、一度に全ての重みを更新するのではなく、重みを、1つずつ順番に更新します。
注意点として、正則化項のL1ノルムは絶対値を含んでいるため、単純な微分ができません。
そのため、正則化項については左偏微分、右偏微分と場合分けをして重みを更新させる必要があります。
以降の説明では、流れをイメージし易くするために、回帰式に登場する変数を以下の通りと仮定します。
y = \begin{pmatrix}
y_{1} \\
y_{2} \\
y_{3}
\end{pmatrix}
、X = \begin{pmatrix}
1 & x_{11} & x_{12} & x_{13} \\
1 & x_{21} & x_{22} & x_{23} \\
1 & x_{31} & x_{32} & x_{33}
\end{pmatrix}
w = \begin{pmatrix}
w_{0} \\
w_{1} \\
w_{2} \\
w_{3}
\end{pmatrix}
yは目的変数の実測値、Xは説明変数とその値、wは重みを表しています。
Xの1列目の1は、w0(バイアス)に対応させるために挿入した列です。
この1列が入ることにより、Xとwの掛け算を
$$ Xw $$
と、バイアスを含めた形で簡素に表現できるようになります。
$$ \dfrac {1}{2n} $$
のnはサンプルサイズです。
この場合、Xが3行なので、3です。
このnがどこから登場してくる値なのか、その定義は理解できていないのですが、
このnがないと重みを0にし辛いというのは後々理解できました。
1/2は偏微分したときに都合が良いためであり、特に深い意味はないと考えます。
まず、w0の更新を考えます。
w0は正則化項に含まれませんので、正則化項を考慮する必要がありません。
ですので、
$$ L=\dfrac {1}{2n}\left|| y-Xw\right|| ^{2} $$
の部分だけに着目します。
この式を偏微分した式は、式変形は省略しますが、
$$ \dfrac {\partial L}{\partial w}=X^{T}Xw-X^{T}y $$
となります。
行列は分配法則が使えるので、これを
$$ X^{T}\left( Xw-y\right) $$
と変形し値を代入してみると、
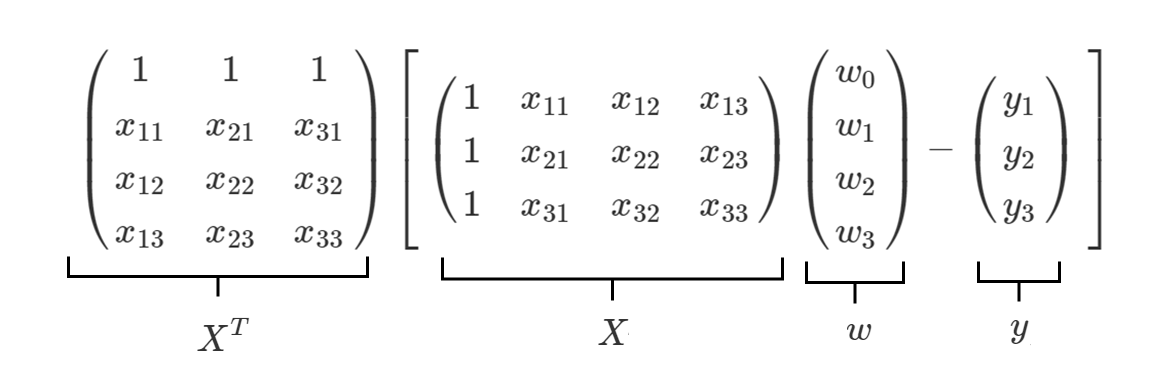
このようになります。
ここからさらに、下式の赤枠部分を変形し、
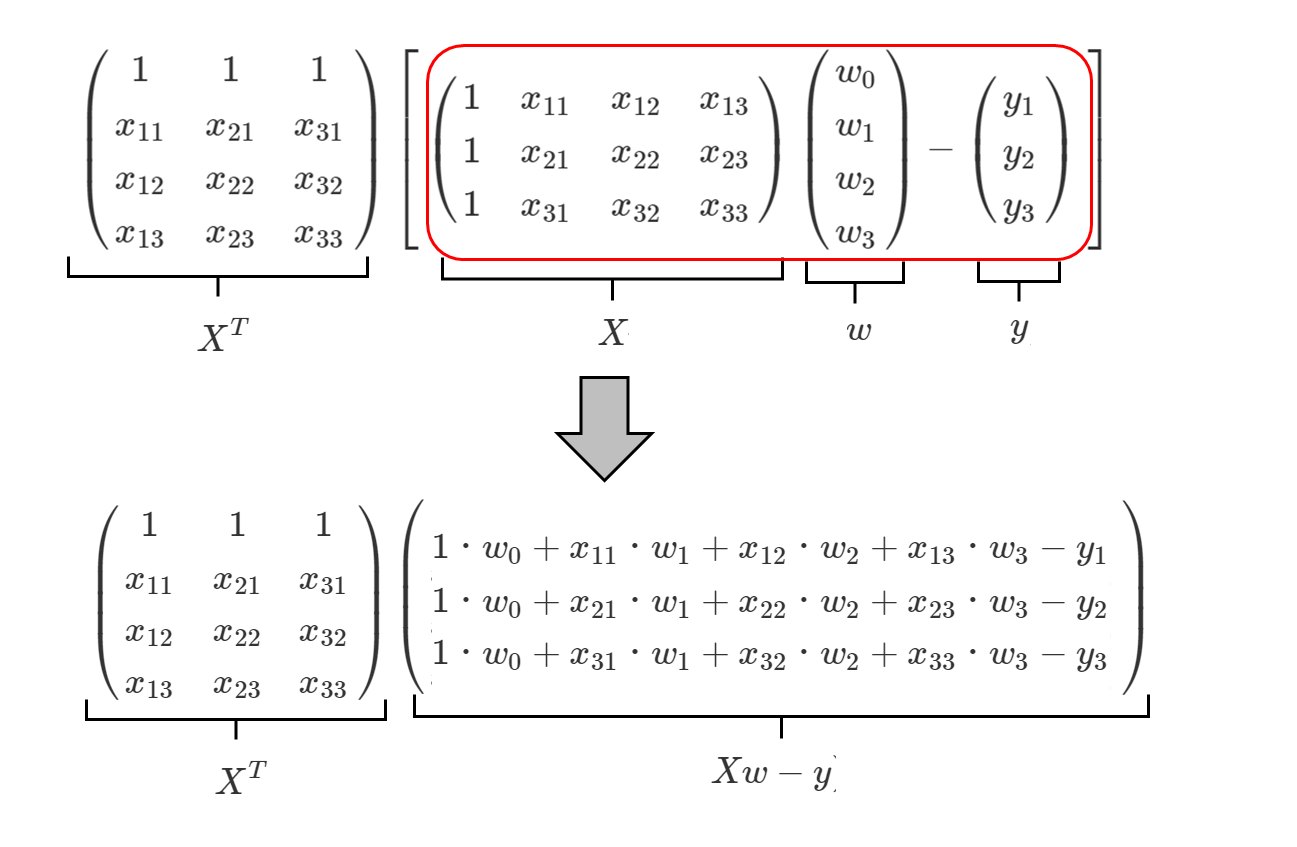
このようにします。
回帰式を偏微分した式は、下式のベクトルに対応すると考えます。
\dfrac {\partial L}{\partial w}
=
\begin{pmatrix}
\dfrac {\partial L}{\partial w_{0}} \\
\dfrac {\partial L}{\partial w_{1}} \\
\dfrac {\partial L}{\partial w_{2}} \\
\dfrac {\partial L}{\partial w_{3}} \\
\end{pmatrix}
ですので、w0は、下式の赤矢印の積が対応すると考えられ、
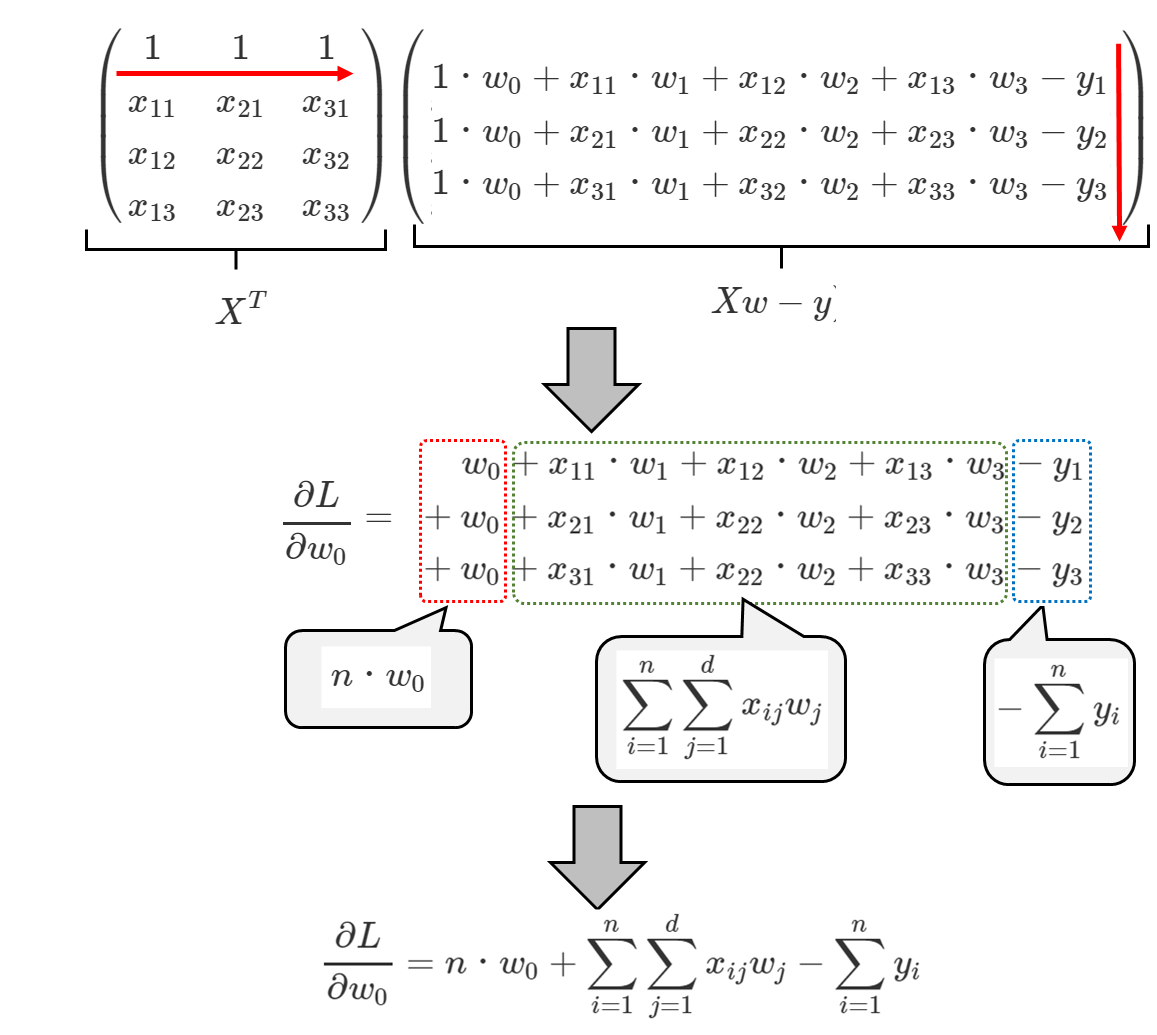
と求められます。
なお、iは行、jは列、dは次元数(列数)に対応しています。
この式が0となるようなw0を求めたいので、w0の更新式は、
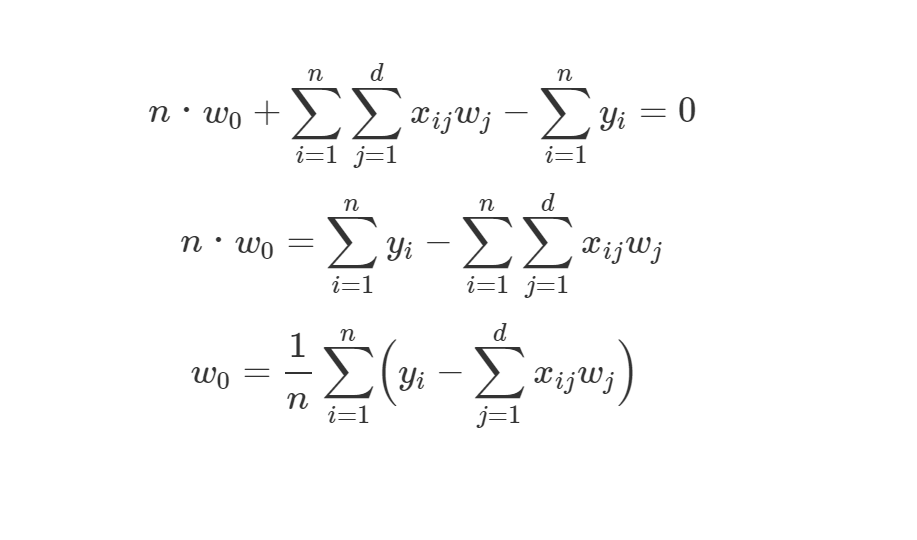
となります。
続いて、w1,w2,w3の更新式について考えていきます。
重みの更新式は
$$ \dfrac {\partial L}{\partial w_{k}}=X^{T}Xw-X^{T}y + n・λ$$
と仮定します。
n・λは正則化項を微分した値です。
正則化項に絶対値を含むので、後程、場合分けによって符号を変えていきます。
また、λの前にnを掛けるのは、元の回帰式の1/2nから来ています。
1/2は微分した際に消せますが、nは残るため、正則化項の微分した値に掛ける必要があります。
少し分かり難いかもしれませんので、以下の式をイメージして下さい。
$$ y = \dfrac{1}{2n}x^{2} + λ・x $$
この式を微分して=0としたいとすると、
$$ \dfrac{1}{n}x + λ = 0 $$
となり、
$$ x + n・λ = 0 $$
と変形できます。
それと同じことをこの式でもやりたいということです。
これらの更新式は、着目する重みが変わるだけで式の意味は同じです。
ですので、ここからはw1を例にみていきます。
右偏微分、左偏微分についてそれぞれ式変形をしていきます。
w1の右偏微分は、下式の青矢印の積にn × λを足したものと考えられ、
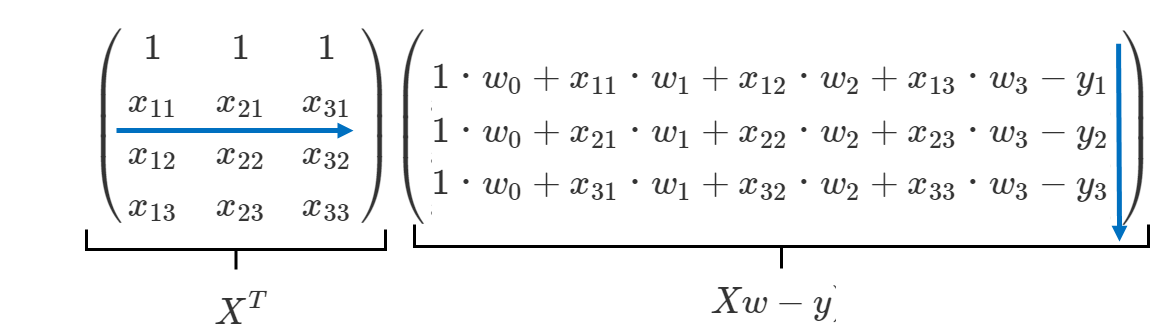
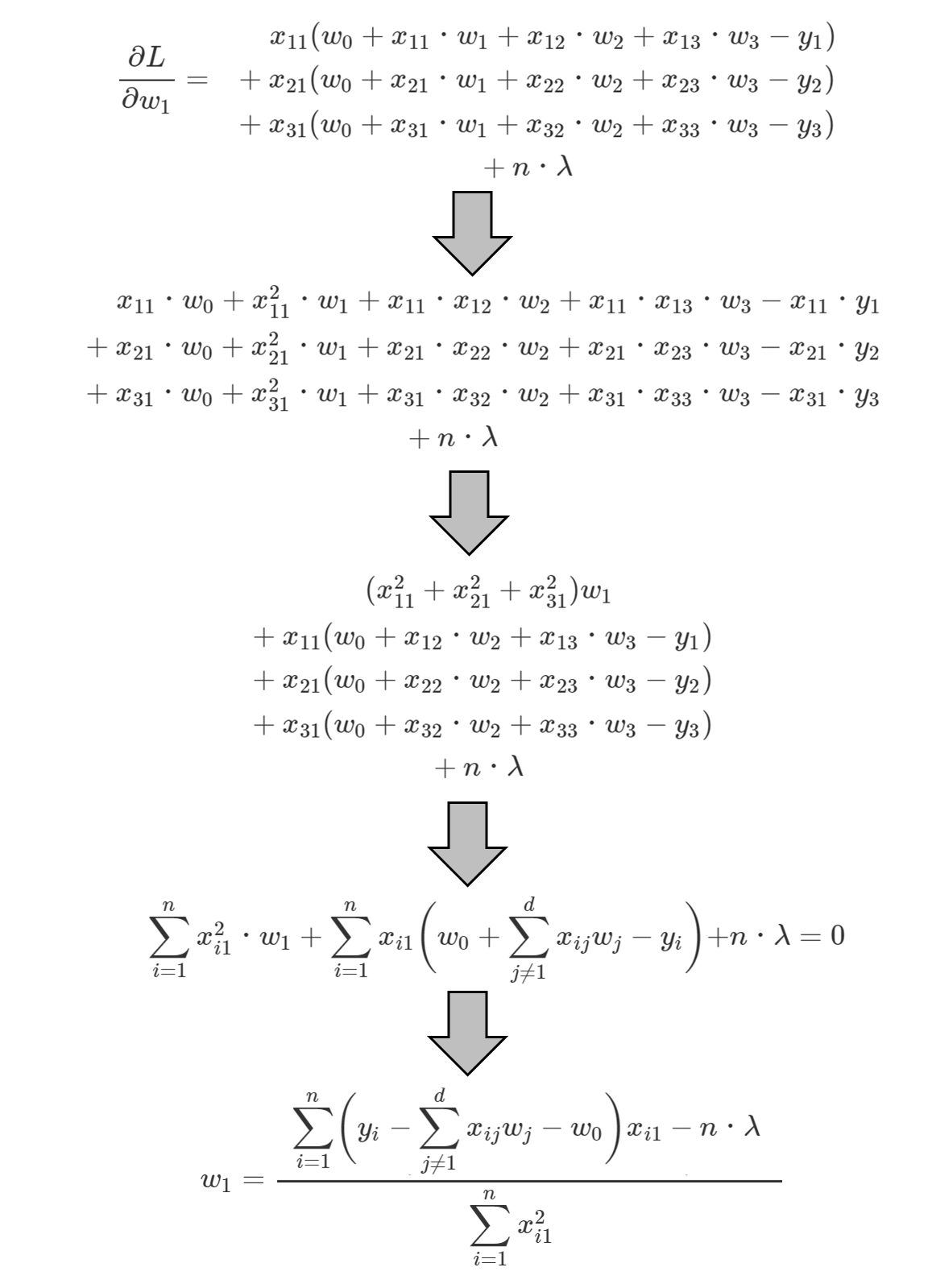
と変形できます。
w2、w3についても同様であるため、上式のw1をwkに置き換えます。
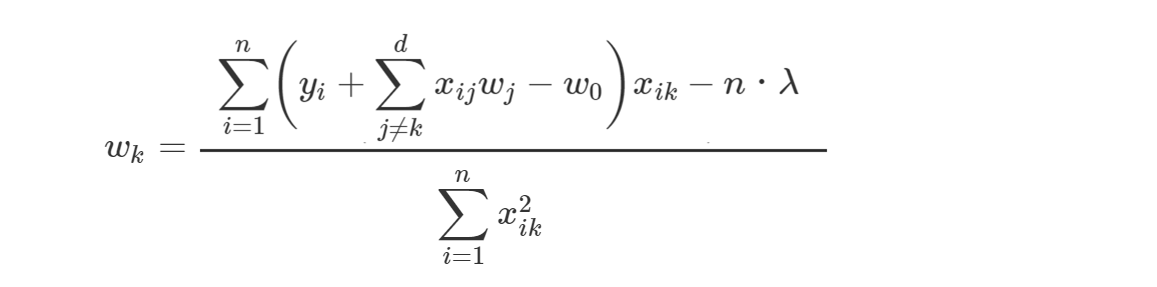
更に、wkの右偏微分の更新式であることを表すために、
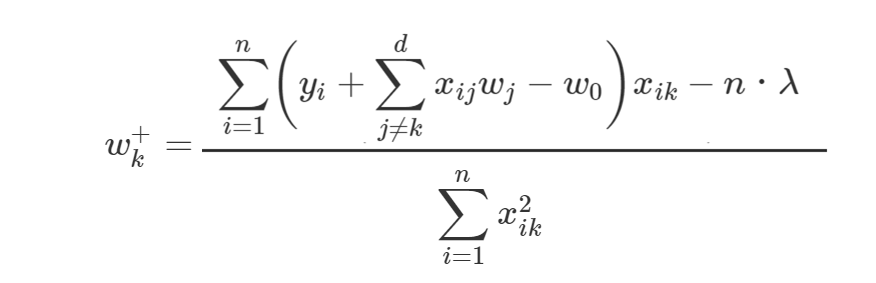
とします。
また、左偏微分は正則化項部分のn・λの符号を反転させ、
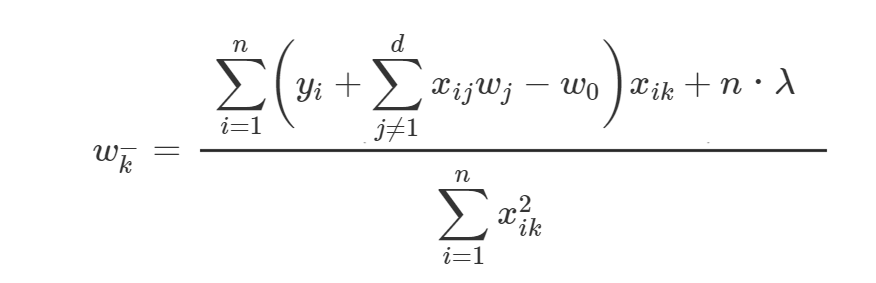
とします。
続いて、絶対値の場合分けについて考えていきます。
wkが正、つまり、
w_{k}^{+} > 0
となるのは、
\sum_{i=1}^{n}\biggl(y_{i} +
\sum_{j≠k}^{d}x_{ij}w_{j} - w_{0}\biggl)x_{ik} - n・λ > 0 \\
\sum_{i=1}^{n}\biggl(y_{i} +
\sum_{j≠k}^{d}x_{ij}w_{j} - w_{0}\biggl)x_{ik} > n・λ
の場合です。
wkが負、つまり、
w_{k}^{-} < 0
となるのは、
\sum_{i=1}^{n}\biggl(y_{i} +
\sum_{j≠k}^{d}x_{ij}w_{j} - w_{0}\biggl)x_{ik} + n ・λ < 0 \\
\sum_{i=1}^{n}\biggl(y_{i} +
\sum_{j≠k}^{d}x_{ij}w_{j} - w_{0}\biggl)x_{ik} < - n ・λ \\
の場合です。
それ以外の範囲、つまり、
- n ・ λ ≦ \sum_{i=1}^{n}\biggl(y_{i} +
\sum_{j≠k}^{d}x_{ij}w_{j} - w_{0}\biggl)x_{ik} ≦ n・λ
の場合、wkは0になります。
つまり、この範囲に該当する場合、wkの重みは0になるということです。
Lassoでパラメータの多くが0になるというのは、wkの更新式が上記の範囲に留まることが多いためと考えます。
(Lassoの目的としては寧ろパラメータの多くをここに留めたい)
λの値を大きくすれば、上記の範囲が拡がることが理解できます。
また、回帰式に含まれている
$$ \dfrac{1}{2n} $$
のnも、上記の範囲を拡げる意図があるのだと思います。
更新式の解説は以上です。
後はこれを収束条件を満たすまで、または、指定回数分重みを更新するなどして、最適解に近似させます。
機械学習のエッセンスでは、L1ノルムを次元数(列数)で割った値の変化量を収束条件の一つとして紹介されていました。
Pythonによるスクラッチ実装
収束条件は設けず、重み更新を1000回数繰り返すだけのプログラムです。
テストデータは、The Boston Housing Datasetを使用しました。
import pandas as pd
import numpy as np
# Bostonデータセットを読み込み
from sklearn.datasets import load_boston
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names).assign(MEDV=boston.target)
# 目的変数を抽出 ※ 目的変数は標準化前に抽出している点に注意
y = df.iloc[:,-1]
# データの標準化
df = (df - df.mean())/df.std()
# 説明変数を抽出
X = df.iloc[:,:-1]
# Xにバイアス(w0)用の値が1のダミー列を追加
X = np.column_stack((np.ones(len(X)),X))
n = X.shape[0] # 行数
d = X.shape[1] # 次元数(列数)
w = np.zeros(d) # 重み
r = 1.0 # ハイパーパラメータ ※ 正則化の強弱を調整する
for _ in range(1000) : # 以下の重み更新を1000回繰り返し
for k in range(d) : # 重みの数だけ繰り返し(w0含む)
if k == 0 :
# バイアスの重みを更新
w[0] = (y - np.dot(X[:,1:],w[1:])).sum() / n
else :
# バイアス、更新対象の重み 以外の添え字
_k = [i for i in range(d) if i not in [0,k]]
# wk更新式の分子部分
a = np.dot((y - np.dot(X[:,_k], w[_k]) - w[0]),X[:,k]).sum()
# wk更新式の分母部分
b = (X[:,k] ** 2).sum()
if a > n * r : # wkが正となるケース
w[k] = (a - n * r) / b
elif a < -r * n : # wkが負となるケース
w[k] = (a + n * r) / b
else : # それ以外のケース
w[k] = 0
print('----------- MyLasso1 ------------')
print(w[0]) # バイアス
print(w[1:]) # 重み
import sklearn.linear_model as lm
lasso = lm.Lasso(alpha=1.0, max_iter=1000, tol=0.0)
# MyLasso用に1列目にバイアスを追加しているため、それを除いてfitさせる
lasso.fit(X[:,1:], y)
print("---------- sklearn Lasso ------------")
print(lasso.intercept_)
print(lasso.coef_)
----------- MyLasso1 ------------
22.532806324110688
[ 0. 0. 0. 0. 0. 2.71517992
0. 0. 0. 0. -1.34423287 0.18020715
-3.54700664]
---------- sklearn Lasso ------------
22.53280632411069
[-0. 0. -0. 0. -0. 2.71517992
-0. -0. -0. -0. -1.34423287 0.18020715
-3.54700664]
やっていることは同じですが、もう少し簡素化して
import pandas as pd
import numpy as np
from sklearn.datasets import load_boston
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names).assign(MEDV=boston.target)
y = df.iloc[:,-1]
df = (df - df.mean())/df.std()
X = df.iloc[:,:-1]
X = np.column_stack((np.ones(len(X)),X))
n = X.shape[0]
d = X.shape[1]
w = np.zeros(d)
r = 1.0
for _ in range(1000) :
w[0] = (y - np.dot(X[:,1:],w[1:])).sum() / n
for k in range(1,d) :
w[k] = 0
a = np.dot((y - np.dot(X, w)),X[:,k]).sum()
b = (X[:,k] ** 2).sum()
w[k] = (np.sign(a) * np.maximum(abs(a) - n * r,0)) / b
print(w[0])
print(w[1:])
22.532806324110688
[-0. 0. -0. 0. -0. 2.71517992
-0. -0. -0. -0. -1.34423287 0.18020715
-3.54700664]
コードは以下でも公開しています。
https://github.com/torahirod/MyLasso
感想
Lassoを使うとなぜパラメータが0になるのか、その流れを理解できたかなと思います。
絶対値の微分の計算は、正直考え方が合っているのか不安です。
ですが、スクラッチ実装の実行結果がscikit-learnのLassoモデルの実行結果と一致したので、多分合っているのだと思います。
おわり