こんにちは。秋田県のIT企業、北日本コンピューターサービスのR&Dチーム「AUL(アウル)」に所属しています。トラフクロウです。
前回の記事ではセルフアテンションの計算を直感的に理解することを目標に、ベクトルをつかったイメージを紹介しました。今回はセルフアテンションを直感的にイメージするためのダメ押しの第二弾です。
前回はセルフアテンションの具体的な計算の仕方に注目していました。一方で今回は計算結果に注目して、すこし広い視点からセルフアテンションを考えてみたいと思います。
記事の中でつかう数式やイメージは、第1回目の内容を流用します。1回目の内容に興味のある方はこちらの記事をご参照ください。
この記事では多角形をつかってセルフアテンションを眺めます。
前半では、前回に引き続きトランスフォーマーの中でつかわれている各種セルフアテンションの計算方法を解説します。後半では、セルフアテンションの計算を、図形の変化に置き換えてとらえ直します。
以下、今回のお品書きです。
・トランスフォーマでつかわれる各種アテンションの計算方法の解説
・セルフアテンションは多角形の収縮で表現できる
トランスフォーマーは3種類のセルフアテンションをつかっている
トランスフォーマーが紹介された論文Attention Is All You Needでは、3種類のセルフアテンションが登場します。基本的な考え方はセルフアテンションと同じですが、それぞれビミョーな違いがあります。
ベクトルを細かく分割するマルチヘッドアテンション
まず1つ目はマルチヘッドアテンションです。マルチヘッドアテンションはトランスフォーマーの文脈解析能力を強化する目的で採用されています(詳しくはこちら)。
マルチヘッドアテンションの計算では、ベクトルを ヘッド とよばれる細かい単位に分割します。例えば、 $8$ 次元ベクトルがあったとして、これを4つのヘッドに分けると次のようになります。
\begin{pmatrix}
2 \\
1 \\
1 \\
7 \\
1 \\
3 \\
6 \\
1
\end{pmatrix}
\Longrightarrow
\begin{pmatrix}
2 \\
1
\end{pmatrix},
\begin{pmatrix}
1 \\
7
\end{pmatrix},
\begin{pmatrix}
1 \\
3
\end{pmatrix},
\begin{pmatrix}
6 \\
1
\end{pmatrix}
実際の処理ではキー、クエリ、バリューベクトルを作るときにベクトルの分割が行われます。前回の解説では $D$ 次元の単語ベクトルに $(D, D)$-型の行列 $W_K, W_Q, W_V$ を掛け算して3種類のベクトルを作りました。
対して、マルチヘッドアテンションでは $(\frac{D}{H}, D)$-型の行列をつかいます。ここで $H$ はヘッドの数で、かならず $D$ を割り切ることができる数に設定します。また、用意する行列はキー、クエリ、バリューごとに $H$ 個ずつです。つまりヘッドを4つ用意しようと思ったら
\begin{align*}
& W_K^{(1)}, W_K^{(2)}, W_K^{(3)}, W_K^{(4)} \\
& W_Q^{(1)}, W_Q^{(2)}, W_Q^{(3)}, W_Q^{(4)} \\
& W_V^{(1)}, W_V^{(2)}, W_V^{(3)}, W_V^{(4)} \quad \quad (ただし W_*^{{(i)}} は(D/4, D)型の行列)
\end{align*}
だけの行列を準備する必要があります。
ここで、単語ベクトル $\boldsymbol{x_j}$ に各 $W_*^{{(i)}}$ を掛け算した結果を
\begin{align*}
\boldsymbol{k}_j^{(i)} &= W_K^{{(i)}} \boldsymbol{x}_j \\
\boldsymbol{q}_j^{(i)} &= W_Q^{{(i)}} \boldsymbol{x}_j \\
\boldsymbol{v}_j^{(i)} &= W_V^{{(i)}} \boldsymbol{x}_j \quad \quad (i = 1, 2, 3, 4)
\end{align*}
と書くことにします。行列積の性質から $\boldsymbol{k}_j^{(i)}, \boldsymbol{q}_j^{(i)}, \boldsymbol{v}_j^{(i)}$ は $\frac{D}{4}$ 次元ベクトルです。
これらのベクトルをつかって各 $i$ 番目のヘッドごとにセルフアテンションを計算していきます。$i$ 番目のヘッドに関するキー、クエリ、バリュー行列を
K^{(i)}, Q^{(i)}, V^{(i)}
と書くことにしましょう。このときのアテンションベクトルは、前回見たように、次の式で計算されます。
A^{(i)} = V^{(i)} \cdot \text{softmax} \Biggl( \displaystyle{\frac{K^{(i)T} Q^{(i)}}{\sqrt{D/4}}} \Biggr) \quad \quad ( 4はヘッドの数、実際はH )
$A^{(i)}$ の $j$ 列目には $j$ 番目の入力単語にあたるベクトル(の一部)が入っています。これを $\boldsymbol{a}_j^{(i)}$ と書きましょう。すべてのヘッドの計算が完了したら、各ヘッドを再度連結し元の大きさのベクトル $\boldsymbol{a}_j$ に復元します。すなわち
\boldsymbol{a}_j =
\begin{pmatrix}
\boldsymbol{a}_j^{(1)} \\ \\
\boldsymbol{a}_j^{(2)} \\ \\
\boldsymbol{a}_j^{(3)} \\ \\
\boldsymbol{a}_j^{(4)}
\end{pmatrix} \quad \quad (\boldsymbol{a}_jはD次元ベクトル)
です。以上がマルチヘッドアテンションの計算です。
式からもわかりますが、各ヘッドではそれぞれ個別の行列($W_K^{(i)}, W_Q^{(i)}, W_V^{(i)}$)をつかってアテンションベクトル $\boldsymbol{a}_j^{(i)}$ を計算します。これはヘッドごとに異なる視点でベクトルを表現しているということです。実際に元の論文では、各ヘッドごとに異なるアテンションが計算されることがわかったと記されています。

Attention Is All You Need より引用(Figure5)
マルチヘッドアテンションによる多角的な文脈解析がトランスフォーマーの高い文章読解力を実現しているのではないかということが、現在の通説になっているそうです。
いくつかの単語を隠すマスクマルチヘッドアテンション
マスクマルチヘッドアテンションはトランスフォーマーのデコーダーで採用されているマルチヘッドアテンションです。トランスフォーマーのAI学習を行う際に重要な役割を果たします。
トランスフォーマーが日本語を英語に翻訳するために訓練をしている場面を考えてみましょう。すなわち、トランスフォーマーに「これはペンです」を入力すると「This is a pen」を出力できるようになってほしいという状況です。

トランスフォーマーの訓練は入力文と、その模範解答となる出力を与えることで行われます。このとき、模範解答の文章は1単語ずつ マスクトークン とよばれる記号で隠された状態でわたされます。トランスフォーマーは訓練の中で各マスクトークンにどんな単語を入れるべきか予測し、答え合わせを行います。答え合わせの結果によって予測方法を微修正することで、しだいに正しい翻訳が行えるようになるのです。
このように単語を隠す(マスクする)ことがマスクマルチヘッドアテンションの名前の由来となっています。

マスクトークンをつかう理由は $i$ 番目の単語を予測するときに、トランスフォーマーがカンニングできないようにするためです。
第1回目で見たようにセルフアテンションは行列の掛け算のみで計算することができます。これにより、複数の単語に関する計算を1回で終えることができ、非常に高い計算効率を実現しています(トランスフォーマーが売りにしているポイントです)。
しかしこの並列計算が単語予測の場面では問題となってしまいます。というのも、すべての単語を並列で処理する都合上、まだ出力していない単語までも計算に考慮してしまうのです。
これでは、模範解答がないと答えを言うことができないAIモデルになってしまいます。しかし、実際の場面で翻訳機として働くためには、あらゆる文章に、模範回答なしで、臨機応変に対応する必要があります。
そこで心を鬼にして、トランスフォーマーがまだ予測していない単語を、すべてマスクトークンで見えなくしてあげます。つまり「This is」まで翻訳した場合は、「This is」の情報のみで次の「a」を予想できるように訓練してあげるのです。
ここまでくれば、あとは上で紹介したマルチヘッドアテンションの計算を適用するだけです。ただし、マスクトークンに対応するベクトルのあつかいが少々異なります。次の式は $i$ 番目の単語を予想する場合の計算式です。
c_{ij}^{(h)} =
\begin{cases}
\displaystyle{\frac{\boldsymbol{k}_i^{(h)} \cdot \boldsymbol{q}_j^{(h)}}{\sqrt{D/H}}} \quad (j \leq i, \ hはヘッドの番号) \\
- \infty \quad (i < j)
\end{cases}
このようにマスクされた単語に関するアテンションが $-\infty$ になっています。これは、このあとで各アテンション $\boldsymbol{c}_i^{(h)}$ をソフトマックス関数に入力することを考えての都合です。
ソフトマックス関数は、指数関数で変換した値について全体の割合を求める関数でした。そのため、
e^{-\infty} = 0
として考えると、マスクされた単語ベクトルを無視してアテンションベクトルを作ることができるのです。

エンコーダーとデコーダーをつなぐクロスアテンション
クロスアテンションの役割は、エンコーダーから受けとったベクトルと、マスクマルチヘッドアテンションが計算したベクトルをミックスすることです。これにより、翻訳する文章の情報と、これまで翻訳した内容を同時に考えて処理することができるようになります。

クロスアテンションの計算もマルチヘッドアテンションと同じ式をつかいます。ただし、マスクマルチヘッドアテンションを通過したベクトルからクエリベクトルを計算し、エンコーダーの出力ベクトルからキー、バリューベクトルを計算して、アテンションベクトルを求めていきます。
計算式の構成は次のとおりです。
A^{(i)}_{cross} = V^{(i)}_{encoder} \cdot \text{softmax} \Biggl( \displaystyle{\frac{K^{(i)T}_{encoder} Q^{(i)}_{mask-multihead}}{\sqrt{D/H}}} \Biggr)
セルフアテンションを多角形で考えてみた
ここまでは、トランスフォーマーの中でつかわれているセルフアテンションの計算方法を追いかけてきました。ここからは、もう少しグローバルな視点でセルフアテンションを眺めてみたいと思います。
第1回目の冒頭で書いたように、セルフアテンションの計算は多角形の収縮として解釈することができます。

トランスフォーマーと多角形の間に特別な関係などないように感じるかもしれませんが、順を追って見ていきましょう。
多角形を見つける準備
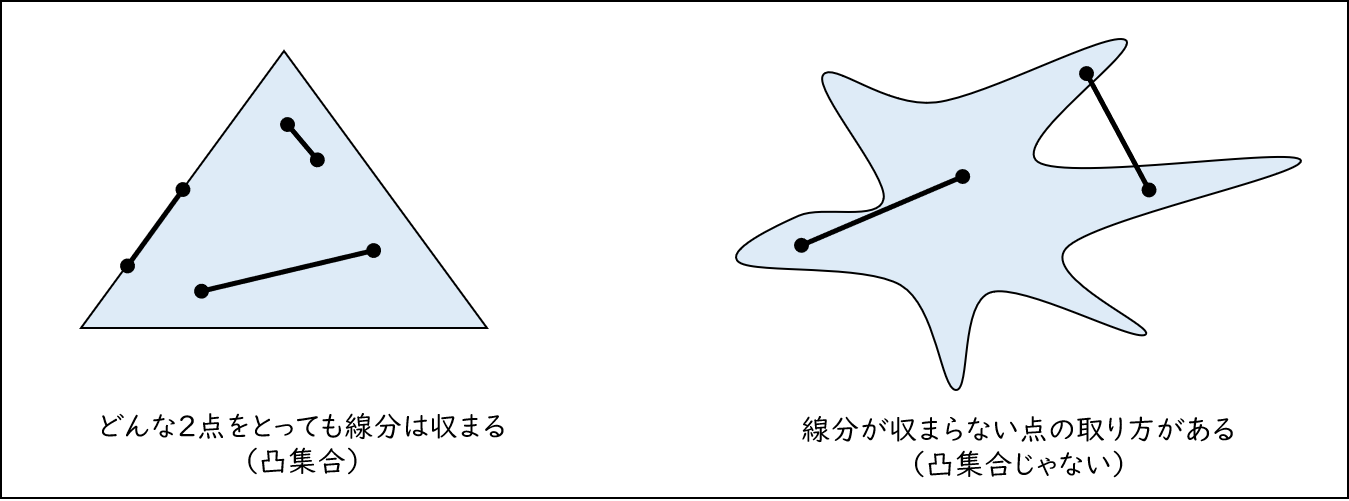
トランスフォーマーにひそむ多角形を見つけることができるように、数学の道具を2つ用意します。凸集合(とつしゅうごう) と 凸包(とつほう) です。
数学では図形を空間上の点を集めて作った点の集合体として扱います。三角形のようにキレイな集め方をすることもできますが、アメーバのように適当に点を集めることもできます。

このとき、ある程度キレイな図形のみを考えるためのルールを考えます。逆にいうと、アメーバのようにボコボコへこんでいる図形は除外するようにしたいのです。そこで、ボコボコへこんでいない図形のことを凸集合とよぶ ことにします。
へこんでいる、いないを厳密に表現するために点の集まり $A$ が凸集合であるためのルールを次のように定めましょう。
これで、ボコボコしていない図形のみを考えることができますね。
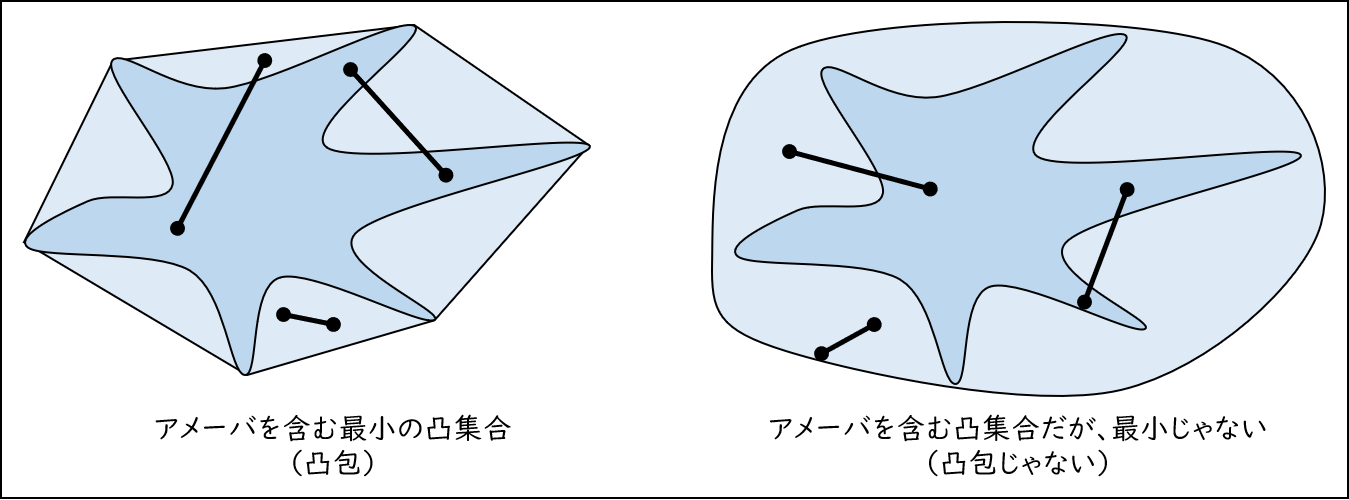
しかし、キレイじゃない認定をされてしまったアメーバ型の図形は少しかわいそうな気もします。そこで、彼らを救済するためにキレイな図形になるチャンスを与えましょう(やっぱり仲間外れはよくないよね)。
具体的には、ボコボコしている隙間をうまいこと埋めてあげる措置をほどこします。このようにして隙間を埋められた図形を凸包 とよび、次のルールで定めます。
「A を含む凸集合はいつでも存在するの?」、「凸集合の最小ってなに?」という細かい部分の補足です(気にならなければスキップでOKです)。
【$A$ を含む凸集合はいつでも存在するの?】
$A$ を含む集合 $B$ が凸集合でないとします。このとき $B$ を凸集合でなくしている線分(はみ出し者)をすべて集めてきて、まるっと $B$ に加えてあげます。その加えた結果を $B^{\prime}$ とすれば $B^{\prime}$ は凸集合です。

【凸集合の最小ってなに?】
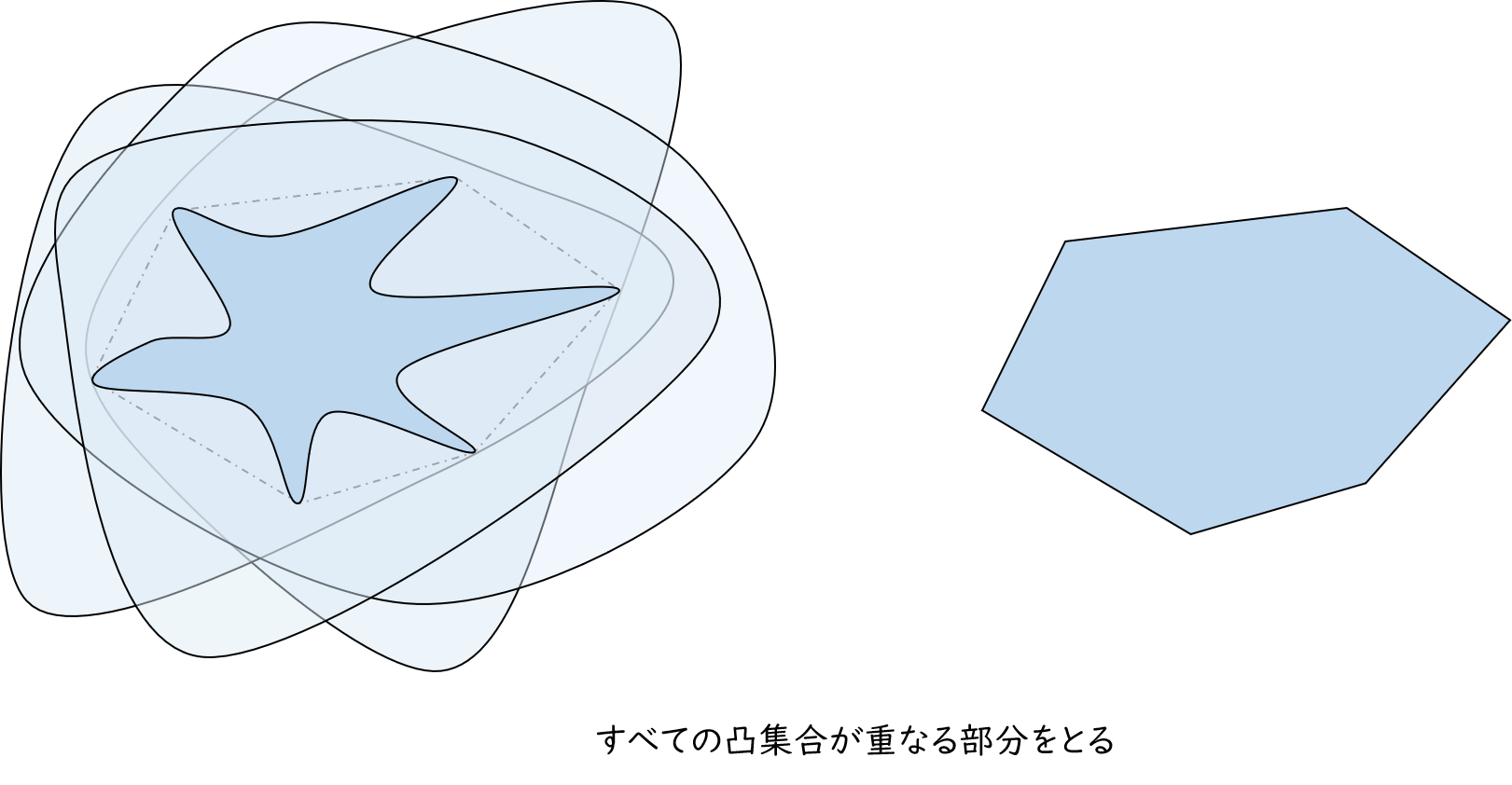
集合 $A$ を含む凸集合は無数にあります。たとえば、$A$ を含む凸集合 $B$ 、をさらに含む凸集合 $C$ ・・・のように無限に議論できることからもイメージしやすいかと思います。
そこで、無限個の凸集合をすべて重ね合わせて、全部の凸集合に共通で含まれている部分を切り出してみます。すると切り出された部分は、もとの集合 $A$ を含みつつ、どんな凸集合よりも小さい凸集合になります。
トランスフォーマーに入力される文章は多角形になっていた
上で見た凸包をトランスフォーマーの入力に適用してみましょう。トランスフォーマーに入力された文章は単語分割され、その後ベクトル化されます。
ベクトルには空間内の点としての側面がありました。そのため、各単語ベクトルを集めたものは有限個の点を集めた集合と考えることができます。
下の図は単語ベクトルを点として見た場合のイメージです。青色の点1つ1つが単語です(イメージのしやすさを優先して $2$ 次元にしています)。

この単語の点集合にも当然凸包を考えることができます。上の点たちの凸包は下のように多角形の領域になります。

以上のことから、1つの文章に対し何かしらの多角形が存在する ことがわかりました。
トランスフォーマーの単語ベクトルの作り方を考えると、1つの文章に対して1つの多角形が唯一決まります。そのため、トランスフォーマー上で文章を考える場合は、それを多角形に置き換えても等価の議論を行うことができます。
セルフアテンションとは多角形を収縮させる操作だった
文章と多角形が等価なものであるなら、文章についてのセルフアテンションの計算を多角形で再現できるはずです。それではセルフアテンションを適用した後の多角形はどうなるのでしょうか?
セルフアテンションを適用した多角形を考えるために凸包に関する次の性質を紹介します。
凸包内部の点の性質
いくつかの点 $\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots , \boldsymbol{x}_m$ の集合 $A$ があり、その凸包を $Conv(A)$ とする。
このとき、$Conv(A)$ の内部の点 $\boldsymbol{x}$ は
\boldsymbol{x} = \lambda_1 \boldsymbol{x}_1 + \lambda_2 \boldsymbol{x}_2 + \cdots + \lambda_m \boldsymbol{x}_m \quad (ただし、\lambda_1 + \lambda_2 + \cdots + \lambda_m = 1, \lambda_i \geq 0)
と書くことができる。

初見では非自明な主張だと思うので、証明を載せておきます(長いのでスキップでもOKです)。
$A$ の点 $\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots , \boldsymbol{x}_m$ をつかって計算される点
\boldsymbol{x} = \lambda_1 \boldsymbol{x}_1 + \lambda_2 \boldsymbol{x}_2 \cdots + \lambda_m \boldsymbol{x}_m \quad \quad (ただし、\lambda_1 + \lambda_2 + \cdots + \lambda_m = 1, \lambda_i \geq 0)
をすべて集めた集合を $\sigma_A$ と書くことにします。このとき $\sigma_A$ が $A$ の凸包の条件を満たすことを示します。
$\sigma_A$ が $A$ の凸包であることを示すには、凸包の定義より、次の2つが成り立てばいいです。
- $\sigma_A$ は $A$ を含む凸集合である
- $\sigma_A$ は $A$ を含む凸集合の中で最も小さい集合である
1つ目の条件について ですが、$\sigma_A$ が $A$ を含むことは明らかです。$i$ 番目の点 $\boldsymbol{x}_i$ について $\lambda_i = 1$、それ以外の $\lambda_j$ を $0$ にすれば、$\boldsymbol{x} = \boldsymbol{x}_i$ となるためです。
凸集合であることを示すために、$\sigma_A$ からどんな点でもいいので適当に2点 $\boldsymbol{a}, \boldsymbol{b}$ を取ります。この2つの点は $\sigma_A$ の点なので次のように書くことができます。
\begin{align*}
\boldsymbol{a} &= a_1 \boldsymbol{x}_1 + a_2 \boldsymbol{x}_2 + \cdots + a_m \boldsymbol{x}_m \quad \quad (a_1 + a_2 + \cdots + a_m = 1, a_i \geq 0) \\
\boldsymbol{b} &= b_1 \boldsymbol{x}_1 + b_2 \boldsymbol{x}_2 + \cdots + b_m \boldsymbol{x}_m \quad \quad (b_1 + b_2 + \cdots + b_m = 1, b_i \geq 0)
\end{align*}
ここで2点 $\boldsymbol{a}, \boldsymbol{b}$ を結んでできる線分上の点 $\boldsymbol{y}$ は次のように書けます。
\boldsymbol{y} = (1-t) \boldsymbol{a} + t \boldsymbol{b} \quad \quad ( 0 \leq t \leq 1)
数式だけだとわかりづらいですが、$t=0$ のとき $\boldsymbol{y} = \boldsymbol{a}$ であることと、$t$ をじわじわ $1$ に近づけていくと徐々に $\boldsymbol{y} = \boldsymbol{b}$ となることを考えると、線分上の点であることをイメージしやすいです。

この点 $\boldsymbol{y}$ の式を変形すると
\begin{align*}
\boldsymbol{y} &= (1-t) \boldsymbol{a} + t \boldsymbol{b} \\
&= (1-t)a_1 \boldsymbol{x}_1 + \cdots + (1-t)a_m \boldsymbol{x}_m + tb_1 \boldsymbol{x}_1 + \cdots + tb_m \boldsymbol{x}_m \\
&= (a_1 - ta_1 + tb_1) \boldsymbol{x}_1 + \cdots + (a_m - ta_m + tb_m) \boldsymbol{x}_m
\end{align*}
となります。ここで、$a_i$ と $b_i$ の総和はそれぞれ $1$ だったので、$\lambda_i = a_i - ta_i + tb_i$ とおくと
\begin{align*}
\lambda_1 + \lambda_2 + \cdots + \lambda_m &= (a_1 - ta_1 + tb_1) + (a_2 - ta_2 + tb_2) + \cdots (a_m - ta_m + tb_m) \\
&= (a_1 + \cdots + a_m) - t(a_1 + \cdots + a_m) + t(b_1 + \cdots + b_m) \\
&= 1 - t + t = 1
\end{align*}
となり、$\boldsymbol{y}$ は $\sigma_A$ 内の点であることがわかります。よって、$\sigma_A$ からどんな2点をとって線分を考えても、それは $\sigma_A$ に収まることがわかりました(条件1はクリア)。
次に $\sigma_A$ が $A$ を含む凸集合の中で最小であることを示します。 この証明は少し面倒です。$\sigma_A$ より小さい凸集合 $\sigma_A^{\prime}$ が存在すると仮定して矛盾を起こします(つまり、そんな $\sigma_A^{\prime}$ は存在しちゃいけないことを示します)。
$\sigma_A^{\prime}$ は $\sigma_A$ よりも小さいので $\sigma_A$ には含まれるが、$\sigma_A^{\prime}$ には含まれない点 $\boldsymbol{x}$ が存在します。

ここで、点集合 $A$ から $\boldsymbol{x}_1$ を取ってきます。そして、 $\boldsymbol{x}_1$ を始点にして $\boldsymbol{x}$ を通るような半直線を考えてみましょう。すると、$\boldsymbol{x}$ を通過した以降で現れる点 $\boldsymbol{x}^{\prime}$ はどれも $\sigma_A^{\prime}$ には含まれません。

なぜ $\boldsymbol{x}^{\prime}$ が $\sigma_A^{\prime}$ に含まれないのか、理由は以下の通りです。まず、$\sigma_A^{\prime}$ は $A$ を含むので、$\boldsymbol{x}_1$ を含んでいます。ここで、もしも $\sigma_A^{\prime}$ が $\boldsymbol{x}^{\prime}$ を含むのならば、凸集合の定義から、$\boldsymbol{x}_1$ と $\boldsymbol{x}^{\prime}$ 端点とする線分が $\sigma_A^{\prime}$ に収まることになります。
しかし、これでは $\boldsymbol{x}_1$ と $\boldsymbol{x}$ 端点とする線分も $\sigma_A^{\prime}$ 内に収まることになってしまい、$\sigma_A^{\prime}$ が $\boldsymbol{x}$ を含まないという仮定に違反してしまいます。そのため、$\boldsymbol{x}^{\prime}$ は $\sigma_A^{\prime}$ に含まれないのです。
さて、$\boldsymbol{x}_1$ を始点にして $\boldsymbol{x}$ を通るような半直線をずっと伸ばしていくと、それはいずれ $\sigma_A^{\prime}$ の境界部分(縁)にぶつかります。上の議論により、半直線と境界の交点 $\boldsymbol{x}^{\prime}$ は $\sigma_A^{\prime}$ に含まれてはいけません。

ここで、$\boldsymbol{x}^{\prime}$ は $\sigma_{A \setminus {x_1 }}$ の点になります($A \setminus {\boldsymbol{x}_1 }$ は集合 $A$ から $\boldsymbol{x}_1$ を抜いた集合の意味です)。
なぜかというと、まず、$\boldsymbol{x}_1$ を始点として $\boldsymbol{x}$ を通る半直線は次の式で書けます。ただし $t$ は $0$ 以上の値をとるパラメータです。
\boldsymbol{x}^{\prime} = \boldsymbol{x}_1 + t(\boldsymbol{x}-\boldsymbol{x}_1) \quad (t \geq 0)
$t=0$ のときに $\boldsymbol{x}_1$、$t=1$ のときに $\boldsymbol{x}$、$t > 1$ で適当な座標という変化を考えると半直線であることがイメージしやすいです。$\boldsymbol{x}$ が $\sigma_A$ の点であることを考えると
\begin{align*}
\boldsymbol{x}^{\prime} &= \boldsymbol{x}_1 + t(\boldsymbol{x}-\boldsymbol{x}_1) \\
&= \boldsymbol{x}_1 + t(\lambda_1 \boldsymbol{x}_1 + \lambda_2 \boldsymbol{x}_2 + \cdots + \lambda_m \boldsymbol{x}_m -\boldsymbol{x}_1) \\
&= \{1 + t(\lambda_1 - 1)\} \boldsymbol{x}_1 + t\lambda_2 \boldsymbol{x}_2 + \cdots + t\lambda_m \boldsymbol{x}_m
\end{align*}
と変形できます。ここで、$\boldsymbol{x}_1$ の影響がなくなるときの $t$、 つまりは $\boldsymbol{x}_1$ の係数が $0$ となる場合の $t$ を求めると
\begin{align*}
1 + t(\lambda_1 - 1) &= 0 \\
t(\lambda_1 - 1) &= -1 \\
t = \frac{1}{1 - \lambda_1}
\end{align*}
となります。ここでいう $\boldsymbol{x}_1$ の影響を受けない とは $\sigma_A$ 内で $\boldsymbol{x}_1$ から最も離れている領域を見ていることと同義です(つまりは $\boldsymbol{x}_1$ から最も遠い位置にある縁を見ている)。
そして $t = \frac{1}{1 - \lambda_1}$ のときの $\boldsymbol{x}^{\prime}$ は
\boldsymbol{x}^{\prime} = \frac{\lambda_2}{1 - \lambda_1} \boldsymbol{x}_2 + \frac{\lambda_3}{1 - \lambda_1} \boldsymbol{x}_2 + \cdots + \frac{\lambda_m}{1 - \lambda_1} \boldsymbol{x}_2
となりますが、
\begin{align*}
\lambda_1 + \lambda_2 + \cdots \lambda_m &= 1 \\
\lambda_2 + \cdots \lambda_m &= 1 - \lambda_1
\end{align*}
であることに注意すると、$\boldsymbol{x}^{\prime}$ は $\sigma_{A \setminus {x_1 }}$ の点であることがわかります。
この $\boldsymbol{x}^{\prime}$ と $\sigma_{A \setminus {\boldsymbol{x_1} }}$ について、これまでの議論を繰り返し適用することで、$\sigma_{A \setminus {\boldsymbol{x_1}, \boldsymbol{x_2}, \cdots , \boldsymbol{x_{m-1}} }}$ 内の点である $\boldsymbol{y}$ を得ることができます。$\boldsymbol{y}$ の作り方から、$\boldsymbol{y}$ は $\sigma_A^{\prime}$ に含まれてはいけません。
しかし、$\sigma_A$ の定義を思い出すと、
\sigma_{A \setminus \{\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots , \boldsymbol{x}_{m-1} \}} = \{\boldsymbol{x}_{m}\}
であることがわかるため、$\boldsymbol{y} = \boldsymbol{x}_{m}$ となってしまいます。これは $\sigma_A^{\prime}$ が 集合 $A$ の点をすべてふくむという仮定に矛盾します。したがって、$\sigma_A$ より小さい凸集合 $\sigma_A^{\prime}$ は存在せず、$\sigma_A$ 自身が最小の凸集合であることがわかりました(条件2クリア)。
したがって、$Conv(A) = \sigma_A$ が成り立ち、主張が示されました。
この主張を可視化したのが下の図です。青い点が集合 $A$ の点で、青い線で囲まれた領域が $A$ の凸包 $Conv(A)$ になります。そして緑の点が、主張の式で計算された $\boldsymbol{x}$ です。点の数を増やしていくと、たしかに凸包の内部に点が収まることが確認できます。

このような仰々しい主張を持ち出したのにはちゃんと理由があります。なんと、主張内の式が、セルフアテンションの計算結果と一致してしまう のです。セルフアテンションの計算はバリューベクトルに、ソフトマックス関数を通したアテンションを掛け算して、それらを足しあわせることで行われます。
\boldsymbol{a}_i = c_{i1}^{\prime} \boldsymbol{v}_1 + c_{i2}^{\prime} \boldsymbol{v}_2 + c_{i3}^{\prime} \boldsymbol{v}_3 + c_{i4}^{\prime} \boldsymbol{v}_4
そして、ソフトマックス関数とは入力値すべての総和を $1$ に変換する関数であり、しかもその値は必ずプラスの値をとる性質がありました。
つまり、セルフアテンションを計算して得られるベクトル(点)は、すべてのバリューベクトルの集合 $V$ の凸包 $Conv(V)$ に含まれる点になっているのです。

さらに、1つのバリューベクトルに対し、1つのアテンションベクトルが定まります。これまでの観察から、アテンションベクトルは凸包の内側に入ります。そのため、計算後のアテンションベクトルの集合 $A$ に対し、さらに凸包 $Conv(A)$ を考えると、多角形 $Conv(A)$ は 多角形 $Conv(V)$ に含まれてしまうのです。
したがって、セルフアテンションを計算するということは元の単語ベクトルが作る多角形を、さらに小さな多角形に縮める操作であると解釈できる のです。

収縮で多角形の辺の数は変化する
今回の観察から分かることは、セルフアテンションを適用することで多角形がさらに小さい多角形にうつるということだけです。
多角形の頂点の数や辺の数が変換の前後で変わる場合もあることに注意してください(五角形が変換後に三角形になることもある)。
マルチヘッドアテンションでは複数の多角形を同時に操作している
ここまでで、セルフアテンションが、多角形を収縮させていることがわかりました。しかし、トランスフォーマーで実際に採用されているのはマルチヘッドアテンションです。この場合はどう解釈すればよいのでしょうか?
僕の考えは、マルチヘッドアテンションの各ヘッドをパラレルワールドだと思うことにする です。
この記事の上で見たようにマルチヘッドとは高次元ベクトルを、等しい次元のサブベクトルに分割する戦略です。これは、大きな次元の空間を、独立した小さい次元の小部屋に分けていると考えることができます。
次は $3$ 次元の場合の例です。$3$ 次元空間は $x, y, z$ の3本の軸がるため、3つの独立した $1$ 次元の小部屋に分割できます。
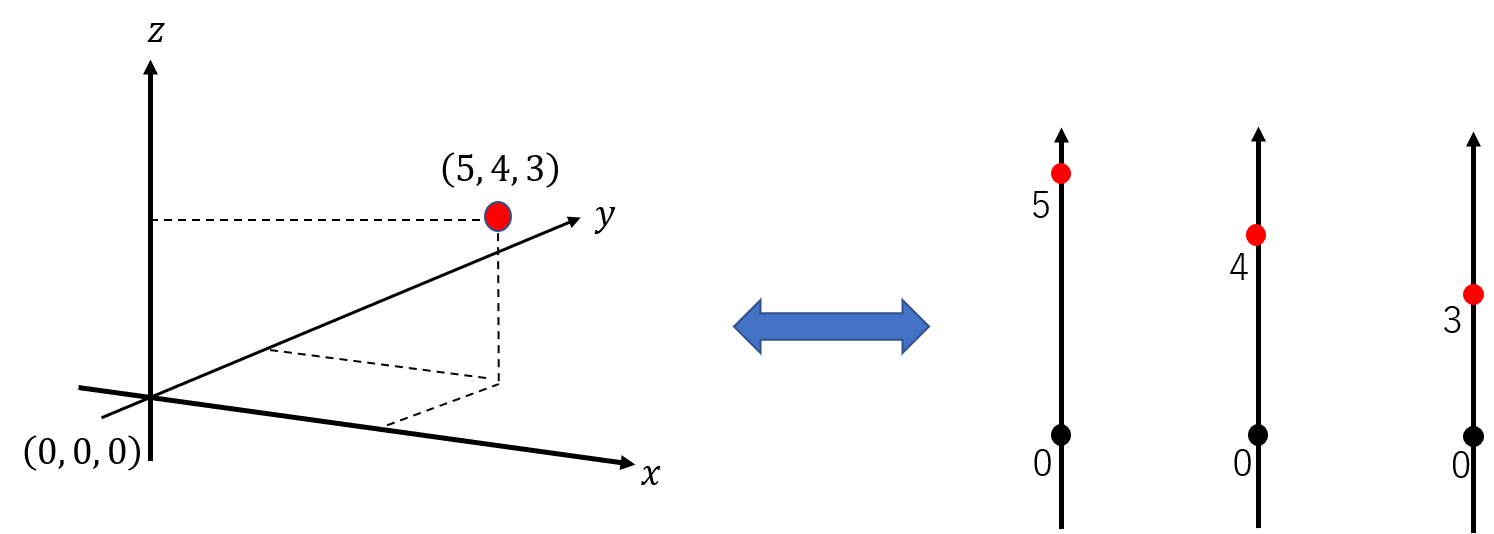
冒頭で紹介した $8$ 次元ベクトルを4つのヘッドに分ける操作は、4つの独立した $2$ 次元平面を同時に考えていることと同じです。

マルチヘッドアテンションでは、各ヘッドに対し個別にセルフアテンションを計算していました。そのため多角形をつかった解釈をすると、ヘッドの数だけ多角形が作られ、それらが互いの干渉を受けることなく個別に縮小される ということになります。つまり、ある文章を表現する多角形がパラレルワールドでまったく別の縮められ方をしているのです。
元の論文では各ヘッドで計算されるアテンションはまったく別物であるという結果も出ていました。したがって、多角形の形にもそれぞれの個性があるものと思われます。それでも十分面白いのですが、文章がヘッドの数程度の多角形の組み合わせでできていると思うとさらに面白いなという気持ちになります。
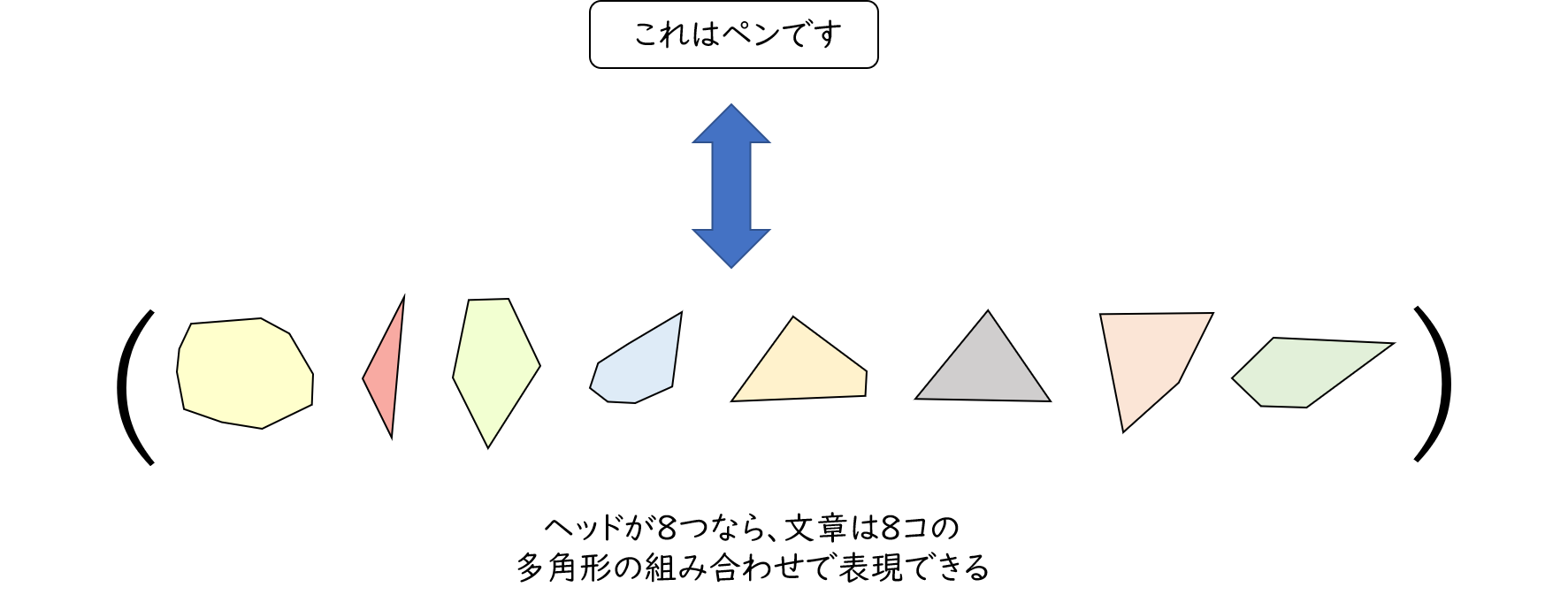
トランスフォーマーの中ではたくさんの多角形が伸び縮みしている?
ここまで、セルフアテンションの入出力が多角形と解釈できるという話を書いてきました。しかし、トランスフォーマーの内部で行われる計算は他にもあります。残差結合やフィードフォワード層による変換、活性化関数の適用などです。
非線形な変換も行われるとはいえ、内部で行われている主な処理は平行移動(残差結合)と投影、引き延ばし(フィードフォワード、活性化関数)です。そう考えるとトランスフォーマーの中ではセルフアテンションに限らずたくさんの多角形がたえず変化し続けているのではないでしょうか?(あくまでも僕個人の予想です。確かめたわけではありません。)
いつか人間が可視化できる程度の次元でトランスフォーマーを構築して、多角形がどう変化してくのかを観察できたらとても楽しいのではないかと思います。それくらいの技術を身に着けられるようにがんばりたいです。
最後まで読んでいただきありがとうございました!
数式が飛び交う中、最後まで読み進めていただき、ありがとうございました。
セルフアテンションを直感的にイメージできないか?という疑問から凸包という大道具を持ち出して多角形を眺めることになるとは勉強開始時は思いもしませんでした。凸包という概念を知っている人からすると今回の記事の結論は当たり前のことに感じたかもしれませんね。
でも少なくとも僕にとってはこの考え方は衝撃的で興味深いものでした。何より「なんじゃこりゃ?」から始まったセルフアテンションが、多角形というイメージ可能な対象になっただけでも考えてよかったな思います。
今後は次のようなことも考えてみたいです。
- セルフアテンションでできる図形に規則性はあるのか?
- トランスフォーマー内部の計算が進むたびに多角形はどう変化するのか?
- 文章の意味と多角形の形に関係はあるのか?
- 文章を意図的に多角形で表現する方法はないか?
- 文章をうまく記述する多角形の組み合わせがあった場合、その規則をつかって生成AIを作ることは可能か?
今回の記事の内容について、不備や矛盾などお気づきになった点があればご指摘いただけると助かります。また内容についてご質問等も歓迎しますので、よろしくお願いいたします。
参考文献ならびに参考図書
- Attention Is All You Need
- 山田育矢, 鈴木正敏, 山田康輔, 李凌寒, 「大規模言語モデル入門」, 技術評論社, 2023