はじめに
この記事は、Uplift Modeling for Multiple Treatments with Cost Optimization の内容をベースとしています。

余談ですが、執筆時2021年7月31日より幾月前からUber EatsさんがYouTube上で音声のない広告を流しています。とてもユーザの的を得ているように思えその発想にアルゴリズムが関与しているのであればとても興味深いです。
X-Learner & Extending X-Learner for Multiple Treatments
X-Learner と Extending X-Learner for Multiple Treatments それぞれのアルゴリズムを紹介します。
X-Learner の考え方は 2 つの段階に分けられます。
1 段階目では Treatment / Control それぞれの効果 $\mu_{1}, \ \mu_{0}$ を推定。
2 段階目では既に推定された効果と結果変数の差分を利用し条件付き期待値を算出。さらに傾向スコアで重みづけをすることで精度を高めています。
CATE の推定において「CATE がスパースな場合」「CATE の滑らかさ」「Treatment / Control 群の間に偏りがある場合」に対しある程度の対応をすることができます。
Extending X-Learner for Multiple Treatments は X-Learner を拡張し複数介入のケースにも対応できるようにした Meta-Learner のアルゴリズムです。
これはつまり「X-Learner は $t_j ∈ \{t_0, t_1\}$ を考えている」のに対し「Extending X-Learner for Multiple Treatments は $t_j ∈ \{t_0, t_1, ..., t_m\} \ (j ∈ \mathbb{Z})$ を考えている」ということを意味しています。
数式からも見て取れるように考え方の流れは X-Learner と同じです。
X-Learner
“pseudo-effects” ${D_{i}}$ for the observations in the control group as
\tilde{D_{i}^{0}} = \widehat{\mu }_{1}\left( x\right) - Y_{i}^{0} \tag{1}
and for the individuals in the treatment groups as
\tilde{D_{i}^{1}} = Y_{i}^{1} - \widehat{\mu }_{0}\left( x\right) \tag{2}
where ${Y_{i}}$ is the observed value for the user. The pseudo-effects are then used as the outcome in another pair of regression methods to obtain the response functions ${\tilde{\tau_{1}^{}}(x)}$ and ${\tilde{\tau_{1}^{}}(x)}$ for the control and treatment groups, respectively.
\begin{aligned}\widehat{\tau }\left( x\right) =e\left( x\right) \widehat{\tau }_{0}\left( x\right) +\left( 1-e\left( x\right) \right) \widehat{\tau }_{1}\left( x\right) \end{aligned} \tag{3}
where ${e(x)}$ is the propensity score $P[W_{i} = 1 \ | \ X_{i} = x]$ with ${W_{i}}$ indicating the treatment assignment.
Extending X-Learner for Multiple Treatments
Consider an experiment with a control group and m treatment groups. Here, we use any suitable regression method to estimate the response functions under each group:
\begin{aligned}\mu _{t_{j}}\left( x\right) = \mathbb{E}[ Y\left( t_{j}\right) \ | \ X=x] \end{aligned} \tag{4}
where $t_j ∈ \{t_0, t_1, ..., t_m\}$ with t0 denoting the control group.
We estimate ${\mu_{t_{0}}(x)}$ using data from the control group and${\mu_{t_{1}}(x)}$ using data from the j-th treatment group. We then proceed to estimate the pseudo-effects analogously,
{\begin{equation}
\begin{split}
\tilde{D_{i}^{t_{0}}} = \hat{\mu} _{t_{j}}(x) - Y_{i}
\\
\tilde{D_{i}^{t_{j}}} = Y_{i} - \hat{\mu} _{t_{0}}(x)
\end{split}
\end{equation}
} \tag{5}
where ${\tilde{D_{i}^{t_{0}}}}$ is estimated using control group data and ${\tilde{D_{i}^{t_{j}}}}$ is estimated using the data from the j-th treatment group. Finally, as in the two-group experiment, we use the pseudo-effects as
the outcomes in another pair of regressions to obtain $\hat{\tau} _{t_0}$ and $\hat{\tau}_{t_j}$.
In the multiple treatment group case, we need to estimate
the propensity score
e_{t_{j}}(x) \ = \ \mathbb{P}[W_{i} = t_{j} \ | \ X = x] \tag{6}
for each m experiment groups. Focusing on the case in which we compare each treatment group against the control, we then estimate the CATEor a given treatment group as follows :
\hat{\tau}^{t_{j}}(x) = \dfrac{\hat{e}_{t_j}(x)}{\hat{e}_{t_j}(x) + \hat{e}_{t_0}(x)}\hat{\tau}_{t_0}(x) \ + \ \dfrac{\hat{e}_{t_0}(x)}{\hat{e}_{t_j}(x) + \hat{e}_{t_0}(x)}\hat{\tau}_{t_j}(x) \tag{7}
Finally, to predict the best treatment group for an individual,
we estimate $\tau^{t_j}$ as
\hat{\tau}^{t_{j}}(X_i) = \dfrac{\hat{e}_{t_j}^{(-1)}(X_i)}{\hat{e}_{t_j}^{(-1)}(X_i) + \hat{e}_{t_0}^{(-1)}(X_i)}\hat{\tau}_{t_0}^{(-1)}(X_i) + \dfrac{\hat{e}_{t_0}^{(-1)}(X_i)}{\hat{e}_{t_j}^{(-1)}(X_i) + \hat{e}_{t_0}^{(-1)}(X_i)}\hat{\tau}_{t_j}^{(-1)}(X_i) \tag{8}
where notation of the form $\hat{e} _{t_j}^{(-1)}$ indicates that $\hat{e}_{t_j}$ has been estimated without using the $i$-th observation. We then simply compare which treatment group gives the highest predicted uplift for the individual and recommend that as the treatment group if the costs of treatments are equal.
Implementation
Check versions of libraries
import pandas
import numpy
import scipy
import sklearn
import lightgbm
import causalml
library_dict = {0: 'pandas', 1: 'numpy', 2: 'scipy', 3: 'sklearn', 4: 'lightgbm', 5: 'causalml'}
for num, library in enumerate([pandas, numpy, scipy, sklearn, lightgbm, causalml]):
print('{}: v{}'.format(library_dict[num], library.__version__))
>>
pandas: v1.3.1
numpy: v1.18.5
scipy: v1.4.1
sklearn: v0.23.2
lightgbm: v3.1.1
causalml: v0.10.0
X Learner execution class
import pandas as pd
import numpy as np
import sys
import logging
logger = logging.getLogger()
handler = logging.StreamHandler(sys.stdout)
handler.setLevel(logging.INFO)
logger.addHandler(handler)
logger.setLevel(logging.INFO)
import matplotlib.pyplot as plt
%matplotlib inline
from copy import deepcopy
from sklearn.model_selection import KFold, StratifiedKFold
from sklearn.metrics import mean_squared_error as mse
from sklearn.metrics import log_loss
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
import lightgbm as lgb
from causalml.dataset import synthetic_data, get_synthetic_summary_holdout
from causalml.propensity import compute_propensity_score
from causalml.metrics import plot, auuc_score
from causalml.inference.meta import BaseXRegressor
class XLearner(object):
def __init__(self, covariance_df: pd.core.frame.DataFrame, intervention_df: pd.core.frame.DataFrame) -> None:
"""
covariance_df: Covariate DataFrame.
intervention_df: Intervention DataFrame. If there are two types of interventions, three types of data will be stored together with the control.
"""
self.covariance_df = covariance_df
self.intervention_df = intervention_df
self.groups = list(self.intervention_df.iloc[:, 0].unique())
self.num_groups = len(self.groups)
def propensity_score_RF(self, n_splits: int, kfold_type: str):
self.n_splits = n_splits
self.kfold_type = kfold_type
self.preds_rf = {group_num: np.zeros(self.covariance_df.shape[0]) for group_num in range(self.num_groups)}
self.logloss_rf_train = {group_num: [] for group_num in range(self.num_groups)}
self.logloss_rf_valid = {group_num: [] for group_num in range(self.num_groups)}
if self.kfold_type == 'KFold':
self.c_v_instance = KFold(n_splits = self.n_splits, shuffle = False)
self.split = self.c_v_instance.split(self.covariance_df)
elif self.kfold_type == 'StratifiedKFold':
self.c_v_instance = StratifiedKFold(n_splits = self.n_splits, shuffle = True)
self.split = self.c_v_instance.split(self.covariance_df, self.intervention_df)
else:
raise Exception("kfold_type {} is invalid argument".format(self.kfold_type))
logger.info("RandomForestClassifier is progressing ...")
# self.valid_index_list = list()
for n_fold, (train_index, valid_index) in enumerate(self.split):
logger.info('{} Cross Validation {}'.format(self.kfold_type, n_fold))
# self.valid_index_list.extend(list(valid_index))
X_train, z_train = self.covariance_df.iloc[train_index], self.intervention_df.iloc[train_index]
X_valid, z_valid = self.covariance_df.iloc[valid_index], self.intervention_df.iloc[valid_index]
model_rf = RandomForestClassifier()
model_rf.fit(X_train, z_train.values.ravel())
pred_prob_train = {group_num: model_rf.predict_proba(X_train)[:, group_num] for group_num in range(self.num_groups)}
logloss_train = {group_num: log_loss(z_train, pred_prob_train[group_num]) for group_num in range(self.num_groups)}
[self.logloss_rf_train[group_num].append(logloss_train[group_num]) for group_num in range(self.num_groups)]
pred_prob_valid = {group_num: model_rf.predict_proba(X_valid)[:, group_num] for group_num in range(self.num_groups)}
logloss_valid = {group_num: log_loss(z_valid, pred_prob_valid[group_num]) for group_num in range(self.num_groups)}
[self.logloss_rf_valid[group_num].append(logloss_valid[group_num]) for group_num in range(self.num_groups)]
for group_num in range(self.num_groups):
self.preds_rf[group_num][valid_index] = pred_prob_valid[group_num]
self.logloss_rf_train_mean = {group_num: sum(self.logloss_rf_train[group_num]) / self.n_splits for group_num in range(self.num_groups)}
self.logloss_rf_valid_mean = {group_num: sum(self.logloss_rf_valid[group_num]) / self.n_splits for group_num in range(self.num_groups)}
self.eps = np.finfo(float).eps
self.preds_rf = {group_num: np.where(self.preds_rf[group_num] < 0 + self.eps, 0 + self.eps * 1.001, self.preds_rf[group_num]) for group_num in range(self.num_groups)}
self.preds_rf = {group_num: np.where(self.preds_rf[group_num] > 1 - self.eps, 1 - self.eps * 1.001, self.preds_rf[group_num]) for group_num in range(self.num_groups)}
logger.info("RandomForestClassifier is complete.")
return self.preds_rf, self.logloss_rf_train_mean, self.logloss_rf_valid_mean
def learners(self, learner, control_outcome_learner = None, treatment_outcome_learner = None, control_effect_learner = None, treatment_effect_learner = None) -> None:
self.learner = learner
self.control_outcome_learner = control_outcome_learner
self.treatment_outcome_learner = treatment_outcome_learner
self.control_effect_learner = control_effect_learner
self.treatment_effect_learner = treatment_effect_learner
def cate(self, target_df: pd.core.frame.DataFrame, intervention_col_name: str, covariance_col_name: list[str], target_col_name: str, ps_col_list: list[str], verbose: bool = False):
if self.control_outcome_learner is None:
self.model_mu_c = deepcopy(learner)
else:
self.model_mu_c = control_outcome_learner
if self.treatment_outcome_learner is None:
self.model_mu_t = deepcopy(learner)
else:
self.model_mu_t = treatment_outcome_learner
if self.control_effect_learner is None:
self.model_tau_c = deepcopy(learner)
else:
self.model_tau_c = control_effect_learner
if self.treatment_effect_learner is None:
self.model_tau_t = deepcopy(learner)
else:
self.model_tau_t = treatment_effect_learner
self.target_df = target_df
self.intervention_col_name = intervention_col_name
self.covariance_col_name = covariance_col_name
self.target_col_name = target_col_name
self.verbose = verbose
self.control_name = 0
self.t_groups = list(self.target_df[self.intervention_col_name].loc[self.target_df[self.intervention_col_name] != self.control_name].unique())
self.t_groups.sort() # ascending
self.ps = {group: np.array(self.target_df[ps_col]) for group, ps_col in enumerate(ps_col_list)}
self.te = np.zeros((self.target_df.shape[0], len(self.t_groups)))
self.dhat_cs = {}
self.dhat_ts = {}
self.models_mu_c = {group: deepcopy(self.model_mu_c) for group in self.t_groups}
self.models_mu_t = {group: deepcopy(self.model_mu_t) for group in self.t_groups}
self.models_tau_c = {group: deepcopy(self.model_tau_c) for group in self.t_groups}
self.models_tau_t = {group: deepcopy(self.model_tau_t) for group in self.t_groups}
for group in self.t_groups:
self.models_mu_c[group].fit(self.target_df.loc[self.target_df[self.intervention_col_name] == 0, self.covariance_col_name], self.target_df.loc[self.target_df[self.intervention_col_name] == 0, self.target_col_name])
self.models_mu_t[group].fit(self.target_df.loc[self.target_df[self.intervention_col_name] == group, self.covariance_col_name], self.target_df.loc[self.target_df[self.intervention_col_name] == group, self.target_col_name])
self.d_c = self.models_mu_t[group].predict(self.target_df.loc[self.target_df[self.intervention_col_name] == 0, self.covariance_col_name]) - self.target_df.loc[self.target_df[self.intervention_col_name] == 0, self.target_col_name]
self.d_t = self.target_df.loc[self.target_df[self.intervention_col_name] == group, self.target_col_name] - self.models_mu_c[group].predict(self.target_df.loc[self.target_df[self.intervention_col_name] == group, self.covariance_col_name])
self.models_tau_c[group].fit(self.target_df.loc[self.target_df[self.intervention_col_name] == 0, self.covariance_col_name], self.d_c)
self.models_tau_t[group].fit(self.target_df.loc[self.target_df[self.intervention_col_name] == group, self.covariance_col_name], self.d_t)
self.dhat_cs[group] = self.models_tau_c[group].predict(self.target_df[self.covariance_col_name])
self.dhat_ts[group] = self.models_tau_t[group].predict(self.target_df[self.covariance_col_name])
self.te_ = ((self.ps[group] / (self.ps[group] + self.ps[0])) * self.dhat_cs[group] + (self.ps[0] / (self.ps[group] + self.ps[0])) * self.dhat_ts[group]).reshape(-1, 1)
self.group_ = int(group) - 1
self.te[:, self.group_] = np.ravel(self.te_)
if self.verbose:
for group in self.t_groups:
logger.info("Treatment group: {}".format(group))
y_hat_control = self.models_mu_c[group].predict(self.target_df.loc[self.target_df[self.intervention_col_name] == 0, self.covariance_col_name])
y_hat_treatment = self.models_mu_t[group].predict(self.target_df.loc[self.target_df[self.intervention_col_name] == group, self.covariance_col_name])
# RMSE
rmse = np.sqrt(mse(np.array(self.target_df.loc[self.target_df[self.intervention_col_name] == 0, self.target_col_name]), np.array(y_hat_control)))
logger.info("RMSE Control: %s" %rmse)
rmse = np.sqrt(mse(np.array(self.target_df.loc[self.target_df[self.intervention_col_name] == group, self.target_col_name]), np.array(y_hat_treatment)))
logger.info("RMSE Treatment: %s" %rmse)
# Gini Coefficient
arr_control = np.array([np.array(self.target_df.loc[self.target_df[self.intervention_col_name] == 0, self.target_col_name]), y_hat_control]).transpose()
arr_treatment = np.array([np.array(self.target_df.loc[self.target_df[self.intervention_col_name] == group, self.target_col_name]), y_hat_treatment]).transpose()
for num, arr in enumerate([arr_control, arr_treatment]):
if num == 0:
n_samples = self.target_df.loc[self.target_df[self.intervention_col_name] == 0, self.target_col_name].shape[0]
elif num == 1:
n_samples = self.target_df.loc[self.target_df[self.intervention_col_name] == group, self.target_col_name].shape[0]
# sort rows on prediction column from largest to smallest
true_order = arr[arr[:, 0].argsort()][::-1, 0]
pred_order = arr[arr[:, 1].argsort()][::-1, 0]
# get Lorenz curves
l_true = np.cumsum(true_order) / np.sum(true_order)
l_pred = np.cumsum(pred_order) / np.sum(pred_order)
l_ones = np.linspace(1 / n_samples, 1, n_samples)
# get Gini coefficients, area between curves
g_true = np.sum(l_ones - l_true)
g_pred = np.sum(l_ones - l_pred)
# normalize to true Gini coefficient
true_gini = g_pred / g_true
if num == 0:
logger.info("Gini Control: %s" %true_gini)
elif num == 1:
logger.info("Gini Treatment: %s" %true_gini)
return self.te
y, X, treatment, _, _, e = synthetic_data(mode = 1, n = 10000, p = 5, sigma = 1.0)
synthetic_data_ = np.hstack(( y.reshape(len(y), 1), X, treatment.reshape(len(y), 1), e.reshape(len(y), 1) ))
synthetic_df = pd.DataFrame(data = synthetic_data_)
synthetic_df.rename(columns = {0 : 'Y', 1 : 'cova_1', 2 : 'cova_2',
3 : 'cova_3', 4 : 'cova_4', 5 : 'cova_5',
6 : 'inte', 7 : 'ps'},
inplace = True
)
covariance_df = synthetic_df[['cova_1', 'cova_2', 'cova_3', 'cova_4', 'cova_5']]
synthetic_df['inte'] = synthetic_df['inte'].astype(int)
intervention_df = synthetic_df['inte']
ins = XLearner(covariance_df, pd.DataFrame(intervention_df))
ps, logloss_rf_train, logloss_rf_valid = ins.propensity_score_RF(n_splits = 5, kfold_type = 'StratifiedKFold')
learner = lgb.LGBMRegressor(
boosting_type = 'gbdt',
objective = 'regression',
reg_alpha = 1,
reg_lambda = 1,
subsample = 0.6,
max_depth = 10,
num_leaves = 20,
colsample_bytree = 0.5,
min_child_weight = 10,
n_estimators = 1000
)
ins.learners(learner)
synthetic_df['ps_0'] = ps[0]
synthetic_df['ps_1'] = ps[1]
cate = ins.cate(synthetic_df, 'inte', ['cova_1', 'cova_2', 'cova_3', 'cova_4', 'cova_5'], 'Y', ['ps_0', 'ps_1'], True)
learner_x = BaseXRegressor(learner = learner)
cate_x = learner_x.fit_predict(X = X, treatment = treatment, y = synthetic_df['Y'], p = e, return_ci = False)
CATE
alpha = 0.2
bins = 30
plt.figure(figsize = (12, 8))
plt.hist(cate_x, alpha = alpha, bins = bins, label = 'X Learner')
plt.hist(cate, alpha = alpha, bins = bins, label = 'X Learner Multiple')
plt.legend()
plt.show()

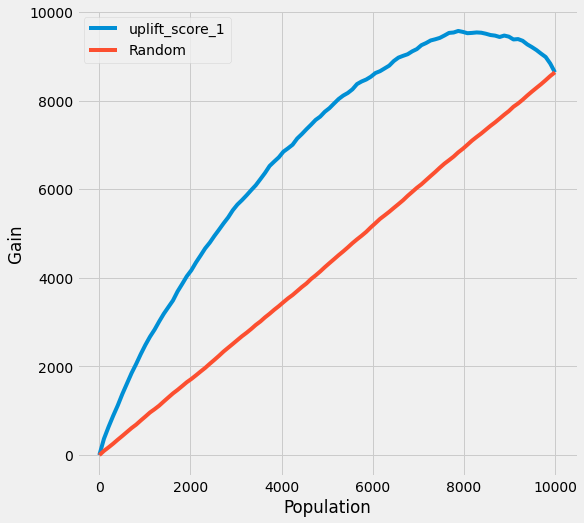
AUUC
synthetic_df['uplift_score_1'] = cate
# synthetic_df['uplift_score_causalml'] = cate_x
accu_score_ = auuc_score(df = synthetic_df[['Y','inte', 'uplift_score_1']], kind = 'gain',
outcome_col = 'Y',
treatment_col = 'inte')
logger.info('AUUC : %s' %accu_score_)
threshold_index = int(accu_score_.uplift_score_1 * synthetic_df.shape[0])
threshold = synthetic_df['uplift_score_1'].sort_values(ascending = False).reset_index(drop = True)[threshold_index]
logger.info('Threshold : %s' %threshold)
plot(df = synthetic_df[['Y','inte', 'uplift_score_1']], kind = 'gain',
outcome_col = 'Y',
treatment_col = 'inte'
)
# plot(df = synthetic_df[['Y','inte', 'uplift_score_causalml']], kind = 'gain',
# outcome_col = 'Y',
# treatment_col = 'inte'
# )
>>
AUUC : uplift_score_1 0.789995
Random 0.498822
dtype: float64
Threshold : -0.011212206037982897
まとめ
Uplift Modeling for Multiple Treatments with Cost Optimization の内容をもとに Extending X-Learner for Multiple Treatments を実装してみました。
認識や実装の間違いなどありましたらご指摘のほどよろしくお願いいたします。