この記事はKCS Advent Calendar 2025の2日目の記事です。
この記事について
もともと今年は Advent Calender を書く気はそんなになかったんですが、2日目から空いちゃってたので書きます。
なお、これを書いているのは12月1日の22時40分です。時間がそんなにない中急いで書いた記事なので、変なところがあっても許してください。
また、タグに Unity とありますが、本記事では Unity の話はほとんど出てきません。ご了承ください。
はじめに
先日、「プレゼント交換会用組み合わせ決めツール」なんてものをつくってみました。このアプリケーションは、名前の通りプレゼント交換会のような場において、交換する組み合わせを決めるためのツールです。Unity を用いて作成しました。
参加者名を入力し、各参加者がプレゼントを贈ることのできる参加者の情報を入力すると、条件を満たす組み合わせの一つが出力されます。
このアプリケーションは、KCS 内でクリスマスにでも開催しようと思っている「 steam ゲーム交換会」のために作成しました。基本的にプレゼント交換会においてはランダムに組み合わせを決めれば良いですが、「 steam ゲーム交換会」の場合はそうもいきません。なぜなら、steam のゲームを複数入手しても特に良いことはないためです。そのため、各参加者がもうすでに所持しているゲームを受け取らないような組み合わせを導き出す必要があります。このアプリケーションにおいては、この部分が実装されています。
GitHubにこのアプリケーションのデータをアップロードしています。公開しているので、気になる方は以下のリンクからダウンロードしてみてください。
https://github.com/Tomo271828/GiftExchanger
GiftExchanger.exe から実行できます。
自己紹介
情報工学科 3年
AtCoder:Tomo271828
KCS では昨年度ゲーム開発班と競プロ班の班長として活動
この組み合わせ探索が難しい理由
上に書いたように、基本的には組み合わせを乱択し、条件にあうかどうか判定することで問題なく組み合わせを発見できます。しかし、この条件に合う組み合わせが乱択できる全ての組み合わせと比較して非常に少ない場合、乱択では発見までに非常に長い時間がかかってしまうと考えられます。具体例としては、以下の場合などです。
上記の場合においては、全ての組み合わせが $10! = 3628800$ 通りもあるのに対し、条件を満たす組み合わせは上記の画像の $1$ 通りのみです。今回のアプリケーションでは $1$ 秒間に $30$ 通り程度しか探索できないため、乱択で上記の条件を満たすものを発見するのに非常に長い時間がかかることが予想されます。
これに加えて、条件を満たすものが存在しない入力も考えられます。具体的には、以下の場合などです。
上記のような場合においては、条件を満たす組み合わせが存在しないことが判明した時点で探索を打ち切らないと、処理が終わらなくなってしまいます。また、この存在しない条件として、「誰にもプレゼントを渡せない参加者がいる」「誰からもプレゼントを受け取れない参加者がいる」などの自明なものはいくつか考えられますが、上記の画像の例からわかるように、このような自明な条件では存在しない条件は記述できなそうです。
今回のアプリケーションにおいては、条件を満たす組み合わせが存在する場合は必ず10秒以内に1個発見し、存在しない場合はすぐに探索を打ち切るという実装をしています。ここまでの話を踏まえるとだいぶ不可能そうに思えますが、実装する方法は存在します。
問題の言い換え
最初に挙げた画像の入力を例として扱います。
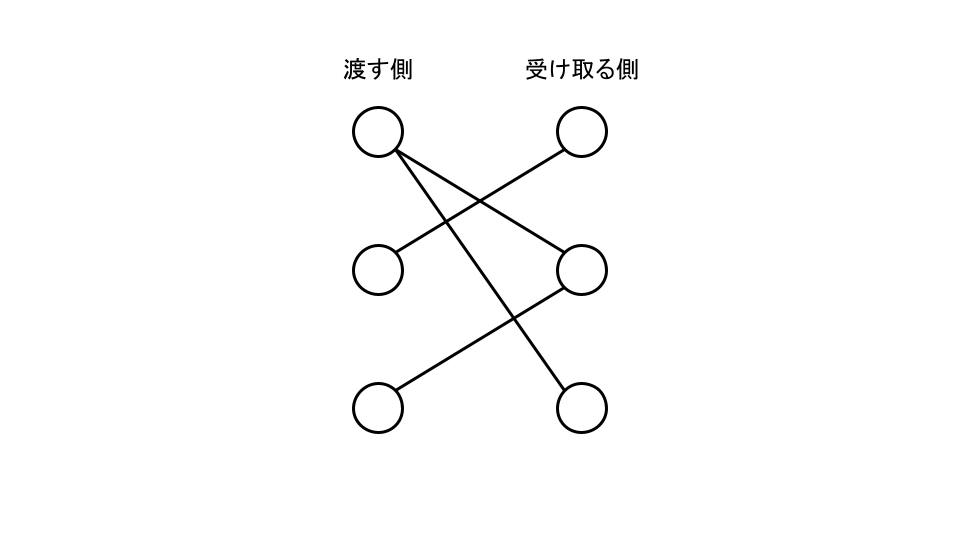
この入力を以下のようなグラフで表すことを考えます。
このグラフの各頂点はそれぞれ渡す側の各参加者か受け取る側の参加者を表し、各辺は渡すことのできる組を表しています。
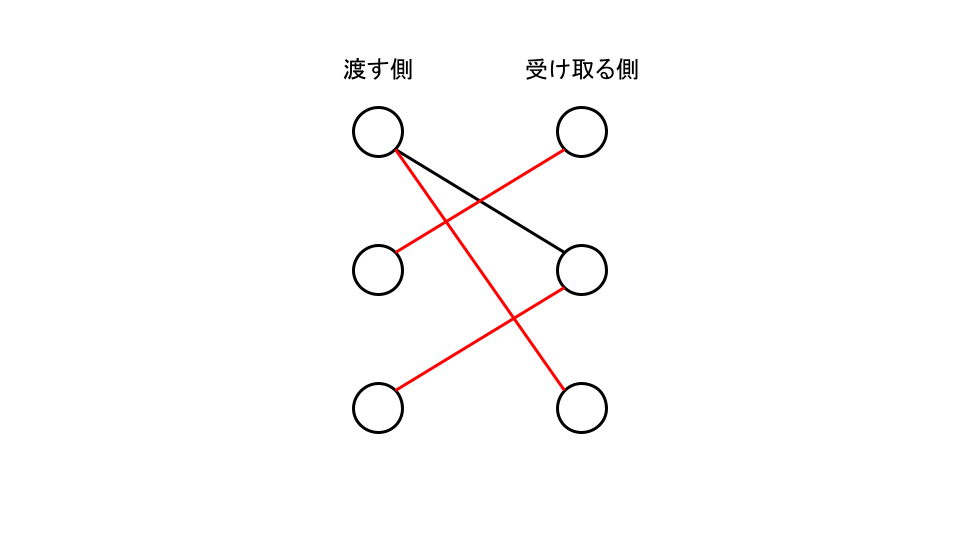
このグラフにおいて、各頂点がちょうど $1$ 本の辺の端点となるように、いくつかの辺を選ぶことを考えます。上記のグラフに対してこの操作を行ったものが以下のグラフです。
このような辺を選ぶ問題を最大 $2$ 部マッチング問題と呼びます。今回の問題においては、証明は省きますが、参加者が $N$ 人の場合、この最大 $2$ 部マッチングにおいて選ばれた辺の本数が $N$ 本である場合に条件を満たす組み合わせが存在し、この選ばれた $N$ 本の辺に対応する渡し方が条件を満たす渡し方の一つとなります。
問題の解法
ここまで来ればあとは適当にググれば解き方が分かります。
まず、上記のグラフに以下のように頂点を追加し、辺に重みを与え、向きをつけます。
証明は省略しますが、左端の頂点から右端の頂点に向けた最大フローの大きさが、求める最大 $2$ 部マッチングの大きさと一致します。この最大フローの大きさは Ford-Fullkerson 法などを用いることで求めることができるので、この問題を解くことができたと言えます。
実際の実装
ここまでの内容を踏まえて、実際のアプリケーションでは以下のような流れで処理をしています。
Ford-Fullkerson法で解の一つを導出
-> 10秒間乱択により探索、発見したら探索打ち切り
-> 10秒間発見できなかった場合、あらかじめ求めておいた解を出力
全体のプログラムも添付しておきます。
プログラム全体
using System;
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.UI;
using TMPro;
using System.Data;
using Unity.VisualScripting;
using System.Linq;
public class Data : MonoBehaviour
{
public int UserCount = 0;
public List<string> NameList = new List<string>();
public bool[,] ExchangeMap;
public bool Calculating;
}
public class AddRemovePlayer : MonoBehaviour
{
[SerializeField] TextMeshProUGUI errorMessage;
[SerializeField] Data data;
[SerializeField] GameObject nameInput; // 160 * 30
[SerializeField] GameObject checkBox; // 20 * 20
[SerializeField] GameObject targetTMP; // 200 * 30
[SerializeField] RectTransform scrollView;
List<GameObject> nameObjList = new List<GameObject>();
List<GameObject> targetList = new List<GameObject>();
List<List<GameObject>> checkBoxes = new List<List<GameObject>>();
string[] oneAnswer;
string calctext;
float count = 0.0f;
// Start is called before the first frame update
void Start()
{
data.Calculating = false;
}
// Update is called once per frame
void Update()
{
if (data.Calculating)
{
if (count >= 10)
{
for (int i = 0; i <= data.UserCount - 1; i++)
{
targetList[i].GetComponent<TextMeshProUGUI>().text = "→ " + oneAnswer[i];
}
data.Calculating = false;
errorMessage.text = "";
CancelInvoke();
return;
}
count += Time.deltaTime;
int n = data.UserCount;
List<int> list = new List<int>();
for (int i = 0; i <= n - 1; i++)
{
list.Add(i);
}
list = list.OrderBy(a => Guid.NewGuid()).ToList();
bool check = true;
for (int i = 0; i <= n - 1; i++)
{
if (!data.ExchangeMap[i, list[i]])
{
check = false;
break;
}
}
if (check)
{
for (int i = 0; i <= n - 1; i++)
{
targetList[i].GetComponent<TextMeshProUGUI>().text = "→ " + data.NameList[list[i]];
}
data.Calculating = false;
errorMessage.text = "";
CancelInvoke();
}
}
}
public void AddPlayer()
{
if (data.Calculating)
{
return;
}
if (data.UserCount >= 100)
{
ChangeErrorMessage("参加者が多すぎます!");
return;
}
for (int i = 0; i <= data.UserCount - 1; i++)
{
Destroy(targetList[i]);
}
targetList.Clear();
data.UserCount += 1;
checkBoxes.Add(new List<GameObject>());
scrollView.SetSizeWithCurrentAnchors(RectTransform.Axis.Horizontal, data.UserCount * 30 + 415);
scrollView.SetSizeWithCurrentAnchors(RectTransform.Axis.Vertical, data.UserCount * 30 + 20);
for (int i = 0; i <= data.UserCount - 2; i++)
{
GameObject toggle = Instantiate(checkBox);
RectTransform toggleRect = toggle.GetComponent<RectTransform>();
toggleRect.SetParent(scrollView,false);
Vector2 togglePosition = Vector2.zero;
togglePosition.x = (data.UserCount - 1) * 30 + 195;
togglePosition.y = i * -30 - 15;
toggleRect.localPosition = togglePosition;
checkBoxes[i].Add(toggle);
Toggle toggle_toggle = toggle.GetComponent<Toggle>();
toggle_toggle.isOn = true;
toggle_toggle.onValueChanged.AddListener(delegate { this.UpdateData(); });
}
for (int i = 0; i <= data.UserCount - 1; i++)
{
GameObject toggle = Instantiate(checkBox);
RectTransform toggleRect = toggle.GetComponent<RectTransform>();
toggleRect.SetParent(scrollView,false);
Vector2 togglePosition = Vector2.zero;
togglePosition.x = i * 30 + 195;
togglePosition.y = (data.UserCount - 1) * -30 - 15;
toggleRect.localPosition = togglePosition;
checkBoxes[data.UserCount - 1].Add(toggle);
Toggle toggle_toggle = toggle.GetComponent<Toggle>();
if (i == data.UserCount - 1)
{
toggle_toggle.isOn = false;
}
else
{
toggle_toggle.isOn = true;
}
toggle_toggle.onValueChanged.AddListener(delegate { this.UpdateData(); });
}
GameObject obj = Instantiate(nameInput);
RectTransform addRect = obj.GetComponent<RectTransform>();
addRect.SetParent(scrollView,false);
Vector2 position = Vector2.zero;
position.x = 10;
position.y = (data.UserCount - 1) * -30 - 10;
addRect.localPosition = position;
nameObjList.Add(obj);
TMP_InputField inputField = obj.GetComponent<TMP_InputField>();
inputField.text = "参加者" + data.UserCount.ToString("000");
inputField.onEndEdit.AddListener(delegate { this.UpdateData(); });
Debug.Log(inputField.text);
for (int i = 0; i <= data.UserCount - 1; i++)
{
GameObject targetText = Instantiate(targetTMP);
RectTransform targetRect = targetText.GetComponent<RectTransform>();
targetRect.SetParent(scrollView,false);
Vector2 targetPosition = Vector2.zero;
targetPosition.x = data.UserCount * 30 + 205;
targetPosition.y = i * -30 - 10;
targetRect.localPosition = targetPosition;
targetList.Add(targetText);
}
UpdateData();
}
public void RemovePlayer()
{
if (data.Calculating)
{
return;
}
if (data.UserCount <= 0)
{
return;
}
for (int i = 0; i <= data.UserCount - 2; i++)
{
Destroy(checkBoxes[i][data.UserCount - 1]);
checkBoxes[i].RemoveAt(data.UserCount - 1);
}
for (int i = 0; i <= data.UserCount - 1; i++)
{
Destroy(checkBoxes[data.UserCount - 1][i]);
Destroy(targetList[i]);
}
checkBoxes.RemoveAt(data.UserCount - 1);
targetList.Clear();
Destroy(nameObjList[data.UserCount - 1]);
nameObjList.RemoveAt(data.UserCount - 1);
data.UserCount -= 1;
scrollView.SetSizeWithCurrentAnchors(RectTransform.Axis.Vertical, data.UserCount * 30 + 20);
scrollView.SetSizeWithCurrentAnchors(RectTransform.Axis.Horizontal, data.UserCount * 30 + 415);
for (int i = 0; i <= data.UserCount - 1; i++)
{
GameObject targetText = Instantiate(targetTMP);
RectTransform targetRect = targetText.GetComponent<RectTransform>();
targetRect.SetParent(scrollView,false);
Vector2 targetPosition = Vector2.zero;
targetPosition.x = data.UserCount * 30 + 205;
targetPosition.y = i * -30 - 10;
targetRect.localPosition = targetPosition;
targetList.Add(targetText);
}
UpdateData();
}
public void UpdateData()
{
data.NameList.Clear();
foreach (GameObject obj in nameObjList)
{
RectTransform rect = obj.GetComponent<RectTransform>();
TextMeshProUGUI textBox = rect.Find("Text Area/Text").gameObject.GetComponent<TextMeshProUGUI>();
data.NameList.Add(textBox.text);
}
data.ExchangeMap = new bool[data.UserCount, data.UserCount];
string debug = "";
for (int i = 0; i <= data.UserCount - 1; i++)
{
for (int j = 0; j <= data.UserCount - 1; j++)
{
Toggle toggle = checkBoxes[i][j].GetComponent<Toggle>();
if (toggle.isOn)
{
data.ExchangeMap[i, j] = true;
debug += "o";
}
else
{
data.ExchangeMap[i, j] = false;
debug += "x";
}
}
debug += " ";
}
Debug.Log(debug);
}
void ChangeErrorMessage(string text)
{
errorMessage.text = text;
Invoke("ResetErrorMessage", 1.0f);
}
void ResetErrorMessage()
{
errorMessage.text = "";
}
public void Calculate()
{
int n = data.UserCount;
if (n <= 0)
{
ChangeErrorMessage("参加者がいません!");
return;
}
for (int i = 0; i <= n - 1; i++)
{
targetList[i].GetComponent<TextMeshProUGUI>().text = "→ ";
}
WeightedDirectedGraph graph = new WeightedDirectedGraph(n * 2 + 2);
for (int i = 0; i <= n - 1; i++)
{
for (int j = 0; j <= n - 1; j++)
{
if (data.ExchangeMap[i, j])
{
graph.AddEdge(i, j + n, 1);
}
}
graph.AddEdge(n * 2, i, 1);
graph.AddEdge(i + n, n * 2 + 1, 1);
}
long flow = graph.FordFulkerson(n * 2, n * 2 + 1);
if (flow < n)
{
ChangeErrorMessage("条件を満たす組み合わせは存在しません!");
return;
}
oneAnswer = new string[n];
HashSet<(int, int)> cut = graph.MinimumCut(n * 2, n * 2 + 1);
foreach ((int, int) edge in cut)
{
if (edge.Item1 < n && edge.Item2 >= n && edge.Item2 < n * 2)
{
int start = edge.Item1;
int goal = edge.Item2 - n;
oneAnswer[start] = data.NameList[goal];
}
}
data.Calculating = true;
count = 0.0f;
calctext = "計算中";
InvokeRepeating("CalculatingText", 0.0f, 1.0f);
}
void CalculatingText()
{
calctext += ".";
errorMessage.text = calctext;
}
}
class WeightedDirectedGraph
{
class Edge
{
public int start;
public int goal;
public long weight;
public Edge(int from, int to, long w)
{
this.start = from;
this.goal = to;
this.weight = w;
}
}
int n;
List<Edge>[] edgelist;
List<Edge>[] reverseedgelist;
List<Edge> allEdge;
public WeightedDirectedGraph(int node)
{
this.n = node;
this.edgelist = new List<Edge>[node];
this.reverseedgelist = new List<Edge>[node];
for(int i = 0;i <= node - 1; i++)
{
edgelist[i] = new List<Edge>();
reverseedgelist[i] = new List<Edge>();
}
allEdge = new List<Edge>();
}
public void AddEdge(int from,int to,long w)
{
Edge edge = new Edge(from, to, w);
allEdge.Add(edge);
edgelist[from].Add(edge);
reverseedgelist[to].Add(edge);
}
public long FordFulkerson(int start,int goal)
{
long[,] dist = new long[n, n];
var set = new HashSet<int>[n];
for(int i = 0;i <= n - 1; i++)
{
set[i] = new HashSet<int>();
}
foreach(Edge e in allEdge)
{
dist[e.start, e.goal] = Math.Max(dist[e.start, e.goal], e.weight);
if(e.weight > 0)
{
set[e.start].Add(e.goal);
}
}
long ret = 0;
while (true)
{
bool[] visited = new bool[n];
int[] from = new int[n];
Queue<int> queue = new Queue<int>();
queue.Enqueue(start);
while(queue.TryDequeue(out int node))
{
foreach(var i in set[node])
{
if (visited[i])
{
continue;
}
if (dist[node, i] <= 0)
{
continue;
}
visited[i] = true;
queue.Enqueue(i);
from[i] = node;
}
}
if (visited[goal])
{
int last = goal;
List<int> l = new List<int>();
l.Add(last);
while(last != start)
{
last = from[last];
l.Add(last);
}
long min = long.MaxValue;
for(int i = l.Count - 1;i >= 1; i--)
{
min = Math.Min(min, dist[l[i], l[i - 1]]);
}
for(int i = l.Count - 1;i >= 1; i--)
{
dist[l[i], l[i - 1]] -= min;
if (dist[l[i], l[i - 1]] <= 0)
{
set[l[i]].Remove(l[i - 1]);
}
dist[l[i - 1], l[i]] += min;
if (dist[l[i - 1],l[i]] >= 0)
{
set[l[i - 1]].Add(l[i]);
}
}
ret += min;
}
else
{
break;
}
}
return ret;
}
//カットされた辺集合を返す
public HashSet<(int, int)> MinimumCut(int start, int goal)
{
long[,] dist = new long[n, n];
var set = new HashSet<int>[n];
for (int i = 0; i <= n - 1; i++)
{
set[i] = new HashSet<int>();
}
foreach (Edge e in allEdge)
{
dist[e.start, e.goal] = Math.Max(dist[e.start, e.goal], e.weight);
if (e.weight > 0)
{
set[e.start].Add(e.goal);
}
}
while (true)
{
bool[] visited = new bool[n];
int[] from = new int[n];
Queue<int> queue = new Queue<int>();
queue.Enqueue(start);
while (queue.TryDequeue(out int node))
{
foreach (var i in set[node])
{
if (visited[i])
{
continue;
}
if (dist[node, i] <= 0)
{
continue;
}
visited[i] = true;
queue.Enqueue(i);
from[i] = node;
}
}
if (visited[goal])
{
int last = goal;
List<int> l = new List<int>();
l.Add(last);
while (last != start)
{
last = from[last];
l.Add(last);
}
long min = long.MaxValue;
for (int i = l.Count - 1; i >= 1; i--)
{
min = Math.Min(min, dist[l[i], l[i - 1]]);
}
for (int i = l.Count - 1; i >= 1; i--)
{
dist[l[i], l[i - 1]] -= min;
if (dist[l[i], l[i - 1]] <= 0)
{
set[l[i]].Remove(l[i - 1]);
}
dist[l[i - 1], l[i]] += min;
if (dist[l[i - 1], l[i]] >= 0)
{
set[l[i - 1]].Add(l[i]);
}
}
}
else
{
break;
}
}
HashSet<(int, int)> ret = new HashSet<(int, int)>();
foreach (Edge edge in allEdge)
{
if (dist[edge.start, edge.goal] == 0)
{
ret.Add((edge.start, edge.goal));
}
}
return ret;
}
}
このように実装することにより、目的の組み合わせ決めツールを作ることができました。
終わりに
今回紹介した「プレゼント交換会用組み合わせ決めツール」においては、Unity 製のアプリケーションでありながら、裏ではアルゴリズムの知識を用いています。
これまでの Unity での開発において、このようなアルゴリズムの知識を用いたことはほとんどないですが、今回のような場合もごくまれにあるので、競技プログラミングの経験が Unity での開発に活きることもあると言えると思います。
ちなみに今の時間は12月2日0時50分です。ちょっとすぎましたが12月2日までに書き終わって良かったです。
参考文献
- 二部グラフの最大マッチングと増加道, https://manabitimes.jp/math/1147
- Ford-Fullkerson法による最大フローの値を求めるアルゴリズム, https://algo-logic.info/ford-fullkerson/