【FDTD解説シリーズ②】FDTDのもう一歩深くへ

前回の記事では電磁界解析で用いられるFDTDの理論を説明しました。
今回は少し踏み込んで物性と境界条件の話。

導電率と導磁率

前回のマクスウェル方程式には導電率や導磁率がありませんでした。導体中の解析ができないんですね。PEC(Perfect Electric Conductor)しか解析しない場合は特に問題ありませんが、より一般化するために導入しましょう。
この先吸収境界条件を扱うためにも必須の作業です。

やることは簡単です。まず、前回のマクスウェル方程式のうち回転系の2式に対して、導電率を$\sigma$と導磁率$\sigma_m$を導入します。導磁率は磁流の流れやすさです。磁流は電流の対にあたる仮想概念で、実際には存在しません。なので導磁率も存在しませんが、この項があるとこの先便利なので導入します。すると、回転系のマクスウェル方程式は以下のように書き換わります。

\begin{align}
\nabla\times\boldsymbol{E} &= -\mu\frac{\partial\boldsymbol{H}}{\partial t} - \boldsymbol{J_m}\\
\nabla\times\boldsymbol{H} &= \varepsilon\frac{\partial\boldsymbol{E}}{\partial t} + \boldsymbol{J}\\
\end{align}

そして、前回謎に終わった方も多いであろう変位電流$\boldsymbol{J}$ですが、これは外部からの印加電流密度$\boldsymbol{J_0}$と、オームの法則による導体中の電流$\sigma \boldsymbol{E}$に分けられます。同じく磁場に対しても仮想的にオームの法則を適応します。

\begin{align}
\nabla\times\boldsymbol{E} &= -\mu\frac{\partial\boldsymbol{H}}{\partial t} - \boldsymbol{J_{m0}} - \sigma_m\boldsymbol{H}\\
\nabla\times\boldsymbol{H} &= \varepsilon\frac{\partial\boldsymbol{E}}{\partial t} + \boldsymbol{J_0} + \sigma\boldsymbol{E}\\
\end{align}

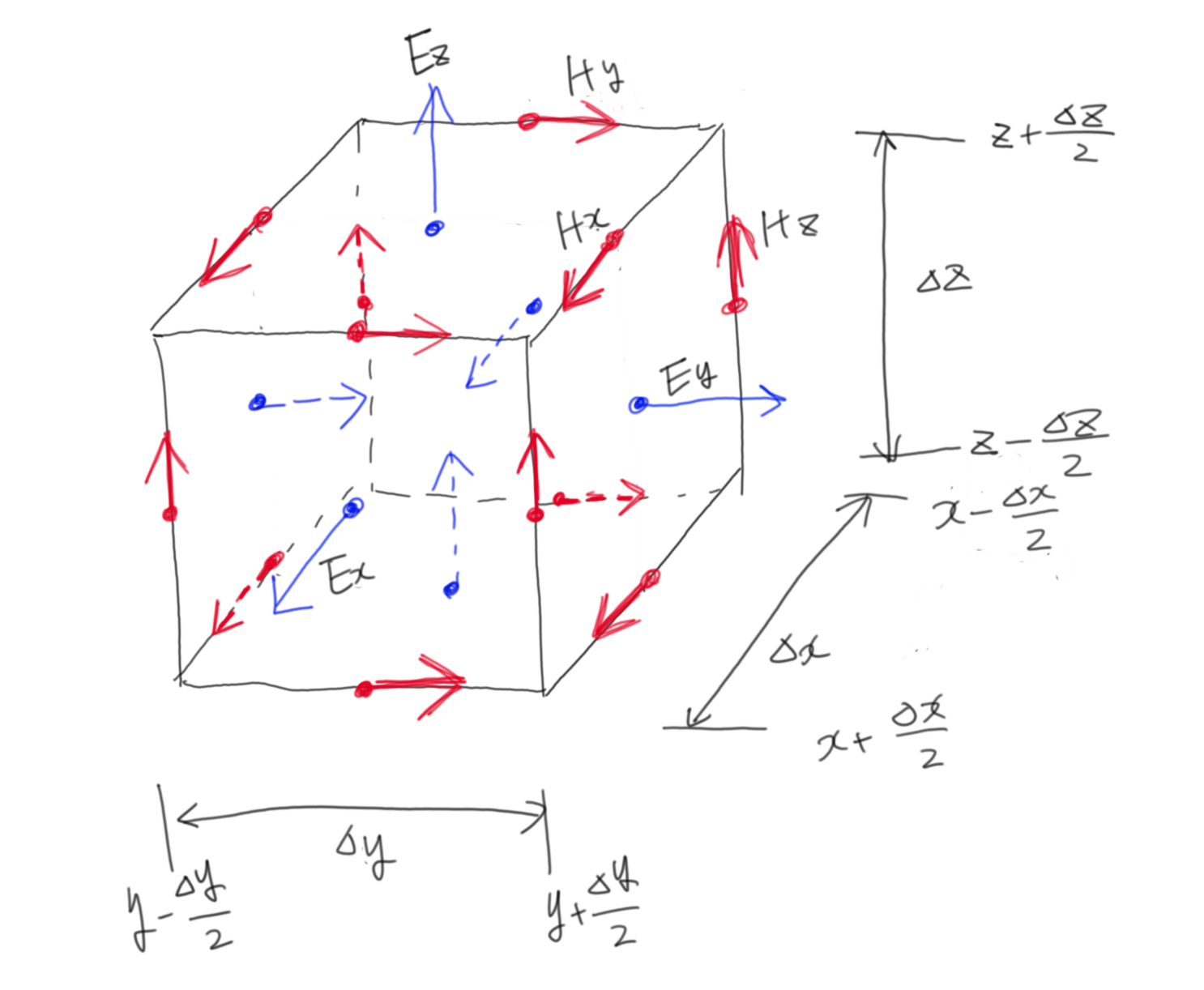
この条件でもう一回マクスウェル方程式の離散化を行います。Yeeセルは以下の通り。

とりあえず$E_x$について離散化してみます。前回式が長くなってしまったので、今回は時間$t(n)$で、位置(x(i),y(j),z(k))の電界を$E_{x,i,j,k}^n$と書くことにします。セルの一辺はdとします。

\begin{align}
\varepsilon\frac{E_{x,i+1/2,j,k}^{n+1}-E_{x,i+1/2,j,k}^n}{\Delta t}+J_{0x}+\sigma E_{x,i+1/2,j,k}^{n+1}
&=
\frac{H_{z,i+1/2,j+1/2,k}^{n+1/2}-H_{z,i+1/2,j-1/2,k}^{n+1/2}}{d}-\frac{H_{y,i+1/2,j,k+1/2}^{n+1/2}-H_{y,i+1/2,j,k-1/2}^{n+1/2}}{d}\\
\Rightarrow E_{x,i+1/2,j,k}^{n+1} &= \frac{\varepsilon}{\varepsilon+\sigma\Delta t}E_{x,i+1/2,j,k}^n-\frac{\varepsilon\Delta t}{\varepsilon+\sigma\Delta t}J_{0x}\\
&+\frac{\Delta t}{d(\varepsilon+\sigma\Delta t)}\left[H_{z,i+1/2,j+1/2,k}^{n+1/2}-H_{z,i+1/2,j-1/2,k}^{n+1/2}-H_{y,i+1/2,j,k+1/2}^{n+1/2}+H_{y,i+1/2,j,k-1/2}^{n+1/2}\right]
\end{align}

この調子で$E_y$は

\begin{align}
\varepsilon\frac{E_{y,i,j+1/2,k}^{n+1}-E_{y,i,j+1/2,k}^n}{\Delta t}+J_{0y}+\sigma E_{y,i,j+1/2,k}^{n+1}
&=
\frac{H_{x,i,j+1/2,k+1/2}^{n+1/2}-H_{x,i,j+1/2,k-1/2}^{n+1/2}}{d}-\frac{H_{z,i+1/2,j+1/2,k}^{n+1/2}-H_{z,i+1/2,j-1/2,k}^{n+1/2}}{d}\\
\Rightarrow E_{y,i,j+1/2,k}^{n+1} &= \frac{\varepsilon}{\varepsilon+\sigma\Delta t}E_{y,i,j+1/2,k}^n-\frac{\varepsilon\Delta t}{\varepsilon+\sigma\Delta t}J_{0y}\\
&+\frac{\Delta t}{d(\varepsilon+\sigma\Delta t)}\left[H_{x,i,j+1/2,k+1/2}^{n+1/2}-H_{x,i,j+1/2,k-1/2}^{n+1/2}-H_{z,i+1/2,j+1/2,k}^{n+1/2}+H_{z,i+1/2,j-1/2,k}^{n+1/2}\right]
\end{align}

$E_z$は、、、(疲れた)

\begin{align}
\varepsilon\frac{E_{z,i,j,k+1/2}^{n+1}-E_{z,i,j,k+1/2}^n}{\Delta t}+J_{0z}+\sigma E_{z,i,j,k+1/2}^{n+1}
&=
\frac{H_{y,i+1/2,j,k+1/2}^{n+1/2}-H_{y,i-1/2,j,k+1/2}^{n+1/2}}{d}-\frac{H_{x,i,j+1/2,k+1/2}^{n+1/2}-H_{x,i,j-1/2,k+1/2}^{n+1/2}}{d}\\
\Rightarrow E_{z,i,j,k+1/2}^{n+1} &= \frac{\varepsilon}{\varepsilon+\sigma\Delta t}E_{z,i,j,k+1/2}^n-\frac{\varepsilon\Delta t}{\varepsilon+\sigma\Delta t}J_{0z}\\
&+\frac{\Delta t}{d(\varepsilon+\sigma\Delta t)}\left[H_{y,i+1/2,j,k+1/2}^{n+1/2}-H_{y,i-1/2,j,k+1/2}^{n+1/2}-H_{x,i,j+1/2,k+1/2}^{n+1/2}+H_{x,i,j-1/2,k+1/2}^{n+1/2}\right]
\end{align}

続いて磁場

\begin{align}
-\mu\frac{H_{x,i,j+1/2,k+1/2}^{n+1/2}-H_{x,i,j+1/2,k+1/2}^{n-1/2}}{\Delta t}-J_{m0x}-\sigma_m H_{x,i,j+1/2,k+1/2}^{n+1/2}
&=
\frac{E_{z,i,j+1,k+1/2}^{n}-E_{z,i,j,k+1/2}^{n}}{d}-\frac{E_{y,i,j+1/2,k+1}^{n}-E_{y,i,j+1/2,k}^{n}}{d}\\
\Rightarrow H_{x,i,j+1/2,k+1/2}^{n+1/2} &= \frac{\mu}{\mu+\sigma_m\Delta t}H_{x,i,j+1/2,k+1/2}^{n-1/2}-\frac{\mu\Delta t}{\mu+\sigma_m\Delta t}J_{m0x}\\
&+\frac{\Delta t}{d(\mu+\sigma_m\Delta t)}\left[E_{z,i,j+1,k+1/2}^{n}-E_{z,i,j,k+1/2}^{n}-E_{y,i,j+1/2,k+1}^{n}+E_{y,i,j+1/2,k}^{n}\right]\\

-\mu\frac{H_{y,i+1/2,j,k+1/2}^{n+1/2}-H_{y,i+1/2,j,k+1/2}^{n-1/2}}{\Delta t}-J_{m0y}-\sigma_m H_{y,i+1/2,j,k+1/2}^{n+1/2}
&=
\frac{E_{x,i+1/2,j,k+1}^{n}-E_{x,i+1/2,j,k}^{n}}{d}-\frac{E_{z,i+1,y,z+1/2}^{n}-E_{z,i,y,z+1/2}^{n}}{d}\\
\Rightarrow H_{y,i+1/2,j,k+1/2}^{n+1/2} &= \frac{\mu}{\mu+\sigma_m\Delta t}H_{y,i+1/2,j,k+1/2}^{n-1/2}-\frac{\mu\Delta t}{\mu+\sigma_m\Delta t}J_{m0y}\\
&+\frac{\Delta t}{d(\mu+\sigma_m\Delta t)}\left[E_{x,i+1/2,j,k+1}^{n}-E_{x,i+1/2,j,k}^{n}-E_{z,i+1,y,z+1/2}^{n}+E_{z,i,y,z+1/2}^{n}\right]\\

-\mu\frac{H_{z,i+1/2,j+1/2,k}^{n+1/2}-H_{z,i+1/2,j+1/2,k}^{n-1/2}}{\Delta t}-J_{m0z}-\sigma_m H_{z,i+1/2,j+1/2,k}^{n+1/2}
&=
\frac{E_{y,i+1,j+1/2,k}^{n}-E_{y,i,j+1/2,k}^{n}}{d}-\frac{E_{x,i+1/2,j+1,k}^{n}-E_{x,i+1/2,j,k}^{n}}{d}\\
\Rightarrow H_{z,i+1/2,j+1/2,k}^{n+1/2} &= \frac{\mu}{\mu+\sigma_m\Delta t}H_{z,i+1/2,j+1/2,k}^{n-1/2}-\frac{\mu\Delta t}{\mu+\sigma_m\Delta t}J_{m0z}\\
&+\frac{\Delta t}{d(\mu+\sigma_m\Delta t)}\left[E_{y,i+1,j+1/2,k}^{n}-E_{y,i,j+1/2,k}^{n}-E_{x,i+1/2,j+1,k}^{n}+E_{x,i+1/2,j,k}^{n}\right]
\end{align}

ちなみにマクスウェル方程式第二式より、磁場の湧き出しはないので、実際には印加磁流$\boldsymbol{J_{m0}}$は存在しませんが、仮想的につけた方が色が対称的で計算しやすいことがあります。FDTDでは磁流の概念は使いませんがヘルムホルツ方程式を解く時など、便宜上登場することがあるので覚えておきましょう。
あと、上の式についてミスがあったら編集リクエストお願いします。

#PECとPMC
話は変わって導体の解析ですが、導体の厚さが比較的分厚い(表皮効果で検索！)もしくはロスが小さい場合は、導電率を用いずにPEC境界を用いることが多いです。回路配線などには使わない方が吉な気がしますが、アンテナ素子設計など導電率によるロスがほぼ無視できる場合はよく使う条件です。物性的にいえば導電率と誘電率が$\infty$、透磁率が1で導磁率0の物質です。

PECは上でチラッと出てきた通りPerfect Electric Conductorの略です。電場はPEC表面で全反射され、電流も表面しか流れないので、PEC内部には電場が発生しません。実装の際はPECの表面にあたるYeeセルの面の電場をゼロに固定すればよく、PECで閉じた形状の場合は物体内部の電場を全てゼロに固定すれば良いです。

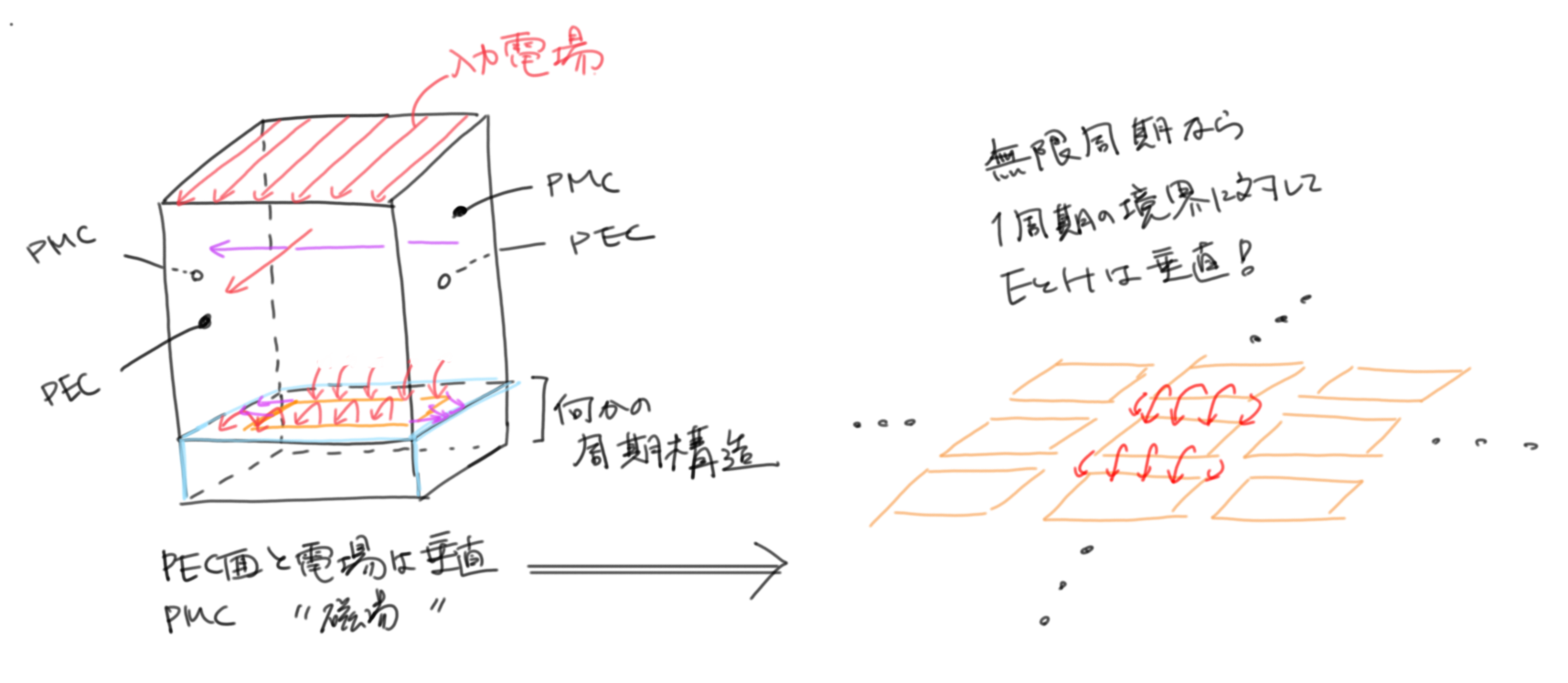
PMCはPECの磁場版で、Perfect Magnetic Conductorです。実際にそんな物質はありませんが、性質の便利さゆえにアンテナ解析などでよく使われます。理屈は上のPECの説明中の”電場”を”磁場”に読み替えていただければいいです。

PMCは何が便利かというと、周期構造の解析に便利なのです。世の中では電波吸収体などの解析で使われます。ある周期構造の1周期構造に対して垂直に平面波¹が入射する場合、電場と垂直な面にPEC、磁場と垂直な面にPMCを貼ることで、電磁界的にも無限周期かつ平面波入射の状態が作れます。

#異方性材料
吸収境界の前に、異方性の物質による離散化式への影響を考えます。異方性物質とは、電場や磁場の進行方向によって異なる物性を持つ材料のことで、BerengerのPMLにも登場します。変数上では$\varepsilon_x,\varepsilon_y,\varepsilon_z$を用意すればいいだけですが、式の上ではかなり複雑になります。

「マクスウェル方程式の誘電率とかを書き換えるだけじゃん」と甘くみないでください。重要なのは異方性材料は「進行方向によって異なる物性を持つ」という点です。電磁波の進行方向とはポインティングの定理より、

\boldsymbol{S} = \boldsymbol{E}\times\boldsymbol{H}

で決まります。$\boldsymbol{S}$は電磁波の進行方向と電力密度を表すベクトルです。上の式から、電場だけ求まっていても、その電力は電場に垂直方向に進むということしかわからず、具体的な方位が定まりません。方向を求めるには磁場の向きも必要なわけですが、FDTDの離散化では都合よく分解できます。以下の式をみてください。

\begin{align}
E_{x,i+1/2,j,k}^{n+1} &= \frac{\varepsilon}{\varepsilon+\sigma\Delta t}E_{x,i+1/2,j,k}^n-\frac{\varepsilon\Delta t}{\varepsilon+\sigma\Delta t}J_{0x}\\
&+\frac{\Delta t}{d(\varepsilon+\sigma\Delta t)}\left[H_{z,i+1/2,j+1/2,k}^{n+1/2}-H_{z,i+1/2,j-1/2,k}^{n+1/2}-H_{y,i+1/2,j,k+1/2}^{n+1/2}+H_{y,i+1/2,j,k-1/2}^{n+1/2}\right]
\end{align}

これを見ると、$E_x$については$H_y,H_z$で求められるわけなので、$E_x$の式中でz方向に伝搬する成分と、z方向に伝搬する成分に分けることができます。すると以下のように異方性の物性値を使って記述ができます。ここではy方向に伝搬する$E_x$成分を$E_{xy}$と書くことにします。

\begin{align}
E_{xy,i+1/2,j,k}^{n+1} &= \frac{\varepsilon_y}{\varepsilon_y+\sigma_y\Delta t}E_{xy,i+1/2,j,k}^n-\frac{\varepsilon_y\Delta t}{\varepsilon_y+\sigma_y\Delta t}J_{0xy}
+\frac{\Delta t}{d(\varepsilon_y+\sigma_y\Delta t)}\left[H_{z,i+1/2,j+1/2,k}^{n+1/2}-H_{z,i+1/2,j-1/2,k}^{n+1/2}\right]\\
E_{xz,i+1/2,j,k}^{n+1} &= \frac{\varepsilon_z}{\varepsilon_z+\sigma_z\Delta t}E_{xz,i+1/2,j,k}^n-\frac{\varepsilon_z\Delta t}{\varepsilon_z+\sigma_z\Delta t}J_{0xz}
-\frac{\Delta t}{d(\varepsilon_z+\sigma_z\Delta t)}\left[H_{y,i+1/2,j,k+1/2}^{n+1/2}-H_{y,i+1/2,j,k-1/2}^{n+1/2}\right]
\end{align}

こんな感じで電場磁場合わせて6つあった離散化式は、異方性物質を扱うことによって12こになります。ちなみに$E_x=E_{xy}+E_{xz}$です。磁場についても同じように成分分解できますので、計算してみてください。

#BerenerのPML
今回の難関”吸収境界条件”です。FDTDで使われる吸収境界はいくつかありますが、今回は最もメジャーであろうBerengerの条件を解説します。異方性材料を理解してから進んだ方がいいでしょう。

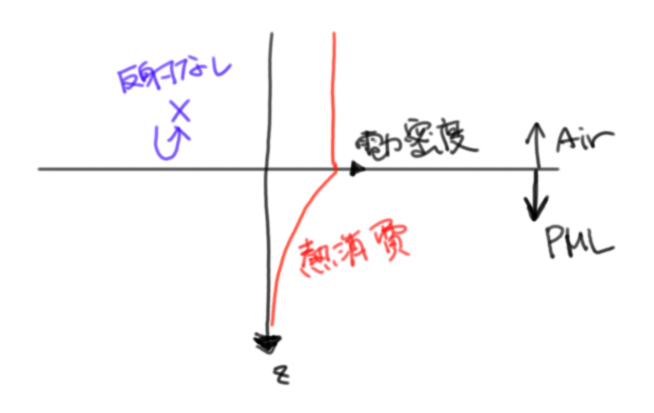
そもそもPMLはPerfect Matched Layerであり、境界条件ではありません。便宜上吸収境界と呼んでいますが、正体は以下のような材料です。

• PMLと隣接する材料とのインピーダンスが同じである。これを満たさないと境界面で反射電力が生じる。
• PML内でほぼ全ての電力が熱消費される。

イメージ的には、PMLに突入してからPMLの終端に行くまでに連続的に熱消費率が上がっていき、しまいに全部消費される感じです。連続的に熱消費率を上げる部分でいろいろな手法があり、BerengerのPMLはよく使われる条件の一つです。

説明を読んでわかると思いますが、現実にPMLは存在しません。伝搬方向によって物性が変わるので、シミュレーションのみで使用できる仮想的な異方性材料です。

##熱消費率の制御
PMLは基本的に異方性誘電体なわけですが、熱消費とはどういうことでしょう。これは複素誘電率、複素透磁率という概念で決定されます。
そもそも電磁波におけるインピーダンスとは電場と磁場の比ですが、いったんマクスウェル方程式を解いてみます。まず以下のベクトル公式

{\rm rot}({\rm rot}\boldsymbol{V}) = {\rm grad}({\rm div}\boldsymbol{V})-\nabla^2\boldsymbol{V}

を印加磁流のない電場のマクスウェルに応用して、${\rm rot}$を取ってみます

\begin{align}
\nabla\times(\nabla\times\boldsymbol{E}) = -\mu\frac{\partial}{\partial t}{\rm rot}\boldsymbol{H}
\end{align}

${\rm rot}\boldsymbol{H}$に変位電流のない磁場の回転系のマクスウェルを代入すると、

\begin{align}
{\rm grad}(\nabla\cdot\boldsymbol{E})-\nabla^2\boldsymbol{E} = -\varepsilon\mu\frac{\partial^2\boldsymbol{E}}{\partial t^2}
\end{align}

となり、結局

\begin{align}
\nabla^2\boldsymbol{E} = \varepsilon\mu\frac{\partial^2\boldsymbol{E}}{\partial t^2}
\end{align}

が得られます。変位電流があった場合は

\begin{align}
\nabla^2\boldsymbol{E} = \frac{\partial}{\partial t}\left(\mu\sigma\boldsymbol{E}+\varepsilon\mu\frac{\partial\boldsymbol{E}}{\partial t}\right)
\end{align}

ここで、$\boldsymbol{E}(\boldsymbol{r},t) = \boldsymbol{E}(\boldsymbol{r}){\rm exp}(j\omega t)$としてみると

\begin{align}
(\nabla^2+\varepsilon\mu\omega^2-j\omega\mu\sigma)\boldsymbol{E}(\boldsymbol{r})=0
\end{align}

ややこしいのでx方向のみ考えてみると

\begin{align}
\frac{\partial^2E_x}{\partial x^2} = \omega^2\mu(\varepsilon-j\frac{\sigma}{\omega})E_x
\end{align}

とりあえずこの解を$Ex=f(x-ct)$としておいて磁場を同じ要領で求めると$H_y=g(y-ct)$となりまして、この2つをマクスウェル方程式に代入すると

E_x = \sqrt{\frac{\mu - j\sigma_m/\omega}{\varepsilon - j\sigma/\omega}}H_y

となります。この$\sqrt{\frac{\mu - j\sigma_m/\omega}{\varepsilon - j\sigma/\omega}}$が電磁波のインピーダンスです。波動方程式で伝搬するものですので、虚部があると位相ズレが生じ、その分が熱損失になります。PMLの設計では導電率や導磁率を使って熱消費させつつ、境界面ではインピーダンスマッチングするようにします。

ちなみに、$\mu - j\sigma_m/\omega$を複素透磁率、$\varepsilon - j\sigma/\omega$を複素誘電率と言います。

---

本題に戻ってBerengerのPMLではどう設計されているかというと

\frac{\sigma}{\varepsilon} = \frac{\sigma_m}{\mu}

となるようにします。これによってインピーダンスは

\sqrt{\frac{\mu - j\mu\sigma/\varepsilon\omega}{\varepsilon - j\sigma/\omega}} = \sqrt{\frac{\mu}{\varepsilon}}

となって、解析空間内のインピーダンスと周波数に関係なくマッチングします。あとはPMLの深さに応じて導電率や導磁率を動かすだけです。
z方向にPMLを貼る場合を考えて、PMLの表面からの深さを$z$, PML全体の厚さを$z_M$, PMLの一番外側の導電率を$\sigma_M$とした時

\sigma(z)=\sigma_M\left(\frac{z}{z_M}\right)^m

となるようにします。入射角$\theta$の時、PMLからの反射率は

R(\theta) = {\rm exp}\left(-\frac{2}{m+1}\frac{z_M\sigma_M}{\sqrt{\varepsilon/\mu}}\cos{\theta}\right)

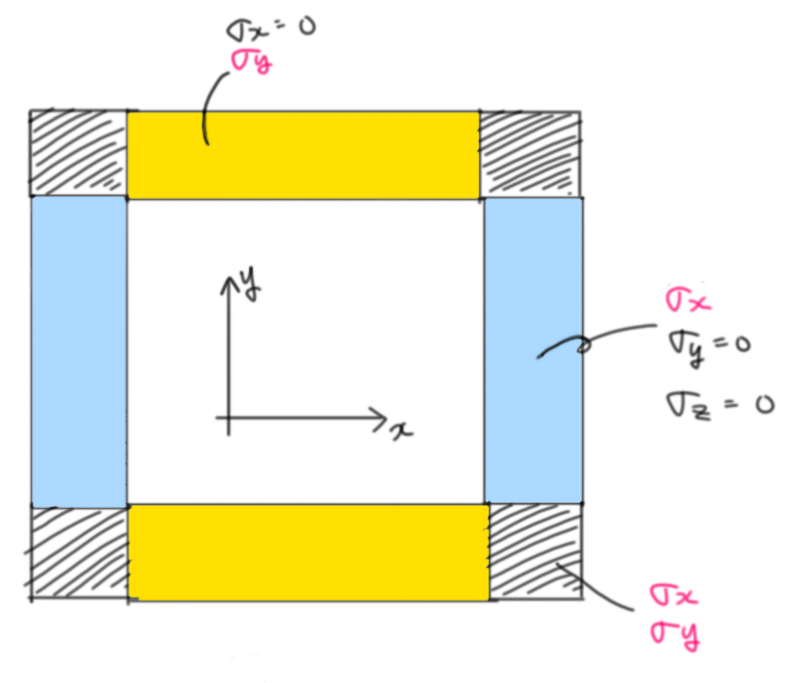
となることが知られているので、$R$の値を設定して導電率を求め、それに合わせた導磁率を設定するという流れでBerengerのPMLの完成です。z方向の伝搬にはz方向のPMLを、xにはx方向の物を。。。という感じで異方性材料として設定するため、以下のように設定します。これがあるので異方性材料を理解しないといけなかったんですよ。お疲れ様です。

#まとめ
今回は材料と境界条件について説明しました。長すぎて式を全部書けないところもありましたが、仕組みを理解できたら次は実装です。実装はさすがに2次元でやります。

次回の記事はこちら
【FDTD解説シリーズ③】電磁界FDTDを実装しよう

1. 電磁波は基本的に球面上に広がるので同位相面が平面になることはないが、無限遠に波源があると、伝搬する球面の曲率が無限大となり、電磁波の同相面は平面であるかのように見える。 ↩