【FDTD解説シリーズ①】FDTDで電磁界解析基礎
【FDTD解説シリーズ②】FDTDのもう一歩深くへ
と、FDTDの理論と物性について解説しました。今回はそれを実装します。
MATLABを使って実装しますが、3D-FDTDは遅いので今回は簡潔にするため、$xy$面で$H_z, E_x, E_y$のみが存在する2D-FDTDとします。
用意するモノ
FDTD解析で用意するものは以下の通りです。
- 電場配列: セル数 x セル数 (x,yの2成分)
- 印加電流密度: セル数 x セル数 (x,yの2成分)
- 磁場配列: セル数 x セル数 (z成分のみだが、xに進行する成分とyに進行する成分とその和が必要)
- 異方性誘電率配列: セル数 x セル数 (x,yの2成分)
- 異方性導電率配列: セル数 x セル数 (x,yの2成分)
- 異方性透磁率配列: セル数 x セル数 (x,yの2成分)
- 異方性導磁率配列: セル数 x セル数 (x,yの2成分)
- 座標: セル数 x セル数 (x,yの2成分)
物性を異方性としているのはPMLを考慮してのことです。メモリに配慮するならこの辺は最適化できそうです。電場磁場に関しては前の時間ステップの分も必要です。
そして電場磁場ですが、Yeeセルのままだと配列にしにくくてしょうがないので、今回は$E_{x,i+1/2,j,k}^n, E_{y,i,j+1/2,k}^n$を電場配列の(idx,idy)に格納します。同じく$H_{z,i+1/2,j+1/2,k}^n$を磁場の(idx,idy)に格納します。今回は2D-FDTDということで$k$は関係ないので、この表記で式を書き直すと、
\begin{align}
E_{x,idx,idy}^{n+1} &= A_{sy}E_{x,idx,idy}^n-B_{sy}J_{0xy}+C_{sy}\left[H_{z,idx,jdy}^{n+1/2}-H_{z,idx,idy-1,k}^{n+1/2}\right]\\
E_{y,idx,idy}^{n+1} &= A_{sx}E_{y,idx,idy}^n-B_{sx}J_{0yx}-C_{sx}\left[H_{z,idx,idy}^{n+1/2}-H_{z,idx-1,idy}^{n+1/2}\right]\\
H_{zx,idx,idy}^{n+1/2} &= A_{sx}^*H_{zx,idx,idy}^{n-1/2}+C_{sx}^*\left[E_{y,idx+1,idy}^{n}-E_{y,idx,idy}^{n}\right]\\
H_{zy,idx,idy}^{n+1/2} &= A_{sy}^*H_{zy,idx,idy}^{n-1/2}-C_{sy}^*\left[E_{x,idx,idy+1}^{n}-E_{x,idx,idy}^{n}\right]
\end{align}
ただし
\begin{align}
A_{sw} &= \frac{\varepsilon_w}{\varepsilon_w+\sigma_w\Delta t}\\
B_{sw} &= \frac{\varepsilon_w\Delta t}{\varepsilon_w+\sigma_w\Delta t}\\
C_{sw} &= \frac{\Delta t}{d(\varepsilon_w+\sigma_w\Delta t)}
\end{align}
で、$w$方向に進行する電場の式に用いる係数です。$*$のついているのは各係数の誘電率と導電率を、透磁率と導磁率に入れ替えたモノです。ちなみに、磁流は存在しないので消しました。
解析フロー
解析フローを示します。
突貫工事で作ったのでこれが最適フローだとか一般的なフロートは言えません。各々工夫して可読性の高いものにしたり、高速なものにしたりしてください。個人的なポイントとしては、座標や電磁場の初期配列をまとめて作成するのではなく、座標を作ってからいったんPMLのサイズ設定をするところです。PML設定の時は解析空間が上下左右どれかに拡大するので配列サイズが変化します。最初に配列を初期化すると電磁場物性の配列に同じ操作を必要とするのでコードが長くなります。座標配列にだけこの操作をしてあとで同じサイズの電磁場と物性を作る方が楽です。
ループ中は特に工夫のしようがないと思います。それでは各ブロックごとにコードを書きます。と、その前に解析空間の端について考えます。
解析空間の端
上の式のうち、例えば
\begin{align}
E_{x,idx,idy}^{n+1} &= A_{sy}E_{x,idx,idy}^n-B_{sy}J_{0xy}+C_{sy}\left[H_{z,idx,jdy}^{n+1/2}-H_{z,idx,idy-1,k}^{n+1/2}\right]
\end{align}
を配列のイメージで考えた時、$H_{z,idx,jdy}^{n+1/2}-H_{z,idx,idy-1,k}^{n+1/2}$の部分は、画像処理の分野などでは畳み込みと呼ばれます。この畳み込みは対象配列から任意のマスずれた成分を足したり引いたりすることを言います。この処理はMATLABで言えば
Cn = E(:,2:end) - E(:,1:end-1);
などとかけますが、Cn(:,end)成分がどうなっているかは自分で追加しないと列数が減少してしまいます。
\begin{align}
E_{x,idx,idy}^{n+1} &= A_{sy}E_{x,idx,idy}^n-B_{sy}J_{0xy}+C_{sy}\left[H_{z,idx,jdy}^{n+1/2}-H_{z,idx,idy-1,k}^{n+1/2}\right]\\
E_{y,idx,idy}^{n+1} &= A_{sx}E_{y,idx,idy}^n-B_{sx}J_{0yx}-C_{sx}\left[H_{z,idx,idy}^{n+1/2}-H_{z,idx-1,idy}^{n+1/2}\right]\\
H_{zx,idx,idy}^{n+1/2} &= A_{sx}^*H_{zx,idx,idy}^{n-1/2}+C_{sx}^*\left[E_{y,idx+1,idy}^{n}-E_{y,idx,idy}^{n}\right]\\
H_{zy,idx,idy}^{n+1/2} &= A_{sy}^*H_{zy,idx,idy}^{n-1/2}-C_{sy}^*\left[E_{x,idx,idy+1}^{n}-E_{x,idx,idy}^{n}\right]
\end{align}
ExはHz(idx,idy)とHz(idx,idy-1)の差分なのでidy = 1の時にHz(idx,0)が枯渇します。MATLABはこれを自動で処理しないので、Ex(idx,1) = ~~~ Csy*Hz(idx,1)を追加しないといけません。同じことを電磁場全てやります。
設定値入力
ここではユーザが任意で設定できる定数を設定します。ひとまず以下を設定します。波源設定によっては周波数なども設定した方がいいでしょう。
% 解析空間サイズ
xSize = 50e-3;
ySize = 50e-3;
% セルの一辺
d = 4e-3/20;
% 解析終了時間
tend = 3e-10;
% 境界条件(0:PEC, 1:PMC, 2:PML)
% 右の壁
RWall = 2;
% 左の壁
LWall = 2;
% 上の壁
UWall = 2;
% 下の壁
FWall = 2;
解析空間の設定
解析空間はxサイズとyサイズを指定。セルのサイズは波長/10以下が経験的にいいです。ちなみに今回は全部メートルで記述します。物性の設定には一般的に比誘電率と比透磁率を使うので、真空(空気)の誘電率と透磁率もここで決めておきます。
% 光速
c = 2.99792458e8;
% 時間ステップ
dt = d/c/sqrt(2);
% 空気の誘電率と透磁率
AirEps = 8.8541878128e-12;
AirMu = 1.25663706212e-6;
% 座標(セルの中心)
[xPos, yPos] = meshgrid(-xSize/2-d/2:d:xSize/2+d/2,-ySize/2-d/2:d:ySize/2+d/2);
PMLの設定
PMLの分だけ解析空間を拡大します。元の配列に付け足すだけですね。
よくよく考えたらこの辺のパラメータも最初に書くべきでした。。。
% PMLの定数
thickPML = 8e-3;
depthPML = 0:d:thickPML;
Lami = length(depthPML);
% まずは解析空間の外側にPMLの層を確保
if RWall == 2
xPos = [xPos, repmat((1:Lami)*d + xSize/2 + d/2, size(xPos, 1), 1)];
yPos = [yPos, yPos(:,end).*ones(1,Lami)];
end
if LWall == 2
xPos = [repmat((-Lami:-1)*d - xSize/2 - d/2, size(xPos, 1), 1), xPos];
yPos = [yPos(:,1).*ones(1,Lami), yPos];
end
if UWall == 2
yPos = [yPos; repmat((1:Lami)'*d + ySize/2 + d/2, 1, size(yPos, 2))];
xPos = [xPos; xPos(end,:).*ones(Lami,1)];
end
if FWall == 2
yPos = [repmat((-Lami:-1)'*d - ySize/2 - d/2, 1, size(yPos, 2)); yPos];
xPos = [xPos(1,:).*ones(Lami,1); xPos];
end
電場磁場物性の初期値設定
PMLで拡大された座標配列と同じサイズで電場磁場物性の配列を作成します。それだけ。
% 電場
xEPre = zeros(size(xPos));
xENow = xEPre;
yEPre = xEPre;
yENow = xEPre;
% 電流密度
xJ = xEPre;
yJ = xEPre;
% 磁場
zxHPre = xEPre;
zxHNow = xEPre;
zyHPre = xEPre;
zyHNow = xEPre;
zHPre = xEPre;
zHNow = xEPre;
% 比誘電率
xEps = xEPre + 1;
yEps = xEPre + 1;
% 比透磁率
xMu = xEPre + 1;
yMu = xEPre + 1;
% 導電率
xSig = xEPre;
ySig = xEPre;
% 導磁率
xSigM = xEPre;
ySigM = xEPre;
物性入力
ここで物体が存在する座標の誘電率や透磁率などを書き換えます。円を設置する際はこんな感じ。
ep = 3;
r = 8e-3;
xCen = 0;
yCen = 0;
idCirc = (xPos-xCen).^2 + (yPos-yCen).^2 <= r^2;
yEps(idCirc) = ep;
xEps(idCirc) = ep;
PMLの物性割当て
序盤に作成したPML層に物性を当てはめます。具体的な式は前回記事を参照ください。書き換える値は導電率と導磁率で、反射率と乗数から求めます。
% 乗数
MPML = 4;
% 反射率
Rmax = 10e-10;
% 導電率の最大値
sigMAX = -(MPML+1)*sqrt(AirEps/AirMu)/2/Lami/d*log(Rmax);
% 導電率
sigPML = sigMAX*(depthPML/Lami/d).^MPML;
% 導磁率
sigMPML = sigPML*(AirMu/AirEps);
if RWall == 2
xSig(:,end-Lami+1:end) = ones(size(xSig,1),1).*sigPML;
xSigM(:,end-Lami+1:end) = ones(size(xSigM,1),1).*sigMPML;
end
if LWall == 2
xSig(:,1:Lami) = ones(size(xSig,1),1).*fliplr(sigPML);
xSigM(:,1:Lami) = ones(size(xSigM,1),1).*fliplr(sigMPML);
end
if UWall == 2
ySig(end-Lami+1:end,:) = ones(1,size(ySig,2)).*sigPML';
ySigM(end-Lami+1:end,:) = ones(1,size(ySigM,2)).*sigMPML';
end
if FWall == 2
ySig(1:Lami,:) = ones(1,size(ySig,2)).*flipud(sigPML');
ySigM(1:Lami,:) = ones(1,size(ySigM,2)).*flipud(sigMPML');
end
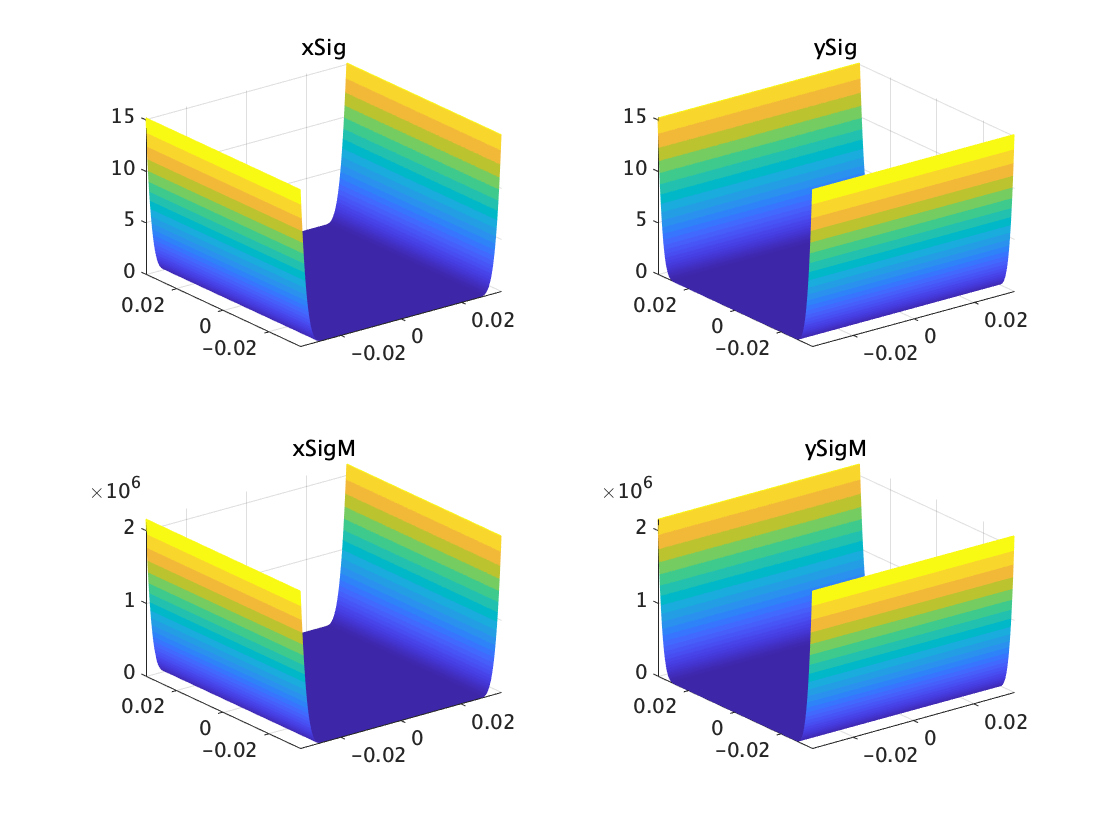
空間の四方をPMLにすると導電率と導磁率はこんな分布になります。
各種係数設定
ここでは記事冒頭の式に登場するA,B,Cを設定するだけです。
波源設定
波源は任意に設定してください。特にポイントはありません。波源位置をメートルから座標のインデックスに変換するなどの作業が必要ですが、roundとか使えばできます。
ループ
ループ内では波源の更新、電場計算、PEC壁の処理、磁場計算、PMC壁の処理を順番に繰り返します。式を間違えなければ特に問題ないはず。
これで基本的な処理は完成です。
fig = figure;
imag = imagesc(xPos(1,:),yPos(:,1)',zHNow);
caxis([-1e-7 1e-7])
axis equal
axis tight
hold on
colormap jet
t = 0:dt:tend;
for ic = 1:length(t)
% 波源設定 電界か電流密度を入力
xJ = sig(ic);
yJ = 0;
xJE = zeros(size(xENow));
xJE(yEmitIdx, xEmitIdx) = xJ;
yJE = zeros(size(yENow));
yJE(yEmitIdx, xEmitIdx) = yJ;
% ENowを計算
xENow = AEy.*xEPre - BEy.*xJE - CEy.*...
[zHNow(1,:); (zHNow(2:end,:)-zHNow(1:end-1,:))];
yENow = AEx.*yEPre - BEx.*yJE + CEx.*...
[zHNow(:,1), (zHNow(:,2:end)-zHNow(:,1:end-1))];
% 外周がPECの時
if RWall == 0
yENow(:,end) = 0;
end
if LWall == 0
yENow(:,1) = 0;
end
if UWall == 0
xENow(1,:) = 0;
end
if FWall == 0
xENow(end,:) = 0;
end
% HNowを計算
zxHNow = AHx.*zxHPre + CHx.*...
[yENow(:,2:end)-yENow(:,1:end-1), yENow(:,end)];
zyHNow = AHy.*zyHPre - CHy.*...
[xENow(2:end,:)-xENow(1:end-1,:); xENow(end,:)];
% 外周がPMCの時
if RWall == 1
zxHNow(:,end) = 0;
zyHNow(:,end) = 0;
end
if LWall == 1
zxHNow(:,1) = 0;
zyHNow(:,1) = 0;
end
if UWall == 1
zxHNow(1,:) = 0;
zyHNow(1,:) = 0;
end
if FWall == 1
zxHNow(end,:) = 0;
zyHNow(end,:) = 0;
end
zHNow = zxHNow + zyHNow;
% EPreにENowを格納
xEPre = xENow;
yEPre = yENow;
% HPreにHNowを格納
zxHPre = zxHNow;
zyHPre = zyHNow;
zHPre = zHNow;
% 描画
imag.CData = zHNow;
drawnow
end
まずは伝搬チェック
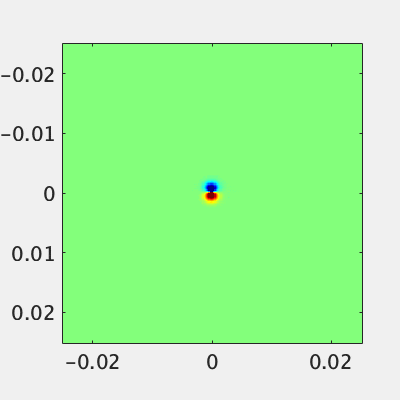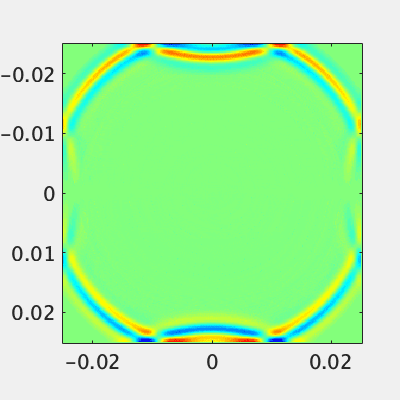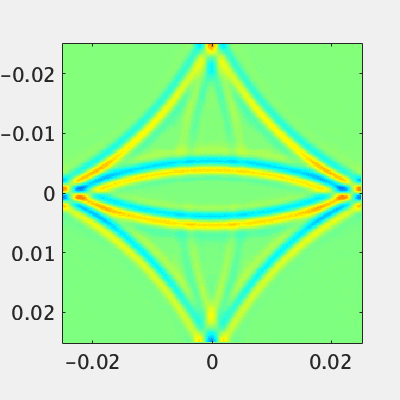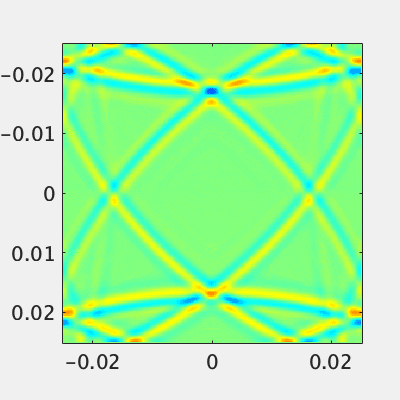
とりあえず外周をPECで囲った空間の中心にx方向の印加電流$J_{0x}$を配置してマザーウェーブレットを打ってみます。
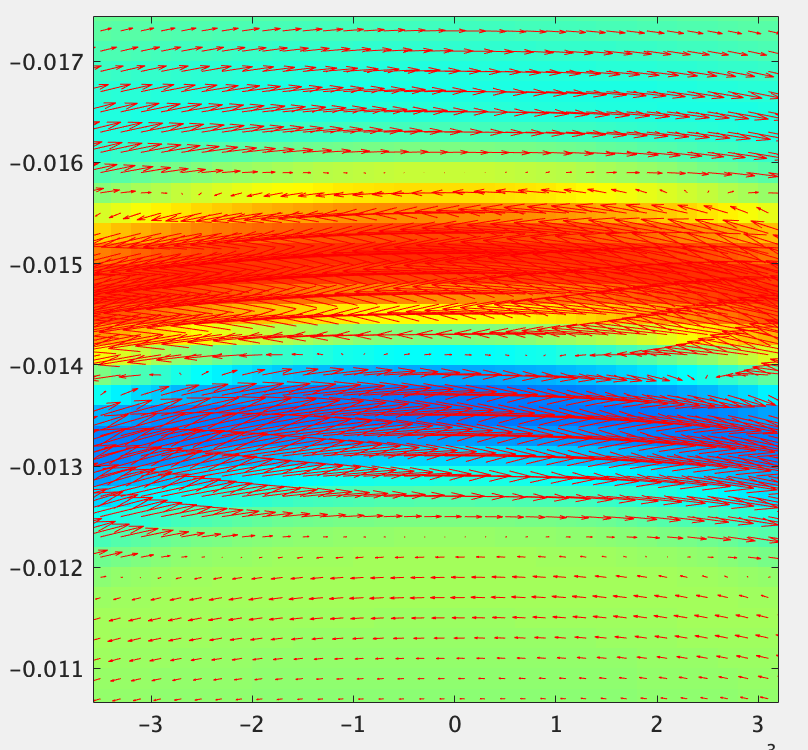
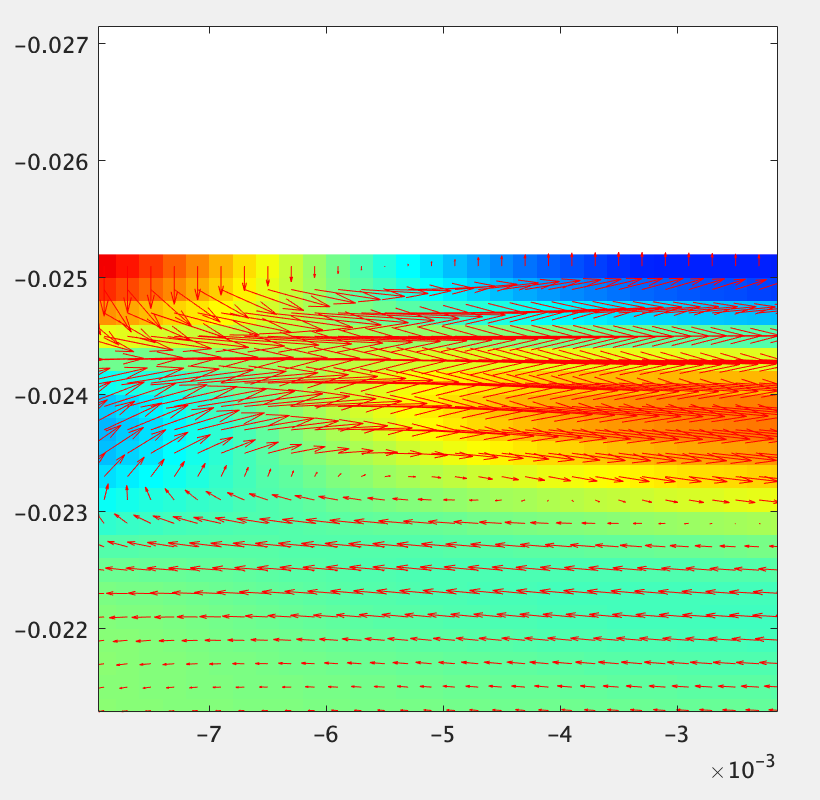
磁場のz成分を表示しています。x方向に電流が流れているのでポインティングの定理から、磁場は上下に逆相で放射されます。電場をベクトルで表示して画像上方向に伝搬する部分を観察すると、ちゃんとポインティングの定理を満たしていることがわかります。
PEC壁際を観察すると、電場は壁に対して垂直になっており、PECとして機能していることがわかります。
材料を入れよう
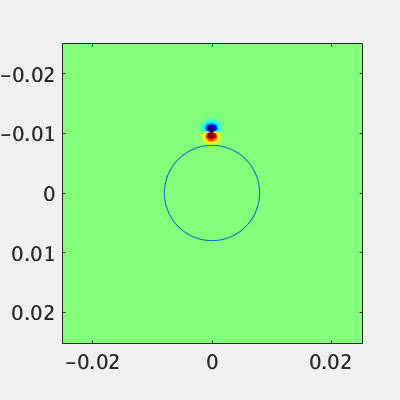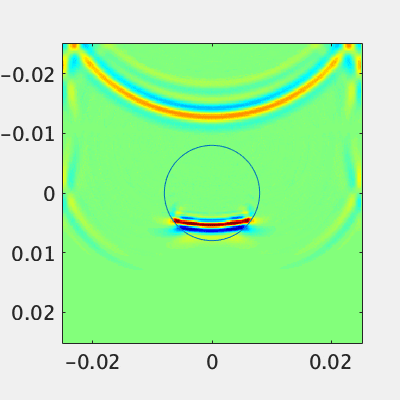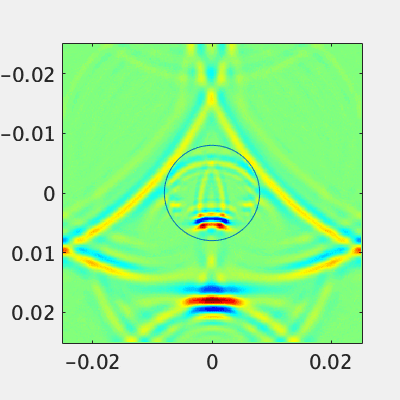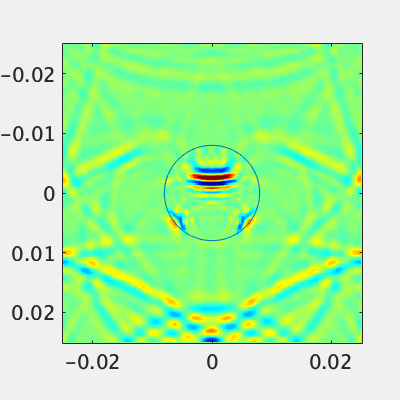
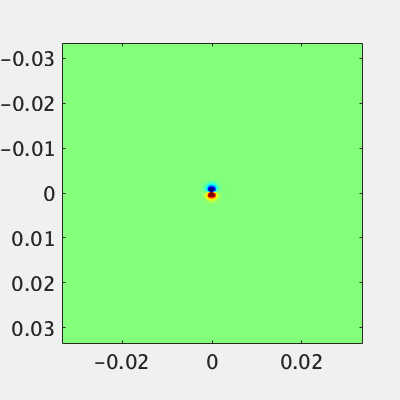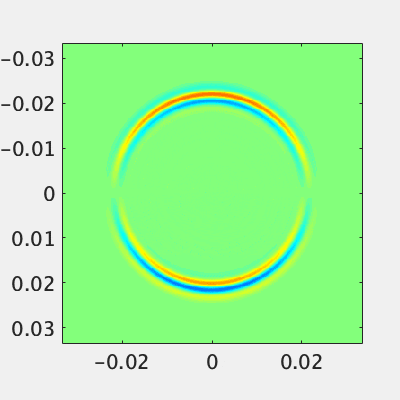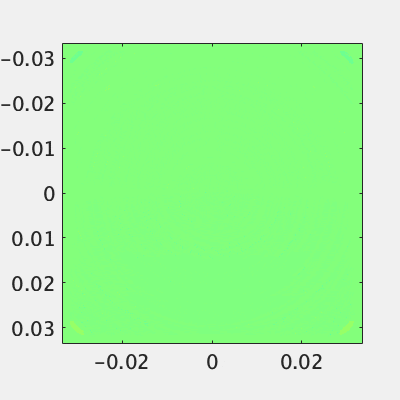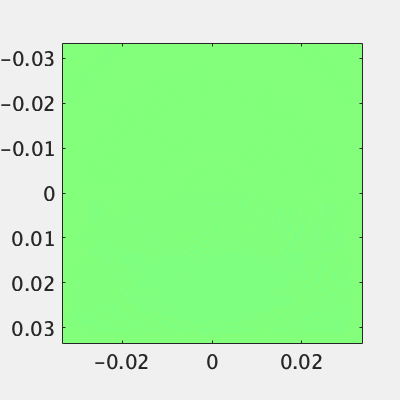
材料を入れる場合は誘電率などの配列に物性を入れるだけです。円状の誘電体を入れて見ましょう。
比誘電率3.0の材料を設置しました。一部の電力は誘電体内部へ、残りの電力は反射しています。
PECを入れよう
材料としてPECを入れる場合はその部分の電場をゼロに固定するだけで良いです。(PECは導電率と誘電率無限大の物質なので)
ちゃんと板の裏への回折も計算できてますね!
境界条件としてPECを使う場合は、上で説明した通り電場の接線成分をゼロにすることで実現できますが、面倒なので電場ゼロで再現しちゃった方が楽かも。
PMLを入れよう
PMLは解析空間の側壁に異方性の導電率と導磁率を設定します。前回記事の式に従って導電率と導磁率の勾配をつけます。
上図では周囲$2\lambda$の厚さのPMLを設定しています。少々難しいですがFDTDをやるにあたっては必須項目なので、自作しなくても理解しとくと良いと思います。
何か作ってみる
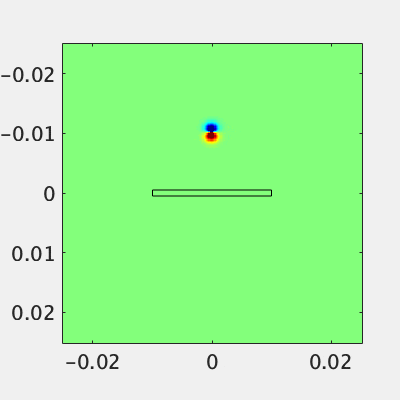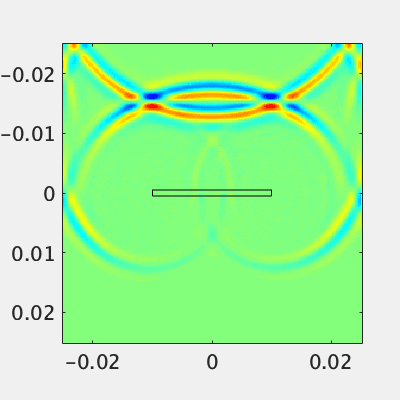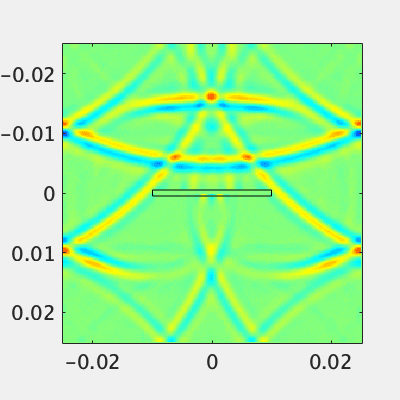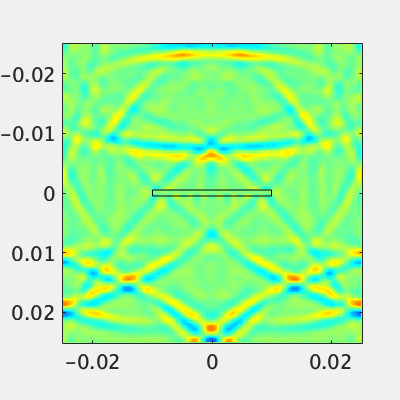
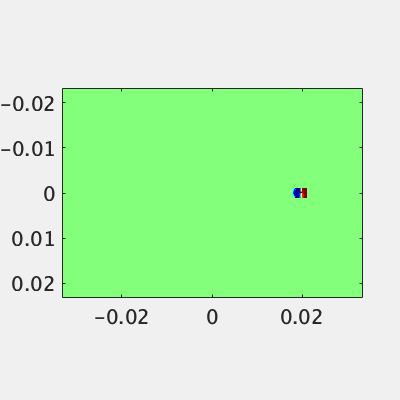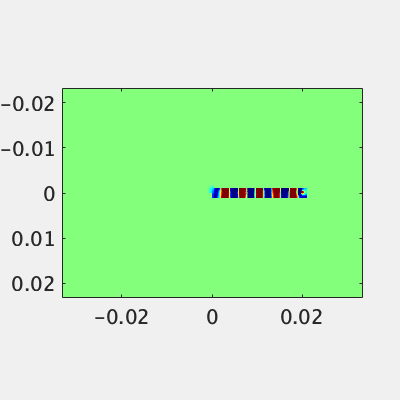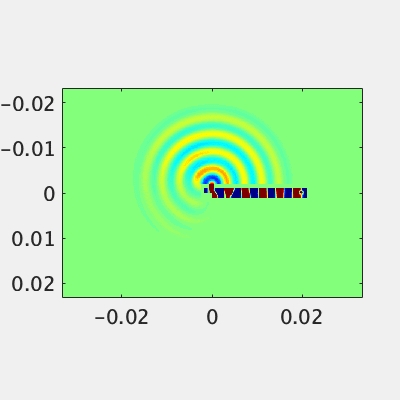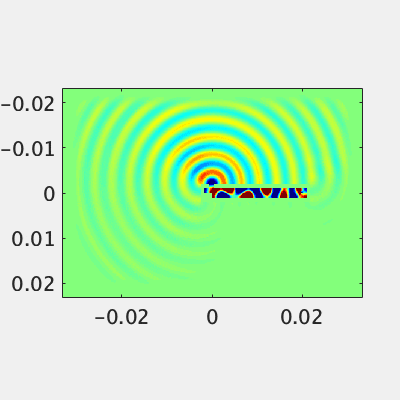
平板導波管からの放射
アンテナ設計者として基本的な導波管からの放射をやってみましょう。適当に平行平板を作って、中に電場を発生させます。平板の一部に隙間を開けて、反対側にインピーダンス調整用の出っ張りをつけます(完全なマッチングは無理)。スリットから終端までの距離はセオリーに則って$\lambda/4$とします。平板導波路なので管内波長は空気と同じです。
ローパスフィルタ
電磁波でローパスフィルタとはなんぞやという感じですが、いわゆるメタマテリアルの基本です。PECでできた平面状の周期構造に対して垂直に平面波を入力すると、特定周波数だけを狙って透過させたり反射させたりできます。無限周期構造の解析なので横の壁はPECとします。
まず低い周波数を入力
周波数が高いと
gifだとわかりにくいですが、高周波の方はフィルタ前により大きい定在波ができています。すなわち高周波ほど反射しているローパスフィルタというわけです。
まとめ
3回に渡って電磁界のFDTDを作成してきました。コードも基本的なものなので、シーンによってはバグりますが理論理解という意味では参考くらいにはなるかと思います。
電磁波を扱うような方々は、一度自分の手でコーディングしてみると解析だけでなく電磁波そのものの理解にもつながると思います。