Qiita界隈の方々はあまり電磁気学の世界の人がいなくて需要があるのかわかりませんが、@eigsさんにFDTDの記事を書いてほしいと言われてしまったのでがんばって書きます。MATLABerの方々のLGTMが20件くらいはくるかな??笑
FDTDとは
FDTDはWikipediaではこんな説明です。
FDTD法(Finite-difference time-domain method; FDTD method)は、数値計算の手法の1つ。日本語訳として「時間領域差分法」「有限差分時間領域法」などの呼び方もあるが、もっぱらFDTD法と呼ばれる。
「もっぱら」にクスッとしてしまいます。超ざっくり説明すると、時間と空間を離散化する解析手法です。Wikipediaの説明の通り電磁界解析でよく使われますが、別に力学解析でも使えると思います。
しかし、特に電磁界のFDTDは煩雑そうに見えるので専門家でもよく知らない人が多い、、、と勝手に思っています。
電磁界はマクスウェル方程式に支配されるので、まずはその理解から!
マクスウェル方程式
マクスウェル方程式は、マクスウェルさんがいろんな人が汗水たらしてやっとこさ発見した4つの方程式を、「これが電磁気の支配方程式や!」と言ってまとめただけの方程式です。一応式を書いておくと、
{\rm div} \boldsymbol{E} = \frac{\rho}{\varepsilon}\\
{\rm div} \boldsymbol{H} = 0\\
{\rm rot} \boldsymbol{H} = \boldsymbol{J}+\varepsilon\frac{\partial\boldsymbol{E}}{\partial t}\\
{\rm rot} \boldsymbol{E} = -\mu\frac{\partial\boldsymbol{H}}{\partial t}
上の式は、マクロなマクスウェル方程式と呼ばれ、$B = \mu H, D = \varepsilon E$としています。$\rho$は電荷密度、$\varepsilon$は誘電率、$J$は変位電流、$\mu$は透磁率、$\boldsymbol{E}$と$\boldsymbol{H}$は言わずもがな電界と磁界です。上から順にイメージを説明すると、
- 電荷密度(電荷)があると電場が発生する。電荷密度が一定なら電場の湧き出し量も一定。
- 磁場は湧き出さない。
- ある点の周囲で電場の変動があると磁場が発生する。(変位電流もね)
- ある点の周囲で磁場の変動があると電場が発生する。
1と2は湧き出しに関する方程式なので、FDTDには直接関係ありません。大事なのは3と4です。そういうわけで3と4を注目してみてみると、「電場が変動したら磁場が変動して、磁場が変動すると周囲に電場が発生して、電場が発生するとそのまた周囲で磁場が発生して。。。」と無限ループになります。これが電磁波が空間を伝搬する仕組みです。
回転形の方程式を図で理解しよう。
FDTDにはまだいきません。rotの説明をします。rotは$\nabla$と対象ベクトルの外積で以下のように表すことができます。
{\rm rot} \boldsymbol{v} = \nabla\times\boldsymbol{v} =
\left|
\begin{matrix}
\boldsymbol{i}&\boldsymbol{j}&\boldsymbol{k}\\
\frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\
v_x&v_y&v_z
\end{matrix}
\right|\\
=\left(\frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z}\right)\boldsymbol{i}+\left(\frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x}\right)\boldsymbol{j}+\left(\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\right)\boldsymbol{k}
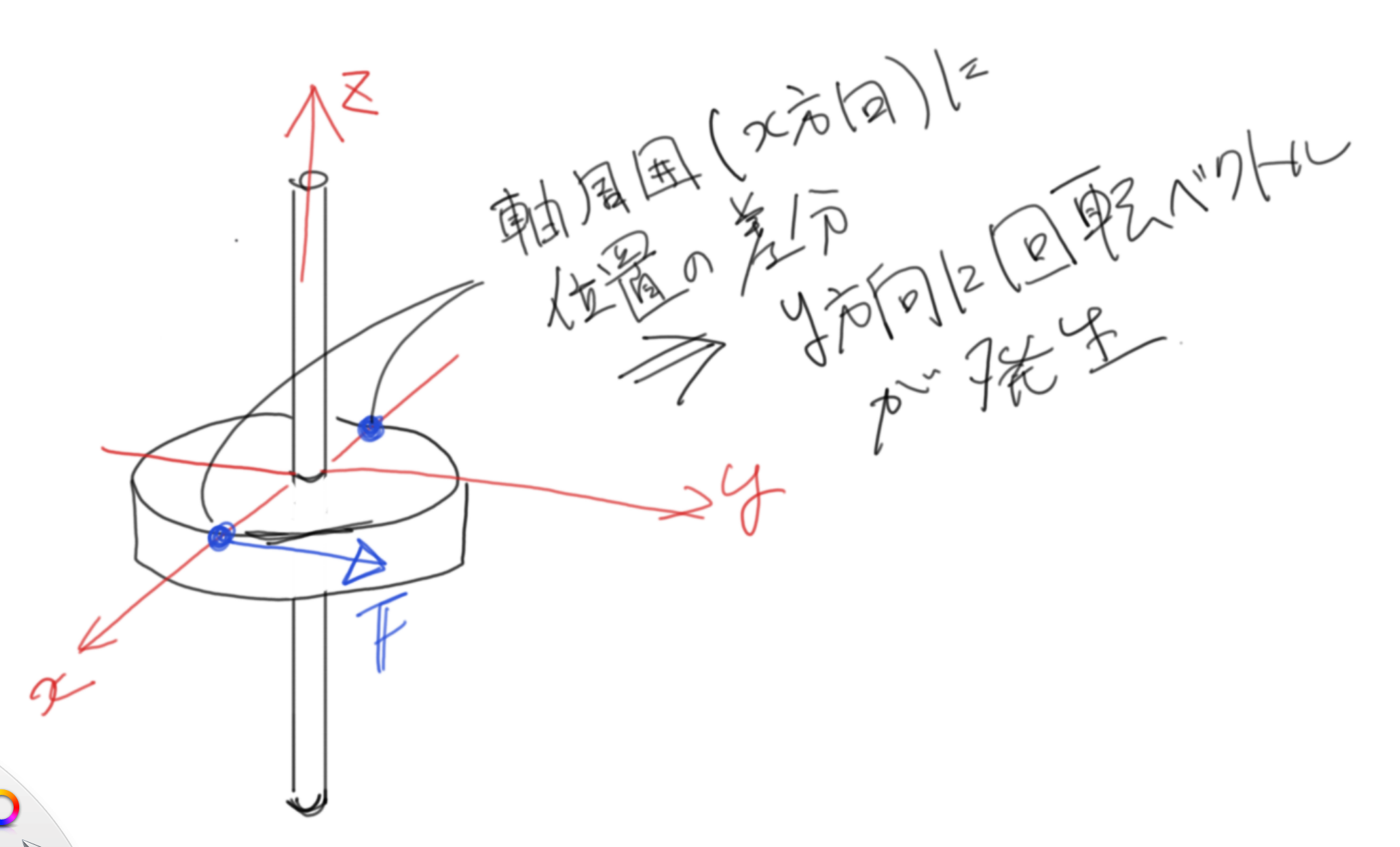
が、FDTDの理解に重要なのは問題はこれが何を表しているかです。そもそもrotは「ベクトル場の回転」を表す量で、コマをイメージするといいです。
コマの支柱を固定して、$\boldsymbol{v}=(v_x,v_y,v_z)$の成分のうち、$v_z$を支柱としましょう。円板部分の一点$\boldsymbol{v}(dx,0,0)$だけを回転方向に動かすと、力点の反対側と位置の差分が生まれて当然コマは回転しようとします。このとき、支柱はz方向なのでz方向に力を加えたり、$\boldsymbol{v}(dx,0,0)$においてx方向に力を与えても回転しません。
この回転量を数式で表したのがrotです。円板の直径の端を持ってそれぞれ回転方向に動かすと、先ほどよりも大きな位置の差分が生まれて強い回転量になります。
このように位置の差分$\partial \boldsymbol{v}/\partial y,\partial \boldsymbol{v}/\partial x$が回転量を表すことになり、回転の方向は別にどう決めてもいいのですが、右ねじの方向に従って定義されます。そして$v_z$に対する回転方向の力点はx,yの位置にあるので、$\boldsymbol{v}$のz方向に対するrotは、
\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}
になります。これをx方向,y方向に対して一般化すると$\nabla$との外積になります。
FDTDの原理
やっとFDTDの原理に入ります。最初に説明した通り「位置と時間の離散化」をすればいいので、偏微分の項を微小な位置や時間の差で表せば良いのです。
まずはシンプルな第四式を離散化します。$\Delta t$秒後の磁場の状態を求めたいので、
{\rm rot} \boldsymbol{E} = -\mu\frac{\partial\boldsymbol{H}}{\partial t}\\
\Rightarrow \nabla\times\boldsymbol{E} = -\mu\frac{\partial\boldsymbol{H}}{\partial t}\\
\Rightarrow \left(\frac{\partial E_z}{\partial y}-\frac{\partial E_y}{\partial z}\right)\boldsymbol{i}+\left(\frac{\partial E_x}{\partial z}-\frac{\partial E_z}{\partial x}\right)\boldsymbol{j}+\left(\frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y}\right)\boldsymbol{k}
= -\mu \frac{\boldsymbol{H}(t+\Delta t)-\boldsymbol{H}(t)}{\Delta t}\\
\Rightarrow \boldsymbol{H}(t+\Delta t) = \boldsymbol{H}(t)-\frac{\Delta t}{\mu}\left[\left(\frac{\partial E_z}{\partial y}-\frac{\partial E_y}{\partial z}\right)\boldsymbol{i}+\left(\frac{\partial E_x}{\partial z}-\frac{\partial E_z}{\partial x}\right)\boldsymbol{j}+\left(\frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y}\right)\boldsymbol{k}\right]
となります。時間の離散化はまあいいでしょう。単純に微小時間差で差分を取ればいいです。問題は位置の微分です。FDTDの基本は空間をブロック状に仕切り、各面の中心に電場や磁場をおき、rotをx,y,z成分に分けて計算します。
セルの辺の長さを$\Delta x,\Delta y,\Delta z$として、点(x,y,z)で回転をとると、面上の各点の各軸方向における差分をとってくるのと同義なので、例えば
\frac{\partial E_z}{\partial y}
この項の離散化した式は
\frac{\partial E_z}{\partial y} = \frac{E_z(x,y+\Delta y/2,z)-E_z(x,y-\Delta y/2,z)}{\Delta y}
となります。x成分に対するrotを計算すると、
\frac{\partial E_z}{\partial y}-\frac{\partial E_y}{\partial z}\\
= \frac{E_z(x,y+\Delta y/2,z)-E_z(x,y-\Delta y/2,z)}{\Delta y}-
\frac{E_y(x,y,z+\Delta z/2)-E_y(x,y,z-\Delta z/2)}{\Delta z}
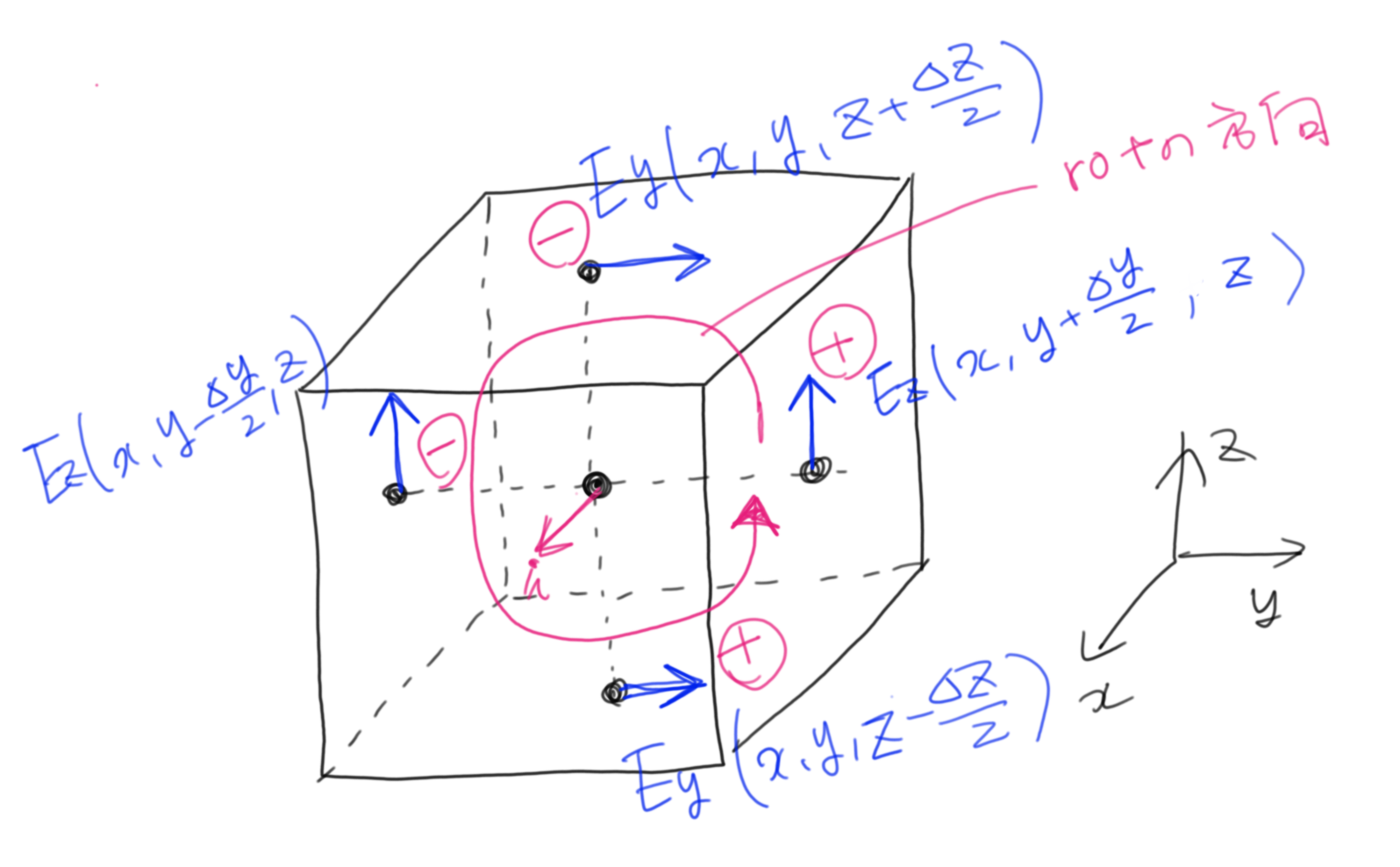
となります。この式について図を描いてみましょう。
回転をとるとき、正負がややこしくなると思います。上のrotの説明でもそうだったかもしれません。しかしFDTDのセルだと話は単純です。x方向の回転を取りたい場合、x方向に対して右ねじの方向に沿って±を付ければいいのです。すなわちこの場合は図中にあるように、回転方向に沿っている$E_z(x,y+\Delta y/2,z), E_y(x,y,z-\Delta z/2)$は正で、他の2つは負になります。微分ですので$\Delta z,\Delta y$で割ったりしてますが、セルで考えるとrot計算のイメージは簡単ですね。
そして第三式も同様に離散化できます。とりあえずこれで数式的な離散化の感覚は理解できたかと思います。
解析フロー
電磁界解析では電場と磁場を両方計算せねばらない上に、マクスウェルの式は磁場が求まると電場がもとまり、電場が求まると磁場が求まる形になっています。なので解析では電場か磁場に初期値を与え、時間ステップごとに電場と磁場を交互に計算します。
で、上で離散化したこの式を眺めてみてください。
\boldsymbol{H}(t+\Delta t) = \boldsymbol{H}(t)-\frac{\Delta t}{\mu}\left[\left(\frac{\partial E_z}{\partial y}-\frac{\partial E_y}{\partial z}\right)\boldsymbol{i}+\left(\frac{\partial E_x}{\partial z}-\frac{\partial E_z}{\partial x}\right)\boldsymbol{j}+\left(\frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y}\right)\boldsymbol{k}\right]
続けてセルの点の配置を眺めてください。
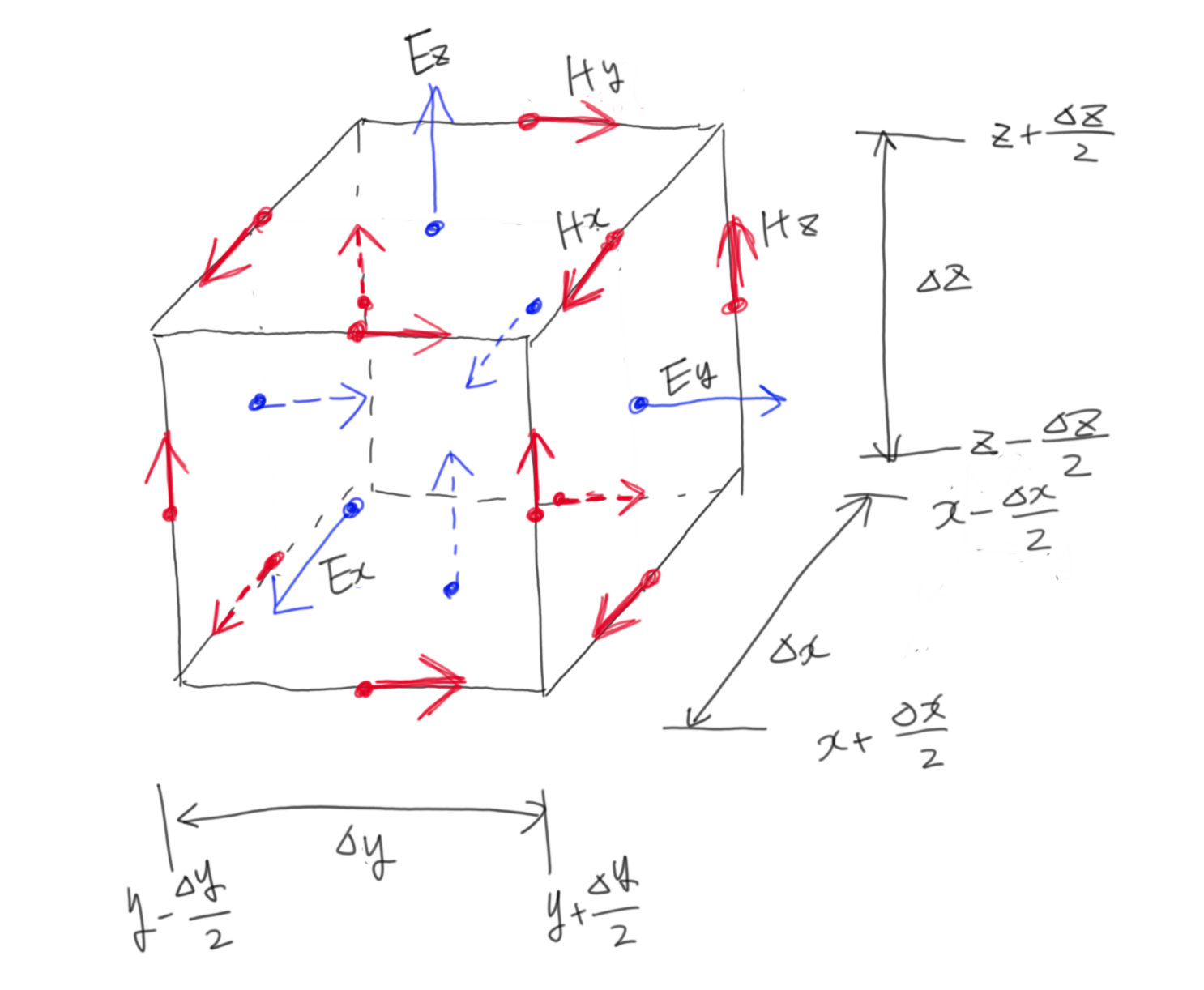
よくよく思い出してみると、セルの中心(x,y,z)の点での回転をとる式ですよね。電場の回転をとっているので、その結果は$\boldsymbol{H}(t+\Delta t)$になります。つまり、セルの面の中心である6点は電場であり、セルの重心は磁場なのです。これが電磁界のFDTDの面倒なところで、離散化した回転をとっているため電場と磁場の位置が違うんです。しかも、このままだと電場から見た磁場の座標の位置関係と、磁場から見た電場のそれは異なりますね。これではシステマティックに解けないので、Yeeセルと呼ばれるセルを導入します。
さあわけわかんなくなってきました。Yeeセルを簡単に説明すると、電場と磁場のx,y,z,各成分を、回転の取りやすいように再配置したものです。磁場は変に平行な成分を、電場は面に垂直な成分を配置しています。微小なセルであれば、各成分の位置が$\Delta x,\Delta y,\Delta z,$ずれていることは無視できます。各ベクトルは隣接するセルと共有されるため、その向きは軸方向に合わせておきます。上の方でrotをイメージで説明したのがここで生きてきます。偏微分方程式を離散化してこねこねしてたのも重要ですが、ここからはイメージでいきましょう。コマのイメージ通り、回転はあるベクトルの右ネジ方向に回転する成分の足し合わせです。例えば図中の$E_y(x,y+\Delta y/2,z)$を求める際、その周囲の$H$の回転が必要ですが、それは以下のように求められます。
{\rm rot} H|_{E_y(x,y+\Delta y/2,z)}=[H_z(x-\Delta x/2,y+\Delta y/2,z)-H_z(x+\Delta x/2,y+\Delta y/2,z)]/\Delta x\\
+[H_z(x,y+\Delta y/2,z+\Delta z/2)-H_z(x,y+\Delta y/2,z-\Delta z/2)]/\Delta z
右ねじ成分を向きに注意して足すだけですね。電磁場のベクトルの成分を分解して、その位置を少し寛容にしてやるだけで、回転が格段に取りやすくなりました。これでFDTDの難関はク・リ・ア・death!
時間について
お次、時間についてですが、FDTDでは電場と磁場を$\Delta t$おきに交互に計算するため、ある時間の電場を計算した後、次に電場が計算されるのは$2\Delta t$後になります。イメージ図は下の通り
$E(t)$--->$H(t+\Delta t)$--->$E(t+2\Delta t)$--->$\cdots$
これでもいいんですが、感覚的にもどかしいので電場と磁場を計算する際の時間ステップは$\Delta t/2$にすることが通常です。
ひとまずまとめ
ここまでで頭がいっぱいいっぱいかもしれませんが、ひとまず離散化された式をまとめます。元にするマクスウェル方程式はこれ
{\rm rot} \boldsymbol{H} = \boldsymbol{J}+\varepsilon\frac{\partial\boldsymbol{E}}{\partial t}\\
{\rm rot} \boldsymbol{E} = -\mu\frac{\partial\boldsymbol{H}}{\partial t}
そしてYeeセルを用いて離散化した磁場の式がこちら、時間ステップは$\Delta t/2$としています。Yeeセルの座標の基準は文献によって異なる場合があるので注意してください。そして書き間違っている可能性大ですので、ご自分で確認しながら使ってください。ミスの指摘も歓迎です。
\begin{align}
H_x(x,y+\Delta y/2,z+\Delta z/2,t+\Delta t/2) &= H_x(x,y+\Delta y/2,z+\Delta z/2,t-\Delta t/2)\\
&-\frac{\Delta t}{2\mu}\left[\frac{E_z(x,y+\Delta y,z+\Delta z/2,t)-E_z(x,y,z+\Delta z/2,t)}{\Delta y}\\
-\frac{E_y(x,y+\Delta y/2,z+\Delta z,t)-E_y(x,y+\Delta y/2,z,t)}{\Delta z}\right]\\
H_y(x+\Delta x/2,y,z+\Delta z/2,t+\Delta t/2) &= H_y(x+\Delta x/2,y,z+\Delta z/2,t-\Delta t/2)\\
&-\frac{\Delta t}{2\mu}\left[\frac{E_x(x+\Delta x/2,y,z+\Delta z,t)-E_x(x+\Delta x/2,y,z,t)}{\Delta z}\\
-\frac{E_z(x+\Delta x,y,z+\Delta z/2,t)-E_z(x,y,z+\Delta z/2,t)}{\Delta x}\right]\\
H_z(x+\Delta x/2,y+\Delta y/2,z,t+\Delta t/2) &= H_z(x+\Delta x/2,y+\Delta y/2,z,t-\Delta t/2)\\
&-\frac{\Delta t}{2\mu}\left[\frac{E_y(x+\Delta x,y+\Delta y/2,z,t)-E_y(x,y+\Delta y/2,z,t)}{\Delta x}\\
-\frac{E_x(x+\Delta x/2,y+\Delta y,z,t)-E_x(x+\Delta x/2,y,z,t)}{\Delta y}\right]
\end{align}
続いて電場の式がこちら、電場は先の$\boldsymbol{H}(t+\Delta t/2)$を用いて計算します。
\begin{align}
E_x(x+\Delta x/2,y,z,t+\Delta t) &= E_x(x+\Delta x/2,y,z,t)\\
&+\frac{\Delta t}{2\varepsilon}\left[\frac{H_z(x+\Delta x/2,y+\Delta y/2,z,t+\Delta t/2)-H_z(x+\Delta x/2,y-\Delta y/2,z,t+\Delta t/2)}{\Delta y}\\
-\frac{H_y(x+\Delta x/2,y,z+\Delta z/2,t+\Delta t/2)-H_y(x+\Delta x/2,y,z-\Delta z/2,t+\Delta t/2)}{\Delta z}-J_x(t)\right]\\
E_y(x,y+\Delta y/2,z,t+\Delta t) &= E_y(x,y+\Delta y/2,z,t)\\
&+\frac{\Delta t}{2\varepsilon}\left[\frac{H_x(x,y+\Delta y/2,z+\Delta z/2,t+\Delta t/2)-H_x(x,y+\Delta y/2,z-\Delta z/2,t+\Delta t/2)}{\Delta z}\\
-\frac{H_z(x+\Delta x/2,y+\Delta y/2,z,t+\Delta t/2)-H_z(x-\Delta x/2,y+\Delta y/2,z,t+\Delta t/2)}{\Delta x}-J_y(t)\right]\\
E_z(x,y,z+\Delta z/2,t+\Delta t) &= E_z(x,y,z+\Delta z/2,t)\\
&+\frac{\Delta t}{2\varepsilon}\left[\frac{H_y(x+\Delta x/2,y,z+\Delta z/2,t+\Delta t/2)-H_y(x-\Delta x/2,y,z-\Delta z/2,t+\Delta t/2)}{\Delta x}\\
-\frac{H_x(x,y+\Delta y/2,z+\Delta z/2,t+\Delta t/2)-H_x(x,y-\Delta y/2,z+\Delta z/2,t+\Delta t/2)}{\Delta y}-J_z(t)\right]
\end{align}
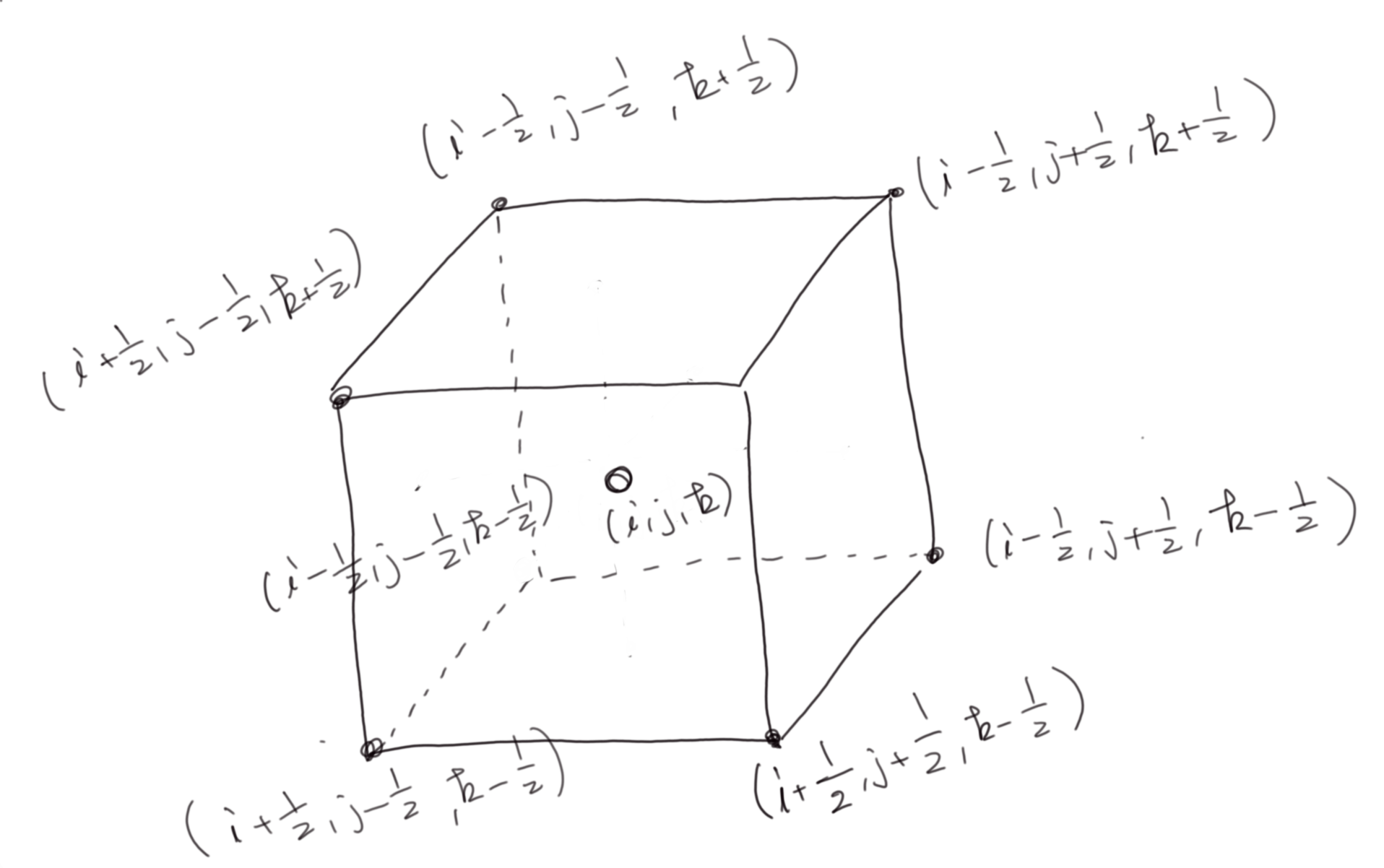
みるだけで目が痛くなるとはこのこと。安心してくださいこれから少しだけ見やすい式を提示します。セルは通常立方体とされ、その重心の座標を(x(i),y(j),z(k))とします。ベクトルのi,j,kと混同しないように!
セルの一辺の長さは$d$とし、時間も$t(n)$とします。このインデックス$i,j,k,n$で電場磁場をかくと、
\begin{align}
H_x(i,j+1/2,k+1/2,n+1/2) &= H_x(i,j+1/2,k+1/2,n-1/2)\\
&-\frac{\Delta t}{2d\mu}[E_z(i,j+1,k+1/2,n)-E_z(i,j,k+1/2,n)\\
&-E_y(i,j+1/2,k+1,n)+E_y(i,j+1/2,k,n)]\\
H_y(i+1/2,j,k+1/2,n+1/2) &= H_y(i+1/2,j,k+1/2,n-1/2)\\
&-\frac{\Delta t}{2d\mu}[E_x(i+1/2,j,k+1,n)-E_x(i+1/2,j,k,n)\\
&-E_z(i+1,j,k+1/2,n)+E_z(i,j,k+1/2,n)]\\
H_z(i+1/2,j+1/2,k,n+1/2) &= H_z(i+1/2,j+1/2,k,n-1/2)\\
&-\frac{\Delta t}{2d\mu}[E_y(i+1,j+1/2,k,n)-E_y(i,j+1/2,k,n)\\
&-E_x(i+1/2,j+1,k,n)+E_x(i+1/2,j,k,n)]
\end{align}
続いて電場を書き直すと。。。
\begin{align}
E_x(i+1/2,j,k,n+1) &= E_x(i+1/2,j,k,n)\\
&+\frac{\Delta t}{2d\varepsilon}[H_z(i+1/2,j+1/2,k,n+1/2)-H_z(i+1/2,j-1/2,k,n+1/2)\\
&-H_y(i+1/2,j,k+1/2,n+1/2)+H_y(i+1/2,j,k-1/2,n+1/2)-dJ_x(n)]\\
E_y(i,j+1/2,k,n+1) &= E_y(i,j+1/2,k,n)\\
&+\frac{\Delta t}{2d\varepsilon}[H_x(i+1/2,j+1/2,k,n+1/2)-H_x(i+1/2,j-1/2,k,n+1/2)\\
&-H_z(i+1/2,j,k+1/2,n+1/2)+H_z(i+1/2,j,k-1/2,n+1/2)-dJ_y(n)]\\
E_z(i,j,k+1/2,n+1) &= E_z(i,j,k+1/2,n)\\
&+\frac{\Delta t}{2d\varepsilon}[H_y(i+1/2,j,k+1/2,n+1/2)-H_y(i-1/2,j,k+1/2,n+1/2)\\
&-H_x(i,j+1/2,k+1/2,n+1/2)+H_x(i,j-1/2,k+1/2,n+1/2)-dJ_z(n)]
\end{align}
もう何処か書き間違えている気しかしません。
これらの式を、$\Delta t/2$ごとに電場->磁場->電場->磁場・・・と繰り返していくだけです。
セルの切り方
FDTDでは空間をセルに区切り、電場磁場の各軸成分を意図的に分散して配置することで、rot計算を簡単にしています。従って当然ですがセルは十分に細かい必要があります。かんばって実装する方のために安定化条件を示しておきます。
\Delta t \leq \left(v\sqrt{\Delta x^{-2}+\Delta y^{-2}+\Delta z^{-2}}\right)^{-1}
$v$は媒質中の光速度です。
まとめ
疲れたのでいったん区切ります。今回はFDTDの原理について一通りまとめました。次回は吸収境界条件の話か、実装の話ですかね。。。
余談ですが、電磁界解析には大きく分けて時間領域の解析と、周波数領域の解析があります。FDTDは時間領域の解析に分類され、入力する波は時間波形として入力します。時間領域解析のメリットは、周波数スペクトルの解析が速いことで、インパルスを入力してFFTすれば広帯域なスペクトルがすぐに見られます。
次回以降の記事はこちら
【FDTD解説シリーズ②】FDTDのもう一歩深くへ
【FDTD解説シリーズ③】電磁界FDTDを実装しよう