LSTMを使用した株価予測_1

『PyTorchニューラルネットワーク実装ハンドブック』の第5章RNNを読了したので、試しに株価分析してみました。

その備忘録です。

はじめに

トヨタ自動車(7203)の過去20年分の株価（始値、高値、安値、終値）から、翌日のリターン(翌日終値 - 翌日始値)が2-3.5%になるか否かを予測しました（2値分類問題）。

なぜ、2-3.5%なのかというと、1) 最低限のリターンを確保するため、2) ニュースなどによるファンダメンタル要因の株価変動を無視するためです。
また、以前TOPIX500の1日リターン（終値-始値）を分析したときに2-3.5%のリターンが5%前後であり、予測するのにちょうど良かったという経緯もあります。

レンジ	リターン(%)
～ -3.5	4.5
-3.5 ～ -0.5	7.4
-2.0 ～ -0.5	22.6
-0.5 ～ 0.5	34.5
0.5 ～ 2.0	19.5
2.0 ～ 3.5	6.5
3.5 ～	5.0

結果
過去75日分データを説明変数として予測したところ、正答率97.42%をマークしました（←怪しいので要検証）。

実装にあたっては、冒頭の書籍とこちらのサイトを参考にしました。
https://stackabuse.com/time-series-prediction-using-lstm-with-pytorch-in-python/

前準備

まずは必要なライブラリをimportします。

import torch
import torch.nn as nn
import torch.optim as optim

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

分析データがGoogleDrive上にあるので、以下のコードでドライブにアクセスできる状態にしておきます。

from google.colab import drive
drive.mount('/content/drive')

cudaを使用できるかチェックし、deviceの指定をしておきます。

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
device

データの読み込み

今回はトヨタ自動車(7203)の株価データ(1983年以降27年分のデータ)を使用します。

df_init = pd.read_csv('/content/drive/My Drive/XXXXXXXXXX/7203.csv', encoding='sjis')
df_init.head()

	銘柄コード	日付	始値	高値	安値	終値
0	7203	30320	747.911341	754.710535	741.112147	741.112147
1	7203	30321	747.911341	747.911341	720.714565	734.312953
2	7203	30322	720.714565	727.513759	707.116177	713.915371
3	7203	30323	727.513759	734.312953	713.915371	727.513759
4	7203	30324	727.513759	727.513759	720.714565	727.513759

あまり変数が多くても、1) 計算時間が長いなる、2) 過学習のおそれがあるため、今回は変数を始値、高値、安値、終値だけに絞って分析を行うことにします。

df = pd.DataFrame()
df['open'] = df_init['始値']
df['high'] = df_init['高値']
df['low'] = df_init['安値']
df['close'] = df_init['終値']
# 翌日リターン(終値-始値)を計算し、2-3.5%のときにフラグを1にする。
df['return'] = (df_init['終値'].shift() - df_init['始値'].shift())/df_init['始値'].shift()
df['return'] = ((df['return']>=0.02) & (df['return']<=0.035)).astype(int)
print(len(df))
print(sum(df['return']))
df.head()

時系列分析のためのデータを作成する。今回は過去75日分(≓3ヶ月)のデータを説明変数として使用します。

window = 75

def create_inout_sequences(in_data, in_label, window):
    out_seq = []
    out_label = [] 
    length = len(in_data)
    for i in range(window, length):
        tmp_data = in_data[i-window:i+1] / in_data[i,3]
        tmp_label = [in_label[i]]
        out_seq.append(torch.Tensor(tmp_data))
        out_label.append(torch.Tensor(tmp_label).type(torch.long))
    return out_seq, out_label

out_seq, out_label = create_inout_sequences(df.iloc[:,:4].values, df.iloc[:,4].values, window)

データを出力して、目的のデータとなっているか確認します。

print(len(out_seq))
print(out_seq[0])
print(out_label[0])

''' 出力
8660
tensor([[1.0577, 1.0673, 1.0481, 1.0481],
        [1.0577, 1.0577, 1.0192, 1.0385],
        [1.0192, 1.0288, 1.0000, 1.0096],
        [1.0288, 1.0385, 1.0096, 1.0288],
        [1.0288, 1.0288, 1.0192, 1.0288],
             ～～　省略　～～       
        [1.0288, 1.0385, 1.0288, 1.0385],
        [1.0288, 1.0385, 1.0192, 1.0192],
        [1.0192, 1.0288, 1.0000, 1.0000],
        [1.0096, 1.0192, 1.0000, 1.0192],
        [1.0192, 1.0288, 1.0000, 1.0000]])
tensor([0])
'''

データを、訓練用、評価用、推論用に分けます。
それぞれのデータ数は適当です。それぞれのデータが重ならないよう各データ間は100日分(>75日)のインターバルを設けています。

x_train = out_seq[:5000]
x_valid = out_seq[5100:6000]
x_test = out_seq[6100:]
y_train = out_label[:5000]
y_valid = out_label[5100:6000]
y_test = out_label[6100:]

モデル作成

入力→LSTM→全結合層からなるモデルを構築します。2値分類なので、出力次元は"2"です。
今回は試しなので、バッチや隠れ層のサイズに深い意味はありません。

input_size=4
batch_size = 32
hidden_layer_size=50
output_size=2

class LstmClassifier(nn.Module):
    def __init__(self, input_size, hidden_layer_size, output_size, batch_size):
        super().__init__()
        self.batch_size = batch_size
        self.hidden_layer_size = hidden_layer_size
        # lstmはデフォルトでbatch_first=Falseなので、batch_first=Trueにする
        self.lstm = nn.LSTM(input_size, hidden_layer_size, batch_first=True)
        self.fc = nn.Linear(hidden_layer_size, output_size)
        self.softmax = nn.Softmax(dim=1)
        # 初期隠れ状態とセル状態を設定
        self.hidden_cell = (torch.zeros(1, self.batch_size, self.hidden_layer_size).to(device),
                            torch.zeros(1, self.batch_size, self.hidden_layer_size).to(device))

    def forward(self, input_seq):
        x = input_seq
        # LSTMを伝播する
        lstm_out, self.hidden_cell = self.lstm(x, self.hidden_cell)
        out = self.fc(self.hidden_cell[0])
        out = out[-1]
        return out


model = LstmClassifier(input_size, hidden_layer_size, output_size, batch_size)
model = model.to(device)
model

''' 出力
LstmClassifier(
  (lstm): LSTM(4, 50, batch_first=True)
  (fc): Linear(in_features=50, out_features=2, bias=True)
  (softmax): Softmax(dim=1)
)
'''

損失関数に交差エントロピー、最適化関数にAdamを使用します。

criterion = nn.CrossEntropyLoss()
optimiser = optim.Adam(model.parameters())

学習

とりあえずエポック数を100として学習を実施してみます。

エポック毎にdetachで勾配を打ち切っていますが、RNNは計算量が多いのでメモリ使用量の削減のために不要となった中間結果をdetachで削除しているようです（参考）。

num_epochs = 100
train_loss_list = []
train_acc_list = []
val_loss_list = []
val_acc_list = []

# 逆伝播を途中で打ち切る
def detach(states):
    return [state.detach() for state in states] 

# Tensorを結合
def cat_Tensor(data, i_batch, batch_size):
    for i, idx in enumerate(range(i_batch*batch_size, (i_batch+1)*batch_size)):
        # 次元を増やす
        tmp = torch.unsqueeze(data[idx], 0)
        if i==0:
            output = tmp
        else:
            output = torch.cat((output, tmp), 0)
    return output

for i_epoch in range(num_epochs):

    train_loss = 0
    train_acc = 0
    val_loss = 0
    val_acc = 0

    #train
    model.train()

    n_batch = len(x_train)//batch_size
    for i_batch in range(n_batch):
        seq = cat_Tensor(x_train, i_batch, batch_size)
        labels = cat_Tensor(y_train, i_batch, batch_size)
        labels = torch.squeeze(labels, 1)

        seq = seq.to(device)
        labels = labels.to(device)
        
        # 勾配をリセット
        optimiser.zero_grad()
        # 逆伝播を途中で打ち切る。Error対策
        model.hidden_cell = detach(model.hidden_cell)
        # 順伝播
        outputs = model(seq)
        # 誤差逆伝播
        loss = criterion(outputs, labels)
        # 誤差の蓄積
        train_loss += loss.item()
        train_acc += (outputs.max(1)[1] == labels).sum().item()
        # 逆伝播の計算
        loss.backward()
        # 重みの更新
        optimiser.step()

    avg_train_loss = train_loss / n_batch
    avg_train_acc = train_acc / (n_batch*batch_size)

    #val
    model.eval()
    with torch.no_grad():
        n_batch = len(x_valid)//batch_size
        for i_batch in range(n_batch):
            seq = cat_Tensor(x_valid, i_batch, batch_size)
            labels = cat_Tensor(y_valid, i_batch, batch_size)
            labels = torch.squeeze(labels, 1)

            seq = seq.to(device)
            labels = labels.to(device)

            # 順伝播
            outputs = model(seq)
            loss = criterion(outputs, labels)
            # 誤差の蓄積
            val_loss += loss.item()
            val_acc += (outputs.max(1)[1] == labels).sum().item()

    avg_val_loss = val_loss / n_batch
    avg_val_acc = val_acc / (n_batch*batch_size)
    
    print ('Epoch [{}/{}], Loss: {loss:.4f}, val_loss: {val_loss:.4f}, Acc:{acc:.4f}, val_acc: {val_acc:.4f}' 
        .format(i_epoch+1, num_epochs, loss=avg_train_loss, val_loss=avg_val_loss, 
                acc=avg_train_acc, val_acc=avg_val_acc))
    
    train_loss_list.append(avg_train_loss)
    train_acc_list.append(avg_train_acc)
    val_loss_list.append(avg_val_loss)
    val_acc_list.append(avg_val_acc)


''' 出力
Epoch [1/100], Loss: 0.1198, val_loss: 0.0632, Acc:0.9439, val_acc: 0.9743
Epoch [2/100], Loss: 0.1147, val_loss: 0.0609, Acc:0.9397, val_acc: 0.9743
Epoch [3/100], Loss: 0.1119, val_loss: 0.0590, Acc:0.9403, val_acc: 0.9743
Epoch [4/100], Loss: 0.1096, val_loss: 0.0569, Acc:0.9407, val_acc: 0.9743
Epoch [5/100], Loss: 0.1069, val_loss: 0.0557, Acc:0.9417, val_acc: 0.9754
Epoch [6/100], Loss: 0.1046, val_loss: 0.0544, Acc:0.9437, val_acc: 0.9754
Epoch [7/100], Loss: 0.1032, val_loss: 0.0525, Acc:0.9455, val_acc: 0.9799
Epoch [8/100], Loss: 0.1023, val_loss: 0.0507, Acc:0.9459, val_acc: 0.9799
Epoch [9/100], Loss: 0.1012, val_loss: 0.0500, Acc:0.9457, val_acc: 0.9788
Epoch [10/100], Loss: 0.0998, val_loss: 0.0486, Acc:0.9469, val_acc: 0.9799
                ～～　省略　～～
Epoch [95/100], Loss: 0.0669, val_loss: 0.0420, Acc:0.9688, val_acc: 0.9888
Epoch [96/100], Loss: 0.0665, val_loss: 0.0419, Acc:0.9692, val_acc: 0.9888
Epoch [97/100], Loss: 0.0662, val_loss: 0.0419, Acc:0.9698, val_acc: 0.9888
Epoch [98/100], Loss: 0.0659, val_loss: 0.0419, Acc:0.9702, val_acc: 0.9888
Epoch [99/100], Loss: 0.0656, val_loss: 0.0419, Acc:0.9704, val_acc: 0.9888
Epoch [100/100], Loss: 0.0652, val_loss: 0.0417, Acc:0.9708, val_acc: 0.9888
'''

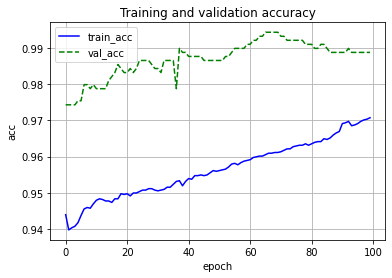
きちんと学習できているか可視化してみます。

import matplotlib.pyplot as plt
%matplotlib inline

plt.figure()
plt.plot(range(num_epochs), train_loss_list, color='blue', linestyle='-', label='train_loss')
plt.plot(range(num_epochs), val_loss_list, color='green', linestyle='--', label='val_loss')
plt.legend()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('Training and validation loss')
plt.grid()

plt.figure()
plt.plot(range(num_epochs), train_acc_list, color='blue', linestyle='-', label='train_acc')
plt.plot(range(num_epochs), val_acc_list, color='green', linestyle='--', label='val_acc')
plt.legend()
plt.xlabel('epoch')
plt.ylabel('acc')
plt.title('Training and validation accuracy')
plt.grid()

推論

訓練と評価に使用していないデータを使用して、予測をしてみようと思います。

model.eval()
with torch.no_grad():
    total = 0
    test_acc = 0
    
    n_batch = len(x_test)//batch_size
    for i_batch in range(n_batch):
        seq = cat_Tensor(x_test, i_batch, batch_size)
        labels = cat_Tensor(y_test, i_batch, batch_size)
        labels = torch.squeeze(labels, 1)
        
        seq = seq.to(device)
        labels = labels.to(device)

        outputs = model(seq)
        test_acc += (outputs.max(1)[1] == labels).sum().item()
        total += labels.size(0)
    print('精度: {} %'.format(100 * test_acc / total)) 

''' 出力
精度: 97.421875 %
'''

精度は97.42%となり、高精度での予測ができました。
ただ、高すぎる気がするので、後に検証したいと思います。