特に明記無い限り、本記事は2023年AtCoder言語アップデートの前の情報です
応用編では、典型アルゴリズム別に、最新の「AtCoder 競プロ典型90問」を30問も解説するなど、実際の問題を積極的に取り上げていきます。また、本記事のコンセプトに沿って、パラメータを変えて速度測定を行います。
2022/10/13 記事が概ね完成しましたので、「更新型記事」という表示を削除しました
記事全体の説明は基本編を参照ください。
- (1) 基本編
- (2) 応用編（本稿）
- 参考: 【競プロ】PyPy3で使える！Numpy代用ライブラリ
- 参考: 【競プロ専用】PythonでMultiSetを今度こそ
基本編では、競プロ用の入出力系スニペット、素数や組合せ等の数学関数などをとりあげています。
1. 区間演算
1.1. 累積和（基本）
区間和を何度も求める際は、予め累積和を求めてから、その差分を求めます。
問題: 競プロ典型90問_010: Score Sum Queries（★2）
累積和は愚直にも計算できるほか、itertools.accumulateを利用することでも簡単に求めることが可能です。
N = int(input())
CP = [list(map(int, input().split())) for _ in range(N)]
Q = int(input())
LR = [list(map(int, input().split())) for _ in range(Q)]
# クラス1、2をP1、P2とする -> O(N)
# この後で累積和をとるために、先頭に0を加えておく
np_T = lambda x: [list(x) for x in zip(*x)] # 転置
C, P = np_T(CP)
P1 = [0] + [p if c == 1 else 0 for p, c in zip(P, C)]
P2 = [0] + [p if c == 2 else 0 for p, c in zip(P, C)]
# P1、P2について累積和を求める -> O(N)
# 求め方その1
for n in range(1, N + 1): # P1の長さがN+1であることに注意
P1[n] += P1[n - 1]
# 求め方その2
from itertools import accumulate
P2 = list(accumulate(P2))
# 累積和の差分として、解答を出力する -> 1回ごとO(1) × Q
for l, r in LR:
print(P1[r] - P1[l-1], P2[r] - P2[l-1])
ナイーブな解法では計算量は$O(NQ)$になりますが、累積和を使うことで$O(N+Q)$になります。
速度再測定予定
| N=Q= | 10**4 | 10**5 | 10**6 |
|---|---|---|---|
| Python3.8 | 78ms | 544ms | 6317ms |
| PyPy3 | 214ms | 300ms | 1960ms |
累積和は、長い文字列の部分文字列における特定文字の数を求める、などにも応用可能です。
1.2. 累積和（いもす法）
累積和のアルゴリズムを多次元・他次数に拡張したものを、いもす法と呼びます。2次元・1次数版が頻出です。
問題: 競プロ典型90問_028: Cluttered Paper（★4）
この問題の場合、重った紙の枚数が、紙の開始点での+1と終了点での-1の累積和で求められることに気づけば、累積和を2次元に応用することで、解くことができます。
多次元の累積和は、次元ごとに逐次に累積和をとって求めるのが簡便です。
N = int(input())
S = [list(map(int, input().split())) for _ in range(N)]
H = W = 1000
# 四隅に差分をセット（2次元が重なった差分は+1とする） -> O(N)
dat = [[0] * (W + 1) for _ in range(H + 1)]
for lx, ly, rx, ry in S:
dat[ly][lx] += 1
dat[ry][lx] -= 1
dat[ly][rx] -= 1
dat[ry][rx] += 1
# 二次元累積和をとることで、datは各座標の紙の枚数になる -> O(HW)
# （各次元ごとに累積和をとる）
for y in range(H + 1):
for x in range(1, W + 1):
dat[y][x] += dat[y][x - 1]
for x in range(W + 1):
for y in range(1, H + 1):
dat[y][x] += dat[y - 1][x]
# 紙の枚数ごとに集計することで、解答を得る -> O(HW)
ans = [0] * (N + 1)
for x in range(W + 1):
for y in range(H + 1):
ans[dat[y][x]] += 1
for n in range(1, N + 1):
print(ans[n])
ナイーブな解法では計算量は$O(NHW)$になりますが、いもす法を使うことで$O(N+HW)$になります。
速度再測定予定
| N | 10**5 | 10**6 | 10**7 |
|---|---|---|---|
| Python3.8 | 584ms | 1799ms | code9 |
| PyPy3 | 258ms | 560ms | 5432ms |
1.3. BIT
問題: 競プロ典型90問_017: Crossing Segments（★7）
1点加算と閉区間[1, i]の和の取得を高速軽量に実行できるのがBIT(Binary Indexed Tree)です。とても美しいアルゴリズムとデータ構造になっています。
BITのことを、フェニック木（Fenwick tree）とも呼びます。
実装は、クラス貼り付けに便利なように、クラス部と解答部を分離しています。
class BIT:
def __init__(self, n):
self.n = len(n) if isinstance(n, list) else n
self.size = 1 << (self.n - 1).bit_length()
if isinstance(n, list): # nは1-indexedなリスト
a = [0]
for p in n: a.append(p + a[-1])
a += [a[-1]] * (self.size - self.n)
self.d = [a[p] - a[p - (p & -p)] for p in range(self.size + 1)]
else: # nは大きさ
self.d = [0] * (self.size + 1)
def __repr__(self):
p = self.size
res = []
while p > 0:
res2 = []
for r in range(p, self.size + 1, p * 2):
l = r - (r & -r) + 1
res2.append(f'[{l}, {r}]:{self.d[r]}')
res.append(' '.join(res2))
p >>= 1
res.append(f'{[self.sum(p + 1) - self.sum(p) for p in range(self.size)]}')
return '\n'.join(res)
def add(self, p, x): # O(log(n)), 点pにxを加算
assert p > 0
while p <= self.size:
self.d[p] += x
p += p & -p
def get(self, p, default=None): # O(log(n))
assert p > 0
return self.sum(p) - self.sum(p - 1) if 1 <= p <= self.n or default is None else default
def sum(self, p): # O(log(n)), 閉区間[1, p]の累積和
assert p >= 0
res = 0
while p > 0:
res += self.d[p]
p -= p & -p
return res
def lower_bound(self, x): # O(log(n)), x <= 閉区間[1, p]の累積和 となる最小のp
if x <= 0: return 0
p, r = 0, self.size
while r > 0:
if p + r <= self.n and self.d[p + r] < x:
x -= self.d[p + r]
p += r
r >>= 1
return p + 1
# Rの小さい順に並べる
# 各線分を(Li, Ri)として、新たな荷(Lk, Rk)に関して、
# Rkが前と同じでなく、Lkがそれまでの線分を通った数(*)
# の累積が求める数
# (*)は、各線分のLi+1を+1、Riを-1とした時の、点Lkまでの累積和
# ただし、L, R が1-indexedになっていることに注意
N, M = map(int, input().split())
S = [list(map(int, input().split())) for _ in range(M)]
from collections import defaultdict
T = defaultdict(list)
for L, R in S:
T[R].append(L)
bit = BIT(N)
ans = 0
for R in sorted(T.keys()):
for L in T[R]:
ans += bit.sum(L)
for L in T[R]:
bit.add(L + 1, 1)
bit.add(R, -1)
print(ans)
BITでは、1点加算、区間和取得をそれぞれ$O(\log N)$で行うことが可能です。また、同様なことはセグメント木でも可能ですが、セグメント木よりも定数倍が軽量化されています。
結果として、本問題の計算量は$O(N + M \log N)$になります。ベンチマークは、N = Mとして、円周上の全ての点について隣の隣を結んだ場合で行いました。
| N=M= | 10**4 | 10**5 | 10**6 |
|---|---|---|---|
| Python3.8 | 87ms | 708ms | 8532ms |
| PyPy3 | 100ms | 226ms | 925ms |
1.4. 転倒数
BITを使うと、バブルソートにおける置換の最小回数である「転倒数」が、簡単に求められます。
# 転倒数を求める（必要ならXは座圧しておく）
def num_inversion(X):
MAX = max(X)
bit = BIT(MAX)
res = 0
for x in X:
# 「xより左にあるxより大きい数」の個数を足す
res += bit.sum(MAX) - bit.sum(x)
bit.add(x, 1)
return res
座圧、転倒数を応用した問題がこちらです。後述する尺取法を使って、転倒数を連続的に求めています。
問題: 競プロ典型90問_089: Partitions and Inversions（★7）
# BITのclass定義を貼り付ける
# 【競プロ】PyPy3で使える！Numpy代用ライブラリ より np_x_compress を貼り付ける
N, K = map(int, input().split())
A = np_x_compress(list(map(int, input().split())), offset=1)[0]
MOD = 10 ** 9 + 7
# リストAの位置rに対して、区間[l, r]の転倒数 <= K となる最小のlを、尺取法で求める
X = []
MAX = max(A)
bit = BIT(MAX)
num_inversion = 0
bit.add(A[0], 1)
l = r = 0
while True:
# 得られた値をリストXに入れ、尺取位置を更新
if num_inversion <= K: # 転倒数がK以下ならば
X.append(l) # リストを更新
r += 1 # 区間を伸ばす
if r == N:
break
# A[r]より大きい数値が区間にいくつあるか をこれまでの転倒数に足す
num_inversion += bit.sum(MAX) - bit.sum(A[r])
bit.add(A[r], 1)
else: # 転倒数がKを超えていれば
# A[l]より小さい数値が区間にいくつあるか をこれまでの転倒数から引く
num_inversion -= bit.sum(A[l] - 1)
bit.add(A[l], -1)
l += 1 # 区間を縮める
dp = [1] # 1-indexedでのnまでの答え
dp2 = [1] # 答えの累積和
for r in range(1, N + 1):
# dp[r] = dp[l - 1] + ... + dp[r - 1]
# ただし l - 1 = X[r - 1] * 1-indexedに合わせるため
if X[r - 1] - 1 >= 0:
dp.append((dp2[r - 1] - dp2[X[r - 1] - 1]) % MOD)
else:
dp.append(dp2[r - 1] % MOD)
dp2.append((dp[-1] + dp2[-1]) % MOD)
print(dp[-1])
計算量は$O(N \log N)$です。
ベンチマークは、K=N/2として、Aは1から順に1ずつ増えていくリストにして、行いました。
| N=M= | 10**4 | 10**5 | 10**6 |
|---|---|---|---|
| Python3.8 | 77ms | 592ms | 6410ms |
| PyPy3 | 101ms | 159ms | 771ms |
1.5. セグメント木
区間の最大値や最小値を大量に求める場合は、セグメント木を使います。セグメント木の概念は複雑なので、いろいろググって参照ください。おおまかには、二分探索構造に状態を保持することで、長い区間での最大値や最小値を$O(log(区間長))$で求めるものです。
参考: AtCoder LibraryのLazy Segtreeの使い方
参考: セグメント木を徹底解説！0から遅延評価やモノイドまで
参考: セグメント木がモノイドを必要とする理由
この実装では、高速化のために再帰を使わないようにしてみました。AtCoder Libraryの実装をそのままPython化して、__repr__でprint用のコードを追加しました。
1.5.1. 通常のセグメント木
問題: 競プロ典型90問_037: Don't Leave the Spice（★5）
実装は、クラス貼り付けに便利なように、クラス部と解答部を分離しています。
class SegmentTree:
# https://qiita.com/R_olldIce/items/32cbf5bc3ffb2f84a898
def __init__(self, op, e, n):
self.n = len(n) if isinstance(n, list) else n
self.op = op
self.e = e
self.log = (self.n - 1).bit_length()
self.size = 1 << self.log
self.d = [e for _ in range(2 * self.size)]
if isinstance(n, list): self.d[self.size: self.size + self.n] = n
[self._update(i) for i in reversed(range(1, self.size))]
def __repr__(self):
l, r = 1, 2
res = []
while r <= 2 * self.size:
res.append(f'{self.d[l: r]}')
l, r = r, r << 1
return '\n'.join(res)
def set(self, p, x): # O(log n)
p += self.size
self.d[p] = x
[self._update(p >> i) for i in range(1, self.log + 1)]
def get(self, p): # O(1)
return self.d[p + self.size]
def prod(self, l, r): # [l, r) O(log n)
sml, smr = self.e, self.e
l = max(l, 0) + self.size;
r = min(r, self.n) + self.size;
while l < r:
if l & 1:
sml = self.op(sml, self.d[l])
l += 1
if r & 1:
r -= 1
smr = self.op(self.d[r], smr)
l >>= 1
r >>= 1
return self.op(sml, smr)
def all_prod(self): # O(1)
return self.d[1]
def _update(self, k):
self.d[k] = self.op(self.d[2 * k], self.d[2 * k + 1])
def max_right(self, l, f): # f(prod(l,r)) == Trueとなる最大のr, O(log n)
if l >= self.n: return self.n
l = max(l, 0) + self.size
sm = self.e
while True:
while l % 2 == 0: l >>= 1
if not f(self.op(sm, self.d[l])):
while l < self.size:
l <<= 1
if f(self.op(sm, self.d[l])):
sm = self.op(sm, self.d[l])
l += 1
return l - self.size
sm = self.op(sm, self.d[l])
l += 1
if l & -l == l: break
return self.n
def min_left(self, r, f): # f(prod(l,r)) == Trueとなる最小のl, O(log n)
if r <= 0: return 0
r = min(r, self.n) + self.size
sm = self.e
while True:
r -= 1
while r > 1 and r % 2: r >>= 1
if not f(self.op(self.d[r], sm)):
while r < self.size:
r = 2 * r + 1
if f(self.op(self.d[r], sm)):
sm = self.op(self.d[r], sm)
r -= 1
return r + 1 - self.size
sm = self.op(self.d[r], sm)
if r & -r == r: break
return 0
W, N = map(int, input().split())
S = [map(int, input().split()) for _ in range(N)]
INF = 10 ** 16
from operator import add
seg = SegmentTree(max, -INF, W) # 1点更新区間最大値取得
#seg = SegmentTree(min, INF, W) # 1点更新区間最小値取得
#seg = SegmentTree(add, 0, W) # 1点更新区間和取得
#seg = SegmentTree(二項演算子, 単位元, リスト) # (リスト, 二項演算子, 単位元)はモノイド
dp = [-INF] * (W + 1)
dp[0] = 0
seg.set(0, 0)
for L, R, V in S:
for w in range(L, R):
dp[w] = max(dp[w], seg.prod(0, w - L + 1) + V)
for w in range(R, W + 1):
dp[w] = max(dp[w], seg.prod(w - R, w - L + 1) + V)
seg = SegmentTree(max, -INF, dp)
print(dp[W] if dp[W] > 0 else -1)
計算量は、セグメント木の区間クエリーや1点更新については二分探索と同様に$O(\log W)$です。なお、通常のセグメント木は区間更新は$O(W \log W)$となりますが、若干の最適化がされており初期構築のみ$O(W)$に改善しています。ループ回数を考慮すると、クエリー部分は$O(NW \log W)$、初期構築は$O(NW)$ですので、全体の計算量はクエリー部分が効いて$O(NW \log W)$となります。
この問題は、ループの構造上、次項の遅延評価セグメント木を利用する意義はありません。
N=500固定にして、Wを動かしてベンチマークしてみました。L=1, R=M, V=1固定です。
PyPy3の高速性がとても出ています。
| W | 10**3 | 10**4 | 10**5 |
|---|---|---|---|
| Python3.8 | 1894ms | code9 | code9 |
| PyPy3 | 184ms | 1139ms | code9 |
1.5.2. 遅延評価セグメント木
問題: 競プロ典型90問_029: Long Bricks（★5）
通常のセグメント木では、区間の更新は$O(W \log W)$かかります。区間の更新にあたって、二分木構造の最小箇所のみ更新し、結果の伝搬をクエリーの時点まで遅らせることで、$O(\log W)$でできるように改善したのが、遅延評価セグメント木です。クエリーと区間更新が同程度の頻度で必要な問題に対しては、遅延評価セグメント木が有効です。
実装は、クラス貼り付けに便利なように、クラス部と解答部を分離しています。
class LazySegmentTree:
def __init__(self, op, e, mapping, composition, id_, n):
self._n = len(n) if isinstance(n, list) else n
self.op = op
self.e = e
self.mapping = mapping
self.composition = composition
self.id = id_
self.log = (self._n - 1).bit_length()
self.size = 1 << self.log
self.d = [e for _ in range(2 * self.size)]
self.lz = [id_ for _ in range(self.size)]
if isinstance(n, list): self.d[self.size: self.size + self._n] = n
[self._update(i) for i in reversed(range(1, self.size))]
def __repr__(self):
l, r = 1, 2
res = []
np_T = lambda x: [list(x) for x in zip(*x)]
while r <= self.size:
res.append(f'{np_T([self.d[l: r], self.lz[l: r]])}')
l, r = r, r << 1
res.append(f'{self.d[l: r]}')
return '\n'.join(res)
def set(self, p, x): # O(log n)
p += self.size
[self._push(p >> i) for i in reversed(range(1, self.log + 1))]
self.d[p] = x
[self._update(p >> i) for i in range(1, self.log + 1)]
def get(self, p): # O(log n)
p += self.size
[self._push(p >> i) for i in reversed(range(1, self.log + 1))]
return self.d[p]
def prod(self, l, r): # [l, r) O(log n)
if l == r: return self.e
l += self.size
r += self.size
for i in reversed(range(1, self.log + 1)):
if ((l >> i) << i) != l: self._push(l >> i)
if ((r >> i) << i) != r: self._push((r - 1) >> i)
sml, smr = self.e, self.e
while (l < r):
if l & 1:
sml = self.op(sml, self.d[l])
l += 1
if r & 1:
r -= 1
smr = self.op(self.d[r], smr)
l >>= 1;
r >>= 1;
return self.op(sml, smr)
def all_prod(self): # O(1)
return self.d[1]
def apply(self, p, f): # O(log n)
p += self.size;
[self._push(p >> i) for i in reversed(range(1, self.log + 1))]
self.d[p] = self.mapping(f, self.d[p]);
[self._update(p >> i) for i in range(1, self.log + 1)]
def apply_seg(self, l, r, f): # O(log n)
if l == r: return
l += self.size;
r += self.size;
for i in reversed(range(1, self.log + 1)):
if ((l >> i) << i) != l: self._push(l >> i)
if ((r >> i) << i) != r: self._push((r - 1) >> i)
l2, r2 = l, r
while l < r:
if l & 1:
self._all_apply(l, f);
l += 1
if r & 1:
r -= 1
self._all_apply(r, f);
l >>= 1;
r >>= 1;
l, r = l2, r2
for i in range(1, self.log + 1):
if ((l >> i) << i) != l: self._update(l >> i)
if ((r >> i) << i) != r: self._update((r - 1) >> i)
def max_right(self, l, f): # f(prod(l,r)) == Trueとなる最大のr, O(log n)
if l >= self._n: return self._n
l = max(l, 0) + self.size
for i in reversed(range(1, self.log + 1)):
self._push(l >> i)
sm = self.e
while True:
while l % 2 == 0: l >>= 1
if not f(self.op(sm, self.d[l])):
while l < self.size:
self._push(l)
l <<= 1
if f(self.op(sm, self.d[l])):
sm = self.op(sm, self.d[l])
l += 1
return l - self.size
sm = self.op(sm, self.d[l])
l += 1
if l & -l == l: break
return self._n
def min_left(self, r, f): # f(prod(l,r)) == Trueとなる最小のl, O(log n)
if r <= 0: return 0
r = min(r, self._n) + self.size
for i in reversed(range(1, self.log + 1)):
self._push((r - 1) >> i)
sm = self.e
while True:
r -= 1
while r > 1 and r % 2: r >>= 1
if not f(self.op(self.d[r], sm)):
while r < self.size:
self._push(r)
r = 2 * r + 1
if f(self.op(self.d[r], sm)):
sm = self.op(self.d[r], sm)
r -= 1
return r + 1 - self.size
sm = self.op(self.d[r], sm)
if r & -r == r: break
return 0
def _update(self, k):
self.d[k] = self.op(self.d[2 * k], self.d[2 * k + 1])
def _all_apply(self, k, f):
self.d[k] = self.mapping(f, self.d[k])
if k < self.size: self.lz[k] = self.composition(f, self.lz[k])
def _push(self, k):
self._all_apply(2 * k, self.lz[k])
self._all_apply(2 * k + 1, self.lz[k])
self.lz[k] = self.id
W, N = map(int, input().split())
S = [list(map(int, input().split())) for _ in range(N)]
# モノイドdata=(X, op, e)、作用素モノイドlazy=(M, f: X×M → X, id_)
# seg = LazySegmentTree(op, e, f, f○g, id_, X)
# opが区間値取得演算、fが更新や加算などの区間変更演算に対応する
# fは区間計算できる必要がある。よってop=区間和の場合X=[(区間和, 区間長)]とする
INF = 10 ** 16
sum2 = lambda x, y: (x[0] + y[0], x[1] + y[1]) # (区間和, 区間長)同士を統合
# 区間加算演算
add = lambda f, x: f + x
add2 = lambda f, x: (x[0] + f * x[1], x[1]) # (区間和, 区間長)にfを加算
add_comp = lambda f, g: f + g
# 区間更新演算
update = lambda f, x: f if f < INF else x
update2 = lambda f, x: (f * x[1], x[1]) if f < INF else x # 区間和計算して(値, 区間長)を更新
update_comp = lambda f, g: f if f < INF else g
# seg = LazySegmentTree(min, INF, update, update_comp, INF, W) # 区間更新・区間最小値取得
seg = LazySegmentTree(max, -INF, update, update_comp, INF, W) # 区間更新・区間最大値取得
# seg = LazySegmentTree(sum2, (0, 0), update2, update_comp, INF, [(0, 1)] * W) # 区間更新・区間和取得
# seg = LazySegmentTree(min, INF, add, add_comp, 0, W) # 区間加算・区間最小値取得
# seg = LazySegmentTree(max, -INF, add, add_comp, 0, W) # 区間加算・区間最大値取得
# seg = LazySegmentTree(sum2, (0, 0), add2, add_comp, 0, [(0, 1)] * W) # 区間加算・区間和取得
seg.apply_seg(0, W, 0)
for s in S:
L, R = s
height = seg.prod(L - 1, R) + 1
seg.apply_seg(L - 1, R, height)
print(height)
セグメント木の初期化か$O(W)$で、1回のクエリーと区間更新が$O(\log W)$となるため、ループを考慮すると計算量は$O(W + N \log W)$となります。通常のセグメント木だと区間更新が最適化版でも$O(W)$であるため、ループを考慮すると計算量が$O(NW)$となってしまい、TLEになります。遅延評価が有効な例になっています。
N=500、L=1、R=W固定にして、Wを動かしてベンチマークしてみました。
| W | 10**5 | 10**6 | 10**7 |
|---|---|---|---|
| Python3.8 | 118ms | 567ms | 8143ms |
| PyPy3 | 139ms | 293ms | 4093ms |
理論値と異なる傾向になっているようです。
セグ木は条件を満たすモノイドであればいろいろ入れることができます。AtCoder Library Practice Contestの K: Range Affine Range Sumでは、opをmod付き区間和、fをアフィン変換とすることで、遅延セグ木で解くことが可能です。なお、これまでの例のようにタプルを使うとTLEしますので、32bitの2つのパラメータをタプルではなく1つの整数に埋め込むことで、高速化を図っています。
MOD = 998244353
def modsum2(x, y):
x0, x1 = x >> 32, x % (1 << 32)
y0, y1 = y >> 32, y % (1 << 32)
return (((x0 + y0) % MOD) << 32) + x1 + y1
def affine2(f, x):
f0, f1 = f >> 32, f % (1 << 32)
x0, x1 = x >> 32, x % (1 << 32)
return (((f0 * x0 + f1 * x1) % MOD) << 32) + x1
def affine_comp(f, g):
f0, f1 = f >> 32, f % (1 << 32)
g0, g1 = g >> 32, g % (1 << 32)
return (((f0 * g0) % MOD) << 32) + (f0 * g1 + f1) % MOD
import sys
def input(): return sys.stdin.readline()[:-1]
N, Q = map(int, input().split())
a = list(map(int, input().split()))
S = [list(map(int, input().split())) for _ in range(Q)]
seg = LazySegmentTree(modsum2, 0, affine2, affine_comp, 1 << 32, [(a << 32) + 1 for a in a])
for t, l, r, *bc in S:
if t == 0:
b, c = bc
seg.apply_seg(l, r, (b << 32) + c)
else:
print(seg.prod(l, r) >> 32)
速度測定は省略します。
AtCoder Library Practice Contestの L: Lazy Segment Treeでは、opを転倒数演算、fをbit反転とすることで、遅延セグ木で解くことが可能です。
# M = [(転倒数, 0の数, 1の数)] とする
inversion = lambda x, y: (x[0] + y[0] + x[2] * y[1], x[1] + y[1], x[2] + y[2])
not_ = lambda f, x: (x[1] * x[2] - x[0], x[2], x[1]) if f else x
not_comp = lambda f, g: f ^ g
import sys
def input(): return sys.stdin.readline()[:-1]
N, Q = map(int, input().split())
A = list(map(int, input().split()))
S = [list(map(int, input().split())) for _ in range(Q)]
seg = LazySegmentTree(inversion, (0, 0, 0), not_, not_comp, False, [(0, 1 - a, a) for a in A])
for t, l, r in S:
if t == 1:
seg.apply_seg(l - 1, r, True)
else:
print(seg.prod(l - 1, r)[0])
速度測定は省略します。
2. 探索
2.1. bit全探索
2.1.1. 普通のbit全探索
なんからのon/offの選択肢を組み合わせて全探索する時に、bit全探索が活躍します。
問題: 競プロ典型90問_002: Encyclopedia of Parentheses（★3）
bitシフトと&を組み合わせてbitテストするのが、典型的な書き方です。
N = int(input())
def parentheses_repr(bit): # bitを括弧表現に変換
res = []
for n in range(N):
if (bit >> n) & 1: # bitテスト
res.append(')')
else:
res.append('(')
return ''.join(reversed(res)) # 逆順を元に戻す
for bit in range(2 ** N):
nest = 0 # 括弧の深さ
for n in range(N): # 低位ビットを括弧列の右側（逆順）とする
if (bit >> n) & 1: # bitテスト
nest += 1 # bit==1を')'として、深さを増やす
else:
nest -= 1 # bit==0を'('として、深さを減らす
if nest < 0: # 深さがマイナスになっらた条件不一致
break
if nest == 0: # 最後に深さが0なら条件一致
print(parentheses_repr(bit))
計算量は$O(2^N)$であり、Nが大きくなると急速に計算時間が増えます。N=20が出題されますので、PyPy3を使いましょう。なお、この問題に限り、固定となる両端を除いて処理をすることで、Nを2つ減らすことができます。
| N | 10 | 15 | 20 |
|---|---|---|---|
| Python3.8 | 29ms | 69ms | 1413ms |
| PyPy3 | 75ms | 87ms | 280ms |
2.1.2. 半分全列挙
前半と後半に分けて全探索をして、それらを組合せて解くことで、高速化できる場合があります。N = 40で全探索をしたくなる場面で、半分全列挙が使えるかもしれません。
問題: 競プロ典型90問_051: Typical Shop（★5）
N, K, P = map(int, input().split())
A = list(map(int, input().split()))
N0 = N // 2
# 半分に分けられない場合を先に処理しておく
if N == 1:
print(1 if A[0] <= P else 0)
exit()
def bit_search(A):
N = len(A)
res = [[] for _ in range(N + 1)]
for bit in range(2 ** N):
p = 0
k = 0
for n in range(N):
if (bit >> n) & 1: # bitテスト
p += A[n]
k += 1
if p <= P and k <= K:
res[k].append(p)
return res
# 半分全列挙
A0 = bit_search(A[:N0])
A1 = bit_search(A[N0:])
# 後半をソート
for a in A1:
a.sort()
import bisect
ans = 0
# 前半から1つずつ結果を取り、個数合計がK・数値合計がP以下の後半部を二分探索
for k0, a0 in enumerate(A0):
if K - k0 < len(A1):
for p0 in a0:
ans += bisect.bisect_right(A1[K - k0], P - p0)
print(ans)
計算量は、$O(2^{N/2}N)$になります。
| N | 35 | 40 | 45 |
|---|---|---|---|
| Python3.8 | 953ms | 5630ms | code9 |
| PyPy3 | 177ms | 753ms | 3288ms |
2.2. 二分探索
ソートされたリストから特定の値を効率良く探索するのに、二分探索が利用できます。
2.2.1. bisectの利用
探索すべきリストが予め与えられている場合は、bisectを使います。
問題: 競プロ典型90問_007: CP Classes（★3）
N = int(input())
A = sorted(list(map(int, input().split()))) # ソート O(N logN)
Q = int(input())
B = [int(input()) for _ in range(Q)]
import bisect
for b in B:
left = min(N - 1, bisect.bisect_left(A, b)) # 二分探索 O(logN)
right = max(0, bisect.bisect_right(A, b) - 1) # 二分探索 O(logN)
cp = min(abs(b - A[left]), abs(b - A[right]))
print(cp)
計算量は、ソートで$O(N \log N)$、二分探索1回あたり$O(\log N)$であるため二分探索の部分の小計は$O(Q \log N)$です。よって、全体として$O((N+Q) \log N)$になります。
ベンチマークは、AおよびBを簡単な計算により数列として生成して測定しました。
| N=Q= | 10**4 | 10**5 | 10**6 |
|---|---|---|---|
| Python3.8 | 52ms | 242ms | 2197ms |
| PyPy3 | 163ms | 259ms | 829ms |
2.2.2. 二分探索のスクラッチ実装
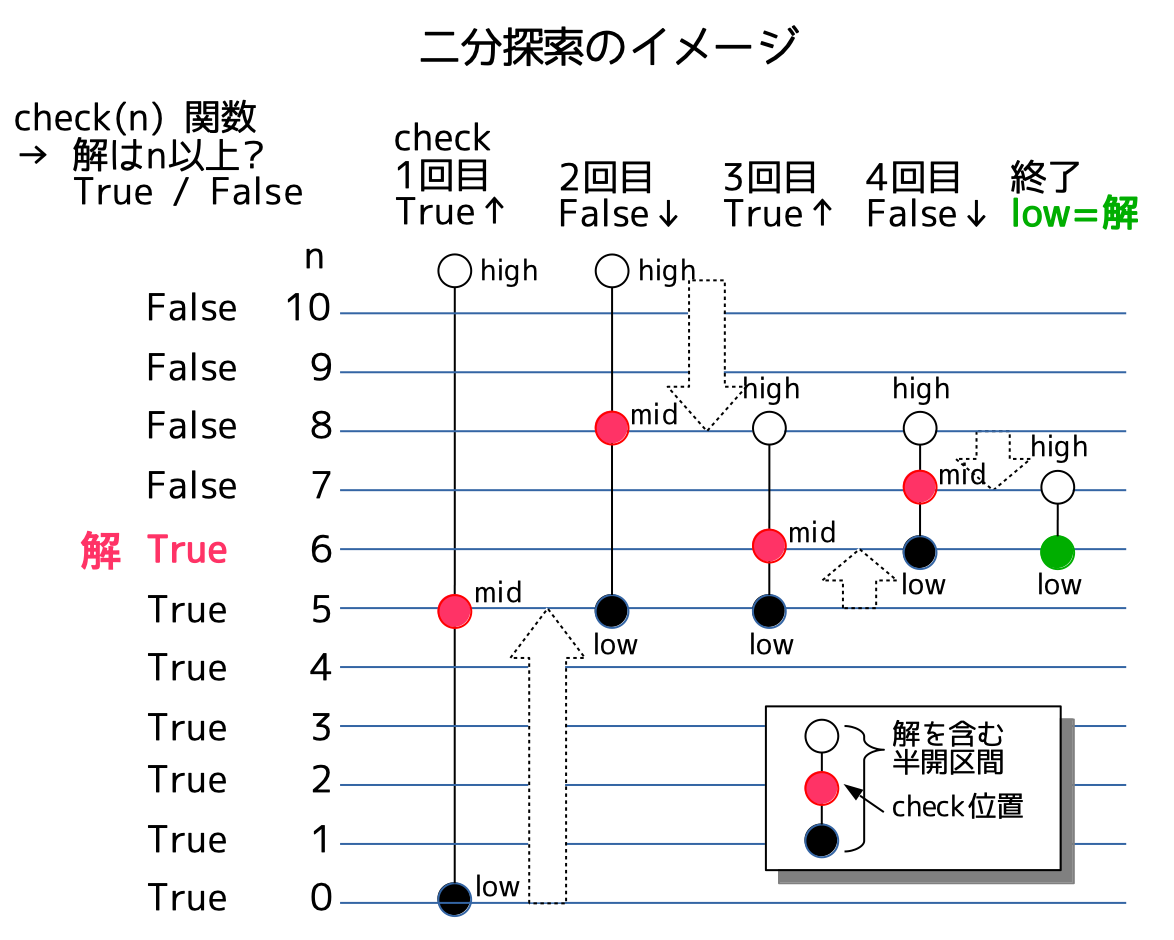
探索すべきリストが予め与えられていない場合は、二分探索をスクラッチで実装します。探索区間を順次半分に縮小していくことで、高速な探索が可能です。
問題: 競プロ典型90問_001: Yokan Party（★4）
N, L = map(int, input().split())
K = int(input())
A = list(map(int, input().split())) + [L]
# チェック関数 O(N)
def check(n): # スコアはn以上？をチェック
k = 0 # kは、ようかんの固まりの数
start = 0 # startは、現在のようかんの固まりの開始点
for a in A: # 貪欲法で固まりを切り出していく
if a - start >= n:
k += 1
start = a
return k > K # K + 1以上の固まりが得られたかどうか
# 二分探索 O(log L) × チェック関数
low, high = 0, L + 1 # 半開区間 [low, high) をめいっぱい広くとる
while low + 1 < high: # low < mid < high とする
mid = (low + high) // 2
if check(mid):
low = mid # スコアはmid以上である -> 区間の下側を短縮
else:
high = mid # スコアはmid未満である -> 区間の上側を短縮
print(low)
計算量は、二分探索について$O(\log L)$です。この例では、チェック関数が$O(N)$ですので、全体の計算量は$O(N \log L)$となります。
ベンチマークでは、N=10**5固定としてLを動かしてみました。計算量がLに関して$O(\log L)$であることがわかる結果になっています。
| L | 10**(10**1) | 10**(10**2) | 10**(10**3) |
|---|---|---|---|
| Python3.8 | 173ms | 1373ms | code9 |
| PyPy3 | 78ms | 346ms | 2657ms |
実は、check関数のFalseを1、Trueを0と置くと、check関数の出力がソート済リストとみなせるため、bisectを利用可能です。この事実をうまく使ったクラスをつくることで、二分探索のスクラッチ実装をエレガントに実現することが可能です。
# 二分探索クラス（bisect利用、けむにくメソッド）
import bisect
class BinarySearch:
# 半開区間[L, R)の広義単調増加check関数を、別に定義
# solveは、check(x)==True を満たすxのもっとも右端を求める
def __init__(self, L, R, check):
self.L, self.R = L, R
self.check = check
def __len__(self):
return self.R - self.L # 区間長
def __getitem__(self, i):
return not self.check(self.L + i) # True -> 0, False -> 1
def solve(self):
return bisect.bisect_right(self, 0) + self.L - 1
# check関数は同一
def check(x):
k = 0
start = 0
for a in A:
if a - start >= x:
k += 1
start = a
return k > K
N, L = map(int, input().split())
K = int(input())
A = list(map(int, input().split())) + [L]
bs = BinarySearch(0, L + 1, check)
print(bs.solve())
計算量、実行時間は、スクラッチ実装と同様なので、省略します。
2.2.3. MEXとGrundy数
MEXは、minimum excludedの略で、与えられた非負数値の集合に対して、その集合に含まれない最小値を求める関数です。競プロで時々登場します。様々なアルゴリズムがあるようですが、2分探索を使うことで、MEXを$O(\log \verb!ユニークなソート済みリストサイズ!)$で求めることがてきます。
Pythonには無いMultisetを使うことで、事前ソート不要でMEXを計算できるため、問題によっては計算量の削減が可能です。PythonでMultisetの実装として、こちらを使うことで、後述の実装例にそのまま適用可能です。ただし定数倍が重たいので、TLEしてしまいます。
さらにMEXの応用としてGrundy数があります。ゲームの状態が閉域を含まないグラフ(DAG)で表される時、ある状態のGrundy数は、そこからの状態遷移先のGrundy数のMEXとして、再帰的に定義されます（状態遷移ができない場合は0）。興味深いことに、Grundy数が0のゲームは後手必勝、1以上の場合は先手必勝になります。さらに、複数の独立したゲームの手番を任意に選択できる複合ゲームにおいて、各ゲームのGrundy数のXORが、複合ゲームのGrundy数になります。
問題: 競プロ典型90問_031: VS AtCoder（★6）
N = int(input())
W = list(map(int, input().split()))
B = list(map(int, input().split()))
W_max = 50
B_max = 50 + W_max * (W_max + 1) // 2 # 途中状態でのB最大値
def mex(s): # O(log len(s))、sはユニークなソート済みリスト
if len(s) == 0 or s[0] > 0: # 0は頻出なのでショートカット処理
return 0
def check(n):
return n - 1 == s[n - 1]
low, high = 1, len(s) + 1
while low + 1 < high:
mid = (low + high) // 2
if check(mid):
low = mid
else:
high = mid
return low
def _mex(s): # O(len(s))だが定数倍が速い、sはユニークなソート済みリスト
n = -1
for n, x in enumerate(s):
if n != x:
return n
return n + 1
grundy = [[0] * (B_max + 1) for _ in range(W_max + 1)]
for w in range(W_max + 1):
for b in range(B_max + 1):
if w == 0 and b <= 1 or b > B_max - w * (w + 1) // 2: # Bの計算不要領域
continue
s = set()
if w >= 1:
s.add(grundy[w - 1][b + w])
if b >= 2:
for k in range(1, b // 2 + 1):
s.add(grundy[w][b - k])
grundy[w][b] = mex(sorted(s))
ans = 0
for w, b in zip(W, B):
ans ^= grundy[w][b]
print('First' if ans > 0 else 'Second')
Grundy数は再帰的に求めるのですが、単純に再帰をPyPy3で実装すると遅くなるため、再帰を使わない方法で実装します。再帰に関する注意は、本記事の基本編を参照してください。
計算量は難しいですが、解説によると$O(N + max(B_i, W_i)^5)$とのことです。先に$max(B_i)$、$max(W_i)$まで事前計算しますので、$N$の定数項は小さく、$O(max(B_i, W_i)^5)$が支配的です。
ベンチマークでは、N=10**5固定として、B=Wを動かしてみます。5乗の効果で急速に値が変化することがわかります。
| B=W= | 30 | 50 | 70 |
|---|---|---|---|
| Python3.8 | 232ms | 2138ms | 10400ms |
| PyPy3 | 170ms | 883ms | 3799ms |
2次元リストの1次元化も試してみましたが、むしろ速度悪化しました。
2.3. 周期性／ダブリング
周期性を活かした探索問題は、アルゴリズムに特定の名前はついていませんが、頻出かつ実装が重いので、掲載しておきます。
答え用、状態遷移用、開始地点からの遷移idx用、ループカウンタの4つの配列を前処理することで、周期をみつけて、巨大カウンタが指し示す答えを求めます。
問題: 競プロ典型90問_058: Original Calculator（★4）
N, K = map(int, input().split())
M = 10 ** 5
# 周期内の答えを前処理で求めておく
ans = [i for i in range(M)]
# 状態遷移 idx → next_index を求める
next_ = []
for i in range(M):
x = ans[i]
y = sum(map(int, list(str(x))))
z = (x + y) % M
next_.append(z)
# 開始地点からの遷移idx、
# ループ開始カウンタ:cnt_begin_loop、
# ループ合流カウンタ:cnt_merge_loopを求める
idx = [N]
cnt = [-1] * M
cnt[N] = 0
for c in range(1, M + 1): # カウンタは1〜M
next_idx = next_[idx[-1]]
if cnt[next_idx] != -1:
cnt_begin_loop = cnt[next_idx]
cnt_merge_loop = c
break
cnt[next_idx] = c
idx.append(next_idx)
# 周期性を意識してカウンタKの剰余を取る
if K >= cnt_begin_loop:
K -= cnt_begin_loop
K %= (cnt_merge_loop - cnt_begin_loop)
K += cnt_begin_loop
# カウンタK→idx→答え
print(ans[idx[K]])
計算量は、周期をMとして、$O(M)$です。周期内は事前計算をしているとともに、Pythonのint型は強力であるため、Kがいくら大きくなっても影響ありません。ベンチマークは、初期値N=1固定とします。
| K | 10**18 | 10**10000 |
|---|---|---|
| Python3.8 | 157ms | 154ms |
| PyPy3 | 129ms | 123ms |
この問題は、2の冪乗先の遷移を前計算するダブリングという手法を使うことで、若干計算量が大きくなりますが、シンプルに解答可能です。
N, K = map(int, input().split())
M = 10 ** 5
T = K.bit_length() # 2^T > N
next_ = []
# 1つ先の状態遷移を求める
next_.append([(m + sum(map(int, list(str(m))))) % M for m in range(M)])
# 2^t(<= N)個先の状態遷移を前計算する
for t in range(1, T):
next_.append([next_[-1][next_[-1][m]] for m in range(M)])
# ダブリング
ans = N
for t in range(T):
if (K >> t) & 1:
ans = next_[t][ans]
print(ans)
計算量は、$O(M \log N)$です。
速度測定予定
3. グラフ
グラフ構造特有のアルゴリズムです。迷路などの2次元構造を探索する際も利用します。
3.1. 深さ優先探索(DFS)
グラフや迷路のゴールにたどり着けるかを調べる場合や全探索する場合に、DFSが使えます。
問題: 競プロ典型90問_003: Longest Circular Road（★4）
DFSは再帰とスタックの双方での記述が可能です。一般的にはスタックの方が高速に処理できます。一方、再帰の方は、帰りがけ処理を簡明に記述することが可能です。
3.1.1. 再帰
検知した新たな探索場所を再帰で呼び出します。また、訪問済みリストをseenで管理します。行きがけや帰りがけに、問題固有の処理を記述したり、呼び出しパラメータに問題固有のパラメータを加えたりすることで、さまざまなグラフ問題を解くことができます。
なお、再帰数の最大値を上げることを忘れないようにしましょう。
N = int(input())
S = [list(map(int, input().split())) for _ in range(N - 1)]
# 無向グラフの典型入力
from collections import defaultdict
adj = defaultdict(list)
for a, b in S:
adj[a-1].append(b-1)
adj[b-1].append(a-1)
import sys
sys.setrecursionlimit(10 ** 9)
def dfs(pos, seen, dist): # dist（ここまでの距離）は問題固有のパラメータ
seen[pos] = True
# 行きがけ順の処理（最大距離と都市を求める）
global max_dist, max_pos
if max_dist < dist:
max_dist = dist
max_pos = pos
# 次の位置を探索する
for next_ in adj[pos]:
if not seen[next_]:
dfs(next_, seen, dist + 1)
# 帰りがけ順の処理（この問題では記載なし）
max_dist = 0
max_pos = 0
dfs(0, [False] * N, 0)
dfs(max_pos, [False] * N, 0)
print(max_dist + 1)
計算量は$O(N)$です。ベンチマークはグラフの特徴が際立つ2種類を行います。
- バス型: 隣通しの都市が直結するようにグラフを構成
- ツリー型: 都市0から残り全ての都市が直結するようにグラフを構成
なお、本問題は検索処理を2周していますので、時間も倍かかっています。
| N | 10**4 | 10**5 | 10**6 | |
|---|---|---|---|---|
| バス型 | Python3.8 | 56ms | 383ms | 4289ms |
| PyPy3 | 191ms | 416ms | 4571ms | |
| ツリー型 | Python3.8 | 42ms | 184ms | 2195ms |
| PyPy3 | 99ms | 150ms | 899ms |
バス型でのPyPy3が遅いことに注目しましょう。本記事の基本編でも述べている通り、PyPy3は再帰がとても遅いです。ツリー型では再帰が深くないため影響は出ていません。
一般的に、同じ言語では再帰を使う方が遅くなるのですが、Python使いにとっては、さらに「PyPy3が封じられる」という二重苦になります。よって、なるべく、再帰を使わない記述をできるようにしましょう。
3.1.2. スタック（行きがけ処理）
検知した新たな探索場所をtodoとしてlistを使ったLIFOスタック構造にpushして、スタックが無くなるまでpopして処理をします。再帰と比較してやや複雑ですが、性能は向上します。
N = int(input())
S = [list(map(int, input().split())) for _ in range(N - 1)]
# 無向グラフの典型入力
from collections import defaultdict
adj = defaultdict(list)
for a, b in S:
adj[a-1].append(b-1)
adj[b-1].append(a-1)
def dfs(start):
todo = [(0, start)] # 初期探索場所をpush
seen = [False] * N
# 問題固有の前処理
max_dist = 0
max_pos = None
while todo:
dist, pos = todo.pop() # LIFOでpop
if seen[pos]:
continue
seen[pos] = True
# 行きがけ順の処理（最大距離と都市を求める）
if max_dist < dist:
max_dist = dist
max_pos = pos
# 次の位置を探索する
for next_ in adj[pos]:
todo.append((dist + 1, next_))
return max_dist, max_pos
_, max_pos = dfs(0)
max_dist, _ = dfs(max_pos)
print(max_dist + 1)
こちらも計算量は$O(N)$です。再帰が深いバス型では再帰よりも全般的に高速で、なおかつPyPy3の高速性も発揮されています。一方、再帰が浅いツリー型では再帰と同等か、Pythondでは若干遅くなっています。再帰の悪影響が少ない中で少しコードが複雑になったペナルティが出ているものと思います。
| N | 10**4 | 10**5 | 10**6 | |
|---|---|---|---|---|
| バス型 | Python3.8 | 47ms | 252ms | 2750ms |
| PyPy3 | 90ms | 134ms | 783ms | |
| ツリー型 | Python3.8 | 48ms | 232ms | 2667ms |
| PyPy3 | 81ms | 143ms | 930ms |
3.1.3. スタック（帰りがけ処理）
スタックの場合は、帰りがけ処理の記述が複雑になります。dfsスタック版の帰りがけ処理のコードは、いろいろググりましたが参考となるものがありませんでしたので、完全オリジナルです。
ビット反転で帰りがけ順をあらわすテクニックは、オイラーツアーの記事のいくつかで使われていました。
N = int(input())
S = [list(map(int, input().split())) for _ in range(N - 1)]
# 無向グラフの典型入力
from collections import defaultdict
adj = defaultdict(list)
for a, b in S:
adj[a-1].append(b-1)
adj[b-1].append(a-1)
def dfs(pos):
todo = [(0, ~pos), (0, pos)] # 初期探索場所をpush
seen = [False] * N
finished = [False] * N
# 問題固有の前処理
max_dist = 0
max_pos = None
while todo:
dist, pos = todo.pop() # LIFOでpop
if pos >= 0:
if finished[pos]:
continue
seen[pos] = True
# 行きがけ順の処理（最大距離と都市を求める）
if max_dist < dist:
max_dist = dist
max_pos = pos
# 次の位置を探索する
for next_ in adj[pos]:
if seen[next_]:
continue
todo.append((dist + 1, ~next_)) # 帰りがけはビット反転
todo.append((dist + 1, next_))
else:
pos = ~pos # ビット反転を戻す
if finished[pos]:
continue
finished[pos] = True
# 帰りがけ順の処理（この問題では記載なし）
return max_dist, max_pos
_, max_pos = dfs(0)
max_dist, _ = dfs(max_pos)
print(max_dist + 1)
行きがけ処理の場合と比べて、速度は犠牲になります。バス型だと再帰よりはまだ速いですが、ツリー型だと再帰よりもはっきりと遅くなります。
| N | 10**4 | 10**5 | 10**6 | |
|---|---|---|---|---|
| バス型 | Python3.8 | 54ms | 286ms | 3230ms |
| PyPy3 | 96ms | 150ms | 1020ms | |
| ツリー型 | Python3.8 | 53ms | 288ms | 3229ms |
| PyPy3 | 92ms | 168ms | 1194ms |
3.1.4. オイラーツアー
帰りがけ処理を使うと、木を根から巡回するオイラーツアーにおいて、各頂点の訪問順の最初と最後をすべて求めることができます。この結果を使うと、部分木に対するクエリーを区間クエリーに変換することができます。
問題: ABC202_E - Count Descendants
import sys
def input(): return sys.stdin.readline()[:-1]
N = int(input())
P = list(map(int, input().split()))
Q = int(input())
query = [list(map(int, input().split())) for _ in range(Q)]
# 親リストPを使った無向グラフの典型入力
from collections import defaultdict
adj = defaultdict(list)
for c, p in enumerate(P):
adj[p-1].append(c+1)
adj[c+1].append(p-1)
INF = 10 ** 18
# オイラーツアーと深さを算出
def dfs(pos):
todo = [(0, ~pos), (0, pos)]
in_ = [INF] * N
out = [INF] * N
depth = [INF] * N
count = 0
while todo:
dist, pos = todo.pop()
if pos >= 0:
if out[pos] < INF:
continue
in_[pos] = count
count += 1
depth[pos] = dist
for next_ in adj[pos]:
if in_[next_] < INF:
continue
todo.append((dist, ~next_))
todo.append((dist + 1, next_))
else:
pos = ~pos
if out[pos] < INF:
continue
out[pos] = count
count += 1
return in_, out, depth
in_, out, depth = dfs(0)
# 深さごとにin_の値を昇順に保持
depth_in = defaultdict(list)
for n in range(N):
depth_in[depth[n]].append(in_[n])
for d in depth_in.keys():
depth_in[d].sort()
# クエリーを答える
import bisect
for U, D in query:
u_in = in_[U - 1]
u_out = out[U - 1]
ans = bisect.bisect_left(depth_in[D], u_out) - bisect.bisect_left(depth_in[D], u_in)
print(ans)
速度測定は省略します。
3.2. 幅優先探索(BFS)
グラフや迷路の最短経路を調べる場合などに、BFSが使えます。全探索にも使えるため、問題はDFSと同一とします。
DFSのLIFOスタックを、dequeを使ったFIFOキューに変更するだけで、BFSが作れます。
N = int(input())
S = [list(map(int, input().split())) for _ in range(N - 1)]
# 無向グラフの典型入力
from collections import defaultdict
adj = defaultdict(list)
for a, b in S:
adj[a-1].append(b-1)
adj[b-1].append(a-1)
from collections import deque
def bfs(start):
todo = deque()
todo.append((0, start)) # 初期探索場所をpush
seen = [False] * N
# 問題固有の前処理
max_dist = 0
max_pos = None
while todo:
dist, pos = todo.popleft() # FIFOでpop
if seen[pos]:
continue
seen[pos] = True
# 行きがけ順の処理（最大距離と都市を求める）
if max_dist < dist:
max_dist = dist
max_pos = pos
# 次の位置を探索する
for next_ in adj[pos]:
todo.append((dist + 1, next_))
return max_dist, max_pos
_, max_pos = bfs(0)
max_dist, _ = bfs(max_pos)
print(max_dist + 1)
計算量は$O(N)$です。ベンチマークは、当然ながらDFS行きがけと同等の結果になります。
| N | 10**4 | 10**5 | 10**6 | |
|---|---|---|---|---|
| バス型 | Python3.8 | 49ms | 236ms | 2650ms |
| PyPy3 | 124ms | 139ms | 754ms | |
| ツリー型 | Python3.8 | 46ms | 237ms | 2563ms |
| PyPy3 | 109ms | 155ms | 995ms |
3.3. ワーシャルフロイド法
グラフの重み付き最短経路を調べる場合に、ワーシャルフロイド法が使えます。
一般的には、次項のダイクストラ法の方が高速ですが、以下のような問題特徴の場合は、ワーシャルフロイド法が使える可能性があります。
- 頂点数Nが比較的少ない（$\leqq 500$）
- 全ての頂点間の距離を求める必要がある
- 辺の数Mが稠密である($max(M) \approx N(N-1)$)
- 辺の重みに負の数が含まれる
※太字が該当しない場合は、このあとで説明するダイクストラ法を全点に適用する方が、速い場合があります。
なお、典型90でも「087 - Chokudai's Demand（★5）」がワーシャルフロイド法をテーマにしていますが、複合問題で難しいため、シンプルな以下を例題とします。
問題: ABC208_D: Shortest Path Queries 2
N, M = map(int, input().split())
S = [list(map(int, input().split())) for _ in range(M)]
INF = 10 ** 16
# ワーシャルフロイド法の初期設定としての、ノード間のコスト設定
dist = [INF] * N * N
def _(i, j): return i * N + j # 1次元化簡易記述（基本編参照）
for a, b, c in S:
dist[_(a-1, b-1)] = c # この問題は一方通行であることに注意
# dist[b-1][a-1] = c
for n in range(N):
dist[_(n, n)] = 0
ans = 0
# ワーシャルフロイド法
for k in range(N): # 中継ノード
for s in range(N):
for t in range(N):
dist[_(s, t)] = min(dist[_(s, t)], dist[_(s, k)] + dist[_(k, t)]) # 中継ノードを介したコスト改善
if dist[_(s, t)] < INF: # 全てのs,t,kでの総和
ans += dist[_(s, t)]
print(ans)
ワーシャルフロイド法の計算量は、$O(N^3)$です。ベンチマークは、全ての頂点間をコスト1の辺で結んだ状態で行いました。3乗の効果で急速に値が変化することがわかります。生Pythonだと力不足なようです。
| N | 200 | 400 | 800 |
|---|---|---|---|
| Python3.8 | 8475ms | code9 | code9 |
| PyPy3 | 130ms | 374ms | 2263ms |
3.4. ダイクストラ法
グラフの重み付き最短経路を高速に調べる場合に、ダイクストラ法が使えます。
この問題は、街1から街kまでの最短経路と、街kから街Nまでの最短経路との合計が、解答になります。
無理して再帰で書くこともできますが、再帰にしない方が自然です。
N, M = map(int, input().split())
S = [list(map(int, input().split())) for _ in range(M)]
# 距離付き無向グラフの典型入力
from collections import defaultdict
adj = defaultdict(list)
for a, b, c in S:
adj[a-1].append((b-1, c))
adj[b-1].append((a-1, c))
INF = float('inf')
import heapq
def dijkstra(start):
dist = [INF] * N
dist[start] = 0
h = []
heapq.heappush(h, (0, start))
while h:
d, pos = heapq.heappop(h) # 最短距離の頂点
if d != dist[pos]:
continue
for next_, cost in adj[pos]: # 隣接候補
next_d = d + cost
if next_d < dist[next_]:
dist[next_] = next_d # 最短距離を更新
heapq.heappush(h, (next_d, next_)) # 最短距離をヒープキューで管理
return dist
d1 = dijkstra(0) # 街1から各街への距離
d2 = dijkstra(N-1) # 街Nから各街への距離
for k in range(N):
print(d1[k] + d2[k])
ダイクストラ法の計算量は、グラフの辺が頂点と同程度の量であるような疎な状態（本問題が好例です）を前提とすると$O(N \log N)$です。ベンチマークは、M = N - 1で、辺のコストを全て1として、DFS/BFSと同様に行いました。
なお、問題の特性からダイクストラを2回実行していることに注意ください。1回だけの実行時間の目安は、ベンチマークの半分になります。
| N | 10**4 | 10**5 | 10**6 | |
|---|---|---|---|---|
| バス型 | Python3.8 | 52ms | 322ms | 3600ms |
| PyPy3 | 101ms | 276ms | 970ms | |
| ツリー型 | Python3.8 | 58ms | 380ms | 4584ms |
| PyPy3 | 170ms | 259ms | 1527ms |
3.5. 01-BFS
ダイクストラ法を使う場面で、辺の長さが0または1の場合、BFSを応用して$O(N)$で解くことができます。
問題: 競プロ典型90問_043: Maze Challenge with Lack of Sleep（★4）
H, W = map(int, input().split())
rs, cs = map(int, input().split())
rt, ct = map(int, input().split())
S = [input() for _ in range(H)]
from collections import deque
def _(x, i): return x * 4 + i # 1次元化簡易記述（基本編参照）
def _pos(r, c): return r * W + c # 1次元化簡易記述（基本編参照）
start = _pos(rs - 1, cs - 1) # 速度重視のため1次元にする
goal = _pos(rt - 1, ct - 1)
DIRS = [(-1, 0), (1, 0), (0, -1), (0, 1)]
INF = 10 ** 16
def bfs(start):
todo = deque()
costs = [INF] * (H * W * 4) # 速度重視のため1次元にする
for i, _dir in enumerate(DIRS):
todo.append((start, i)) # 問題特有のパラメータである方向全種を初期push
costs[_(start, i)] = 0
while todo:
pos, i = todo.popleft() # FIFOでpop
cost = costs[_(pos, i)]
# ゴール処理
if pos == goal:
return cost
# 次の位置を探索する（01-bfs）
h, w = pos // W, pos % W
for j, (dh, dw) in enumerate(DIRS):
hh, ww = h + dh, w + dw
next_ = _pos(hh, ww)
if i == j: # 同じ方向なら0
if (0 <= hh < H and 0 <= ww < W and
costs[_(next_, j)] > cost and S[hh][ww] == '.'):
costs[_(next_, j)] = cost
todo.appendleft((next_, j)) # 0は左にpush
else: # 方向転換するなら1
if (0 <= hh < H and 0 <= ww < W and
costs[_(next_, j)] > cost + 1 and S[hh][ww] == '.'):
costs[_(next_, j)] = cost + 1
todo.append((next_, j)) # 1は右にpush
return INF
print(bfs(start))
01-BFSで解ける問題は、ダイクストラ法ではTLEになるようにセッティングされています。そのため、遅いPython（PyPy3を含む）を使った01-BFSは、素直に実装するとTLEになる可能性が高いです。実際、上記の解答だと実測921msですが、costsを2次元にすると実測1500〜1700msになり、さらに縦横を別次元にする素直な記述だとTLEになります。リストの次元を減らすことで定数倍の高速化が可能です。
計算量は、$O(H \times W)$となります。ベンチマークは、壁の無い迷路において、左上スタート、右下ゴール、すなわち1回だけ移動方向が変わるのが解答となるパターンで行います。
| H=W= | 500 | 1000 | 2000 |
|---|---|---|---|
| Python3.8 | 914ms | 3505ms | code9 |
| PyPy3 | 172ms | 334ms | 1173ms |
3.6. Union Find／最小全域木
グループ分け問題はUnion Findで解きます。
Union Findのことを、DSU（Disjoint Set Union）とも呼びます。
問題: 競プロ典型90問_012: Red Painting（★4）
実装は、クラス貼り付けに便利なように、クラス部と解答部を分離しています。
class UnionFind:
# 参考 https://note.nkmk.me/python-union-find/
# 参考 https://ikatakos.com/pot/programming_algorithm/data_structure/union_find_tree
def __init__(self, n):
self.parents = [-1] * n # 負は親（数値は木の大きさ）、非負は子（数値は親インデックス）
def root(self, x): # 木の根 非再帰版 O(α(N))
stack = []
while self.parents[x] >= 0:
stack.append(x)
x = self.parents[x]
for y in stack:
self.parents[y] = x
return x
def union(self, x, y): # 木を結合する O(α(N))
x = self.root(x)
y = self.root(y)
if x == y:
return
if self.parents[x] > self.parents[y]:
x, y = y, x
self.parents[x] += self.parents[y]
self.parents[y] = x
def size(self, x): # 木のサイズ O(α(N))
return -self.parents[self.root(x)]
def same(self, x, y): # 同じ木に属するか O(α(N))
return self.root(x) == self.root(y)
def roots(self): # O(N)
return [i for i, x in enumerate(self.parents) if x < 0]
def group_count(self): # グループ数 O(N)
return len(self.roots())
H, W = map(int, input().split())
Q = int(input())
q = [list(map(int, input().split())) for _ in range(Q)]
S = [[False] * W for _ in range(H)]
uf = UnionFind(W * H)
for t, *params in q:
if t == 1:
r, c = map(lambda x: x - 1, params)
S[r][c] = True
for rd, cd in [(-1, 0), (0, -1), (1, 0), (0, 1)]:
rr, cc = r + rd, c + cd
if 0 <= rr < H and 0 <= cc < W and S[rr][cc]:
uf.union(r * W + c, rr * W + cc)
else:
ra, ca, rb, cb = map(lambda x: x - 1, params)
if S[ra][ca] and S[rb][cb] and uf.same(ra * W + ca, rb * W + cb):
print('Yes')
else:
print('No')
計算量は、$O(\alpha(H \times W)\times Q)$となります。ただし、$\alpha(x)$は「アッカーマンの逆関数」を表します。ベンチマークは、左上から順にマスを赤色で塗っていく、すなわち解答は1となるパターンで行います。クエリー数Q=100000は固定です。
| H=W= | 1000 | 2000 | 5000 |
|---|---|---|---|
| Python3.8 | 457ms | 562ms | 1272ms |
| PyPy3 | 157ms | 215ms | 608ms |
「アッカーマンの逆関数は、ほとんど定数」とのことですが、ベンチマーク結果にはあらわれていません。これは、ベンチマーク準備やUnionFindの初期化に、$O(H \times W \times Q)$かかっていることが、影響を与えたためと思われます。
また、UnionFindを使うと、連結グラフの全ての頂点を通る部分木で辺の重み合計が最小のものを求める、最小全域木問題にも対応できます。
問題: 競プロ典型90問_049: Flip Digits 2（★6）
UnifonFindのクラスをそのまま流用します。ベンチマークは省略します。
N, M = map(int, input().split())
Q = sorted([list(map(int, input().split())) for _ in range(M)], key=lambda x: x[0]) # 辺の重みをソート
uf = UnionFind(N + 1)
ans = 0
for C, L, R in Q: # 重みが小さい辺から確認
if uf.same(L - 1, R): # 閉路を作るなら辺を追加しない
continue
uf.union(L - 1, R) # 閉路を作らないなら辺を追加する
ans += C # 追加した辺の重みを加算
if uf.size(0) < N + 1: # 全ての頂点を通ったかの確認
ans = -1
print(ans)
3.7. その他の木アルゴリズム
木に関しては様々なアルゴリズムがあります。以下の問題には、頂点の深さ、 DFS順序、k個上の頂点、LCA（最近共通祖先）など、いくつかのアルゴリズム要素が複合されています。
問題: 競プロ典型90問_035: Preserve Connectivity（★7）
N = int(input())
S = [list(map(int, input().split())) for _ in range(N - 1)]
Q = int(input())
T = [list(map(int, input().split())) for _ in range(Q)]
# 無向グラフの典型入力
from collections import defaultdict
adj = defaultdict(list)
for a, b in S:
adj[a-1].append(b-1)
adj[b-1].append(a-1)
INF = 10 ** 16
depth = [INF] * N
dfs_seq = [INF] * N
# 0を根にして深さdepthとDFS順序dfs_seqを求める
todo = [(0, 0)]
count = 0
while todo:
d, pos = todo.pop()
if dfs_seq[pos] < INF:
continue
dfs_seq[pos] = count
count += 1
depth[pos] = d
for next_ in adj[pos]:
todo.append((d + 1, next_))
# 2 ** k 個上の頂点を前計算する（k < log2 N）
import math
K = int(math.log2(N)) + 1
up2 = [[INF] * N for _ in range(K)]
for a, b in S:
if depth[a-1] < depth[b-1]:
up2[0][b-1] = a-1
else:
up2[0][a-1] = b-1
for k in range(1, K):
for p in range(N):
if up2[k-1][p] < INF:
up2[k][p] = up2[k-1][up2[k-1][p]]
else:
up2[k][p] = INF
# k個上の頂点をダブリングで求める（k <= depth[n]）
def up(n, p):
k = 0
while n > 0:
if n % 2:
p = up2[k][p]
if p == INF:
break
n //= 2
k += 1
return p
# 最小共通祖先LCAを求める
def lca(p, q):
# 深い方のdepthを、浅い方に揃える
if depth[p] > depth[q]:
p, q = q, p
d = depth[p]
q = up(depth[q] - d, q)
# depthをそろえた頂点が同じであれば、それが答え
if p == q:
return p
# さもなければ、前計算した2**k個上の頂点を順に見比べて、答えを探索する
k = K - 1
while k >= 0:
p1, q1 = up2[k][p], up2[k][q]
if p1 != q1:
p, q = p1, q1
else:
ans = p1
k -= 1
return ans
# 2点距離を求める
def dist(p, q):
return depth[p] + depth[q] - depth[lca(p, q)] * 2
# 問題への解答
for K_V in T:
# 頂点をdfs順に並べ直す
V = [x[-1] for x in sorted([(dfs_seq[n-1], n-1) for n in K_V[1:]])]
# 2個ずつ取り出して周遊ルートを作り、距離の総合計//2が答え
ans = 0
for p, q in zip(V, V[1:] + [V[0]]):
ans += dist(p, q)
ans //= 2
print(ans)
計算量は$O((N + \sum_{i=1}^Q K_i) \log N)$です。
ベンチマークは、木をバス型とツリー型の二種、Q=N-1で各クエリーは頂点1と1を除く各頂点1つずつの2頂点（=ツリー型の場合の各辺の2頂点）のみ、というセットで行いました。
| N | 10**4 | 10**5 | 10**6 | |
|---|---|---|---|---|
| バス型 | Python3.8 | 149ms | 1445ms | code9 |
| PyPy3 | 156ms | 343ms | 2433ms | |
| ツリー型 | Python3.8 | 110ms | 909ms | 10243ms |
| PyPy3 | 137ms | 299ms | 2152ms |
ツリー型の場合は、各辺の隣接頂点がクエリーですので、LCAを求める手間が軽くなります。一方バス型は数万単位の距離の頂点間でのLCAを求めていることになります。バス型とツリー型とで、ベンチマーク結果の差はわずかですので、効率的にLCAを求めていることがわかります。
3.8. トポロジカルソート
有向グラフに対して、辺の向きを順方向に揃えるように頂点を並び替えすることを、トポロジカルソートと呼びます。典型90の問71の小課題2が、トポロジカルソート問題になっています。
問題: 競プロ典型90問_071: Fuzzy Priority（★7） 小課題2のみ
N, M, K = map(int, input().split())
S = [list(map(int, input().split())) for _ in range(M)]
# 有向グラフの典型入力
from collections import defaultdict
adj = defaultdict(list)
deg = [0] * N
for a, b in S:
adj[a-1].append(b-1)
deg[b-1] += 1 # 入ってくる辺の数をdegとする
# トポロジカルソート
from collections import deque
todo = deque()
ans = []
for n in range(N): # deg == 0 の頂点を全てキューに入れる
if deg[n] == 0:
todo.append(n)
while todo:
pos = todo.popleft()
ans.append(pos)
for next_ in adj[pos]: # 取り出した頂点の行き先のdegを-1する
deg[next_] -= 1
if deg[next_] == 0: # deg == 0 になったらキューに入れる
todo.append(next_)
# deg > 0 が残っていたらソート未完成
if any([d > 0 for d in deg]):
print(-1)
exit()
# 結果(各indexを+1する)が小課題2の答え
print(*[a + 1 for a in ans])
計算量は$O(N+M)$です。
ベンチマークは、木に限定して、バス型とツリー型について、根の方向に向けて有向グラフを作って行いました。小課題2限定ですのでK=1とします。例えばバス型については、頂点を逆向きに並べる解答になります。
| N | 10**4 | 10**5 | 10**6 | |
|---|---|---|---|---|
| バス型 | Python3.8 | 46ms | 216ms | 2406ms |
| PyPy3 | 99ms | 156ms | 804ms | |
| ツリー型 | Python3.8 | 45ms | 213ms | 2287ms |
| PyPy3 | 105ms | 156ms | 938ms |
3.9. Low Link
グラフの「橋」と「関節点」を高速で求めるのがLow Linkです。Low Linkが必要になるケースは、典型90やABCではあまり出て来ませんが、知っておくとAHCなどで便利です。
以下では、あまり見かけない、非再帰のLow Linkをコーディングしてみました。
N, M = map(int, input().split())
S = [list(map(int, input().split())) for _ in range(M)]
from collections import defaultdict
adj = defaultdict(list)
for a, b in S:
adj[a - 1].append(b - 1)
adj[b - 1].append(a - 1)
INF = 10 ** 16
class LowLink:
def __init__(self):
self.k = 0
self.ord = [None] * N # seen を兼ねる
self.low = [INF] * N
self.finished = [False] * N
self.aps = set()
self.bridges = set()
for u in range(N):
if self.ord[u] is None:
self.dfs(u)
def dfs(self, s):
todo = [(s, -1)] # 初期探索場所をpush（スタート地点の帰りがけは不要）
num_child_of_root = 0
while todo:
u, par = todo.pop() # LIFOでpop
if u >= 0:
if self.finished[u]:
continue
# 行きがけ順の処理（DFS木の訪問順にordを付与）
self.k += 1
self.ord[u] = self.k
self.low[u] = self.k
# 次の位置を探索する
for v in adj[u]:
if v == par:
continue
if self.ord[v] is not None:
# 後退辺を発見したら、lowを更新する
self.low[u] = min(self.low[u], self.low[v])
continue
todo.append((~v, u)) # 帰りがけはビット反転
todo.append((v, u))
else:
v = ~u # ビット反転を戻す
if self.finished[v]:
continue
self.finished[v] = True
# 帰りがけ順の処理（後退辺の影響を逆伝搬する）
self.low[par] = min(self.low[par], self.low[v])
# 頂点が関節点となる条件
if par == s:
num_child_of_root += 1
elif self.ord[par] <= self.low[v]:
self.aps.add(par)
# 辺が橋となる条件
if self.ord[par] < self.low[v]:
self.bridges.add((min(par, v), max(par, v)))
if num_child_of_root >= 2:
self.aps.add(s)
return
print(len(LowLink().bridges))
# LowLink().aps は関節点
計算量は$O(N + M)$です。
ベンチマークは、頂点の半分ずつで輪を作り、それらを1箇所ずつで接続したグラフで行いました。接続箇所が橋になります。
| N | 10**4 | 10**5 | 10**6 |
|---|---|---|---|
| Python3.8 | 51ms | 300ms | 3389ms |
| PyPy3 | 94ms | 141ms | ８８２ms |
3.10. 強連結成分分解（SCC）
有向グラフをループして行き来できる成分（ループできなければ単独の点）に分解することを、強連結成分分解と呼びます。
問題: 競プロ典型90問_021: Come Back in One Piece（★5）
N, M = map(int, input().split())
S = [list(map(int, input().split())) for _ in range(M)]
# 有向グラフの典型入力を双方向で適用
from collections import defaultdict
adj, adj_inv = defaultdict(list), defaultdict(list)
for a, b in S:
adj[a-1].append(b-1)
adj_inv[b-1].append(a-1)
# 帰りがけ順を求める（グラフは連結でなくてもよい）
def compute_backward_list():
seen = [False] * N
finished = [False] * N
backward_list = []
for start in range(N):
if seen[start]:
continue
todo = [~start, start]
while todo:
pos = todo.pop() # LIFOでpop
if pos >= 0:
if finished[pos]:
continue
seen[pos] = True
# 行きがけ順の処理
# 次の位置を探索する
for next_ in adj[pos]:
if seen[next_]:
continue
todo.append(~next_) # 帰りがけはビット反転
todo.append(next_)
else:
pos = ~pos # ビット反転を戻す
if finished[pos]:
continue
finished[pos] = True
# 帰りがけ順の処理
backward_list.append(pos)
return backward_list
def dfs(pos, label):
todo = []
todo.append(pos) # 初期探索場所をpush
while todo:
pos = todo.pop() # LIFOでpop
if seen[pos]:
continue
seen[pos] = True
groups[label].append(pos)
# 次の位置を探索する
for next_ in adj_inv[pos]:
todo.append(next_)
return
# Step1: 帰りがけ順（backward_listを作る）
backward_list = compute_backward_list()
# Step2: 帰りがけの逆順でdfsすることでグループを求める
seen = [False] * N
groups = defaultdict(list)
label = 0
for n in reversed(backward_list): # 帰りがけの逆順
if not seen[n]:
dfs(n, label)
label += 1
ans = 0
for k, v in groups.items():
num = len(v)
ans += num * (num - 1) // 2
print(ans)
計算量は$O(N + M)$です。
ベンチマークは、LowLinkと同様のグラフの有向グラフ版で行いました。2つの輪が、それぞれ成分に分解されます。
| N | 10**4 | 10**5 | 10**6 |
|---|---|---|---|
| Python3.8 | 51ms | 332ms | 4030ms |
| PyPy3 | 91ms | 173ms | 1321ms |
3.11. 最大流問題
問題: 競プロ典型90問_040: Get More Money（★7）
最大流問題は、最大フロー問題、最小カット問題、燃やす埋める問題とも言われ、難解ですが、美しく解けるグラフ問題の花形です。高速なDinicのアルゴリズムを実装してみました。
from collections import deque
INF = 10 ** 16
class MfGraph:
def __init__(self, N):
self.N = N
# 辺を列挙するための情報
self.pos = []
# 辺の情報 G[[[to, rev, cap], ...], ...]
self.G = [[] for _ in range(N)]
def add_edge(self, fr, to, cap):
# i番目の辺 = G[pos[i][0]][pos[i][1]] となるようにposをつくる
self.pos.append((fr, len(self.G[fr])))
# 辺をつくる
rev = len(self.G[to]) + (1 if fr == to else 0) # 逆辺 = G[to][rev]
self.G[fr].append([to, rev, cap])
# 逆辺をつくる
rev = len(self.G[fr]) - 1 # 逆辺の逆辺 = 元の辺 = G[fr][rev]
self.G[to].append([fr, rev, 0]) # 容量0
return len(self.pos) - 1
def get_edge(self, i):
e = self.G[self.pos[i][0]][self.pos[i][1]] # i版目の辺
re = self.G[e[0]][e[1]] # 逆辺
# [fr, to, cap, flow]の形で返す
# 逆辺にflowが流れた分だけ元の辺のcapが減る
return [self.pos[i][0], e[0], e[2] + re[2], re[2]]
def edges(self):
return [self.get_edge(i) for i in range(len(self.pos))]
def change_edges(self, i, new_cap, new_flow):
e = self.G[self.pos[i][0]][self.pos[i][1]] # i版目の辺
re = G[e[0]][e[1]] # 逆辺
e.cap = new_cap - new_flow
re.cap = new_flow
def flow(self, s, t, flow_limit=INF):
self.s = s
self.t = t
flow = 0
while flow < flow_limit:
self._bfs(s, t) # sからtへの容量プラスな最短パスを適当に求める
if self.level[t] == -1: # パスが無かったら終了
break
self.it = [0] * self.N
while flow < flow_limit:
# みつかったパスにフローを流せるだけ流し、
# その分、辺の容量を減らし、逆辺の容量を増やす
f = self._dfs(flow_limit - flow)
if f == 0:
break
flow += f
return flow
def min_cut(self, s):
visited = [False] * self.N
visited[s] = True
que = deque()
que.append(s)
while que:
p = que.popleft()
for e in self.G[p]:
if e[2] != 0 and not visited[e[0]]:
visited[e[0]] = True
que.append(e[0])
return visited
def _bfs(self, s, t):
self.level = [-1] * self.N # sから各点への最短距離
self.level[s] = 0
que = deque()
que.append(s)
while que:
v = que.popleft()
for to, _, cap in self.G[v]: # vから出る辺および逆辺を全探索
if cap == 0 or self.level[to] >= 0:
continue # 容量が0の辺、または距離決定済のtoならスキップ
self.level[to] = self.level[v] + 1 # 距離を決定
if to == t: # ゴール到達なら終了
return
que.append(to) # toをキューに乗せる
def _dfs(self, up):
todo = [(self.t, self.it[self.t], up, 0, set())] # (v, i, up, f, seen)
while todo:
v, i, up, f, seen = todo.pop()
# 行きがけ処理
if v == self.s:
d = up
continue
if i >= len(self.G[v]):
self.it[v] = len(self.G[v])
d = f
continue
re = self.G[v][i] # vは終点からスタートするので順方向が逆辺
u, j = re[0], re[1]
e = self.G[u][j] # 逆方向が辺
if i not in seen:
seen.add(i)
self.it[v] = i
if self.level[v] <= self.level[u] or e[2]== 0:
todo.append((v, i + 1, up, f, seen))
continue # u -> v になっていない or 辺の容量が0 ならスキップ
todo.append((v, i, up, f, seen)) # 帰りがけ用に追加
todo.append((u, self.it[u], min(up - f, e[2]), 0, set()))
continue
# 帰りがけ処理
if d > 0:
re[2] += d # 辺の容量を増やす
e[2] -= d # 逆辺の容量を減らす
f += d
if f == up: # 上限に到達したら終了
d = f
continue
todo.append((v, i + 1, up, f, seen))
return f
# 再帰版（未使用）
# sys.setrecursionlimit(10 ** 9)が必要
def _dfs_recursive(self, v, up):
if v == self.s: # 始点・終点が一致したら上限フローが流れる
return up
f = 0
for i in range(self.it[v], len(self.G[v])): # i -> v となるiを探索する
self.it[v] = i # 探索中の位置を更新
re = self.G[v][i] # vは終点からスタートするので順方向が逆辺
u, j = re[0], re[1]
e = self.G[u][j] # 逆方向が辺
if self.level[v] <= self.level[u] or e[2]== 0:
continue # u -> v になっていない or 辺の容量が0 ならスキップ
d = self._dfs_recursive(u, min(up - f, e[2])) # 流せる容量 = min(終点uの解, 現在の辺の容量)
if d <= 0:
continue
re[2] += d # 辺の容量を増やす
e[2] -= d # 逆辺の容量を減らす
f += d
if f == up: # 上限に到達したら終了
return f
self.it[v] = len(self.G[v]) # vは探索終了
return f
N, W = map(int, input().split())
A = list(map(int, input().split()))
S = [list(map(int, input().split())) for _ in range(N)]
# 最大流問題に変換
mf = MfGraph(N + 2)
for n, a in enumerate(A):
mf.add_edge(0, n + 1, W) # 始点0、訪問する費用で結ぶ
mf.add_edge(n + 1, N + 1, a) # 終点N+1、訪問しない費用で結ぶ
for n, s in enumerate(S):
for c in s[1:]:
mf.add_edge(n + 1, c, INF) # 鍵を制約とした短絡路
ans = sum(A) - mf.flow(0, N + 1)
print(ans)
この問題では、計算量は$O(N^4)$です。
ベンチマークは、W=0、全てのA=1として、それぞれの家に、以降の全ての家の鍵かあるパターンで行いました。すべての家に順番に入ることが解答になります。
| N | 500 | 1000 | 2000 |
|---|---|---|---|
| Python3.8 | 309ms | 1747ms | 8116ms |
| PyPy3 | 125ms | 295ms | 1643ms |
Nが大きくなると実行時間が急速に増えています。
3.12. 二部マッチング
問題: 競プロ典型90問_077: Planes on a 2D Plane（★7）
二部マッチングは最大流問題の一種ですが、二部マッチングに特化してDinicよりも定数倍が速いアルゴリズムがあるようです。上記の典型問題は、DinicではTLEしてしまいます。
from collections import deque
class BipartiteMatching:
# https://snuke.hatenablog.com/entry/2019/05/07/013609
def __init__(self, n, m):
self.pre = [-1] * n
self.root = [-1] * n
self.to = [[] for _ in range(n)]
self.p = [-1] * n
self.q = [-1] * m
self.n = n
def add(self, a, b):
self.to[a].append(b)
# マッチング数が返り値に、
# a(n個)から見たマッチ相手がpに入る（マッチしないと-1）
# b(m個)から見たマッチ相手がqに入る（マッチしないと-1）
def solve(self):
res = 0
upd = True
while upd:
upd = False
s = deque()
for i in range(self.n):
if self.p[i] == -1:
self.root[i] = i
s.appendleft(i)
while s:
v = s.pop()
if self.p[self.root[v]] != -1:
continue
for i in range(len(self.to[v])):
u = self.to[v][i]
if self.q[u] == -1:
while u != -1:
self.q[u] = v
self.p[v], u = u, self.p[v]
v = self.pre[v]
upd = True
res += 1
break
u = self.q[u]
if self.pre[u] != -1:
continue
self.pre[u] = v
self.root[u] = self.root[v]
s.appendleft(u)
if upd:
self.pre = [-1] * self.n
self.root = [-1] * self.n
return res
N, T = map(int, input().split())
S = [list(map(int, input().split())) for _ in range(N)]
G = [list(map(int, input().split())) for _ in range(N)]
H = {tuple(t): i for i, t in enumerate(G)}
bm = BipartiteMatching(N, N)
for i, (x, y) in enumerate(S):
H_candiate = [(x + T, y), (x + T, y + T), (x, y + T), (x - T, y + T),
(x - T, y), (x - T, y - T), (x, y - T), (x + T, y - T)]
for (x1, y1) in H_candiate:
if (x1, y1) in H:
j = H[(x1, y1)]
bm.add(i, j)
f = bm.solve()
if f < N:
print('No')
exit()
print('Yes')
ans = bm.p
dir_ = {(T, 0): 1, (T, T): 2, (0, T): 3, (-T, T): 4, (-T, 0): 5, (-T, -T): 6, (0, -T): 7, (T, -T):8}
for fr in range(N):
to = ans[fr]
diff = (G[to][0] - S[fr][0], G[to][1] - S[fr][1])
ans[fr] = dir_[diff]
print(*ans)
この問題では、計算量は$O(N^\frac{3}{2})$です（Dinicでも二部マッチングではこの計算量になります）。
ベンチマークは、各航空機の初期位置をx軸で1ずつずらし、T=1、すべての航空機の方向が同じd=1としています。
| N | 10**4 | 10**5 | 10**6 |
|---|---|---|---|
| Python3.8 | 79ms | 594ms | 7022ms |
| PyPy3 | 123ms | 299ms | 2427ms |
4. 動的計画法
ある問題を、サイズの小さな部分問題に分割して逐次的に解くことで求める解に到達させることを、動的計画法といいます。これまでの探索問題も一種の動的計画法でした。特に、動的計画法と呼ばれる問題の多くは、漸化式をもとに同一の部分問題を再帰的に呼び出します。また、再帰呼び出しの高速化のために、結果をキャッシュしておき2度目以降を省力化する 「メモ化再帰」と呼ばれるテクニックを併用します。
しかしながら、本記事の基本編でも述べている通り、競プロでは再帰をなるべく使わないことが高速化のポイントです。そのため、予め動的計画する空間をリストとして確保しておき、リストの内容を段階的に更新していくことで、回答を求めるようにします。こちらの手法を狭い意味でDPと呼ぶようです。
DPは、複雑な問題になると、「どの順でDPの値リストを埋めていくべきか」を考えて工夫する必要が出てきます。特に多変数の場合、メモ化再帰の場合は、必要な値が再帰的にその場で計算（もしくは計算結果のメモ参照）されるのに対して、DPの場合は、必要な値が予め計算済になっているような計算順序を守ることが肝要です。
メモ化が簡単に記述できるPythonの場合は、順番検討が不要なメモ化再帰の方が簡単に実装できるのですが、性能に課題があるため使えない、という悲しい状態です。
DPを使ったアルゴリズムは、これまでに説明した中でもいくつかありました。
4.1. 動的計画法の基礎
シンプルな動的計画法の問題をもとに、メモ化再帰とDPを比較してみましょう。コードテストからも、「Pythonではメモ化再帰は使えない」という結果になりました。DP一択でがんばりましょう。
問題: 競プロ典型90問_050: Stair Jump（★3）
4.1.1. メモ化再帰
動的計画法の再帰は、ネストが非常に深くなる傾向があるため、再帰の最大数を変更しておくことは必須です。なお、Pythonではメモ化が@lru_cacheの1行ですむため、記述は簡単です。
N, L = map(int, input().split())
MOD = 10 ** 9 + 7
import sys
sys.setrecursionlimit(10 ** 9)
from functools import lru_cache
# dp[階段数] = 通り数、とする
@lru_cache(maxsize=None)
def dp(n):
if n == 0:
return 1
res = dp(n - 1)
if n >= L: # L段以上なら「飛ばし」ができる
res += dp(n - L)
res %= MOD
return res
print(dp(N))
計算量は$O(N)$です。ただし全体的に遅く、意味不明なエラーコードが出てしまっています。なお、code139はスタックオーバーフローとされています。
| N | 10**5 | 10**6 | 10**7 |
|---|---|---|---|
| Python3.8 | 149ms | 1226ms | code139 |
| PyPy3 | 467ms | code30720 | code30720 |
4.1.2. DP
このくらいのシンプルな問題だと、メモ化再帰とDPのコードはほとんど変わりません。
N, L = map(int, input().split())
MOD = 10 ** 9 + 7
# dp[階段数] = 通り数、とする
dp = [0] * (N + 1)
dp[0] = 1
for n in range(1, N + 1):
dp[n] = dp[n - 1]
if n >= L: # L段以上なら「飛ばし」ができる
dp[n] += dp[n - L]
dp[n] %= MOD
print(dp[N])
こちらも計算量は$O(N)$です。メモ化再帰と比較して、とてもよい結果が出ています。
| N | 10**5 | 10**6 | 10**7 |
|---|---|---|---|
| Python3.8 | 74ms | 481ms | 4250ms |
| PyPy3 | 70ms | 79ms | 180ms |
4.2. 部分和
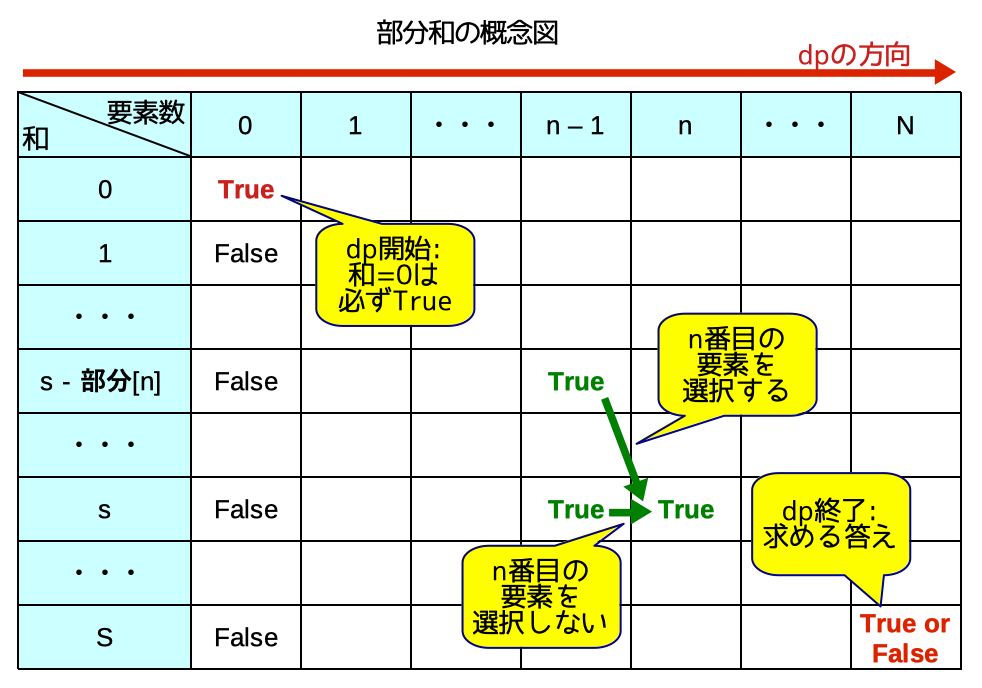
与えられた数値に和が一致する部分列が存在するかどうか、という問題を部分和と呼びます。部分和はdpの一種です。
問題: 競プロ典型90問_056: Lucky Bag（★5）
この問題では、さらに、dp結果を逆順にたどる「dp復元」というテクニックを併用します。
N, S = map(int, input().split())
X = [list(map(int, input().split())) for _ in range(N)]
# 部分和問題に帰着させる前処理
abs_A_sub_B = []
small_A_or_B = []
large_A_or_B = []
for A, B in X:
abs_A_sub_B.append(abs(A - B))
small_A_or_B.append('A' if A <= B else 'B')
large_A_or_B.append('A' if A >= B else 'B')
S -= min(A, B)
if S < 0:
print('Impossible')
exit()
# 部分和問題（dp復元が無ければN方向の履歴は取らなくて良い）
# 部分和として選ばないor選ぶを順に決めていく
# True/Falseではなく通り数を求めることもできる
# dp[n個までの数から選択: 0〜N][和がs: 0〜S]
dp = [[False] * (S + 1) for _ in range(N + 1)] # 通り数の場合は0
dp[0][0] = True # 通り数の場合は1
for n in range(N):
for s in range(S + 1):
dp[n + 1][s] |= dp[n][s] # 選ばない # 通り数の場合は+=
if abs_A_sub_B[n] <= s:
dp[n + 1][s] |= dp[n][s - abs_A_sub_B[n]] # 選ぶ # 通り数の場合は+=
if not dp[N][S]:
print('Impossible')
exit()
# dp復元
ans = []
s = S
for n in reversed(range(N)):
if dp[n][s]:
ans.append(small_A_or_B[n])
else:
ans.append(large_A_or_B[n])
s -= abs_A_sub_B[n]
print(''.join(reversed(ans)))
計算量は$O(N \times S)$です。N = S = 1000くらいの問題が多いです。出題例では、N = 100, S = 100_000 でした。なお、この問題に限り、計算量は、$S := S - \sum min(A_i, B_i)$として計算します。
ベンチマークは、S = N*2として、すべてのA=2, B=1としました。すべてAを選択するのが解答になります。
| N | 1000 | 5000 | 10000 |
|---|---|---|---|
| Python3.8 | 512ms | code9 | code9 |
| PyPy3 | 107ms | 820ms | 3838ms |
4.3. 最長増加部分列（LIS）
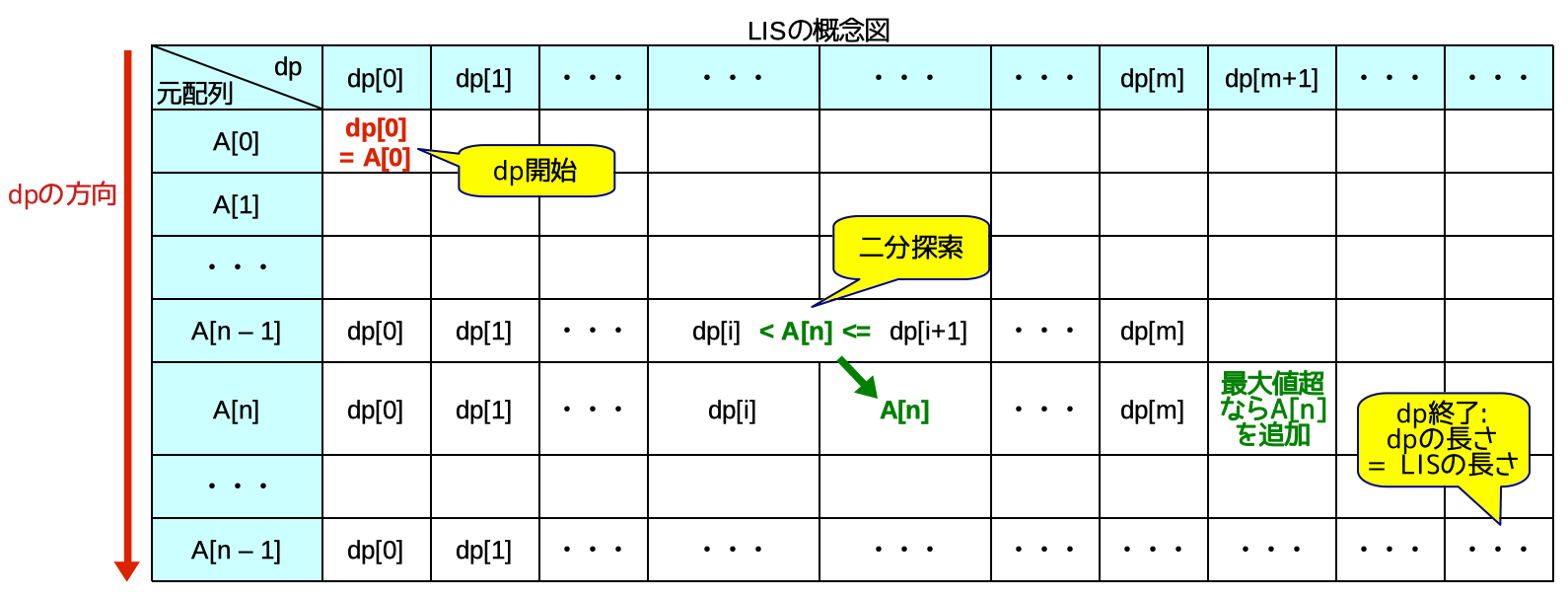
最長増加部分列LISのアルゴリズムはdpの一種です。「増加部分列のm番目の要素になりうる値」をdpで常に更新し続けることで、最長な部分列（の長さ）を求めることができます。
得られる結果は「dpの長さ = LISの長さ」です。dpの中身はLISそのものとは限らないことに、注意してください。LISそのもの（の一例）を求めるには、少し特殊なdp復元が必要です。
- dpの値を更新した時刻と内容を、履歴として取得しておく。
record[更新位置] = [(時刻, 値), (時刻, 値), ..]とするとよい。 - 最終dp配列の最後から出発して、「更新時刻が若返らないように履歴を選択して」配列を遡っていく。
(現在認識している更新時刻, INF)でrecordを二分探索するとよい。
上記の方針で、dp復元を実装例でも記述し、コメントアウトしてあります。
この問題では逆方向からもLISを求めて、結果をあわせて答えを求めます。
N = int(input())
A = list(map(int, input().split()))
INF = 10 ** 16
def lis(A):
dp = []
Q = [] # Qは途中の長さでのLISを求める、本問題特有の要素
#record = [[] for _ in range(N)]
import bisect
for t, a in enumerate(A):
i = bisect.bisect_left(dp, a)
# record[i].append((t, a))
if len(dp) <= i:
dp.append(a)
elif a < dp[i]:
dp[i] = a
Q.append(len(dp))
''' dp復元でLISそのものを求める
res = []
t = N - 1
for n in reversed(range(len(dp))):
i = bisect.bisect_left(record[n], (t, INF)) - 1
t, a = record[n][i]
res.append(a)
return res[::-1]
'''
return Q
lis_ = lis(A)
lis_inv = lis(A[::-1])[::-1]
ans = 0
for a, d in zip(lis_, lis_inv):
ans = max(ans, a + d - 1)
print(ans)
計算量は$O(N \log N)$です。N = 200_000くらいの問題が多いです。出題例では、N = 300_000でした。
ベンチマークは、Aを1から順に1ずつ増えていくリストにして、行いました。
| N | 10**4 | 10**5 | 10**6 |
|---|---|---|---|
| Python3.8 | 32ms | 144ms | 1250ms |
| PyPy3 | 82ms | 105ms | 395ms |
より直感的な解法として、部分列の最後の値を軸としたセグメント木を使って、LISを順次計算する方法があります。
参考: LIS でも大活躍！ DP の配列使いまわしテクニックを特集
def lis(A):
Q = [0] * N
seg = SegmentTree(max, 0, N + 1)
for i, a in enumerate(A):
Q[i] = max(seg.get(a), seg.prod(0, a) + 1)
seg.set(a, Q[i])
return Q
ベンチマークは省略します。若干、定数倍が大きいですが、計算量は $O(N log N)$ です。
4.4. 耳DP
位置のほかに現在の状態をパラメータに持つことで解けるDPを、状態DPまたは耳DPと呼びます。
問題: 競プロ典型90問_008: AtCounter（★4）
この問題の場合、全体文字列の中の探索済み位置のほかに、検索文字列の検索済み位置を状態として持つことで、DPを作ることができます。
N = int(input())
S = input()
match = 'atcoder'
MOD = 10 ** 9 + 7
# dp[i][j] 部分列 S[:i] に部分列 match[:j] が含まれる通り数
dp = [[0] * (len(match) + 1) for _ in range(N + 1)]
for i in range(N + 1):
for j in range(len(match) + 1):
if j == 0:
dp[i][0] = 1
elif i == 0:
dp[0][j] = 0
elif S[i - 1] == match[j - 1]:
dp[i][j] = (dp[i - 1][j] + dp[i - 1][j - 1]) % MOD
else:
dp[i][j] = dp[i - 1][j]
print(dp[N][len(match)])
DPの2次元要素数である状態数:len(match) + 1は定数とみなせるので、計算量は$O(N)$です。N = 100_000くらいの問題が多いです。出題例でも、N = 100_000 でした。
ベンチマークは、文字列atcoderを繰り返して（最後はatcoderの途中まで使って）合計N文字にしたものをSとして、行いました。
| N | 10**4 | 10**5 | 10**6 |
|---|---|---|---|
| Python3.8 | 59ms | 384ms | 4122ms |
| PyPy3 | 117ms | 130ms | 514ms |
4.5. しゃくとり法
ある条件を満たす連続区間の最大長や最小長を求める場合は、しゃくとり法が利用できます。しゃくとり虫のように、区間の右端を伸ばし、左端を縮めながら、条件を満たす全区間を探索します。右端と左端をパラメータに持つ、一種のDPと言えます。
なお、多くの問題は、区間の右端を伸ばす処理を主ループにすると、実装がしやすく高速になるようです。
問題: 競プロ典型90問_034: There are few types of elements（★4）
N, K = map(int, input().split())
A = list(map(int, input().split()))
from collections import defaultdict
count = defaultdict(int)
num_kind = 0
ans = 0
l = 0
for r in range(N): # 閉区間 [l, r]
# 伸ばす処理
if count[A[r]] == 0:
num_kind += 1
count[A[r]] += 1
while num_kind > K:
# 伸び過ぎたので縮む処理
count[A[l]] -= 1
if count[A[l]] == 0:
num_kind -= 1
l += 1
ans = max(ans, r - l + 1)
print(ans)
計算量は$O(N)$です。
本家の典型90の解説では、計算量は$O(N \log N)$となっておりますが、c++の
std::map（$O(\log N)$)を利用しているためです。Pythonのdict（$O(1)$）を利用している上記のコードは$O(N)$になります。
ベンチマークは、K=N/2として、Aを1から順に1ずつ増加するリストにして行いました。
| N | 10**4 | 10**5 | 10**6 |
|---|---|---|---|
| Python3.8 | 36ms | 121ms | 947ms |
| PyPy3 | 91ms | 103ms | 289ms |
4.6. ビットDP
処理途中の状況を集合（=ビット表現で1つの整数）により管理してdp処理をすることを、ビットDPと呼びます。ビット表現をすることにより、部分集合の列挙や、補集合の計算など、さまざまなテクニックが生まれます。
問題: 競プロ典型90問_045: Simple Grouping（★6）
これも
INF = float('inf')にするとTLEします。出題上の最大値を超えて64bit符号付き整数に収まる値である、INF = 1 << 62を使いました。
N, K = map(int, input().split())
S = [list(map(int, input().split())) for _ in range(N)]
# 各点の距離の二乗を求めておく
dist = [[(x1 - x2) ** 2 + (y1 - y2) ** 2 for x1, y1 in S] for x2, y2 in S]
# 最大値 ((10**9) **2) *2 より大きい数で、64ビット符号付き整数の最大値以下の数
# float('inf')を使うとTLEする
INF = 1 << 62
dp0 = [0] * (2 ** N)
# 各部分集合に含まれる点同士の距離最大値をすべて求める = dp初期値
from itertools import combinations
for bit in range(2 ** N): # 部分集合をビット列で表現する
bitset = {i for i in range(N) if bit & (1 << i)}
if len(bitset) >= 2:
dp0[bit] = max([dist[i][j] for i, j in combinations(bitset, 2)])
# dp遷移 dp[k][集合] = min_すべての真部分集合(max(dp[k-1][真部分集合], dp[0][補集合]))
dp = dp0.copy()
for k in range(1, K):
for bit in reversed(range(2 ** N)): # 上から計算するとk方向の履歴が不要
dp[bit] = INF
subbit = bit
while subbit > 0:
dp[bit] = min(dp[bit], max(dp[subbit], dp0[bit - subbit])) # 補集合のテクニック
subbit = (subbit - 1) & bit # 部分集合を列挙するテクニック
print(dp[2 ** N - 1])
bitDP部分の計算量は通常$O(2^N)$で、Kを走査する分と合わせて$O(2^N \times N)$になります。ただし、部分集合の列挙があるため、全体の計算量は$O(3^N \times N)$になっています。出題例では、N = 15になっており、計算すると$3^N \times N = 215,233,605$であるため、実行制限2秒はかなりの難関です。
ベンチマークは、K=N//2として、各点はx軸に等間隔で並べたもの、としました。
| N | 13 | 15 | 17 |
|---|---|---|---|
| Python3.8 | 4034ms | code9 | code9 |
| PyPy3 | 324ms | 463ms | 3404ms |
PythonとPyPyで大きな差があるようです。
ビットDPの応用として、N <= 17程度で、巡回セールスマン問題の厳密解を求めることが可能です。
ABC180E: Traveling Salesman among Aerial Cities
N = int(input())
S = [list(map(int, input().split())) for _ in range(N)]
# 都市間の移動コストを求めておく
dist = [[0] * N for _ in range(N)] # dist[u][v]は、u->vのコスト
for u in range(N):
for v in range(N):
a, b, c = S[u]
p, q, r = S[v]
dist[u][v] = abs(p - a) + abs(q - b) + max(0, r - c)
INF = 10 ** 16
# U:通過済都市のbit、n:現在地として、dp[U][n]=コスト総和
dp = [[INF] * N for _ in range(1 << N)]
dp[0][0] = 0 # 初期状態 = コスト0
for U in range(1 << N):
for u in range(N):
if not (U >> u) & 1 and U > 0: # uは未通過 かつ初期値以外なら、スキップ
continue
for v in range(N):
if (U >> v) & 1: # vは通過済ならスキップ
continue
next_bit = U | (1 << v) # 次にvを通過するbit
dp[next_bit][v] = min(dp[next_bit][v], dp[U][u] + dist[u][v])
print(dp[(1 << N) - 1][0]) # 全て通過済で、最初の都市に戻った状態
計算量は$O(N^2 \times 2^N)$です。ベンチマークは省略します。
4.7. 木DP
木の葉から根に向けてdp処理をすることを、木DPと呼びます。帰りがけ処理を使いますが、木構造を前提にすることで実装は簡単です。
問題: 競プロ典型90問_039: Tree Distance（★5）
N = int(input())
S = [list(map(int, input().split())) for _ in range(N - 1)]
# 無向グラフの典型入力
from collections import defaultdict
adj = defaultdict(list)
for a, b in S:
adj[a-1].append(b-1)
adj[b-1].append(a-1)
# 各頂点の次数と、次数1の頂点（=葉）を開始地点として求める
# 問題によっては、木の根は開始地点にならないことに注意
deg = [0] * N
leafs = []
for k, v in adj.items():
deg[k] = len(v)
if deg[k] == 1:
leafs.append(k)
# 処理用の準備
dp = [0] * N
# 開始地点を起点にdfsで木を探索
seen = [False] * N
while leafs:
pos = leafs.pop()
seen[pos] = True
dp[pos] = sum([dp[x] for x in adj[pos]]) + 1
# ここで処理
for next_ in adj[pos]:
if seen[next_]:
continue
deg[next_] -= 1 # 親ノードの次数を減らしていく
if deg[next_] == 1: # 次数が1になったら親ノードが新たな葉になる
leafs.append(next_)
# 答えを求める
ans = 0
for n in range(N):
ans += (N - dp[n]) * dp[n]
print(ans)
計算量は$O(N)$です。2024/5/12に実装を修正してりおり、以下はそれ以前の計測値です。
| N | 10**4 | 10**5 | 10**6 | |
|---|---|---|---|---|
| バス型 | Python3.8 | 52ms | 274ms | 3140ms |
| PyPy3 | 114ms | 217ms | 876ms | |
| ツリー型 | Python3.8 | 46ms | 272ms | 3004ms |
| PyPy3 | 89ms | 169ms | 1022ms |
4.8. 期待値DP
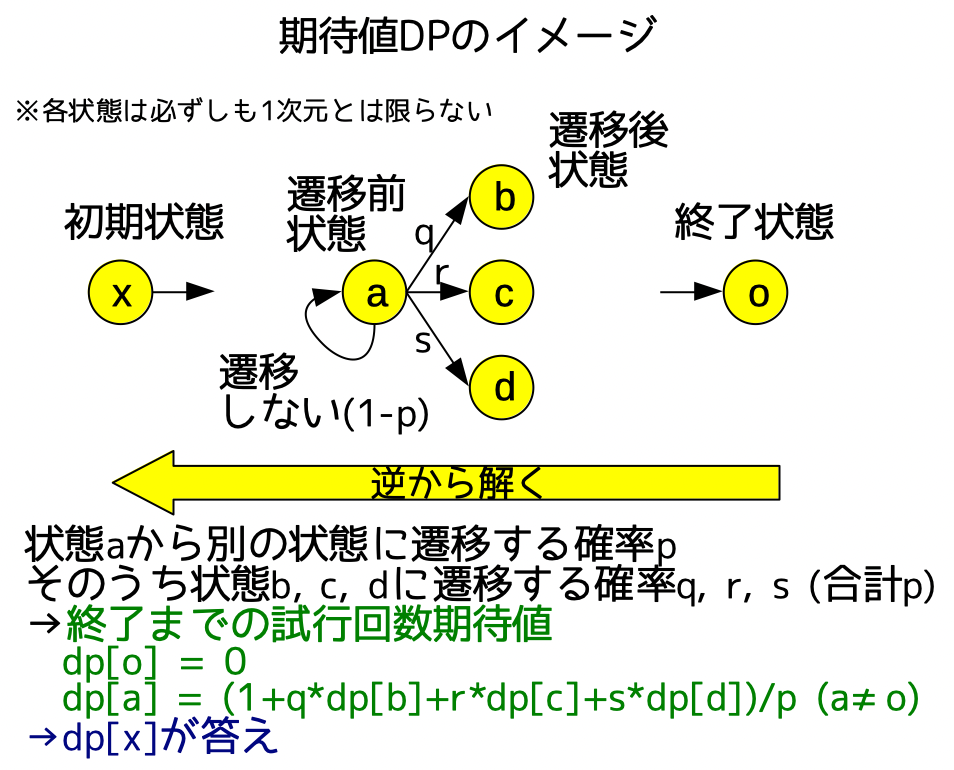
何からの条件下での期待値を求めるdpです。終了方向に向かって確率的に状態遷移していくため、終了状態をdpの起点として、前の状態の期待値=Σ(次の状態の確率×期待値)を逐次に解いていくと、考えやすいです（逆から解く）。
特に、試行回数の期待値を求める例を、以下に示します。
なお、期待値を小数で求めさせる場合と、MODで求めさせる場合があります。後者の場合、冷静に確率計算の分母について、逆元（基本編を参照）をかけてあげれば良いです。デバッグが難しいので、デバッグ時は小数にしたほうがよいでしょう。
また、期待値の線型性などの性質を用いて計算量を激減させ、dpではなく全探索を使う問題もありますので、見極めが必要です。参考:競プロ典型90問_066 - Various Arrays（★5）
N, P = map(int, input().split())
MOD = 998244353
dp = [0] * (N + 1) # dp[n: 残り体力] = 試行数の期待値
INV100 = pow(100, MOD - 2, MOD)
q = P * INV100 % MOD # 体力が2減る確率
r = (1 - P * INV100) % MOD # 体力が1減る確率
# p = 1 # 必ず遷移する
for n in range(1, N + 1):
dp[n] = (1 + q * dp[max(0, n - 2)] + r * dp[n - 1]) % MOD
print(dp[N])
計算量は$O(N)$です。速度測定は省略します。
5. インタラクティブ問題
AtCoderでは、インタラクティブ問題は稀にしか出て来ません。しかしながら、いざ出題されると、逐次に入出力を確認する必要があるため、デバッグが難しいという特性があります。
そのため、提出プログラムとジャッジプログラムが一体となったスニペットを用意しておき、DEBUG定数によってローカルジャッジ（シミュレーション）とオンラインジャッジを切り替えられるようにしておくと、さまざまな入出力パターンを自動で確認することができて、便利です。
問題: 競プロ典型90問_053: Discrete Dowsing（★7）
import os
import sys
import random
DEBUG = False
#DEBUG = os.environ.get('ATCODER', '0') != '1' # 言語Update2023から利用可能
class Judge:
def __init__(self):
self.N = 1500
self.counter = 0
# 条件に合うテストケースを生成
max_pos = random.randint(0, self.N - 1) # 正解の位置
self.max_a = random.randint(self.N, 10 ** 9) # 正解の値
self.A = sorted(random.sample(range(self.max_a - 1), max_pos)) + [self.max_a] + sorted(random.sample(range(self.max_a - 1), self.N - max_pos - 1), reverse=True)
# テストケース数の入力
@classmethod
def input_T(cls):
if DEBUG:
return 50
else:
return int(input())
# 前提条件の入力
def input_params(self):
if DEBUG:
return self.N
else:
return int(input())
# 質問と回答のクエリー
def query(self, n):
self.counter += 1
if DEBUG:
return self.A[n - 1]
else:
print(f'? {n}', flush=True)
return int(input())
# 解答の提出
def submit(self, max_a):
if DEBUG:
print(f'# of queries: {self.counter}', flush=True, file=sys.stderr)
print(f'Submitted {max_a}: {max_a == self.max_a}', flush=True, file=sys.stderr)
else:
print(f'! {max_a}', flush=True)
import bisect
T = Judge.input_T()
for _ in range(T):
J = Judge()
N = J.input_params()
GOLDEN_RATIO = 0.382 # 黄金分割比
q = [1 + int(N * GOLDEN_RATIO)] # 次のクエリー
max_a, max_n = 0, 0 # 最大値とそのインデックス
history = [] # 検索済みインデックス（bisectで常時ソート）
while len(q) > 0:
# クエリーを1つ実行
n = q.pop()
a = J.query(n)
bisect.insort_left(history, n)
# 最大値を更新
if max_a < a:
max_a = a
max_n = n
# 最大値のインデックスの隣接半開区間[l, n) [n, r)を求める
i = bisect.bisect_right(history, max_n)
j = bisect.bisect_left(history, max_n) - 1
r = history[i] if i < len(history) else N + 1
l = history[j] if j >= 0 else 0
# 広い方の隣接半開区間について黄金分割した位置を、クエリーに加える
if r - max_n < max_n - l:
if l + 1 < max_n:
q.append(max_n - int(1 + (max_n - l - 2) * GOLDEN_RATIO))
else:
if max_n + 1 < r:
q.append(max_n + int(1 + (r - max_n - 2) * GOLDEN_RATIO))
J.submit(max_a)
インタラクティブ問題の制限時間は、テストプログラムと提出プログラムの合計となるため、速度測定は省略します。