0. はじめに
動的計画法の解法に対しては、「一次元 DP」や「二次元 DP」といった呼称でよびたくなりがちです。たとえば
- ${\rm dp}[i] := i$ 番目の地点まで到達するまでの最小コスト
というような DP テーブルを用いるような DP1 は一次元 DP であり、
- ${\rm dp}[i][w] := N$ 個の品物のうち最初の $i$ 個の品物の中から、重さが $w$ を超えない範囲でいくつか選んだときの、選んだ品物の価値の総和の最大値
というような DP テーブルを用いるような DP2 は二次元 DP である、といった具合です。後者はいわゆるナップサック問題に対する DP として有名ですね!
二次元 DP の配列を再利用して一次元へ
しかし今回は、DP を一次元や二次元とよぶことにあまり意味がないかもしれない...という話をします。たとえばナップサック DP は、なんと実は、一次元配列で実現できてしまうのです!
- ${\rm dp}_{i}[w] := N$ 個の品物のうち最初の $i$ 個の品物の中から、重さが $w$ を超えない範囲でいくつか選んだときの、選んだ品物の価値の総和の最大値
という感じです。こうすることでメモリ使用を大幅に効率化することができます。AtCoder ではメモリ制約が厳しい場面は多くないですが、昔は topcoder などではこの手の配列使いまわしテクニックを要求する問題も多く見られました。そしてこのテクニックは、時には、単なるメモリ節約になるだけでなく、根本的に計算量改善につながるケースもあるのです!実はおなじみの LIS (Longest Increasing Subsequence、最長増加部分列問題) も、そのようなケースとなっています。
本記事では、その周辺の事柄をまとめます。なおこの記事は、koba-e964 さんの問題提起をきっかけとして生まれました。
目次
- ナップサック DP
- 個数制限なしナップサックの場合
- LIS の解法(1) (二分探索 ver.)
- LIS の解法(2) (セグ木 ver.)
- EDPC Q - Flowers
- インライン DP、とくに EDPC W - Intervals
最初にナップサックの話をしてから、LIS (最長増加部分列問題) に入る構成となっています。しかしながら、ナップサックの話と、LIS の話は独立しています。LIS に関心のある方はナップサックを飛ばして、いきなり LIS に入ってもらえたらと思います。
1. ナップサック DP
ナップサック問題に対する DP を簡単に復習しておきましょう。初見の方は先に以下の記事を読んでもらえたらと思います。
ナップサック問題は以下のような問題でした。
問題概要
$N$ 個の品物があり、$i$ 番目の品物のそれぞれ重さと価値が $\rm{weight}[i], \rm{value}[i]$ で与えられます ($i = 0, 1, ..., N-1$)。
これらの品物から重さの総和が $W$ を超えないように選んだときの、価値の総和の最大値を求めてください。
【数値例】
- $N = 4$
- $W = 6$
- $(\rm{weight},\rm{value}) = {(3, 6), (1, 3), (2, 1), (4, 85)}$
答え: $88 ((1, 3), (4, 85)$ を選んだときが最大です)
解法 (通常)
ナップサック問題は以下のようなテーブルを設計することで解くことができるのでした。
- ${\rm dp}[i][w] := N$ 個の品物のうち最初の $i$ 個について、重さの総和が $w$ 以下となるようにいくつか選んだときの、選んだ品物の価値の総和の最大値
そして、DP の更新式は以下のようになります。
- ${\rm chmax}({\rm dp}[i + 1][w], {\rm dp}[i][w]) (i$ 番目の品物を選ばない場合)
- ${\rm chmax}({\rm dp}[i + 1][w], {\rm dp}[i][w-{\rm weight}[i]] + {\rm value}[i]) (i$ 番目の品物を選ぶ場合)
ここで chmax(a, b) 関数は、以下のコードのように、a と b とを比較して、a よりも b の方が大きい場合には a を b に更新する関数です。a という「暫定王者」に対して b という「チャレンジャー」が現れて、b の方が a よりも大きかったら b の値が新たに王者となるイメージです。
template<class T> inline void chmax(T& a, T b) {
if (a < b) a = b;
}
ナップサック DP を実装すると、以下のコードのようになります。これは Educational DP Contest D - Knapsack 1 に準拠したものになっています。
# include <iostream>
# include <vector>
using namespace std;
template<class T> void chmax(T &a, T b) {
if (a < b) a = b;
}
int main() {
int N, W;
cin >> N >> W;
vector<int> weight(N), value(N);
for (int i = 0; i < N; ++i) cin >> weight[i] >> value[i];
vector<vector<long long>> dp(N+1, vector<long long>(W+1, 0));
for (int i = 0; i < N; ++i) {
for (int w = 0; w <= W; ++w) {
chmax(dp[i+1][w], dp[i][w]);
if (w - weight[i] >= 0) {
chmax(dp[i+1][w], dp[i][w - weight[i]] + value[i]);
}
}
}
cout << dp[N][W] << endl;
}
ナップサック DP を in-place 化
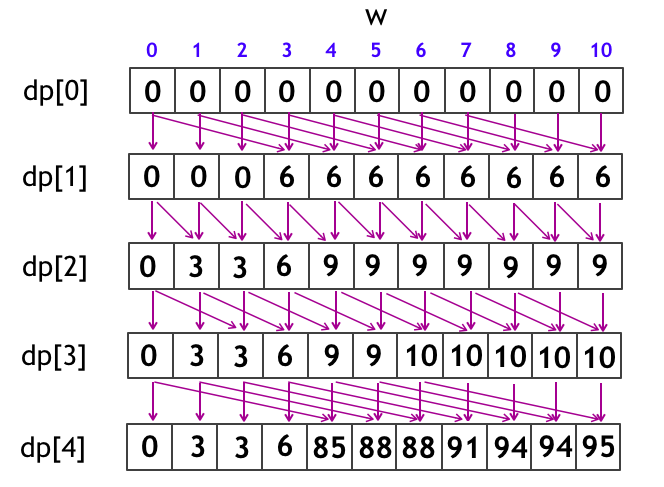
さて、上記のナップサック DP は、下図のように更新をしていっています。数値例に挙げた
- $N = 4$
- $W = 6$
- $(\rm{weight},\rm{value}) = {(3, 6), (1, 3), (2, 1), (4, 85)}$
の場合を示しています。
このように通常のナップサック DP では、各配列 ${\rm dp}[0], {\rm dp}[1], {\rm dp}[2], \dots, {\rm dp}[N]$ の各値をすべて残しています。つまり、$O(NW)$ だけのメモリ量を要しています。しかしよく考えてみると、これは大きな無駄をしています。
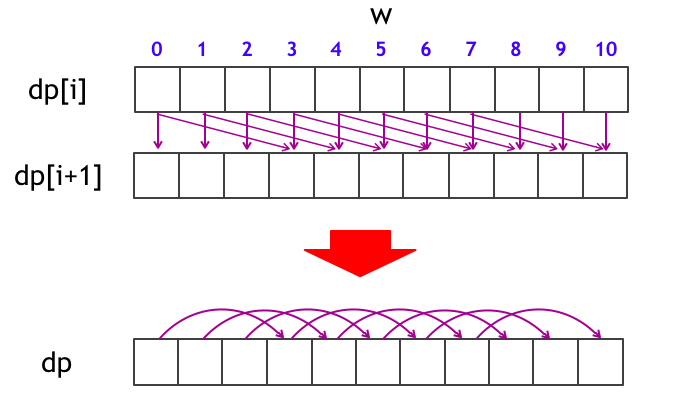
${\rm dp}[0], {\rm dp}[1], {\rm dp}[2], \dots, {\rm dp}[N]$ をすべて同じ配列で使い回すことを考えてみましょう。下図のようなイメージです。
まず注目したいこととして、DP 配列を毎回使い回すのならば、
- ${\rm chmax}({\rm dp}[i + 1][w], {\rm dp}[i][w]) (i$ 番目の品物を選ばない場合)
- ${\rm chmax}({\rm dp}[i + 1][w + {\rm weight}[i]], {\rm dp}[i][w] + {\rm value}[i]) (i$ 番目の品物を選ぶ場合)
という 2 つの更新式のうち、前半については特に何もしなくてよいことがわかります。後半についてはイメージ的に言えば
- ${\rm chmax}({\rm dp}[w + {\rm weight}[i]], {\rm dp}[w] + {\rm value}[i])$
という感じの更新をしたいです。そこで、以下のコードのようにしたらどうでしょうか...
vector<long long> dp(W+1, 0);
for (int i = 0; i < N; ++i) {
for (int w = 0; w <= W; ++w) {
if (w - weight[i] >= 0) {
chmax(dp[w], dp[w - weight[i]] + value[i]);
}
}
}
しかしこれではうまく行きません。なぜなら、このままでは、 ${\rm dp}[w]$ を更新するために用いる ${\rm dp}[w - {\rm weight}[i] ]$ の値は、すでに ${\rm dp}[w - 2\times{\rm weight}[ i ] ]$ を用いて更新されている...みたいな状態になっているからです。
${\rm dp}[w]$ の更新に用いる ${\rm dp}[w - {\rm weight}[i] ]$ の値は、更新前のものでなければなりません。なお、後述しますが、実はこの失敗例の DP もそれなりに意味のあるものにはなっています。具体的には次章で見る個数制限なしナップサック問題を解くコードになっています。
さて、${\rm dp}[w]$ を更新するために用いる ${\rm dp}[w - {\rm weight}[i] ]$ の値がすでに更新済であることが問題なのでした。そこで DP ループのうちの for (int w = 0; w <= W; ++w) の部分の添字 w を逆から回してみましょう。
vector<long long> dp(W+1, 0);
for (int i = 0; i < N; ++i) {
for (int w = W; w >= 0; --w) {
if (w - weight[i] >= 0) {
chmax(dp[w], dp[w - weight[i]] + value[i]);
}
}
}
実はたったこれだけの工夫により、上手く行きます!
今度は、${\rm dp}[w]$ の値を ${\rm dp}[w - {\rm weight}[i] ]$ を用いて更新するとき、${\rm dp}[w - {\rm weight}[i] ]$ の値は更新前のものになります。まとめると以下のコードによって、Educational DP Contest D - Knapsack 1 から AC をとれます!計算量は $O(NW)$ で変わりません。
# include <iostream>
# include <vector>
using namespace std;
template<class T> void chmax(T &a, T b) {
if (a < b) a = b;
}
int main() {
int N, W;
cin >> N >> W;
vector<int> weight(N), value(N);
for (int i = 0; i < N; ++i) cin >> weight[i] >> value[i];
vector<long long> dp(W+1, 0);
for (int i = 0; i < N; ++i) {
for (int w = W; w >= 0; --w) {
if (w - weight[i] >= 0) {
chmax(dp[w], dp[w - weight[i]] + value[i]);
}
}
}
cout << dp[W] << endl;
}
注意点(1): 上手く行く場合と、ダメな場合
競プロで登場する DP の 8 割は、以下のような感じの DP だと思います。
- ${\rm dp}[i][j] := N$ 個のうちの最初の $i$ 個について、状態が $j$ であるような場合についての最適値
という DP テーブルに対して、
- ${\rm chmax}({\rm dp}[i+1][k], {\rm dp}[i][j]$ + (何か))
というような更新式で更新していくような DP です。このような「左から順にシーケンシャルに見ていくような DP」では、最初の添字 $i$ をつぶして配列使いまわしができる可能性があります。しかし常に上手くいくわけではありません。上手く行く十分条件として、以下のものがあります。
${\rm dp}[i][j]$ から ${\rm dp}[i+1][k]$ への遷移において、常に $k > j$ となっているとき
ナップサック DP はこの条件を満たします。この条件を満たしていれば、
for (int k = W; k >= 0; --k) {
int j = k - (何か); // k に遷移する元
chmax(dp[k], dp[j] + (何か));
}
for (int j = W; j >= 0; --j) {
int k = j + (何か); // j から遷移する相手
chmax(dp[k], dp[j] + (何か));
}
という風に配列を使いまわしながら更新式を書いても、更新元の ${\rm dp}[j]$ の値が更新される前に ${\rm dp}[k]$ の更新を行うことができます。添字はやはり逆から回すことに注意します。
注意点(2): より汎用的に使える、メモリ節約テクニック
シーケンシャルな DP に対して、もう少し汎用的に使えるメモリ節約テクニックもあります。上述の DP は、
- 「更新前」と「更新後」も同じ配列
でした。それをたとえば
- 「更新前」の配列は
dpとする - 「更新後」の配列は
nexとする
というようにし、更新前後の配列を別にします。更新後には dp と nex とを swap するようにします。
ナップサック DP の場合は以下のように実装できます。メモリ容量は $O(W)$ となります。計算量は $O(NW)$ で変わりません。
# include <iostream>
# include <vector>
using namespace std;
template<class T> void chmax(T &a, T b) {
if (a < b) a = b;
}
int main() {
int N, W;
cin >> N >> W;
vector<int> weight(N), value(N);
for (int i = 0; i < N; ++i) {
cin >> weight[i] >> value[i];
}
// dp 配列
vector<long long> dp(W + 1, 0);
// ループ
for (int i = 0; i < N; ++i) {
// 更新後の配列を用意する
vector<long long> nex(W + 1, 0);
// DP の 1 ステップ
for (int w = 0; w <= W; ++w) {
chmax(nex[w], dp[w]);
if (w + weight[i] <= W) {
chmax(nex[w + weight[i]], dp[w] + value[i]);
}
}
// dp と nex を swap する
swap(dp, nex);
}
// 答え
cout << dp[W] << endl;
}
2. 個数制限なしナップサックの場合
次に個数制限なしバージョンのナップサックについても見てみましょう。次のような、同じ品物を何個でも採用してよい、という場合です。
問題概要
$N$ 個の品物があり、$i$ 番目の品物のそれぞれ重さと価値が $\rm{weight}[i], \rm{value}[i]$ で与えられます $(i = 0, 1, ..., N-1)$。
これらの品物から重さの総和が $W$ を超えないように選んだときの、価値の総和の最大値を求めてください。ただし、同じ種類の品物を何個でも選んでもよいものとします。
【数値例】
- $N = 3$
- $W = 7$
- $(\rm{weight},\rm{value}) = {(3, 4), (4, 5), (2, 3)}$
答え: $10 ((3, 4)$ を 1 個、$(2, 3)$ を 2 個選んだときが最大です)
解法
個数制限なしナップサックは、独特な遷移をします。DP テーブルの作り方自体は特に変わりません。
- ${\rm dp}[i][w] := N$ 種類の品物のうち最初の $i$ 種類について、重さの総和が $w$ 以下となるようにいくつか選んだときの、選んだ品物の価値の総和の最大値
そして、 ${\rm dp}[i+1][w]$ の値を考える上で、以下のように場合分けして考えます:
【 $i$ 種類目の品物は 1 個も採用しない場合】
この場合は、${\rm dp}[i][w]$ と変わらないので
- ${\rm chmax}({\rm dp}[i + 1][w], {\rm dp}[i][w])$
となります。これは 0-1 の場合と同じです。
【 $i$ 種類目の品物は 1 個以上採用する場合】
まずは $i$ 種類目の品物を 1 個採用してしまうことにします。1 個採用することで、$i$ 番目の品物を採用してもしなくても良い状態となるので、残りの場合の値は、${\rm dp}[i+1][w- {\rm weight}[i] ]$ となります。よって
- ${\rm chmax}({\rm dp}[i + 1][w], {\rm dp}[i + 1][w- {\rm weight}[i] ] + {\rm value}[i])$
となります。なお、0-1 ナップサックの場合は
- ${\rm chmax}({\rm dp}[i + 1][w], {\rm dp}[i][w- {\rm weight}[i] ] + {\rm value}[i])$
という遷移式でした。ほんの少し違うだけですね。
そして個数制限なしの場合の式を in-place 化するとなると、実は、先ほど失敗例として挙げたコードがドンピシャであることがわかります。今度は、${\rm dp}[w]$ の値を ${\rm dp}[w - {\rm weight}[i] ]$ を用いて更新するとき、${\rm dp}[w - {\rm weight}[i] ]$ の値は更新済みであるべきなんですね。
vector<long long> dp(W+1, 0);
for (int i = 0; i < N; ++i) {
for (int w = 0; w <= W; ++w) {
if (w - weight[i] >= 0) {
chmax(dp[w], dp[w - weight[i]] + value[i]);
}
}
}
3. LIS の解法(1) (二分探索 ver.)
LIS (最長増加部分列問題) は DP の例として超有名問題です。
LIS の解法は、有名なものが 2 種類ありますが、まずは蟻本にも載っている方法を紹介します。この方法は初見だと頭が良すぎるので、「こんなのは知らなきゃ解けない、覚えるしかない」と思われがちです。しかし、LIS も元々は二次元 DP であって、in-place な更新をすることで高速化を達成できたものとしてとらえると、案外自然なものであることがわかります。
問題概要 (LIS)
長さ $N$ の数列 $a_0, a_1, \dots, a_{N-1}$ が与えられます。この数列の部分列であって、単調増加であるようなものの最長の長さを答えてください。
制約
- $1 \le N \le 10^5$
- $0 \le a[i] \le 10^9$
考え方
まずは $O(N^2)$ でもよいから、動的計画法で解けないかを考えてみましょう。最初は素朴に考えると、こんな DP を考えたくなると思います。
- ${\rm dp}[i][j] :=$ 最初の $i$ 項のみを考えた場合の単調増加な部分列であって、最後の要素が $a_j$ であるような場合についての、最長の長さ
とします3。$i$ から $i+1$ への DP の更新は、以下のように書けます
- ${\rm chmax}({\rm dp}[i+1][j], {\rm dp}[i][j]) (a_i$ を選ばない場合)
- ${\rm chmax}({\rm dp}[i+1][i], {\rm dp}[i][j] + 1) (a_i$ を選ぶ場合、ただし $a_i > a_j$ の場合に限る)
この DP 解法は $O(N^2)$ の計算量となります。
添字と値の入れ替え
DP を効率化する上で一つ検討したいこととして「添字と値を入れ替える」というテクニックがあります。そのような顕著な例としては
を読んでいただけたらと思うのですが、ナップサックの場合は、通常
- ${\rm dp}[i][w] := N$ 個の品物のうち最初の $i$ 個について、重さの総和が $w$ 以下となるようにいくつか選んだときの、選んだ品物の価値の総和の最大値
としているところを、以下のようにします。
- ${\rm dp}[i][v] := N$ 個の品物のうち最初の $i$ 個について、価値の総和が $v$ 以上となるようにいくつか選んだときの、選んだ品物の重さの総和の最小値
そして、${\rm dp}[i][v]$ の値が $W$ 以下となるような最大の $v$ が答えとなります。このテクニックは、「ナップサックの容量 $W$ が大きすぎて $O(NW)$ の解法では間に合わないが、各品物の価値が小さい」という場合には大変有効です。
さきほどの LIS に対しても、この「添字と値の入れ替え」を適用してみましょう。そうすると、次のような DP になります。
- ${\rm dp}[i][k] :=$ 最初の $i$ 項のみを考えた場合の単調増加な部分列であって、長さ $k$ であるようなもののうち、その最後の要素の最小値
DP の更新は以下のように考えられるでしょう。$i$ から $i+1$ への更新を考えます。なお、${\rm dp}[i][k]$ は、明らかに $k$ に対して単調増加であることに注意しましょう。
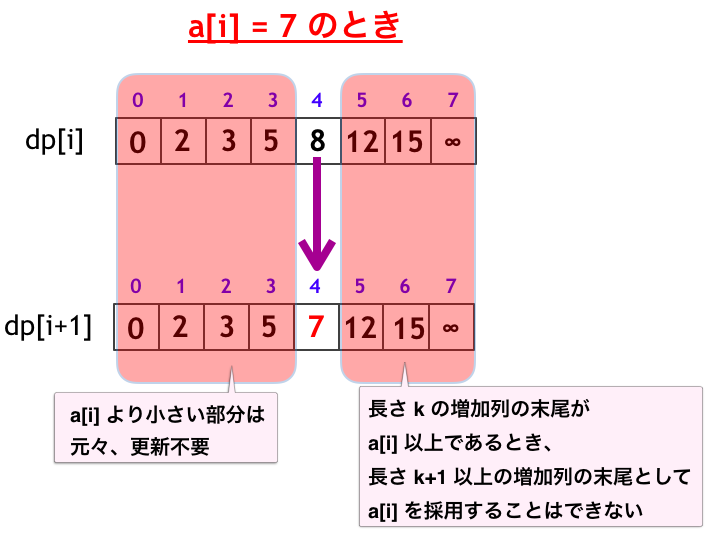
上図の例は、数列のうち最初の $i$ 項のみを考えた場合の ${\rm dp}[i]$ の値が { $0, 2, 3, 5, 8, 12, 15, \infty, \dots$ } であるときに、$a_i = 7$ が舞い込んでくる状況を想定しています。このとき、
- ${\rm dp}[0], {\rm dp}[1], {\rm dp}[2], {\rm dp}[3]$ の値は元々 $a_i = 7$ より小さいので、更新する必要はありません。
- ${\rm dp}[4] = 8$ なので、長さ $4$ の増加列の末尾は必ず $8$ 以上です。よって、長さ $5$ 以上の増加列の末尾として $a_i = 7$ を採用することはできません。
- ${\rm dp}[4]$ の値のみを $a_i = 7$ に更新することができます。
以上の考察を一般化すると、実は、配列 ${\rm dp}[i]$ から配列 ${\rm dp}[i+1]$ へと更新するとき、更新が起きる場所は 1 箇所だけなのです!!!具体的には以下のようになります。
${\rm dp}[i][k] \ge a_i$ となる最小の $k$ についてのみ、
- ${\rm dp}[i+1][k] = a_i$
と更新する。それ以外は更新が起きない。
in-place 化する
上記の DP は「一箇所だけ更新が発生する」「それ以外は更新されない」というものでした。これはもう、in-place 化するしかありません!!!!!
in-place 化することで、${\rm dp}[i+1][j] = {\rm dp}[i][j]$ であるような $j$ については値をコピーする必要がなくなるのです。
そして、${\rm dp}[i][k] \ge a_i$ となる最小の $k$ は、二分探索によって $O(\log{N})$ で求めることができます。つまり $i$ から $i+1$ への更新が $O(\log{N})$ で実現できるのです。よって全体の計算量も $O(N\log{N})$ となります。
以下のコードのように実装できます。これは AOJ Course DPL_1_D: Longest Increasing Subsequence に対して AC がとれるものになっています。また実装上は、ここまで
- ${\rm dp}_i[k] :=$ 最初の $i$ 項のみを考えた場合の単調増加な部分列であって、長さ $k$ であるようなもののうち、その最後の要素の最小値
としていたところを、
- ${\rm dp}_i[k] :=$ 最初の $i$ 項のみを考えた場合の単調増加な部分列であって、長さ $k+1$ であるようなもののうち、その最後の要素の最小値
としています。
# include <iostream>
# include <vector>
# include <algorithm>
using namespace std;
const long long INF = 1LL<<60;
// 最長増加部分列の長さを求める
int LIS(const vector<long long> &a) {
int N = (int)a.size();
vector<long long> dp(N, INF);
for (int i = 0; i < N; ++i) {
// dp[k] >= a[i] となる最小のイテレータを見つける
auto it = lower_bound(dp.begin(), dp.end(), a[i]);
// そこを a[i] で書き換える
*it = a[i];
}
// dp[k] < INF となる最大の k に対して k+1 が答え
// それは dp[k] >= INF となる最小の k に一致する
return lower_bound(dp.begin(), dp.end(), INF) - dp.begin();
}
int main() {
int N; cin >> N;
vector<long long> a(N);
for (int i = 0; i < N; ++i) cin >> a[i];
cout << LIS(a) << endl;
}
4. LIS の解法(2) (セグ木 ver.)
先ほどの LIS の解法は結構天才的でした。特に「添字と値を入れ替える」というのが非自明な感じです。しかし実は、そんなことしなくても、座標圧縮とセグメント木を用いた in-place DP で解くことができます!こっちはかなり自然な解法です。まずは、添字入れ替えテクニックを用いる前の DP を思い出します。
- ${\rm dp}[i][j] :=$ 最初の $i$ 項のみを考えた場合の単調増加な部分列であって、最後の要素が $a_j$ であるような場合についての、最長の長さ
このままだと更新式がカオスなので、少し変えます:
- ${\rm dp}[i][h] :=$ 最初の $i$ 項のみを考えた場合の単調増加な部分列であって、最後の要素が $h$ であるような場合についての、最長の長さ
しかし、これでは $h$ の値が最悪で $10^9$ まで取りうるので破綻してしまいます。そこで座標圧縮とよばれるテクニックを用います。
座標圧縮する
座標圧縮とは、たとえば
1333, 2020, 64, 1, 2020, 514, 11111
といった数列に対して、各項が小さい順に何番目なのかを表すものに変換する手法です。上の例では、以下のようになります (ここでは 1-indexed にしています)。
4, 5, 2, 1, 5, 3, 6
数列を座標圧縮した値に換えても、LIS の答えは変わらないことに注意しましょう!!!重複する数値があっても問題ありません。座標圧縮の詳しいやり方は、以下の記事に書きました。
改めて DP
in-place 化したことで、数列 $a_i$ の各項は $1 \le a_i \le N$ となります。改めて以下の DP を考えてみましょう。
- ${\rm dp}[i][h] :=$ 最初の $i$ 項のみを考えた場合の単調増加な部分列であって、最後の要素が $h$ であるような場合についての、最長の長さ
これを用いると、以下のように更新することができます。
- $h == a[i]$ のとき、${\rm chmax}({\rm dp}[i+1][h], \max_{0 \le k < h} {\rm dp}[i][k] + 1)$
- それ以外のとき、${\rm dp}[i+1][h] = {\rm dp}[i][h]$
in-place 化してセグメント木に載せる
配列 ${\rm dp}[i]$ から配列 ${\rm dp}[i+1]$ への更新が一箇所のみで起きていることから、in-place 化できそうです。in-place 化します。すると、以下のような更新を行えばよいことがわかります。
- $A = \max_{0 \le k < a[i]} {\rm dp}[k]$ として、
- ${\rm chmax}({\rm dp}[a[i]], A + 1)$ と更新する
これはまさにセグメント木適性の高い操作です!
何も工夫をしないと、$A$ を求める部分に探索が必要で、結局 1 回の更新に $O(N)$ の計算量がかかってしまい、全体として $O(N^2)$ の計算量を要します。しかしセグメント木を用いることで、$A$ を $O(\log{N})$ で高速に求めることができます (その代わり、${\rm dp}[a[i]]$ を更新する部分にも $O(\log{N})$ の計算量を要します)。セグメント木は、以下のことができます4。
【セグメント木】
数列 $d_0, d_1, \dots, d_{N-1}$ に対して、以下のクエリにそれぞれ $O(\log{N})$ で答えます:
- 取得クエリ ($l, r$): 数列の区間 $[l, r)$ の最大値を答えます。つまり、$\max(d_l, d_{l+1}, \dots, d_{r-1})$ の値を答えます。
- 更新クエリ ($k, v$): $d_k$ の値を $v$ に書き換えます。
セグメント木の実現方法については、つたじぇー⭐︎さんの以下の記事などを読んでもらえたらと思います。
セグメント木を用いると、LIS は以下のコードで解くことができます。計算量は $O(N\log{N})$ となります。
# include <iostream>
# include <vector>
# include <algorithm>
# include <functional>
using namespace std;
// 抽象化したセグメント木
template<class Monoid> struct SegTree {
using Func = function<Monoid(Monoid, Monoid)>;
const Func F;
const Monoid UNITY;
int SIZE_R;
vector<Monoid> dat;
SegTree(int n, const Func f, const Monoid &unity): F(f), UNITY(unity) { init(n); }
void init(int n) {
SIZE_R = 1;
while (SIZE_R < n) SIZE_R *= 2;
dat.assign(SIZE_R * 2, UNITY);
}
/* set, a is 0-indexed */
void set(int a, const Monoid &v) { dat[a + SIZE_R] = v; }
void build() {
for (int k = SIZE_R - 1; k > 0; --k)
dat[k] = F(dat[k*2], dat[k*2+1]);
}
/* update a, a is 0-indexed */
void update(int a, const Monoid &v) {
int k = a + SIZE_R;
dat[k] = v;
while (k >>= 1) dat[k] = F(dat[k*2], dat[k*2+1]);
}
/* get [a, b), a and b are 0-indexed */
Monoid get(int a, int b) {
Monoid vleft = UNITY, vright = UNITY;
for (int left = a + SIZE_R, right = b + SIZE_R; left < right; left >>= 1, right >>= 1) {
if (left & 1) vleft = F(vleft, dat[left++]);
if (right & 1) vright = F(dat[--right], vright);
}
return F(vleft, vright);
}
inline Monoid operator [] (int a) { return dat[a + SIZE_R]; }
/* debug */
void print() {
for (int i = 0; i < SIZE_R; ++i) {
cout << (*this)[i];
if (i != SIZE_R-1) cout << ",";
}
cout << endl;
}
};
// 最長増加部分列の長さを求める
int LIS(const vector<long long> &a) {
int N = (int)a.size();
// 座標圧縮
vector<long long> aval;
for (int i = 0; i < N; ++i) aval.push_back(a[i]);
sort(aval.begin(), aval.end());
aval.erase(unique(aval.begin(), aval.end()), aval.end());
// セグメント木 (区間取得を max としたもの)
SegTree<int> dp(N+1,
[](int a, int b) { return max(a, b); },
0);
// 更新
int res = 0;
for (int i = 0; i < N; ++i) {
// a[i] が何番目か
int h = lower_bound(aval.begin(), aval.end(), a[i]) - aval.begin();
++h; // 1-indexed にする
// 値取得
int A = dp.get(0, h);
// 更新
if (dp.get(h, h+1) < A + 1) {
dp.update(h, A + 1);
res = max(res, A + 1);
}
}
return res;
}
int main() {
int N; cin >> N;
vector<long long> a(N);
for (int i = 0; i < N; ++i) cin >> a[i];
cout << LIS(a) << endl;
}
5. EDPC Q - Flowers
それでは、LIS を少し応用した問題を解いてみましょう!
Educational DP Contest Q - Flowers です!!!
LIS の別解 (セグメント木を用いた解法) を素直に拡張することで解くことができます。
問題概要
$N$ 本の花が横一列に並んでいます。
左から $i$ 番目の花の高さは $h_i$ で、美しさは $a_i$ です。
太郎君は何本かの花を抜き去ることで、次の条件が成り立つようにしようとしています。
- 残った花を左から順に見ると、高さが単調増加になっている。
残った花の美しさの総和の最大値を求めてください。
制約
- $1 \le N \le 2 \times 10^5$
- $1 \le h_i \le N$
- $h_0, h_1, \dots, h_{N-1}$ はすべて相異なる
考え方
重み付き LIS とでもいうべき問題ですね。LIS (の別解) と同様に、次のような DP を考えてみましょう。
- ${\rm dp}[i][h] :=$ 最初の $i$ 個の花のみを考えた場合の単調増加な花列であって、最後の高さが $h$ であるような場合についての、美しさの総和の最大値
なお、今回は、$1 \le h_i \le N$ という制約があるため、座標圧縮が不要であることに注意しましょう。DP の更新は、
- $h == h_i$ のとき、 ${\rm chmax}({\rm dp}[i+1][h], \max_{0 \le k < h} {\rm dp}[i][k] + a_i)$
- それ以外のとき、${\rm dp}[i+1][h] = {\rm dp}[i][h]$
これを in-place にすると、次のようになります。
- $A = \max_{0 \le k < h[i]} {\rm dp}[k]$ として、
- ${\rm chmax}({\rm dp}[h[i]], A + a_i)$ と更新する
やはりセグメント木を用いて、次のコードのように書けます。計算量は $O(N\log{N})$ となります。
# include <iostream>
# include <vector>
# include <algorithm>
# include <functional>
using namespace std;
// 抽象化したセグメント木
template<class Monoid> struct SegTree {
using Func = function<Monoid(Monoid, Monoid)>;
const Func F;
const Monoid UNITY;
int SIZE_R;
vector<Monoid> dat;
SegTree(int n, const Func f, const Monoid &unity): F(f), UNITY(unity) { init(n); }
void init(int n) {
SIZE_R = 1;
while (SIZE_R < n) SIZE_R *= 2;
dat.assign(SIZE_R * 2, UNITY);
}
/* set, a is 0-indexed */
void set(int a, const Monoid &v) { dat[a + SIZE_R] = v; }
void build() {
for (int k = SIZE_R - 1; k > 0; --k)
dat[k] = F(dat[k*2], dat[k*2+1]);
}
/* update a, a is 0-indexed */
void update(int a, const Monoid &v) {
int k = a + SIZE_R;
dat[k] = v;
while (k >>= 1) dat[k] = F(dat[k*2], dat[k*2+1]);
}
/* get [a, b), a and b are 0-indexed */
Monoid get(int a, int b) {
Monoid vleft = UNITY, vright = UNITY;
for (int left = a + SIZE_R, right = b + SIZE_R; left < right; left >>= 1, right >>= 1) {
if (left & 1) vleft = F(vleft, dat[left++]);
if (right & 1) vright = F(dat[--right], vright);
}
return F(vleft, vright);
}
inline Monoid operator [] (int a) { return dat[a + SIZE_R]; }
/* debug */
void print() {
for (int i = 0; i < SIZE_R; ++i) {
cout << (*this)[i];
if (i != SIZE_R-1) cout << ",";
}
cout << endl;
}
};
int main() {
int N; cin >> N;
vector<long long> h(N), a(N);
for (int i = 0; i < N; ++i) cin >> h[i];
for (int i = 0; i < N; ++i) cin >> a[i];
// セグメント木 (区間取得を max としたもの)
SegTree<long long> dp(N+1,
[](long long a, long long b) { return max(a, b); },
0);
// 更新
long long res = 0;
for (int i = 0; i < N; ++i) {
// 値取得
long long A = dp.get(0, h[i]);
// 更新
if (dp.get(h[i], h[i]+1) < A + a[i]) {
dp.update(h[i], A + a[i]);
res = max(res, A + a[i]);
}
}
cout << res << endl;
}
6. インライン DP、とくに EDPC W - Intervals
LIS や EDPC Q - Flowers の解法は、
- 配列 ${\rm dp}[i]$ から配列 ${\rm dp}[i+1]$ への更新が一箇所のみで起こる
という構造を利用して in-place 化する手法でした。その更新部分においては、セグメント木を用いて高速化することが多いです。このように、DP を in-place 化した上でセグメント木に載せて高速化する手法は、とっても広く見られます!sky さんによってインライン DP と名付けられました。ここでは、インライン DP の例として、Educational DP Contest W - Intervals を解いてみましょう。かなり難しい問題です。
問題概要
長さ $N$ の $0$ と $1$ からなる文字列 $S$ を考えます。
この文字列のスコアを次のように計算します。
- 各 $i; (1 \le i \le M)$ について、$l_i$ 文字目から $r_i$ 文字目までに 1 がひとつ以上含まれるならば、スコアに $a_i$ を加算する。
文字列のスコアとして考えられる最大値を求めてください。
制約
- $1 \le N, M \le 2 \times 10^5$
考え方
区間についてどうのこうのする問題は、多くの場合、インライン DP になります。まずは区間を終端でソートして考えることにします。そして区間を順に処理していくような DP は、以下のようにするのが常套手段です。
【区間の問題で、あるあるな DP】
${\rm dp}[i][ (\text{何か}) ] := N$ マスのうちの最初から $i$ マス分について考える。$M$ 個の区間のうち、その範囲内に収まっているものについてはどのように扱うかを決めたときの、(何か) な状態となっている場合についての、スコアの最大値
そして各 $i = 1, 2, \dots, N$ について、右端が $i$ であるような区間を順に処理していくイメージです。今回の問題の場合、次のような DP が自然に立つでしょう。
- ${\rm dp}[i][j] :=$ 文字列の左から $i$ 文字分について 0-1 を決める方法のうち、最後に 1 にした index が $j$ (ここでは 1-indexed にします) である場合についての、区間の終端が $[0, i)$ の範囲内に収まっているようなものについての、スコアの総和の最大値
そして、$i-1$ から $i$ への更新を考えます。
S[i - 1] を 1 にするとき
S[i - 2] までは 0 か 1 かを決めていて、S[i - 1] について決定しようとしている場面です。S[i - 1] を 1 にする場合は比較的明快です。
右端が $i$ であるような各区間 $[l, i)$ のスコアの総和を $A$ とすると、
- ${\rm dp}[i][i] = \max_{0 \le j < i} {\rm dp}[i-1][j] + A$
となります。
S[i - 1] を 0 にするとき
$i$ を右端にもつような各区間 $[l, i)$ (スコア $v$) に対して、
- $j \le l$ ならば、${\rm dp}[i][j] = {\rm dp}[i-1]$[j]$ となります。これは in-place 化で消える部分です。
- $j > l$ ならば、${\rm dp}[i][j] = {\rm dp}[i-1][j] + v$ となります。これは dp 配列の区間 $[l+1, i)$ に一様に値 $v$ を加算することを意味しています。
in-place 化してまとめると
以上の DP を in-place 化して処理内容をまとめると、$i-1$ から $i$ への更新部分は、以下のように表すことができます。なお、右端が $i$ であるような区間のスコアの総和を $A$ とします。
- 配列 ${\rm dp}$ の区間 $[0, i)$ の最大値を $m$ として、${\rm dp}[i]$ の値を $m + A$ に更新します。
- 各区間 $[l, i)$ (スコア $v$) に対して、配列 ${\rm dp}$ の区間 $[l+1, i)$ に一様に値 $v$ を加算します。
これを実現するためには、以下のことができるセグメント木が欲しいです。そのようなものは俗称で Starry Sky 木とよばれています。
- 数列の区間 $[l, r)$ の最大値を取得 ( $O(\log{N})$ )
- 数列の区間 $[l, r)$ に値 $v$ を一様に加算 ( $O(\log{N})$ )
Starry Sky 木についての解説は、ここでは他の方にお任せすることにして、EDPC W 問題を解くコードを示します。計算量は $O( (N+M)\log{N})$ となります。
# include <iostream>
# include <vector>
# include <algorithm>
# include <functional>
using namespace std;
const long long INF = 1LL<<60;
// 抽象化した遅延評価付きセグメント木
template<class Monoid, class Action> struct SegTree {
using FuncMonoid = function< Monoid(Monoid, Monoid) >;
using FuncAction = function< void(Monoid&, Action) >;
using FuncLazy = function< void(Action&, Action) >;
FuncMonoid FM;
FuncAction FA;
FuncLazy FL;
Monoid UNITY_MONOID;
Action UNITY_LAZY;
int SIZE, HEIGHT;
vector<Monoid> dat;
vector<Action> lazy;
SegTree() { }
SegTree(int n, const FuncMonoid fm, const FuncAction fa, const FuncLazy fl,
const Monoid &unity_monoid, const Action &unity_lazy)
: FM(fm), FA(fa), FL(fl), UNITY_MONOID(unity_monoid), UNITY_LAZY(unity_lazy) {
SIZE = 1; HEIGHT = 0;
while (SIZE < n) SIZE <<= 1, ++HEIGHT;
dat.assign(SIZE * 2, UNITY_MONOID);
lazy.assign(SIZE * 2, UNITY_LAZY);
}
void init(int n, const FuncMonoid fm, const FuncAction fa, const FuncLazy fl,
const Monoid &unity_monoid, const Action &unity_lazy) {
FM = fm; FA = fa; FL = fl;
UNITY_MONOID = unity_monoid; UNITY_LAZY = unity_lazy;
SIZE = 1; HEIGHT = 0;
while (SIZE < n) SIZE <<= 1, ++HEIGHT;
dat.assign(SIZE * 2, UNITY_MONOID);
lazy.assign(SIZE * 2, UNITY_LAZY);
}
/* set, a is 0-indexed */
void set(int a, const Monoid &v) { dat[a + SIZE] = v; }
void build() {
for (int k = SIZE - 1; k > 0; --k)
dat[k] = FM(dat[k*2], dat[k*2+1]);
}
/* update [a, b) */
inline void evaluate(int k) {
if (lazy[k] == UNITY_LAZY) return;
if (k < SIZE) FL(lazy[k*2], lazy[k]), FL(lazy[k*2+1], lazy[k]);
FA(dat[k], lazy[k]);
lazy[k] = UNITY_LAZY;
}
inline void update(int a, int b, const Action &v, int k, int l, int r) {
evaluate(k);
if (a <= l && r <= b) FL(lazy[k], v), evaluate(k);
else if (a < r && l < b) {
update(a, b, v, k*2, l, (l+r)>>1), update(a, b, v, k*2+1, (l+r)>>1, r);
dat[k] = FM(dat[k*2], dat[k*2+1]);
}
}
inline void update(int a, int b, const Action &v) { update(a, b, v, 1, 0, SIZE); }
/* get [a, b) */
inline Monoid get(int a, int b, int k, int l, int r) {
evaluate(k);
if (a <= l && r <= b)
return dat[k];
else if (a < r && l < b)
return FM(get(a, b, k*2, l, (l+r)>>1), get(a, b, k*2+1, (l+r)>>1, r));
else
return UNITY_MONOID;
}
inline Monoid get(int a, int b) { return get(a, b, 1, 0, SIZE); }
inline Monoid operator [] (int a) { return get(a, a+1); }
/* debug */
void print() {
for (int i = 0; i < SIZE; ++i) { cout << (*this)[i]; if (i != SIZE) cout << ","; }
cout << endl;
}
};
using pll = pair<int, long long>;
int main() {
int N, M;
cin >> N >> M;
// 右端が i であるような区間の左端
vector<vector<pll>> lefts(N+1);
for (int i = 0; i < M; ++i) {
int l, r;
long long a;
cin >> l >> r >> a;
--l, --r; // 0-indexed に
++r; // 右側を開区間に
lefts[r].push_back({l, a});
}
// DP in Starry Sky Tree
auto fm = [](long long a, long long b) { return max(a, b); };
auto fa = [](long long &a, long long d) { a += d; };
auto fl = [](long long &d, long long e) { d += e; };
SegTree<long long, long long> dp(N+2, fm, fa, fl, -INF, 0);
dp.update(0, 1, -dp.get(0, 1)); // dp[0] = 0 の状態にします
for (int i = 1; i <= N; ++i) {
long long A = 0;
for (auto p : lefts[i]) A += p.second;
long long ma = dp.get(0, i);
// ma + A - dp.get(i, i+1) を加算すれば ma + A になる
dp.update(i, i+1, ma + A - dp.get(i, i+1));
for (auto p : lefts[i]) {
int l = p.first;
long long a = p.second;
dp.update(l+1, i, a);
}
}
// 答えは dp[0], ..., dp[N] の最大値
cout << dp.get(0, N+1) << endl;
}
7. おわりに
配列使いまわしによって DP の次元を減らすテクニックは、意外と解説が見当たらないのでまとめてみました。ナップサック DP のメモリ使用量を節約したり、ある種の問題に対しては、計算量削減にもつながることを示しました。
ところで、全頂点対間最短路を求める Warshall--Floyd 法も、三次元な DP を in-place にして二次元にしたものになっています。意外と in-place な DP は身近な存在です。
是非、このような DP を「実家のような安心感がある」といえるように... (なりたいですね!)
-
たとえば Educational DP Contest A - Frog 1 など。 ↩
-
たとえば Educational DP Contest E - Knapsack 1 など。 ↩
-
他にも「${\rm dp}[i] :=$ 最初の $i$ 項のみを考えた場合の、最後の要素が $a_{i-1}$ である場合についての、最長の長さ」とする方法もあります。この場合も自然に $O(N^2)$ な DP となります。 ↩
-
他にも演算の種類を変えて様々なことができます。 ↩