はじめに
ニューラルネットを使ったセミパラメトリックな密度推定の手法を考案しました。
Chainerによる実装(github)
確率密度関数 $f(x)=P(X=x)$ を直接ニューラルネットで学習しようとしても、
$$ \int_{-\infty}^{\infty}f(x)dx=1 $$
を満たすような制約を与えることは困難です。
しかし、累積分布関数 $F(x) = P(X \leq x)$ について考えると満たすべき制約は、
\frac{\partial}{\partial x}F(x) \geq 0 \\
F(-\infty)=0 \\
F(\infty)=1
であり、このうち単調増加性についてはその制約を満たすニューラルネットモデルが存在します。
Monotonic Networks, J.Sill (NIPS 1997)
今回はこのモデルをベースに、$F(x)$ を直接ニューラルネットに学習させてみました。
一次元の確率変数の場合
確率変数$ X $の観測データ$ \lbrace x_1, ...,x_N \rbrace $に対して、
$$ \underset{\theta}{\arg \min} \lbrace -\frac{1}{N}\sum_{i=1}^{N} \log f_\theta(x_i) \rbrace $$
を得たいので
$$-\frac{1}{N}\sum_{i=1}^{N}\log f_{\theta}(x_i)$$
を損失関数として$\theta$の学習を行います。
ここで、
$$f_{\theta}(x) = \frac{\partial}{\partial x}F_{\theta}(x)$$
ですが、これはChainerのDouble backpropagation機能で求めることができます(chainer.grad())。
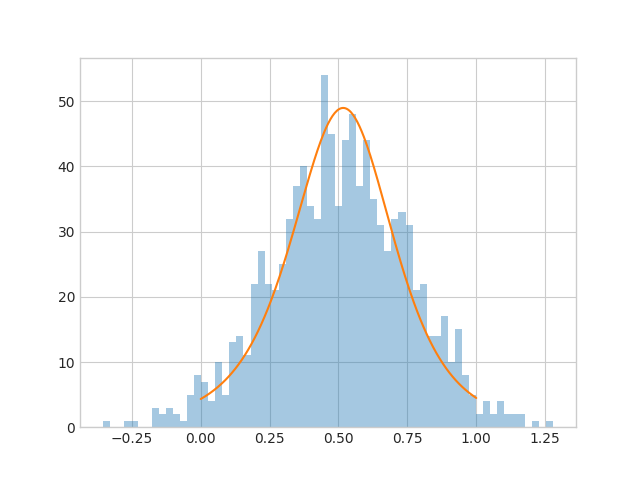
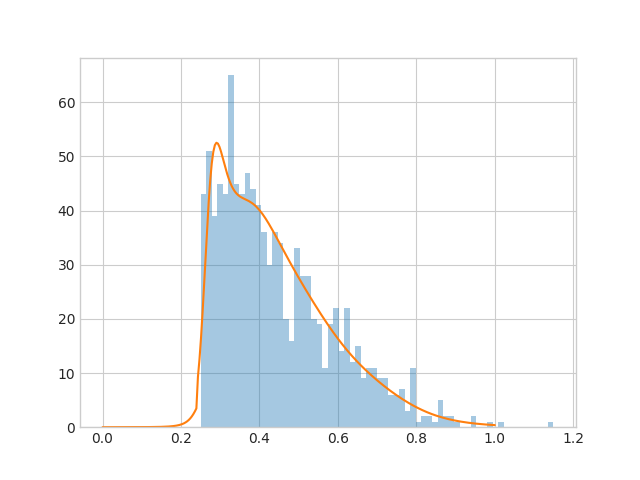
学習結果
オレンジ色の実線がモデルの出力した$P$です。
ガウス分布
切断ガウス分布
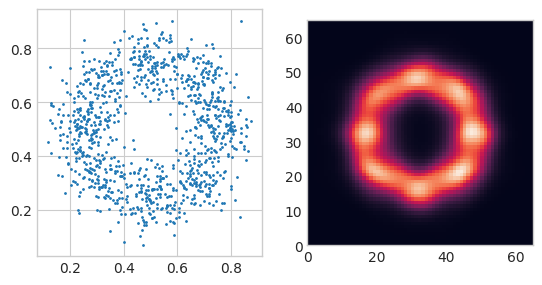
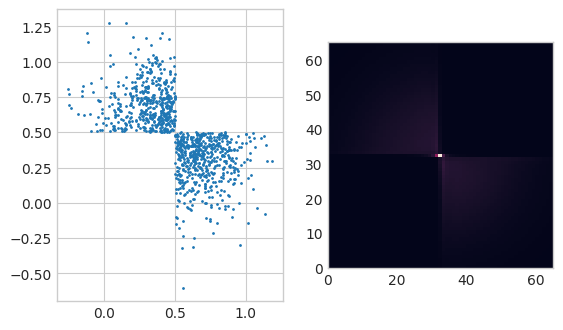
二次元の確率変数の場合
$$P(X, Y) = P(X) P(Y|X)$$
を計算すればよいです。
つまり$P(X)$と$P(Y|X)$をそれぞれ別のニューラルネットに学習させます。
右側がモデルの出力した確率密度です。
混合ガウス分布
切断(?)ガウス分布
最後の例はあまりうまく行っていないようです。
さらに次元が増えた場合も同様となるはずですが、まだ実験できていません。