はじめに
**最小二乗法はなぜ、差分の二乗和を考えるのか？**という疑問について答えるのが本稿の目的である。
ここでは、最小二乗法の一般的な説明
１．データと近似関数値の差分の二乗和を作る。
２．上の二乗和をパラメータごとに偏微分して、その共通零点を求める。
には殆どふれずに、上の１．に至るまでの思想について自分なりに記述してみたい。もちろん、最小二乗法はとても広い応用を持つが、本稿では直線近似に限定して、「最小二乗法のこころ」に迫りたい。
３点を直線近似する
平面にいくつかの点を与えたときに、その点を通る直線はどれだけあるか？ということから考え始めてみる。
1点を通る直線は無限個存在する。
異なる2点を通る直線は１つだけ存在する。
互いに異なる3点を通る直線は一般には存在しない。
（もちろん、最初から直線上にある3点を選んだとすれば直線が存在する。）
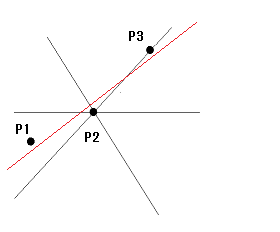
純粋な幾何学ならば「ここから先は考えない！」と言い切っても良いだろう。ただ、応用的な立場に立つならば「3点をちょうど通る直線は存在しなくても、例えば上図の赤い直線のようにできるだけ3点に近い直線を求めたい。」ということになる。そこで、直線近似の出番である。
素朴に考えてみる
上図の$P_1$と$P_2$に直線を近づけると$P_3$からは遠ざかる。
また、$P_2$と$P_3$に直線を近づけると$P_1$からは遠ざかり、
同様に$P_3$と$P_1$に直線を近づけると$P_2$からは遠ざかる。
どうも$P_1,P_2,P_3$を別々に考えていると、あちらを立てればこちらが立たずとなってしまい、考えが発散しそうになる。また「できるだけ3点に近い直線」とは何か？...等々思いめぐらしてみた。
最小二乗法のこころに迫る
そして、次のことが大事であると思うようになった。
平面上の3点 $P_1,P_2,P_3$を一組の対象（一つの点）として考えること
これは、直線をいい具合に$P_1,P_2,P_3$に近づけるために必要と考えた。そして、これができれば**「できるだけ3点に近い直線」を定義**できるのではないか？
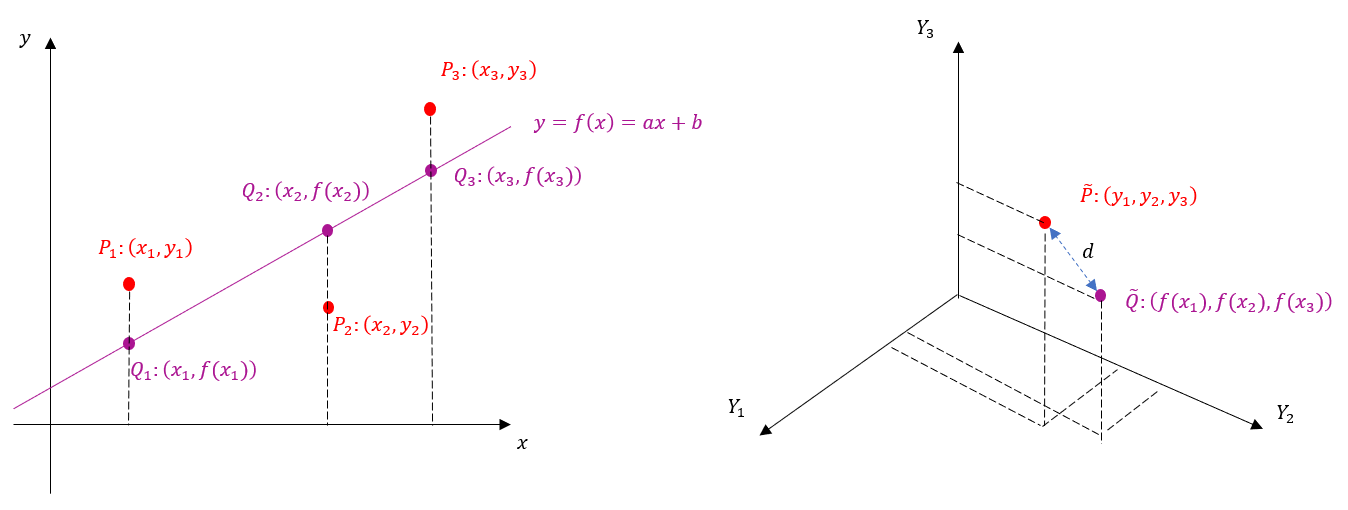
そこで、座標系を導入して実際に平面上の３点を１点としてみたい。下の左図ように通常の座標系 $(x,y)$ を導入して、$P_1$、$P_2$、$P_3$の座標がそれぞれ $(x_1,y_1)$、$(x_2,y_2)$、$(x_3,y_3)$であるとする。また、今は直線近似したいので、直線の式を $y=f(x)=ax+b$ と表しておく。さらに、$x=x_1$ における直線上の点を $Q_1$、$x=x_2$ における直線上の点を $Q_2$、$x=x_3$ における直線上の点を $Q_3$ とすれば、座標はそれぞれ$(x_1,f(x_1))$、$(x_2,f(x_2))$、$(x_3,f(x_3))$ となる。
$Q_1$、$Q_2$、$Q_3$ が $P_1$、$P_2$、$P_3$ に近づけば、直線が $P_1$、$P_2$、$P_3$ に近づく。 $Q_i (i=1,2,3)$ と $P_i (i=1,2,3)$ を比較すると、$x$ 座標は共通なので、$f(x_i)(i=1,2,3)$ を $y_i(i=1,2,3)$ に近づければよい。そこで、上の右図のように新たに3次元空間（ここではデータベクトル化空間と呼んでおく）に座標系 $(Y_1,Y_2,Y_3)$ を導入する。そして、 $(y_1,y_2,y_3)$ なるベクトルを考えて$\tilde P$ とする。これで平面上の3点を1点にできた。同様に $(f(x_1),f(x_2),f(x_3))$ なるベクトルを考えて $\tilde Q$ とする。さらに、$\tilde P$ と $\tilde Q$ 2点間の距離を $d$ とする。いよいよ、**「最小二乗法のこころ」について述べたい。上で定義してきた記号を用いると、それは、「$\tilde P$ と $\tilde Q$ 2点間の距離 $d$ を最小にするような$a,b$を求めること。」**となる。
そして、**そのような$a,b$に対応する直線 $y=ax+b$を「できるだけ3点に近い直線」**と定義する。
ところで、$d$ は三平方の定理を応用すれば下の式で求められる。
d = \sqrt{(f(x_1)-y_1)^2 + (f(x_2)-y_2)^2 + (f(x_3)-y_3)^2}
そして、$d$を最小にするのは、$d^2$を最小にするのと同じである。すなわち、
d^2 = (f(x_1)-y_1)^2 + (f(x_2)-y_2)^2 + (f(x_3)-y_3)^2 （差分の二乗和！）を最小にするべき。
かくして、冒頭の「１．データと近似関数値の差分の二乗和を作る。」までたどり着いたことになる。
3Dアニメーションで見てみる。
以上で述べた「最小二乗法のこころ」を可視化するために、Pythonで作成した3Dアニメーションを下に添付した。グラフで用いた記号などは上述してあるので、必要に応じて今までの説明を参照願いたい。
左上：$a,b$ に対する $d^2$ の値をプロットした3Dグラフ
右上：データベクトル化空間に、$a,b$ に対する $\tilde Q$ （紫）をプロットした3Dグラフ。赤点は $\tilde P$ を示す。
左下：$a,b$ に対する直線をプロットしたグラフ
ここでは、最初に与える3点の座標は $P_1:(-7, -8), P_2:(4, 3), P_3:(8, 9)$ としてある。
最小二乗法の解は $a=200/181,b=-92/181$ である。また、アニメーションの１コマごとに$a$の値を変化させている。$b$ については最小二乗法の解$b=-92/181$ に固定してある。
そして、最後の１コマは最小二乗法の解 $a=200/181,b=-92/181$ におけるグラフになっている。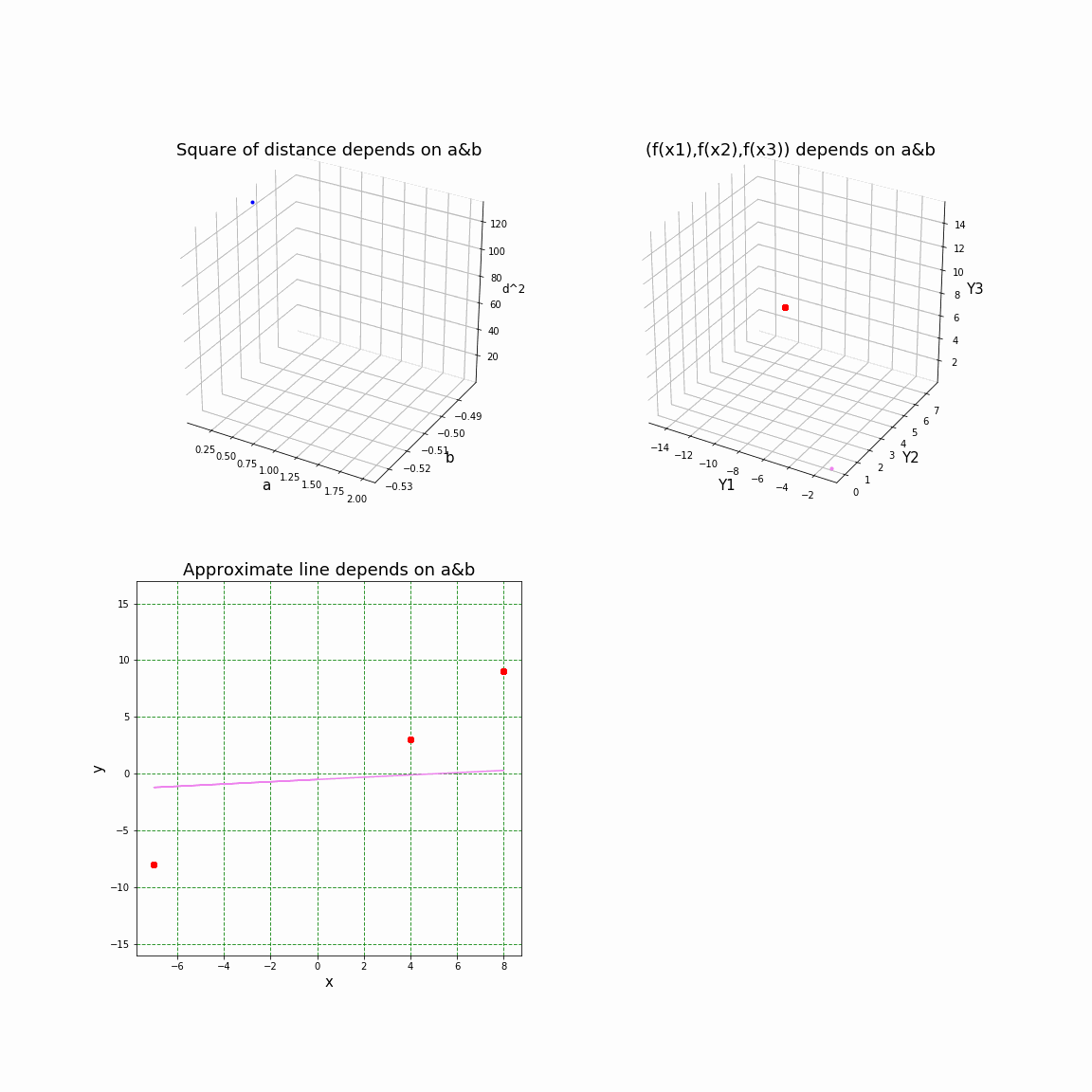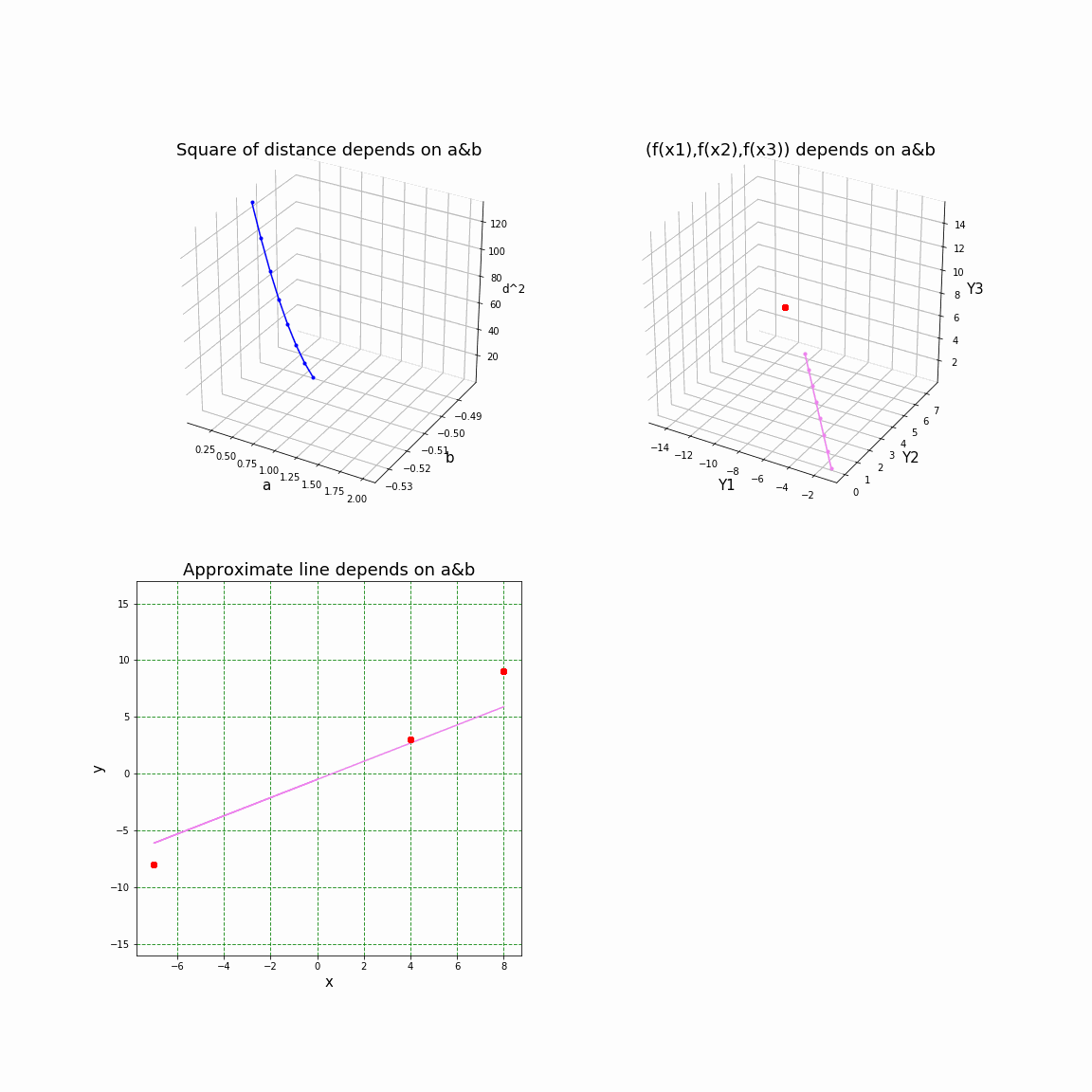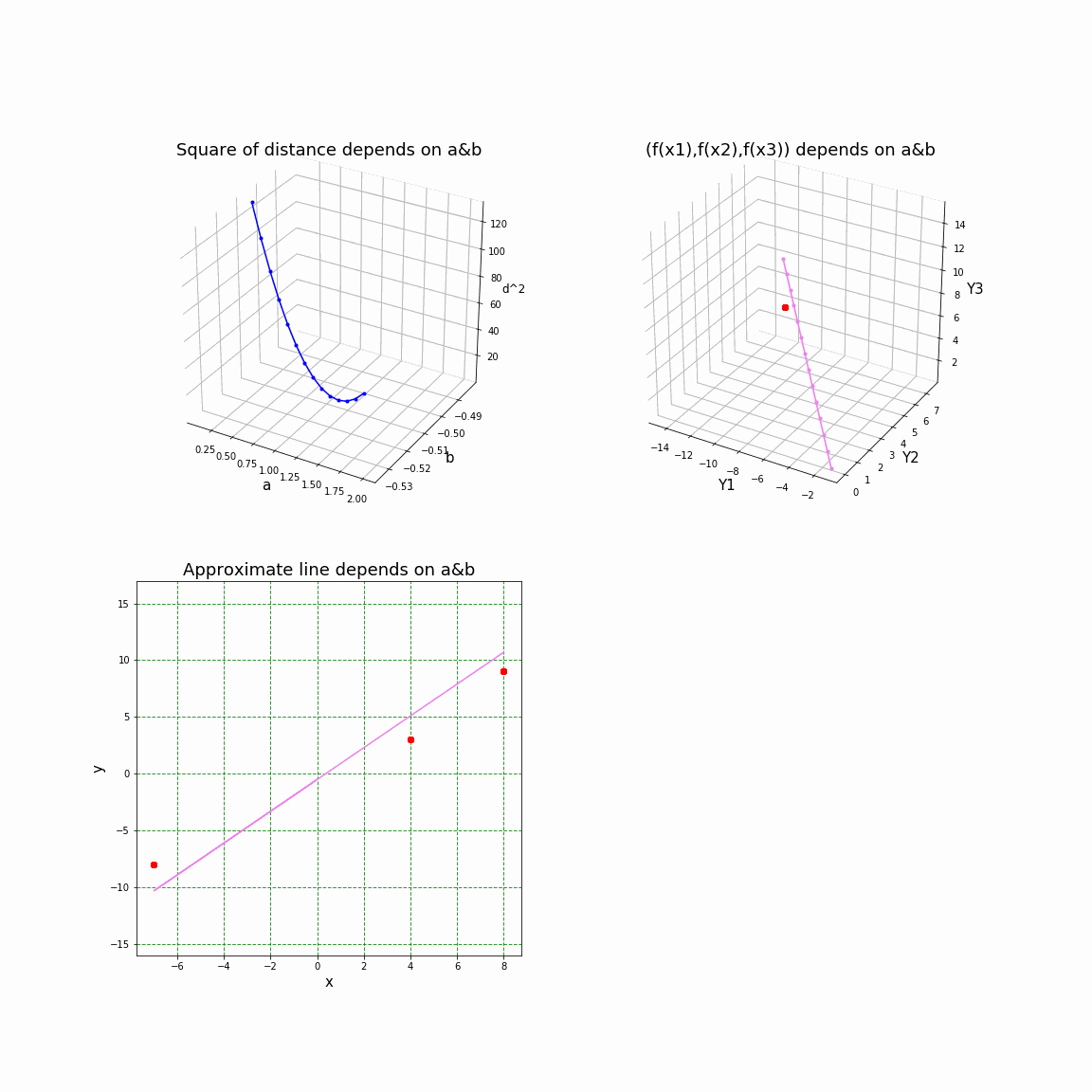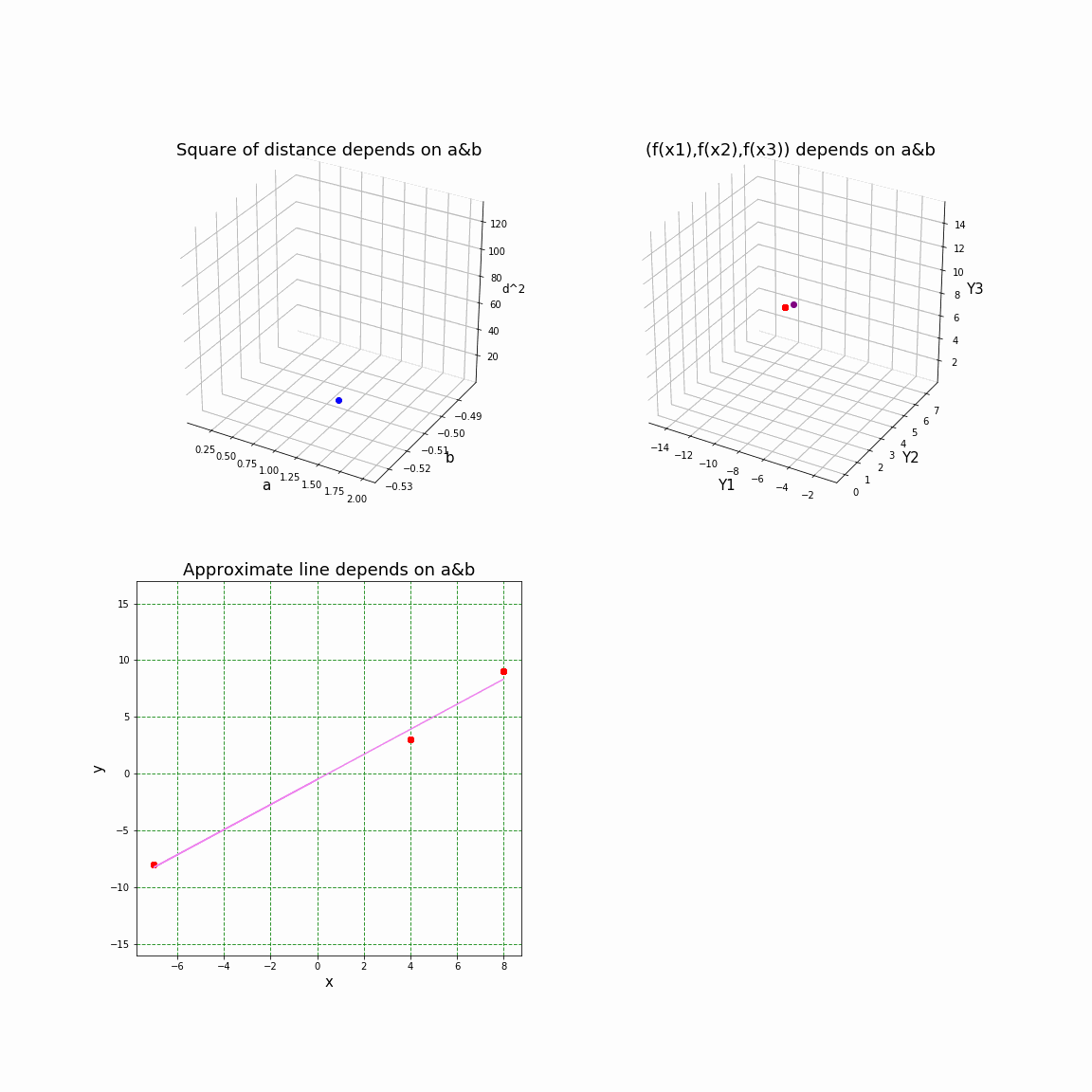
（上をクリックすると、アニメーションを再生）
Pythonプログラム
上記の3Dアニメーションを描くPythonプログラムのコードは以下のとおり。
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from mpl_toolkits.mplot3d import Axes3D
f = lambda a,b,x : a*x+b #直線の式
sqfy = lambda a,b,x,y:(f(a,b,x)-y)**2 #近似直線とデータの差分の2乗
d2fy = lambda a,b,x,y:sqfy(a,b,x,y).sum() #近似直線とデータの差分の2乗和
srcdata = [[-7, -8], [4, 3], [8, 9]] #データ点
ars = np.array(srcdata)
src_x = np.array([ars[0][0],ars[1][0],ars[2][0]]) #データ点のx座標
src_y = np.array([ars[0][1],ars[1][1],ars[2][1]]) #データ点のy座標
#グラフ準備
fig = plt.figure(figsize=4*plt.figaspect(1.0))
plt.subplots_adjust(hspace=0.2)
ax1 = fig.add_subplot(2, 2, 1, projection='3d') #a,b に対する d2 の値をプロット(3Dグラフ)
ax2 = fig.add_subplot(2, 2, 2, projection='3d') #a,b に対する Q~ （紫）をプロット(3Dグラフ)。固定点としては P~ も描画する。
ax3 = fig.add_subplot(2, 2, 3) #a,b に対する直線をプロットしたグラフ
imgs = [] #アニメーションのコマの配列
#a,bの値を設定
#最小二乗法の解は、a=200/181,b=-92/181
#最後のデータは、最小二乗法の解に対応するデータとする
#今回は理解しやすいようにbの値は１つに固定しておく
ao=np.arange(0.1,2.1,0.1)
a=np.insert(ao,20,[200/181])
bv=-92/181
b=bv*np.ones(21)
#アニメーションのコマで使うデータ配列
ys0=[]
ys1=[]
ys2=[]
d2=[]
fy0=[]
fy1=[]
fy2=[]
for ma in a:
ys0.append(src_y[0])
ys1.append(src_y[1])
ys2.append(src_y[2])
d2.append(d2fy(ma,bv,src_x,src_y))
fy=f(ma,bv,src_x)
fy0.append(fy[0])
fy1.append(fy[1])
fy2.append(fy[2])
# 各グラフのタイトルや軸ラベル
ax1.set_title("Square of distance depends on a&b",fontsize=18)
ax1.set_xlabel("a",fontsize=15)
ax1.set_ylabel("b",fontsize=15)
ax1.set_zlabel("d^2",fontsize=12)
ax2.set_title("(f(x1),f(x2),f(x3)) depends on a&b",fontsize=18)
ax2.set_xlabel("Y1",fontsize=15)
ax2.set_ylabel("Y2",fontsize=15)
ax2.set_zlabel("Y3",fontsize=15)
ax3.set_title("Approximate line depends on a&b",fontsize=18)
ax3.set_xlabel("x",fontsize=15)
ax3.set_ylabel("y",fontsize=15)
ax3.grid(which = "major", axis = "x", color = "green", alpha = 0.8,linestyle = "--", linewidth = 1)
ax3.grid(which = "major", axis = "y", color = "green", alpha = 0.8,linestyle = "--", linewidth = 1)
for i in range(len(a)):
if (i < len(a)-1 ):
#軌跡を描画
img1 = ax1.plot(a[:i+1], b[:i+1], d2[:i+1],marker=".",color="blue")
img2 = ax2.plot(ys0[:i+1],ys1[:i+1],ys2[:i+1],marker="o",color="red")
img2 = ax2.plot(fy0[:i+1], fy1[:i+1],fy2[:i+1], marker=".",color="violet")
else:
#最後の１コマは最小二乗法の解について描画
img1 = ax1.plot([a[i]], [b[i]], [d2[i]],marker="o",color="blue")
img2 = ax2.plot([ys0[i]],[ys1[i]],[ys2[i]],marker="o",color="red")
img2 = ax2.plot([fy0[i]], [fy1[i]],[fy2[i]], marker="o",color="purple")
#a,bの値に対応する直線を描画する
lptX=[]
lptY=[]
lptX.append(0)
lptX.append(src_x[0])
lptX.append(src_x[2])
lptY.append(bv)
lptY.append(fy0[i])
lptY.append(fy2[i])
img3 = ax3.plot(src_x[0],src_y[0],marker="o",color="red")
img3 = ax3.plot(src_x[1],src_y[1],marker="o",color="red")
img3 = ax3.plot(src_x[2],src_y[2],marker="o",color="red")
img3 = ax3.plot(lptX,lptY,color="violet")
imgs.append(img1+img2+img3) #コマの情報を追加
anim = animation.ArtistAnimation(fig, imgs, interval=500) #アニメーションの作成
anim.save('resulta.gif', 'imagemagick') #gifファイルに保存
plt.show()
（付録）データベクトル化空間における幾何学と相関係数
上のアニメーションでは $b$ を固定していたが、$a,b$ ともに独立に変化させると、$ \tilde Q(a,b):=(-7a+b,4a+b,8a+b)$ 全体が作る軌跡は平面（$H$ と表記）になる。$d$ が最小値 $d_{min}$になるとき、$ \tilde Q$ は $ \tilde P$ から平面$H$ におろした垂線の足になる。これは数式によって確かめることができる。$O$ をデータベクトル化空間の原点、$<,>$ を標準的な内積として、実際に最小二乗法を実行してみると、
\begin{eqnarray}
\vec{q}(a,b)&:=& \vec{O\tilde Q}\\\vec{p} &:=& \vec{O\tilde P}\\
d^2&=&<\vec{q}(a,b)-\vec{p},\vec{q}(a,b)-\vec{p}>\\
&=& <\vec{q}(a,b),\vec{q}(a,b)>-2<\vec{q}(a,b),\vec{p}>+<\vec{p},\vec{p}>\\
\frac{\partial (d^2)}{\partial a} &=& 2<\frac{\partial \vec{q}(a,b)}{\partial a},\vec{q}(a,b)> - 2<\frac{\partial \vec{q}(a,b)}{\partial a},\vec{p}>\\
&=& 2<\frac{\partial \vec{q}(a,b)}{\partial a},\vec{q}(a,b)-\vec{p}>\\
\frac{\partial (d^2)}{\partial b} &=& 2<\frac{\partial \vec{q}(a,b)}{\partial b},\vec{q}(a,b)-\vec{p}>\\
\frac{\partial (d^2)}{\partial a} &=& \frac{\partial (d^2)}{\partial b} = 0\\
&\Leftrightarrow& <\frac{\partial \vec{q}(a,b)}{\partial a},\vec{q}(a,b)-\vec{p}> = 0 ,<\frac{\partial \vec{q}(a,b)}{\partial b},\vec{q}(a,b)-\vec{p}> = 0\\
\therefore \space\space \frac{\partial \vec{q}(a,b)}{\partial a} &\perp& (\vec{q}(a,b)-\vec{p}),\frac{\partial \vec{q}(a,b)}{\partial b} \perp (\vec{q}(a,b)-\vec{p})
\end{eqnarray}
が一般に成り立つ。もし、$\phi:(a,b) \rightarrow \tilde {Q}(a,b)$ が埋め込み写像ならば、$\frac{\partial \vec{q}(a,b)}{\partial a}$ 、$\frac{\partial \vec{q}(a,b)}{\partial b}$ は多様体の$\tilde {Q}(a,b)$ における接平面を張るので、$\vec{q}(a,b)-\vec{p}$ は接平面に直交する。今の場合、$\phi$ は3次元空間の中への埋め込みで、平面 $H$ に写るので、$\vec{q}(a,b)-\vec{p}$ は平面 $H$ に直交する。下図参照。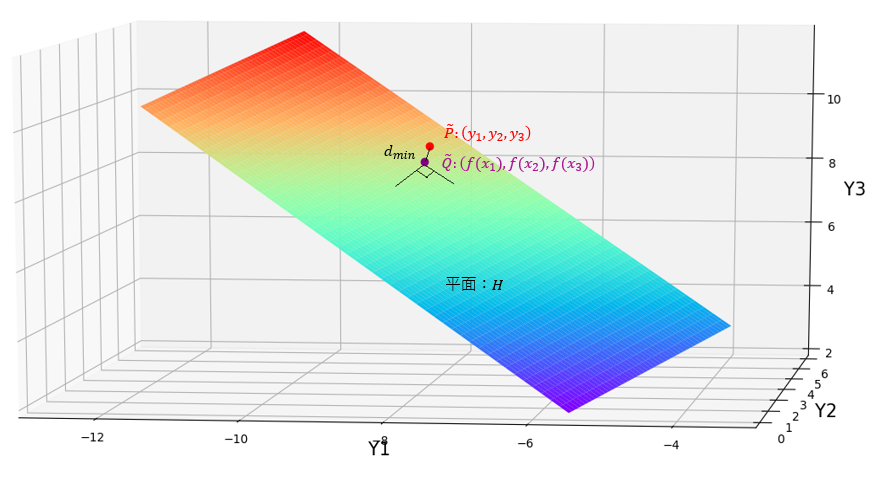
また、$d$ が最小値 $d_{min}$になるとき、$\bar x$ を$x_i (i=1,2,3)$ の平均値、$\bar y$ を$y_i (i=1,2,3)$ の平均値とおくと、$a,b$ は下のように表せる。
\begin{eqnarray}
a &=& \frac{\sum_{i=1}^{3}(x_i - \bar x)(y_i - \bar y)}{\sum_{i=1}^{3}(x_i - \bar x)^2}\\
b &=& \bar y - a\bar x
\end{eqnarray}
上の式を用いて、さらに${d_{min}}^2$ を計算すると、下のようになり、相関係数と関係があることが分かる。
\begin{eqnarray}
{d_{min}}^2 &=& (\sum_{i=1}^{3}(y_i - \bar y)^2)(1-r^2)\\
ただし、r &=& \frac{\sum_{i=1}^{3}(x_i - \bar x)(y_i - \bar y)}{\sqrt{(\sum_{i=1}^{3}(x_i - \bar x)^2)(\sum_{i=1}^{3}(y_i - \bar y)^2)}} （{x_i}と{y_i}の相関係数）
\end{eqnarray}
このように、最小二乗法のこころには高次元の幾何学が隠れていて、統計量などとも関連を持つ事が分かった。
ここでは、3点を与えたのでデータベクトル化空間は3次元だったが、一般に$N$ 個の点を与えらえた場合にはデータベクトル化空間は$N$次元になる。そして、直線近似を他の関数による近似に置き換えることで、より豊かな高次元の幾何学が現れるのではないか？と期待して、本稿を終わりにする。
参考
１では、アニメーションで軌跡を描く方法を参考にさせていただいた。
２では、複数のグラフを一つのアニメーションに含める方法を参考にさせていただいた。
１．matplotlib で線分をアニメーションさせる
２．[matplotlib アニメーション (Jupyter)]
(https://qiita.com/pegasusBS15/items/3445c5ad1a70f61c85d4)