関数はどこで零になるか?できれば全部知りたい!
与えられた区間内で連続な一変数実数関数を対象にして、その零点を(なるべく)もれなく求めることを目的とする。ただし、区間内の零点の数は有限個と仮定する。また、微分可能性は仮定していないので、零点の探査に微分を使えないことを強調しておく。
ここでは次の例を使って説明してみる。
f(x)=(x-2)x(x+2)^2\\
x \in [-2.5,2.5]
人間が見れば、次のようにすべての零点を求めることができる。$$ x=-2(重根) , 0 , 2 $$
ところが、コンピュータプログラムで同様の事をするのは案外難しいようである。
実際にPythonでよく使われるライブラリScipyの零点を求める関数を使ってみる。
まず、Pythonで上の関数を定義する。
f=lambda x:(x-2.0)*x*(x+2.0)**2
Scipyの関数を使った例
Brent法の関数 scipy.optimize.brentq(f,a,b)で零点が1つ求まる。
ただし、$f(a)$ と $f(b)$ は異符号であることが必要。
from scipy import optimize
broot=optimize.brentq(f,-2.5,1.5)
print(broot)
"""
1.9808730768636993e-15
"""
Newton法の関数 optimize.newtonによって、初期値の近くにある零点が1つ求まる。
nroot1=optimize.newton(f,-2.5)
print(nroot1)
"""
-2.000000017616174
"""
nroot2=optimize.newton(f,-0.5)
print(nroot2)
"""
3.972677122927984e-14
"""
nroot3=optimize.newton(f,1.5)
print(nroot3)
"""
2.0
"""
このように、真の零点の位置に関するヒントを付加した上で、1回の関数コールによって1つの零点が求まる。すなわち、網羅的に零点を求めるには、ヒントを適切に変えながら複数回コールする必要がある。
このような感じで、もれなく零点を求める関数が見当たらなかったので、この道の専門家でもないのに、なぜか自前で作ってみようと思った。今回、一定の結果が得られたので、ここに紹介する。
自作関数の使用例
零点を求める
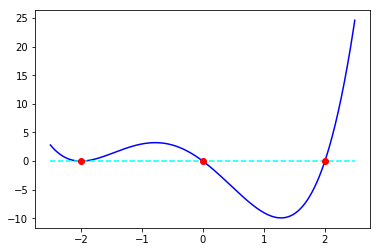
上の関数 $f(x)=(x-2)x(x+2)^2$ に対して、DepthMethodの関数SearchZeroPtByDepthを適用した結果は下記の通り、3つの零点を求められる。
from DepthMethod import SearchZeroPtByDepth
Zeros,rdGoodNum=SearchZeroPtByDepth(f,'testfunction',-2.5,2.5)
Zero=Zeros[0]['EstimateZeroPt']
print(Zero)
"""
Good Number of Random Points : 430
0 -2.000000e+00
1 -3.081488e-33
2 2.000000e+00
Name: EstimateZeroPt, dtype: float64
"""
関数グラフに零点を重ねると下図のようになる。
import numpy as np
import matplotlib.pyplot as plt
x=np.arange(-2.5,2.5,0.01)
zr=np.zeros(500)
y=f(x)
plt.plot(x, y, marker="", color = "blue", linestyle = "-")
plt.plot(x, zr, marker="", color = "Cyan", linestyle = "--")
plt.plot(Zero, f(Zero), marker="o",color = "red" , linestyle = "" )
plt.show()
関数が連続微分可能(C1級)のときは臨界点を求められる(応用)
導関数の零点を網羅的に求めることで臨界点を得る。
from DepthMethod import numerical_diff
g=lambda x:numerical_diff(f,x,1e-10)
x=np.arange(-2.5,2.5,0.01)
y=f(x)
gy=g(x)
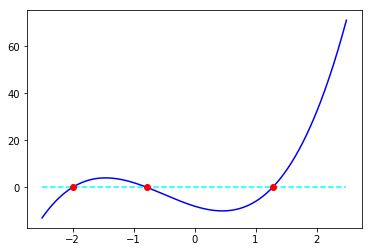
gZeros,rdGoodNum=SearchZeroPtByDepth(g,'gradient',-2.5,2.5)
gZero=gZeros[0]['EstimateZeroPt']
print(gZero)
"""
Good Number of Random Points : 200
0 -2.000000
1 -0.780777
2 1.280777
Name: EstimateZeroPt, dtype: float64
"""
plt.plot(x, gy, marker="", color = "blue", linestyle = "-")
plt.plot(x, zr, marker="", color = "Cyan", linestyle = "--")
plt.plot(gZero, g(gZero), marker="o",color = "red" , linestyle = "" )
plt.show()
plt.plot(x, y, marker="", color = "blue", linestyle = "-")
plt.plot(gZero, f(gZero), marker="o",color = "green" , linestyle = "" )
plt.show()\
導関数のグラフに零点を重ねると下図のようになる。
もとの関数グラフに(臨界点,臨界値)を重ねると下図のようになる。
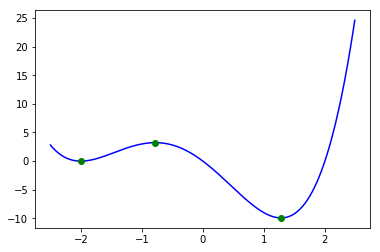
さらに、すべての臨界値と区間の端点での値を比較することで、最小値と最大値が求まることも分かる。
以下、しばらく私の独りよがりでかつ苦労話し的な内容なので、「Pythonコードの実行について」のテストプログラムを試してみてから戻ってくるのもよいかと思います。
そもそも関数値が零になるって...どう判定するの?
零点の定義による判定方法
もちろん、零点の定義は以下の通り。
x \in [a,b]が関数fの零点とは、f(x) = 0を満たすこと。
だからと言って、次のように関数値が0になる$x$を探査すればよいか?
if f(x) == 0:
#xはfの零点
この考えは、コンピュータプログラムを使う場合、次の2つの意味で非現実的であることが分かる。
・ちょうど真の零点を選らぶことが困難であること。実際、optimize.brentq、optimize.newton、SearchZeroPtByDepthでも真の零点から少しずれている。
・そもそも真の零点を表せない場合があること。例えば、下のPythonによるsin関数の計算結果を見れば、円周率$π$を正確には表せていないことが分かる($π$が無理数なので当たり前だが)。
np.sin(0)
"""0.0"""
np.sin(np.pi)
"""1.2246467991473532e-16""" #これは0にならないので、np.piは正確な円周率を表していない
関数値の絶対値を閾値で抑える判定方法
そこで、通常多くの場合は小さな閾値 $ε$ を使って下の関係が成立するときに零点と判断するであろう。
εが小さい正の数として、\\
-ε < f(x) < ε 、すなわち |f(x)| < ε
しかし、上の条件を満たす $x$ の集合
X = \{ x_1,x_2,....,x_n\}
が真の零点に十分近い点ばかりとは限らない。これは例えば、下図のように多項式 $f(x) = x^2$ の重根 $x=0$ の近傍を拡大すれば確認できる。
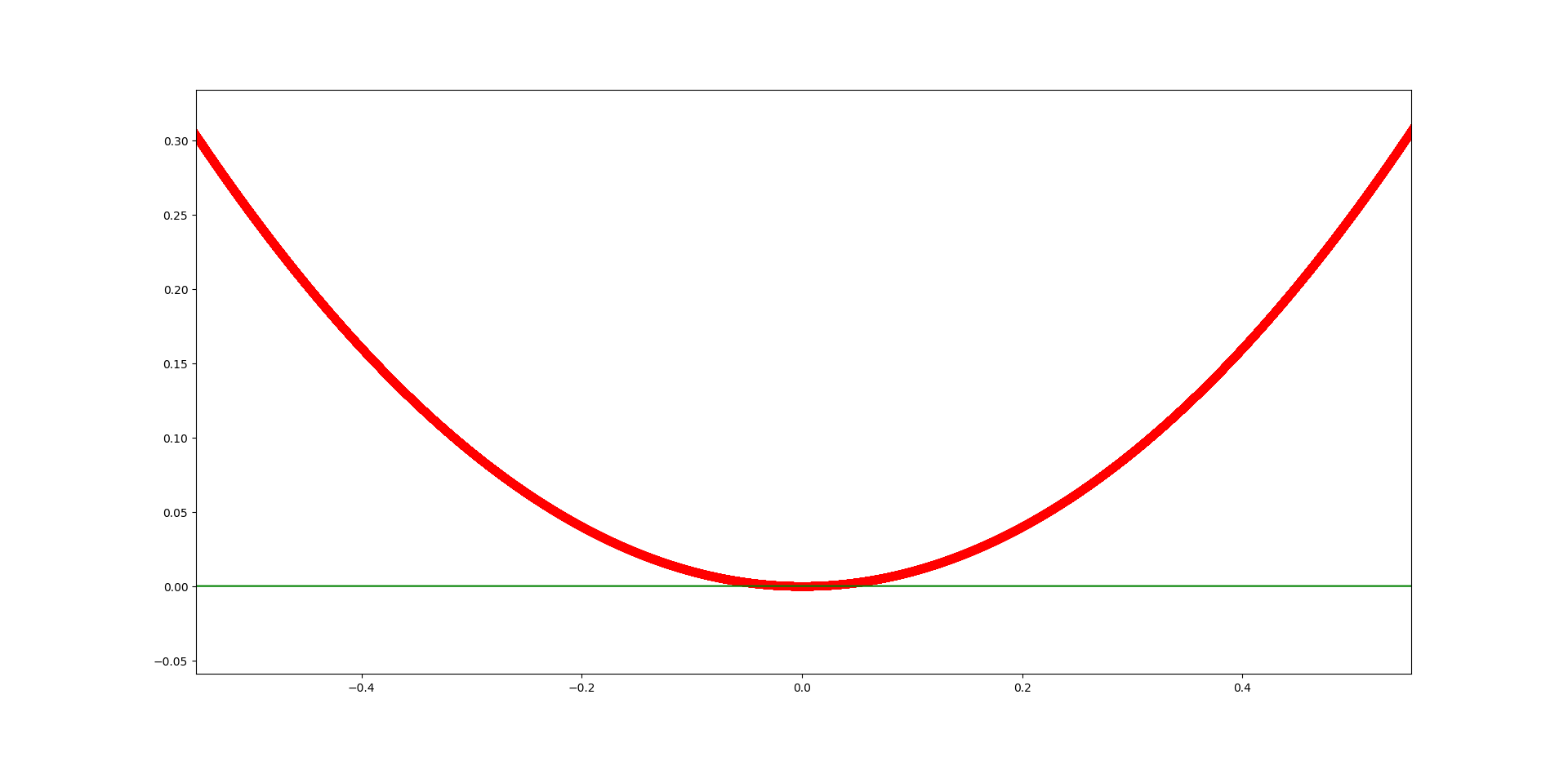
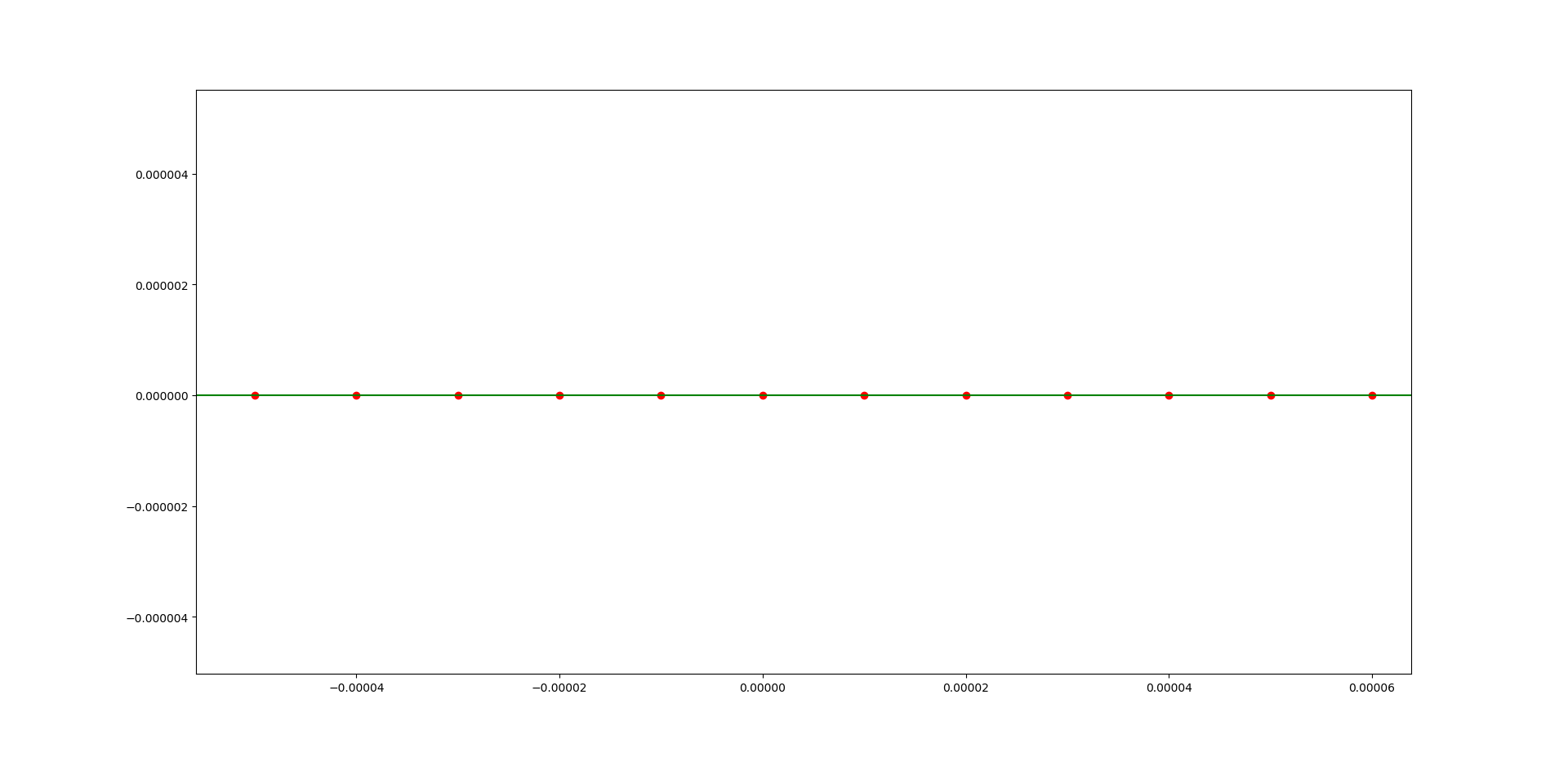
$ε \approx 1e-6$ の場合、上の図から少なくとも$ -1e-5 \leq x \leq 1e-5$の幅を持つ。
真の零点 $x=0$ に十分近い点を選ぶためには、 $ε\ll1e-6$ とする必要があるだろう。また、 $f(x) = x^3$ の3重根 $x=0$ に関してはさらに小さな $ε$ を設定する必要がある。すなわち、特定の $ε$ に固定すると、零点と判定できない場合が多々ある。
零点を求めることをあきらめる。
上に述べたことから、(目的から外れてしまうようだが)零点を求めることをあきらめてみる。と言っても、完全にあきらめるのではなく、零点になるかもしれない「零点の候補」を列挙するという発想に転換するのである。乱暴な話、零点でないものが含まれていても構わないから、なるべく「零点の候補」を漏らさないようにしたい。この辺りから、最初に仮定した関数の連続性が効いてくる。$x$ を真の零点 $x_z$ に近づけると関数値の絶対値 $|f(x)|$ が0に近くなる。そこで、$|f(x)|$ が小さくなっていくならば、「零点の候補」に近づいていると考えることにする。より端的な表現をするなら、極小点($|f(x)|$ が極小になる $x$) を「零点の候補」と考えることにする。
深さ法(Depth Method) (造語ですので一般的な表現ではない)
深さの定義(これも独創なので一般的ではない)
$|f(x)|$ の小ささを表す尺度を定義する。
基準値 $c>0$ を決めておいて、$c/2^n ( n=0,1,2,...)$ によって、横帯状の領域に分割する。
$(x,|f(x)|)$ がどの帯領域に含まれるかによって、$f(x)$ の深さを定義する。
xにおけるcを基準とする関数fの深さを
\\max\{ \lceil-log_2(|f(x)|/c)\rceil ,0\} (\lceil . \rceilは天井関数)で定義し、\\
depth_c,_x(f)と書くことにする。\\
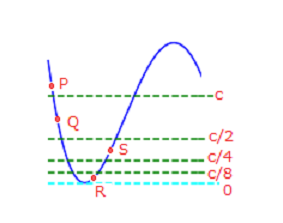
下の図のPからSのそれぞれの深さは、次のようになる。
Pの深さ = 0\\
Qの深さ = 1\\
Rの深さ = 4\\
Sの深さ = 2\\
$x$が零点に近いほど深さが大きいことが分かる。
また、定義から深さは0以上の整数である。
大局的探索(深さの利用)
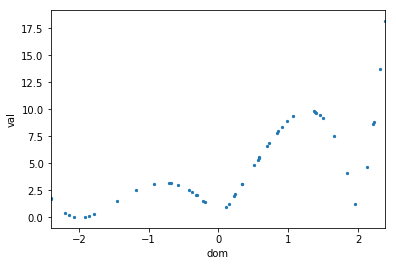
零点候補を探すために深さを利用したいが、そのためには $(x,f(x))$ をサンプリングする必要がある。ここでは区間内で乱数によって $x$ の値を決めた。なお、乱数には一様分布乱数(np.random.rand)を用いた。
上でも用いた関数
f(x)=(x-2)x(x+2)^2
に対して、実際に数十回ランダムに $|f(x)|$ をサンプリングした結果が次のグラフである。
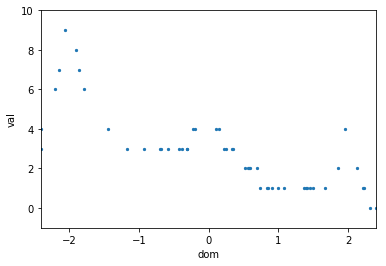
深さに変換した結果が次のグラフである。
深さのデータから棒グラフを作ると次のグラフになる。
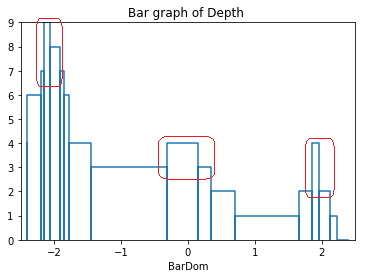
この結果は零点候補が3個であることを示している。
実は、一つの赤い四角で囲んだ3本の棒から次のような3組を得ることができる。このような3組は囲い込み法で登場する。
x_1 < x_2 < x_3\\
depth_c,x_1(f) < depth_c,x_2(f) > depth_c,x_3(f)\\
つまり、\\
x_1 < x_2 < x_3\\
|f(x_1)| > |f(x_2)| < |f(x_3)|
ここまでが大局的探索で、この後、局所的探索のステップとなる。
局所的探索
3つ組
x_1 < x_2 < x_3\\
|f(x_1)| > |f(x_2)| < |f(x_3)|
に対して連続関数$ |f(x)| $は、区間$ [x_1, x_3]$に少なくとも一つ極小値をとる。
さらに、例えば下記のようにして
#f(x1)>f(x2),f(x3)>f(x2) , x1 < x2 < x3
xo1 = x1
xo2 = x2
xo3 = x3
r0 = np.random.random_sample()
r=xo1+(xo3-xo1)*r0
#set points for bracketing
if ( r < x2):
if ( f(r) <= f(x2) ):
xo3 = x2
xo2 = r
else:
xo1=r
elif ( x2 < r ):
if ( f(x2) <= f(r) ):
xo3 = r
else:
xo1 = x2
xo2 = r
さらに狭い3組を求める。
x_1 \leq xo_1 < xo_2 < xo_3 \leq x_3(等号は一方のみ)\\
|f(xo_1)| > |f(xo_2)| < |f(xo_3)|
この場合も連続関数$ |f(x)| $は、区間$ [xo_1, xo_3]$に少なくとも一つ極小値をとる。
このように区間縮小を限界まで繰り返し、最後の $xo_2$ を極小点とする。
ここでの限界とは、理論上それ以上処理を続けても意味がない状況のこととする。例えば次の場合は数値計算誤差によってそれ以上処理を続けても意味がない。
乱数 r は1.0未満なので、理論的には r < xo_3なのに\\
数値計算誤差でr=xo_3になってしまう。
零点候補に対する注意
以上、大局的探索で零点がありそうな区間を見つけ、その1つ1つの区間において局所的探索によって極小点を求めることで、もれなく零点候補を列挙するプロセスを見てきた。ここで用いている方法に依存する注意点について記載する。
零点候補の中に零点でないものが含まれる。
各零点候補における関数値によって、コールした側で零点として扱うかどうか?を定める必要がある。
真の零点が零点候補からもれてしまう場合がある。
複数の零点が近いとき
局所的探索では区間の中に極小値が1つであるという想定で探索するため、複数の零点が極端に近い場合はもれてしまう可能性がある。
急な変化をして零になるとき
急な変化をして零になる関数として次のようなvalley関数を定義しておいた。グラフが$(0,0)$を底とする谷型をしているので、この名前を付けた。$a$ が小さいほど、急な谷になっている。
# valley function
def valley(a,x):
val=np.minimum(abs(x)/abs(a),1.0)
return val
$a=0.01$ の場合はデフォルト設定でも零点 $x=0$ を十分な精度で求めているが、$a=0.001$ の場合はデフォルト設定では零点候補を得ることができない。
from DepthMethod import SearchZeroPtByDepth
from DepthMethod import valley
f=lambda x:valley(0.01,x)
Zeros,rdGoodNum=SearchZeroPtByDepth(f,'testfunction',-2.5,2.5)
"""Good Number of Random Points : 210 """
print(Zeros)
"""
[ EstimateZeroPt FunctionValue Iteration
0 1.848893e-32 1.848893e-30 121]
"""
f=lambda x:valley(0.001,x)
Zeros,rdGoodNum=SearchZeroPtByDepth(f,'testfunction',-2.5,2.5)
"""Good Number of Random Points : 2000"""
print(Zeros)
"""
[Empty DataFrame
Columns: [EstimateZeroPt, FunctionValue, Iteration]
Index: []]
"""
このようなときにもパラメータを調整すると求められる可能性がある。
Zeros,rdGoodNum=SearchZeroPtByDepth(f,'testfunction',-2.5,2.5,InitRandNum=100)
"""Good Number of Random Points : 5800"""
print(Zeros)
"""
[ EstimateZeroPt FunctionValue Iteration
0 -1.232595e-32 1.232595e-29 105]
"""
大局的な探索の良いサンプリング数はどのくらい?
今まで、触れてこなかったが、SearchZeroPtByDepthを実行後に表示される
Good Number of Random Points : 430
の意味について説明する。
上述した大局的探索において大事なのは、対象とした関数の深さ情報を、乱数によってどの程度取得できているか?に尽きる。そこで情報理論でよく使われるKullback-Libler情報量の援用を思いついた。そのために、深さデータから作った棒グラフに比例する確率密度関数を $p(x)$ と表す。また与えられた区間 $[a,b]$ における一様分布確率密度関数を $q(x)$ とする。すなわち、
p(x) \propto 深さデータから作った棒グラフ\\
\int_{a}^{b} p(x) dx = 1\\
q(x) = 1/(b-a)\\
(x \in [a,b])\\
そして $q(x)$ を基準とした $p(x)$ のKullback-Libler情報量
kl(p,q) = -\int_{a}^{b}p(x)log_2(p(x)/q(x)) dx
の値が乱数発生数に対してどんな変化をするか調べてみた。
なお、この $kl(p,q)$ を標語的に言うならば「どこが零点になるか分からない確率分布」と「関数 $f$ の零点候補の確率分布」の違いを表した指標と言える。
Kullback-Leibler 情報量の変化
乱数発生数を10から1000まで増分10で変化させたときのKullback-Leibler情報量をグラフ化したのが下図である。
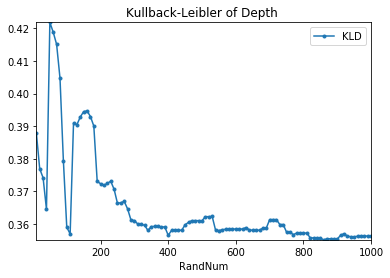
このグラフを見ると、最初は振動が激しいが、400付近から安定的な値になっていることが分かる。
すなわち、乱数発生数をこの後いくら増やしても情報量は増えないのだから、安定したところで打ち切るのが時間の節約になる。そこで、Kullback-Leibler情報量の連続した直近の $N$ 点 $(x_1,x_2,..,x_n)$ について平均値
$\mu$ からの差分 $(x_1-\mu,x_2 - \mu,..,x_n - \mu)$ と $N$ 個の $1$: $(1,1,..,1)$ の相関係数が閾値を超えたら安定と判定して「安定する乱数発生数」を決めることにした。
例えば、$N=3$ 、閾値=$0.5$で安定する乱数発生数を求めると次のように $430$ が安定する乱数発生数になる。
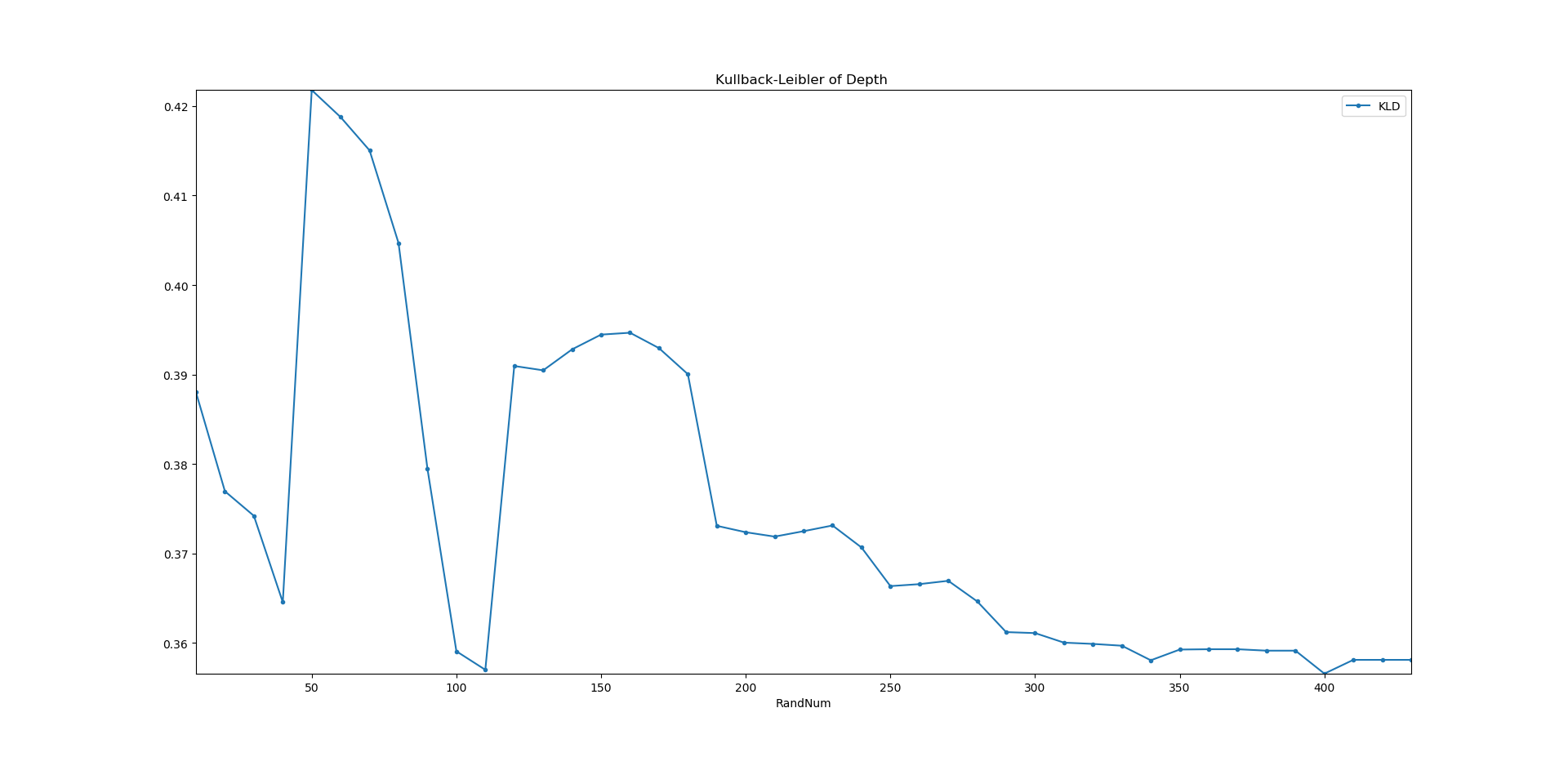
「Good Number of Random Points」とは上の安定する乱数発生数のことだったのである。
深さ計算で ∞ になったら?
深さ計算で結果が∞になることがあるが、それは、$log_{2}f(x)=-\infty$ のときで、つまり $f(x)=0$ と判断してよいときである。この場合には、$x$ は深さのデータには含めずに、零点候補に直接含めることにした。
Pythonコードの実行について
この記事ではWindows10にAnacondaでインストールしたPython3.7.3を使っています。
Spyder3.3.6およびAnacondaプロンプトから実行確認してあります。
また、numpy,pandas,scipy,decimal,matplotlibをimportしていますので、
不足の場合は適宜インストールしてお使いください。
深さ法の実装:DepthMethod.py
零点取得テスト:test_ZeroPt.py
python test_ZeroPt.py
応用(すべての臨界点と最小点/最大点)を求めるテスト:test_CriticalPt.py
python test_CriticalPt.py
コード詳細は下記を参照して下さい。
https://github.com/curvemanjp/glbZero.git
まとめ
関数説明
SearchZeroPtByDepth : 有界区間で連続な一変数実数関数の零点候補を求める。ただし、零点は有限個とする。
""" 引数 """
SearchZeroPtByDepth(
func, """関数オブジェクト"""
func_name,"""関数の名称(途中データを保存するときのフォルダ名になる)"""
start, """定義域区間の開始座標"""
ended, """定義域区間の終了座標"""
rSeed=0, """乱数のseed"""
InitRandNum=10, """乱数発生数の初期値と増分"""
nRandIterMax=200,"""乱数発生繰り返し回数最大"""
nCheckStabilityDegree=3,"""Kullback-Leibler情報量安定度に使う点数"""
thlCorre=0.5, """Kullback-Leibler情報量安定度判定に使う相関係数の閾値"""
LocalIter=500, """局所的探索での繰り返し回数最大"""
nSave=0, """途中データ保存フラグ(0:保存しない/1:保存する)"""
nDisp=0 """途中経過表示フラグ(0:表示しない/1:表示する)"""
)
""" 戻り値 """
# 第一戻り値:リスト形式(要素数は零点候補の数)
EstimateZeroPt """零点候補の座標"""
FunctionValue """零点候補に対する関数値"""
Iteration """局所探索の繰り返し数"""
# 第二戻り値:安定する乱数発生数 """大局的探索の乱数発生数"""
使用例
import numpy as np
from DepthMethod import SearchZeroPtByDepth
f=lambda x:np.sin(x)
Zeros,rdGoodNum=SearchZeroPtByDepth(f,'sin',-4.0,4.0)
"""Good Number of Random Points : 240"""
print(Zeros)
"""
[ EstimateZeroPt FunctionValue Iteration
0 -3.141593 -1.224647e-16 98
1 0.000000 0.000000e+00 99
2 3.141593 1.224647e-16 89]
"""
print(rdGoodNum)
"""240"""
g=lambda x:np.abs((x-1)*(x-8))
Zeros,rdGoodNum=SearchZeroPtByDepth(g,'not-differentiable',-10.0,10.0)
"""Good Number of Random Points : 270"""
print(Zeros)
"""
[ EstimateZeroPt FunctionValue Iteration
0 1.0 0.0 109
1 8.0 0.0 89]
"""
print(rdGoodNum)
"""270"""
from scipy import special
j=lambda x : special.jv(1,x)
Zeros,rdGoodNum=SearchZeroPtByDepth(j,'bessel',-10.0,10.0)
"""Good Number of Random Points : 410"""
print(Zeros)
"""
[ EstimateZeroPt FunctionValue Iteration
0 -7.015587e+00 -1.729753e-16 103
1 -3.831706e+00 -0.000000e+00 103
2 4.545195e-32 2.272597e-32 107
3 3.831706e+00 0.000000e+00 109
4 7.015587e+00 1.729753e-16 103]
"""
print(rdGoodNum)
"""410"""
適用限界
零点付近で急激に変化する関数では零点候補にもれが出てしまうことがある。(今後の課題1参照)
複数の零点が近接している場合に、零点候補からもれが出てしまうことがある。(今後の課題2参照)
今後の課題
- どの程度の急な変化から、零点候補にもれが出るかの定量的な見極める。
- 複数の零点がどの程度の近接すると、零点候補にもれが出るか定量的に見極める。
- 多変数への拡張
- 応用事例の追加
- ソースコードの整備
参考文献
囲い込み法については1を参照。
情報量の理解には2が適している。
- 今野浩・山下浩(1992) 『非線形計画法』(ORライブラリー 6) 日科技連出版社
- 甘利俊一(2017) 『情報理論』筑摩書房