こんにちは.
今回は最近何かと話題になってる Graph Convolutional Networks における,グラフ構造の畳み込みについてまとめました.
[Modeling Relational Data with Graph Convolutional Networks]
(https://arxiv.org/pdf/1703.06103.pdf)
が原著です.
Relationalですので,エッジに関係性を持ったようなグラフのお話ですね.
理論的な説明記事はいくつかネット上で見かけたのですが,イメージ的に理解したかったので,図を交えながら解説します.
ここでは詳しい数学的理論やその後のタスクへの適用には触れませんが,本記事を読むことで,
グラフ構造の畳み込み方を理解する
ことを目的としています.
Graph Convolutional Networks
その名の通り,グラフ構造を畳み込むネットワークです.
畳み込みネットワークといえばまずCNNが思い浮かぶと思いますが,基本的には画像に適用されるものであり(自然言語等にも適用例はあります),グラフ構造にそのまま適用することはできません.
なぜならば,画像はいかなる場合でも周囲の近傍画素というのは8画素であり,画素がグリッド状に並んでいない特殊なディスプレイを想定したりしない限りその前提が崩れることはないからですね.
しかし,グラフ構造における近傍ノードというのは当然データの関係性によってデータ毎に変わってきます.ですから,CNNのように近傍画素を畳み込む,という決め打ちのアーキテクチャでは対応できません.
画像に例えるならば,「隣の画素があったりなかったりする」といった具合です.
と言っても基本的な畳み込みネットワークと概念は変わりませんから、
入力はグラフ構造を持ったデータ
出力はデータの特徴量
となります.
このイメージを持ったまま以下を読んでいただけると,理解しやすいと思います.
グラフ構造
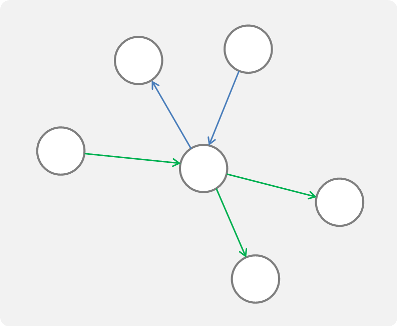
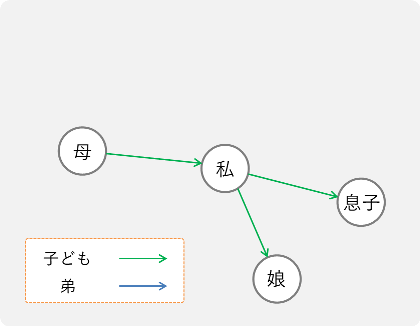
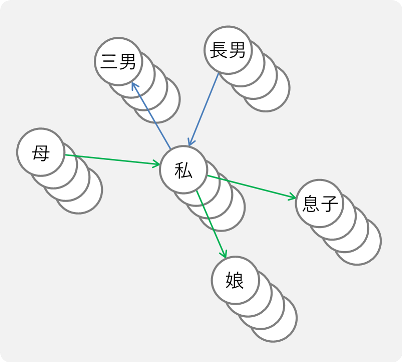
このような有向グラフを考えてみましょう.
今回は載せませんでしたが,双方向な結合やフィードバックループにも適用できます.
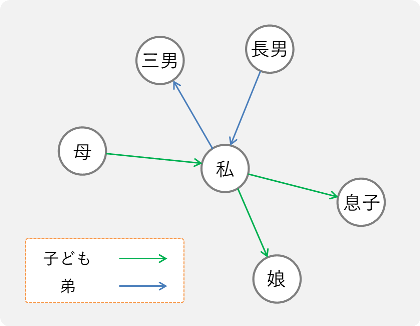
ノードは何かしらの属性,エッジは関係を表していて,例えばこんな例が考えられるでしょう.
このように,グラフ構造で表すことができる世の中の事象ってけっこう多いものです.(有名どころだと,物性予測などの化学系タスクや,顧客の購買データなど)
理論的な説明はこちらのサイトが非常にわかりやすかったです.
グラフ構造を畳み込む
さて,先に述べたグラフを実際に畳み込んで行きます.
一応定義式はこうなりますが.....
h^{(l+1)}_i = \sigma\left( \sum_{r \in \mathcal{R}} \sum_{j \in \mathcal{N}^r_i}\frac{1}{c_{i, r}} W^{(l)}_r h^{(l)}_j + W^{(l)}_0 h^{(l)}_i \right)
数学的理解は後にして,まずイメージから理解していきましょう.
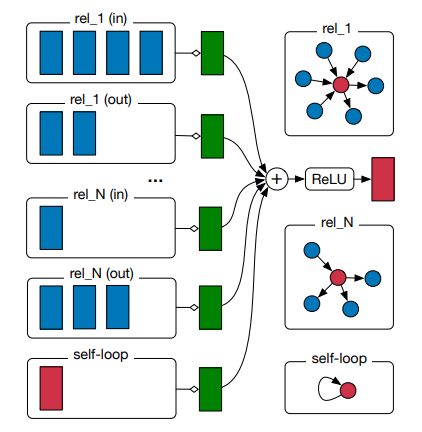
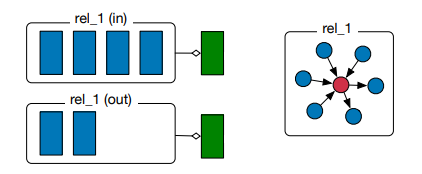
また論文内の説明図は以下のようになっていますが,グラフの全体図が無いため数式が苦手な人にはちょっと意味が掴みにくいです.
この図を噛み砕く形で説明していきます.
イメージ
この論文におけるグラフ構造の畳み込みのポイントを押さえておくと,
1. 各ノードごとに特徴量が抽出される
2. あるノードの畳み込みは,自身と隣接ノードを使って行われる
の2点が分かっていれば,理解が早いです.
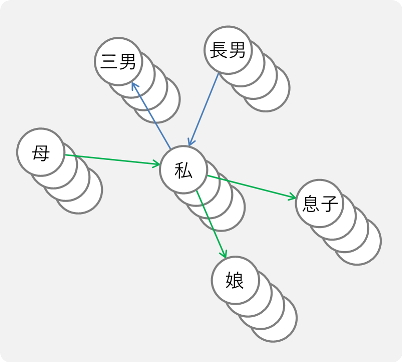
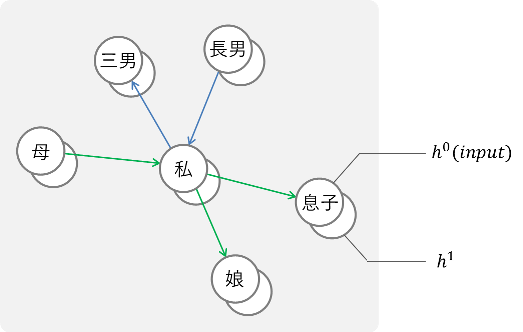
R-GCN層は各ノードそれぞれに適用されるので,例えば1回R-GCN層を通したあとのイメージは以下のような感じですね.
$h_0$ が入力,$h_1$ が第1中間層です.
畳み込みをするごとに,以下のように中間層が増えていくわけです.
では具体的に畳み込みの処理を見ていきましょう.
畳み込む
実際に,先程の図における 私 を畳み込んでいきましょう.
数式は後にするといいましたが,すみません,少しだけ使います.
以下の式は,ノード $i$ における $l+1$ 番目の中間層を表しています.
h^{(l+1)}_i = \sigma\left( \sum_{r \in \mathcal{R}} \sum_{j \in \mathcal{N}^r_i}\frac{1}{c_{i, r}} W^{(l)}_r h^{(l)}_j + W^{(l)}_0 h^{(l)}_i \right)
分かってしまえばシンプルな式で,この2つの $\sum$ に注目すると全体の流れがよくわかります.ちなみに $\mathcal{R}$ が関係(Relation)の集合,$\mathcal{N}^r_i$ が関係 $r$ 下におけるノード $i$ の隣接ノード(インデックス)の集合です.
あるノードにおける畳み込みは,
関係ごとに ( $\sum_{r \in \mathcal{R}}$ ),隣接ノード ( $\sum_{j \in \mathcal{N}^r_i}$ ) を列挙していきます.
そして最後に,自身のノードを使います.
少し数学的に言うと,それぞれを線形結合して活性化関数に通します.
まず,関係 ( $\sum_{r \in \mathcal{R}}$ ) を列挙していきましょう.
例えば今回の図だと,子ども と, 弟 という関係がありますね.
つまるところ私ノードの畳み込みは,
① "子ども" を畳み込む
② "弟" を畳み込む
③ 自身のノードを畳み込む
の,3本立てで行われることになります.
では,順にやっていきましょう.
子どもを畳み込む
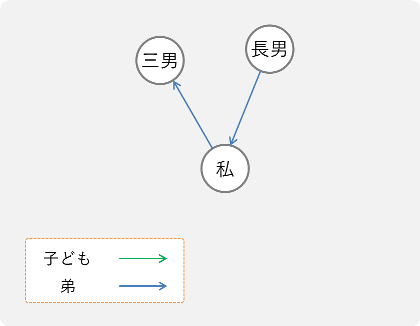
グラフから,子どもの関係だけを抽出します.
このようになりますね.
それぞれの隣接ノードと自分に,重みを掛けて総和を取ってあげるだけです.関係を抽出したあとに抽出されたノードを順次処理するので,$\sum_{j \in \mathcal{N}^r_i}$ なんですね.
(何気なく重みと言いましたが,原著の2.2章で言及されています.スカラー値と基底変換によって表されるのですが,グラフ構造の畳み込みを理解するのが目的の本記事では触れませんので,興味がある方は原著をご覧ください.)
さてここで気をつけたいのは,式だけからは読み取れないのですが同じ関係であっても
"入力と出力は異なる関係として扱う"
という点です.依存関係が異なれば性質も異なるためです.
数式にすると,以下のようになりますね.
なお,$L$はある特徴について線形結合した特徴量ベクトルを表しています.
L_{child\_in} = W_{child\_in}v_{mother} \qquad\qquad\quad\quad\quad\
L_{child\_out} = W_{child\_out}v_{son}+W_{child\_out}v_{daughter}
この時,重み$W$がCNNでいうカーネルに対応していることになります.
論文内の図に対応させると,この部分です.
関係rel_1を抽出し,inとoutに分けて線形結合していますね.
弟を畳み込む
同様に,弟の関係をもったノードを抽出します.
L_{brother\_in} = W_{brother\_in}v_{brother1}
L_{brother\_out} = W_{brother\_out}v_{brother3}
自身のノードを畳み込む
元の定義式における最後の項に注目すると,
W^{(l)}_0 h^{(l)}_i
という記述があります.これが自身のノードに関する畳込みですね.
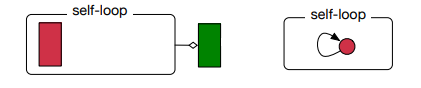
論文中の図のように,自身へのフィードバックループとして解釈します.
普通のCNNと同様,自分自身の情報を含めるのは妥当な定義でしょう.
L_{self} = W_{self}v_{self}
論文内の図で,以下の部分です.
図だけを見てると突然 self-loop が出てきてなんでや,となりますがそういうことです.
まとめる
さて,これで**"私"**のノードを畳み込むことができました.
あとはこれを足し合わせて活性化関数に通すだけです.
先程の3つの操作で得られた $L_{child_in}$, $L_{child_out}$, $L_{brother_in}$, $L_{brother_out}$, $L_{self}$ を使ってR-GCN層を通過したあとの"私"ノードにおける中間層の値を表すと,
h^{1}_{self} = \sigma\left\{ \left( \sum_{r \in \mathcal{R}} \sum_{j \in \mathcal{N}^r_i}\frac{1}{c_{i, r}} W^{0}_r h^{0}_j \right) + W^{0}_0 h^{0}_i \right\} \qquad\qquad\qquad\qquad\qquad\qquad\quad \\
=\sigma \left\{ \left( L_{child\_in}+\frac{1}{2}L_{child\_out}+L_{brother\_in}+L_{brother\_out} \right) + L_{self} \right\}
となり,めでたく中間層の値が計算できました.
さて式についてですが,今は第1中間層の計算を考えているので $h^{0}$ には入力ベクトルが代入されます.
また,$L_{child_out}$に$\frac{1}{2}$の係数がついているのは,$\frac{1}{c_{i, r}}$による正規化係数です.
思い返してみると,"私"から出ていく子供エッジは2本ありました.画像と違いグラフ構造では隣接ノード数がデータによって異なるので,隣接ノード数で割って正規化することでどんなグラフ構造でも統一的に畳み込むことができるようになっています.今回は$c_{i, r}=|\mathcal{N}^r_i|$ ですが,定義によって変更は可能です.
これらの操作を全てのノードに対して適用することで,各ノードにおける中間層の値が求まります.
繰り返しになりますが,以下のグラフにおける $h_1$ を求めることができました.
こんなかんじです.
層を重ねると
追加でR-GCN層を重ねるときは,通常のNNと同じく再帰的に中間層の値を使っていくことで実現します.
複数回畳み込むとこんなイメージ.
先程の演算から分かる通り,1回の畳み込み演算によって隣接ノードの情報が付加されます.
ということは,さらに畳み込めば既に隣接ノードの情報を含むノードを入力として取ることになるので,2回の畳込みによって近傍2ノードの情報を得ることになります.畳み込むほど,局所的な特徴から大局的な特徴になるCNNと同じ流れですね.
まとめ
Graph Convolutional Networksにおける,R-GCN層によるグラフ構造の畳込みについて説明しました.画像をグラフ構造と捉えれば画像タスクにも適用できることから,NNの畳み込み演算において上位の概念であるといえます.
最近(執筆:2018/6/15)DeepMindがGraph Networksの手法を統一化したりだとか,10億単位のノードをもつグラフを学習した論文が出たりと,Graph Networksがちょっと熱いです.
これまでは化学物質の構造に対して適用されることが多かったですが,顧客の行動予測であったり,3D空間上のタスクであったり,他のドメインへの適用が期待されますね.