特徴選択

この記事の狙い・目的

機械学習を取り入れたAIシステムの構築は、
①データセット作成（前処理）→ ②モデルの構築 → ③モデルの適用
というプロセスで行っていきます。
その際「データセット作成（前処理）」の段階では、正しくモデル構築できるよう、事前にデータを整備しておくことが求めらます。
このブログでは、前処理工程で用いられる「特徴選択」の手法について解説していきます。

特徴選択とは

無用な特徴量は予測精度の低下や計算コストの増加を招く恐れがあるため、特徴選択により、多数の特徴の中から、目的とする予測に関連が強い特徴を取捨選択することが求められます。
この記事では特徴選択の主なアプローチについて解説していきます。

特徴選択のメリット

特徴選択のメリットについて触れておきましょう。主なメリットには下記があります。
・目標変数の予測精度向上
　目的変数との関係性をより的確に説明する特徴量を無駄なく選択しモデルに学習させることで、未知のデータに対しての予測誤差を最小にする、つまり予測性能（汎化性能）の向上を測ることができるようになります。
・学習結果の解釈性の向上
　得られたモデルによる推論結果を人間が理解でき、根拠を説明可能であることは、ビジネス上で重要な価値があります。
　例えば、サービスを提供する事業者としての説明責任を果たさなければならないシーンなどです。
　また開発者視点では、モデルのデバッグや精度改善の際に、説明変数のチェックが容易になる、エラー解析の根拠が明確になるなどのメリットがあるでしょう。
・計算効率の向上
　無駄なデータの学習コストを減らすことで、処理時間を減らすことができます

プログラムの実行環境

Python3
MacBook pro（端末）
PyCharm（IDE）
Jupyter Notebook（Chrome）
Google スライド（Chrome）

データセット

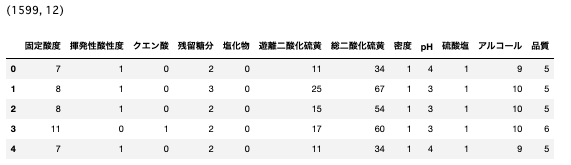
アプローチの解説を行う前に、今回使用するデータセットについて少し触れておきます。
データセット：Machine Learning Repository - UCI

import pandas as pd

# データ取得
wine_red = pd.read_csv("./winequality-red.csv", sep=',')

# データ確認
wine_red.shape
wine_red.head()

特徴選択のアプローチ

今回は特徴選択のアプローチとして以下の４つの手法について解説していきます。
1.統計量を用いた特徴量選択
2.反復特徴量選択法
3.手法ベース特徴量選択法

それでは具体的にひとつずつ見ていきましょう。

1.統計量を用いた特徴量選択

特徴量選択のアプローチとして、まずは変数同士に相関関係があるのか否を確認することが肝要です。相関がある場合とない場合でその後のアプローチが変わってくるためです。
ここでは変数同士の相関関係の強さを表す「相関係数」という指標を用いた特徴選択の手法について紹介します。目的変数に対する相関係数の上位の特徴量を選択するという手法です。
ただし前提として、変数同士にどのような相関関係があるのかを正しく捉えられているかが重要です。一見相関係数が低いものの中にも（実際は）相関性のある変数があったり、反対に、**擬似相関（見せかけの相関）**の変数があったりするためです。
**擬似相関（見せかけの相関）**とは、一見相関係数の高い変数同士に、実際には（直接的な）関係がないもののことを言います。
この見極めには、ドメイン知識があれば検知できることが実際は多いかもしれませんが、統計学的に求められた相関係数が妥当であるかを検定する手法なども存在するため、この記事で少し触れておきたいと思います。
また、検定結果の考察のためには、そもそも相関係数がどのような仕組みで求められているかを理解していることが欠かせません。
よって、以下では相関係数、特に「ピアソンの積率相関係数」「スピアマンの順位相関係数」とそれぞれに対する考察、および各係数を用いた特徴選択の方法についてまずは解説していきます。
まずは散布図行列で描画して、データ同士の関係を見てみましょう。
（蛇足ですが、特徴量同士の疑似相関は主成分分析などで取り除くか、ロバストなモデルを利用することで解決を図るのも手だと思います。）

pd.plotting.scatter_matrix(wine_red, c='blue', figsize=(20, 20));

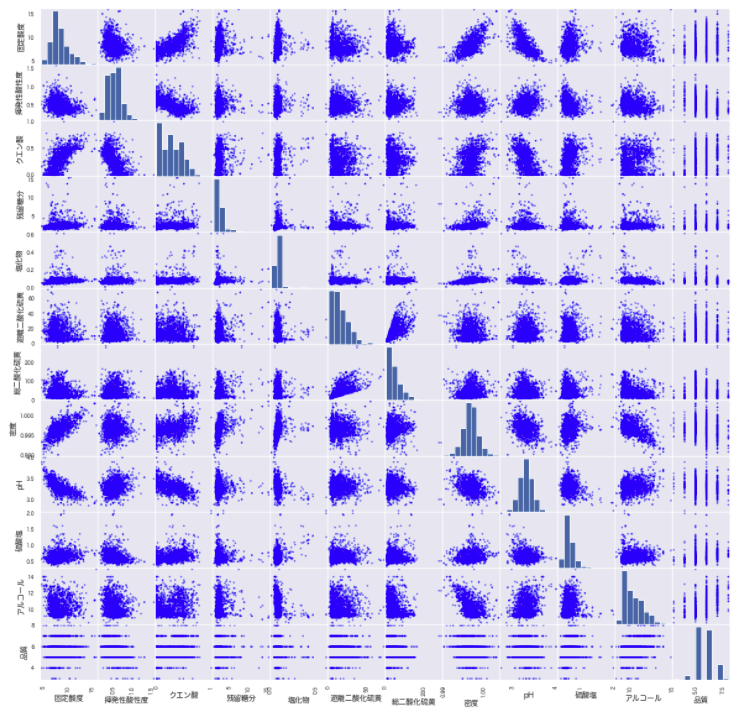
強い線形関係の変数はなさそうです。ただし、おおよそ同一方向に増減をしている変数があり、低〜中程度に相関のある項目はありそうです。
本来いろいろなグラフなどを用いて考察していく工程がありますが、記事の流れの関係上、以下では相関係数とその考察方法から解説させていただきます。

①ピアソンの積率相関係数を用いた手法

ピアソンの積率相関係数とは、2つの量的変数間の直線的関連の程度を表す係数のことです。
一般的に「相関係数」と言うと、この「ピアソンの積率相関係数」のことを指します。
$n$組のデータ$(x_1,y_1),(x_2,y_2),…,(x_n,y_n)$ があり、それぞれの平均 $ \overline x , \overline y $ としたとき、ピアソンの積率相関係数$r_{xy}$は以下の式で表されます。

r_{xy} = \frac{\sum_{b=1}^{N}(x_i - \overline x)(y_i - \overline y)}{\sqrt{\sum_{b=1}^{N}(x_i - \overline x)^2}\sqrt{\sum_{b=1}^{N}(y_i - \overline y)^2}} = \frac{s_{xy}}{s_xs_y}

つまり、ピアソンの積率相関係数r_xy は，「変数X と変数Y の共分散」÷「それぞれの変数の標準偏差」の式で求められます。

・考察方法
前提として「相関係数p>0」は正相関、「相関係数p<0」は負相関、「相関係数p≒0」は無相関を表します。
注意点としては、どちらか一方の変数の分散が0の時、相関係数を定義できません。値に変化がないものとの相関は測ることができません。
また、ピアソンの積率相関係数は母集団が正規分布を仮定した手法のため、現実の多くのデータに不適切なケースがままあります。
ピアソンの積率相関係数は「線形な関係があるかどうか」を確認することができます。
まずはデータの外形をグラフで確認してから、（ピアソンの積率）相関係数を求めていくと良いでしょう。

・メリット
全てのデータの大小関係を考慮できることから、間隔尺度・比率尺度の状態を保持して関係性を考察できる。
・デメリット
ある変数が外れ値含む場合、標準偏差、分散式はすべての値を計算に含めるため、その結果が外れ値の影響を（強く）受ける
この場合は、外れ値を事前に処理するか、順位相関係数を用いるかなどの検討が必要でしょう。詳しくは後述します。

# ピアソンの積率相関係数
pearson=wine_red.corr(method='pearson') # 'pearson'
pr_corr_df = pd.DataFrame()
pr_corr_df = pearson.round(decimals=3).astype(str)
pr_corr_df

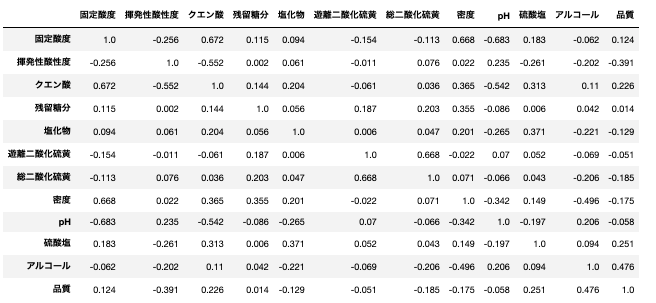
「pH⇆固定酸度」の相関係数が[-0.683]から、中程度の負の相関があることがわかる。

# ピアソンの積率相関係数（自装してみた）
def pearson_corr(x, y):
    x_diff = x - np.mean(x)
    y_diff = y - np.mean(y)
    return np.dot(x_diff, y_diff) / (np.sqrt(sum(x_diff ** 2)) * np.sqrt(sum(y_diff ** 2)))

corr = pearson_corr(wine_red['pH'], wine_red['固定酸度'])
corr

# 結果：-0.6829781945685298

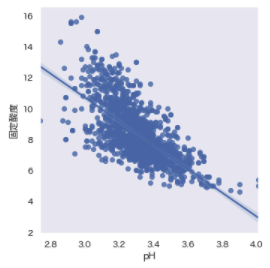
# 二変数を描画
plt.figure(figsize=(5,5))
sns.regplot(x=wine_red['pH'], y=wine_red['固定酸度'])
plt.tight_layout()
plt.show()

完全ではないが同方向の関係性が見て取れます。

②スピアマンの順位相関係数を用いた手法

スピアマンの順位相関係数は、順位相関係数の一種で、各変量を順位に変換してピアソンの積率相関係数を求めたもののことです。
具体的には、以下の通りです。
1.対になった変数XとYがn対あるとき、それぞれで順位を求める。
2.n対すべてについて、$i$番目のデータ$X_i$と$Y_i$の順位の差$d_i$を求め、次の式から順位相関係数$r_s$を算出する

r_2 = 1 - \frac{6\sum_{i=1}^{N}d_i^2}{n(n^2 - 1)}

・考察方法
端的には、スピアマンの順位相関係数は「一緒に変化するかどうか」を確認することができます。

・メリット
ピアソンの積率相関係数と違い、母集団の特定の分布仮定しないため、現実の多くのデータに対して有効な分析手法です。
順位付けを行う過程で、各順位間の大きさが均一となるため、外れ値の影響を受けなくなります。
・デメリット
メリットの裏返しですが、順位同士の差が均一化されることで、もともとあった「大小関係の程度」は失われてしまいます。
つまり、順位付けを行うため、順序尺度のデータに対して有効な手法であることに注意が必要です。（間隔尺度・比率尺度ではなく）

# スピアマンの順位相関係数
spearman=wine_red.corr(method='spearman') # 'spearman'
sp_corr_df = pd.DataFrame()
sp_corr_df = spearman.round(decimals=3).astype(str)
sp_corr_df

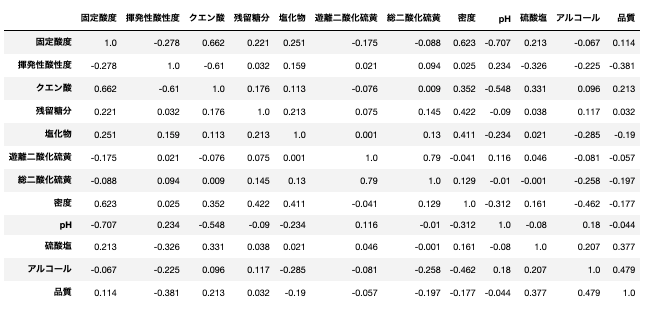
遊離二酸化硫黄⇆総二酸化硫黄」の相関係数が[0.668→0.79]に上がっている。可視化して確認してみる。

plt.figure(figsize=(5,5))
sns.regplot(x=wine_red['遊離二酸化硫黄'], y=wine_red['総二酸化硫黄'])
plt.tight_layout()
plt.show()

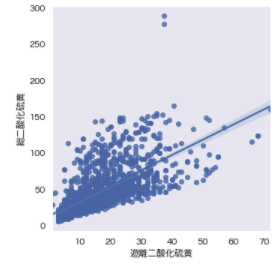
多少発散した分布となっていますが、ある程度同方向の関係性が見て取れます。
蛇足ですが、外れ値を含んでいそうなため、除去すべきか検討が必要と思われます。

相関係数の有意性の検証方法

前提として、ピアソンの積率相関係数が有意かどうかを調べる場合は、２つの変数の同時分布が「2変量正規分布」に従うこと、つまり2つの変数がそれぞれ正規分布に従うのかを調べておく必要があります
簡単な方法としては、ヒストグラムで外形を確認する方法があります。この時更に、得られたデータから平均と分散を計算して、平均と分散を計算してそれらをパラメータにする理論的な正規分布とヒストグラムを比較できると尚良いでしょう。

# 平均と分散
ph_mean = np.mean(wine_red['pH'])
ph_mean
ph_var = np.var(wine_red['pH'])
ph_var
import math
ph_std = math.sqrt(ph_var)
ph_std

# 平均：3.311113195747343
# 分散：0.023820274241131745
# 標準偏差：0.15433818141060152

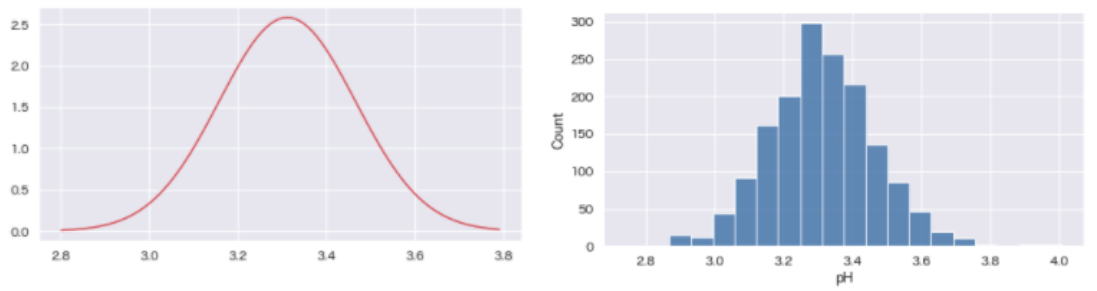
# 平均と分散から正規分布のグラフを作成
from scipy.stats import norm

# 2.8から3.8まで、0.01間隔のリストXを生成
X = np.arange(2.8,3.8,0.01)

# 確率密度関数Xに、平均=ph_mean、標準偏差=ph_stdを代入
Y = norm.pdf(X, ph_mean, ph_std)

# 正規分布をプロット
plt.figure(figsize=[8,4])
plt.plot(X,Y,color='r')
plt.grid()
plt.show()

plt.figure(figsize=[8,4])
plt.grid()
sns.histplot(wine_red['pH'], bins=20);

もう一つ、**QQプロット（qqnorm）**を使う方法もあります。これは、正規分布の累積分布関数を用いる方法です。
累積分布の25%点と75%点を結び、その直線上にデータが分布するかを確認することで、正規分布と近似するかどうかを判断することができます。

# 描画、確認
import scipy.stats as stats

def qqplot(dist):
    plt.figure(figsize=[8,4])
    plt.hist(dist, bins=30)
    plt.grid()
    plt.show()
    
    plt.figure(figsize=[8,4])
    stats.probplot(dist, dist="norm", plot=plt)
    plt.grid()
    plt.show()

qqplot(wine_red['pH'])

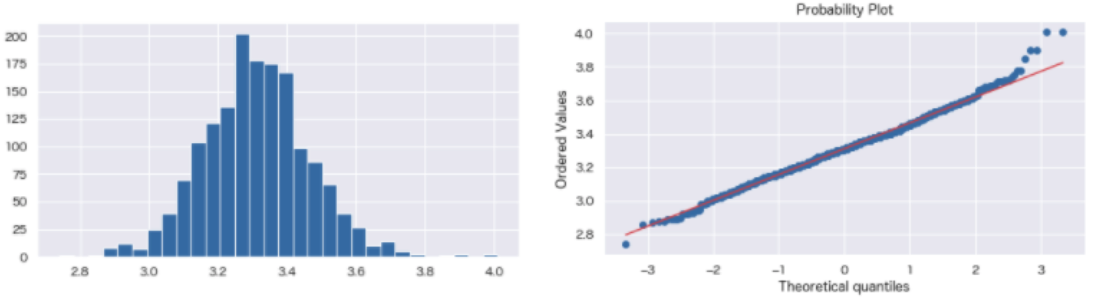
右側のグラフがQQプロットです。累積分布の25%点と75%点の直線上に、おおよそ分布しており、正規分布に近いと思われます。

統計的に正規分布を確かめたい場合は「コルモゴロフ・スミルノフ検定」という検定手法がありますが、ここでは割愛させていただきます。

無相関検定

ここまでの解説した方法で「正規分布か否か」を確認することができました。
いよいよ相関係数の（有意性）検定の手法を見ていきましょう。
相関係数の検定手法もケースバイケースで多くの手法があるのですが、今回は「母相関係数の無相関検定」を紹介したいと思います。
「母相関係数の無相関検定」を用いれば、標本では相関がある場合に、母集団でも同様に相関があるかどうかを確認することができます
仮説は以下とします。
「帰無仮説：母相関係数は0である（無相関）」
「対立仮説：母相関係数は0でない（相関あり）」
ｐ値＜有意水準0.05　（5％）で帰無仮説を棄却、対立仮説を採択することとします。
検定統計量tは下記の式で求めていきます。$n$はサンプルサイズ、$r$は単相関係数を表します。
検定統計量は自由$ｎ－2$のｔ分布にしたが

t = r\sqrt{\frac{n- 2}{1 - r^2}}

from scipy.stats import pearsonr, spearmanr

# pH と 密度について無相関検定を実施する
ph = wine_red['pH'].values
density = wine_red['密度'].values

# ピアソンの相関係数とp値を計算する。
result = pearsonr(ph, density)
# 結果
r_value = result[0]
p_value = result[1]
print('相関係数：', r_value)
print('p値：', p_value)

print('='*30)

# スピアマンの相関係数とp値を計算する場合
result2 = spearmanr(ph, density)
# 結果
r_value2 = result2[0]
p_value2 = result2[1]
print('相関係数：', r_value2)
print('p値：', p_value2)

どちらも、p値 < 有意水準（0.05）であるため帰無仮説は棄却され（対立仮説が採択され）、有意な相関ありと判定できそうです。

上記以外にも「相互情報量」という、母集団に正規分布を仮定しない、非線形な相関関係も検出できる手法がありますが、今回は割愛させていただきます。

選択した特徴量と相関係数の高い他の特徴量がある場合のアプローチ

こちらのケースも注意が必要です。
選択した特徴量と相関係数の高い特徴量がある場合は、片方を削除する、または交互作用特徴量を生成する、ビニングで二変量の統計量で特徴量を生成する、などの方法が有効な場合があります。
交互作用特徴量、およびビニングについては、以下で解説しています。参考にしてください。

2.反復特徴量選択法

反復特徴量選択法とは、説明変数を増やしたり減らしたりを繰り返して予測精度を推し量りながら特徴量を選択する手法です。
もちろん全ての変数に対してこの作業をすることもできますが、それでは効率が悪く、結果の数値的な変化しか捉えられず根拠の乏しい対応となってしまうでしょう。
そのため、前提として「1.統計量を用いた特徴量選択」で相関関係の有無、強さを推定済みであることが望ましいでしょう。
以下で「変数増加法」「変数減少法」について簡単に触れておきます。

変数増加法（前方選択法）

前方選択とは、求められた特徴量重要度の高いものから一つずつ特徴量をデータセットから追加し、予測精度を測る手法です。

変数減少法（後方削除法）

後方削除は（前方選択と反対で）求められた特徴量重要度の低いものから一つずつ特徴量をデータセットから取り除き、予測精度を測る手法です。

・メリット
どんな回帰分析手法とも組み合わせることができる。
特徴量を追加・削除するシンプルな手法のため、特段、利用制限などはありません。
・デメリット
回帰モデルの構築を繰り返す回数次第で、処理コストが増大してしまう。

# 変数減少法
from sklearn.feature_selection import RFE
from sklearn import linear_model
from sklearn.preprocessing import normalize

X = wine_red.drop(columns='品質', axis=1)
y = wine_red['品質']

X_norm = normalize(X, norm='l2')
rfe = RFE(estimator=linear_model.LinearRegression(), n_features_to_select=5)
rfe.fit(X_norm, y)
rfe_features = pd.DataFrame(X_norm, columns=wine_red.columns[:-1]).loc[:, rfe.get_support()].columns.tolist()

print(f'重要度が上位5件の特徴量： {rfe_features}')

# 結果： 重要度が上位5件の特徴量： ['pH' '塩化物' '密度' '揮発性酸性度' '硫酸塩']

3.手法ベース特徴量選択法

最後にアルゴリズムを用いて、正解ラベルと各特徴量の関係から、特徴量重要度（feature_impotance）を求める方法とについて解説していきます。
ただし、アルゴリズムを用いた手法は、アルゴリズム内部の計算式なども複数パターンあり、正しく考察するためにはその理解が欠かせません。よって、それぞれの特徴と計算方法について特に触れていきたいと思います。

①決定木ベース（ランダムフォレスト、勾配ブースティング）を用いた例

仕組み
簡単に言えば、各特徴量x_jを外した時に、予測精度（正解率）がどれくらい悪化するかを求め、その差で重要度を推定する方法です。
計算過程のイメージは下記の通りです。

1.データサンプル N 個のうち n(<N) 個をランダムに抽出して決定木を1つ作る。選ばれなかった N−n 個のデータサンプルを OOB (out-of-bag) と呼びます。
2.OOB に対する性能（正解率）a を算出する。
3.OOB のデータサンプル内で、特徴量 xj の値だけをランダムシャッフルで除外し、その状態で決定木の性能（正解率）aj を算出する。
4.1~3の繰り返し

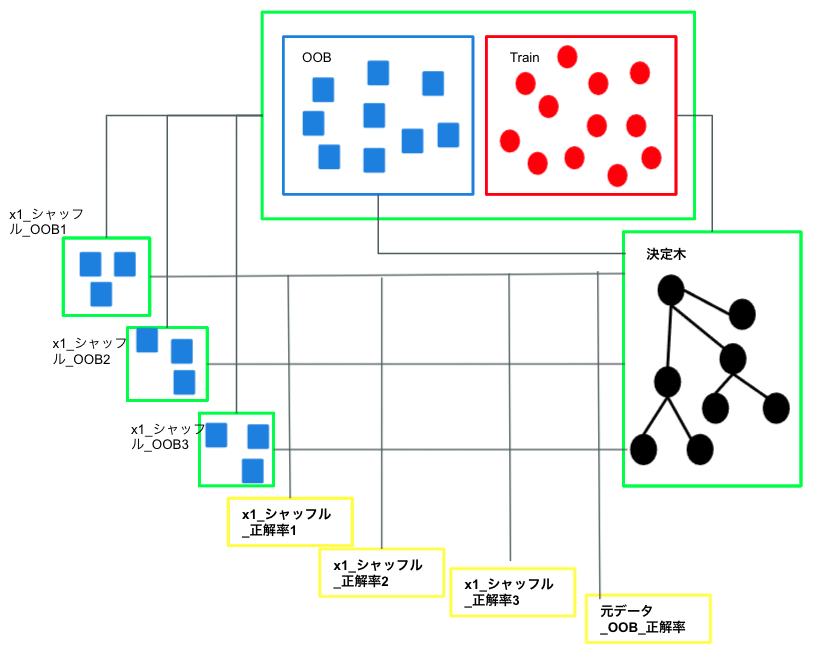
それでは実装を見ていきましょう。

from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.ensemble import RandomForestClassifier

# データ分割
X = wine_red.drop(columns='品質', axis=1)
y = wine_red['品質']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# モデリング
clf_rf = RandomForestClassifier()
clf_rf.fit(X_train, y_train)
y_pred = clf_rf.predict(X_test)

# 評価
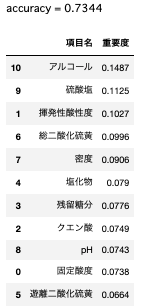
accu = accuracy_score(y_test, y_pred)
print('accuracy = {:>.4f}'.format(accu))

# 重要度
fimp = clf_rf.feature_importances_

# データフレームに変換
imp_df = pd.DataFrame()
imp_df['項目名'] = wine_red.columns[:-1]
imp_df['重要度'] = fimp.round(decimals=4).astype(str)
imp_df.sort_values(by='重要度', ascending=False)

勾配ブースティング（XGBoost、LightGBM）を用いた例

勾配ブースティングは計算方法が２つあります。
「モデルの学習の際、その特徴量が使用された回数」で推定する方法（split）
「その特徴量が使用される分岐から、どれくらいトレーニングデータに対して損失関数を小さくなったか（目的関数がどれだけ改善されたか）の幅」で推定する方法（gain）※XGBoostはsplitはなし。
デフォルトではsplitとなっていますが、そもそも論として木の分岐ごとに重要度は異なるため、使用頻度だけを見るのは特徴選択の根拠としては弱いと思われます。
パラメータ「importance_type= splite or gain」で制御します。

・メリット
計算仮定を可視化できる。
・デメリット
特徴量同士で相関の強い変数が含まれる場合、重要度が低くでやすい。

# XGBoost
import xgboost as xgb

# データ分割
X = wine_red.drop(columns='品質', axis=1)
y = wine_red['品質']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# パラメータ
xgb_params = {"objective": "reg:linear", "eta": 0.1, "max_depth": 6, "silent": 1}
num_rounds = 100

# XGBoost用のデータセットの作成
dtrain = xgb.DMatrix(X_train, label=y_train)

# 学習
gbdt = xgb.train(xgb_params, dtrain, num_rounds)

# 重要度
_, ax = plt.subplots(figsize=(12, 4))
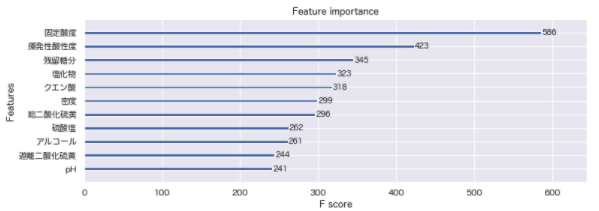
xgb.plot_importance(gbdt, ax=ax, importance_type='gain') # gain: 予測精度をどれだけ改善させたることができるできたか（平均値）

# 生成された全ての木の中にその変数がいくつ分岐として存在するか（平均値）
_, ax = plt.subplots(figsize=(12, 4))
xgb.plot_importance(gbdt, ax=ax, importance_type='weight')

#　LightGBM
import lightgbm as lgb

def lightgbm_learning(imp_type):
    # データ分割
    X = wine_red.drop(columns='品質', axis=1)
    y = wine_red['品質']
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

    # パラメータ
    lgb_params = {"objective": "regression", "eta": 0.1, "max_depth": 6, "importance_type": imp_type}
    num_rounds = 100

    # LightGBM用のデータセットの作成
    dtrain = lgb.Dataset(X_train, label=y_train)

    # 学習
    lgbdt = lgb.train(lgb_params, dtrain, num_rounds)
    
    return lgbdt

# 重要度の可視化
def plot_feature_importance(df):
    n_features = len(df)
    df_plot = df.sort_values('重要度')
    f_importance_plot = df_plot['重要度'].values
    plt.figure(figsize=[10,4])
    plt.barh(range(n_features), f_importance_plot, align='center') 
    cols_plot = df_plot['項目'].values
    plt.yticks(np.arange(n_features), cols_plot)
    plt.xlabel('特徴量重要度')
    plt.ylabel('項目')

# 学習
lgbdt = lightgbm_learning(imp_type='split')

# 特徴量重要度の算出
cols = list(wine_red.drop('品質',axis=1).columns)
f_importance = np.array(lgbdt.feature_importance())
df_importance = pd.DataFrame({'項目':cols, '重要度':f_importance})
df_importance = df_importance.sort_values('重要度', ascending=False)
display(df_importance)

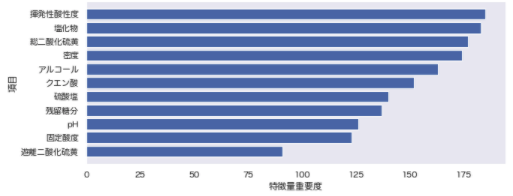
# 重要度の可視化
plot_feature_importance(df_importance)

②回帰系（Lasso回帰、Ridge回帰、ロジスティック回帰）の例

Lasso回帰、Ridge回帰、ロジスティック回帰では、回帰係数（重み）から重要度を算出することができます。
メリット
回帰係数により計算しているため結果の要因分析を行いやすい。
デメリット
多重共線性のある特徴量に対しては重要度を正しく計測できないことがある。

from sklearn.linear_model import Ridge, RidgeCV, ElasticNet, LassoCV, LassoLarsCV
from sklearn.model_selection import cross_val_score

X = wine_red.drop(columns='品質', axis=1)
y = wine_red['品質']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

def rmse_cv(model):
    rmse= np.sqrt(-cross_val_score(model, X_train, y_train, scoring="neg_mean_squared_error", cv = 5))
    return(rmse)

# model_ridge = Ridge().fit(X_train, y_train)
model_lasso = LassoCV().fit(X_train, y_train)
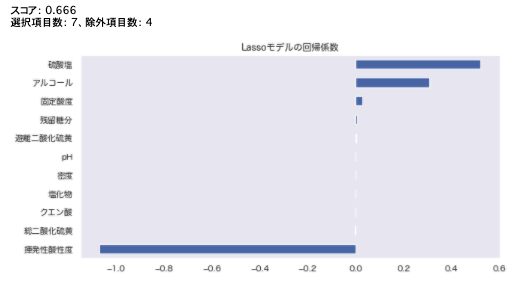
print(f'スコア： {rmse_cv(model_lasso).mean().round(decimals=3)}')

coef = pd.Series(model_lasso.coef_, index = X_train.columns)
print("選択項目数： " + str(sum(coef != 0)) + "、除外項目数： " +  str(sum(coef == 0)))
  
plt.figure(figsize=[10,5])
imp_coef = coef.sort_values()
imp_coef.plot(kind = "barh")
plt.title("Lassoモデルの回帰係数");

# ロジスティック回帰
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import MinMaxScaler 
from sklearn.linear_model import LogisticRegression

# データ分割
X = wine_red.drop(columns='品質', axis=1)
y = wine_red['品質']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# パイプライン化
pipe_lr = make_pipeline(MinMaxScaler(), LogisticRegression(max_iter=1000, C=5.0))
pipe_lr.fit(X_train, y_train)

# 予測、評価
y_pred = pipe_lr.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f'正解率： {accuracy}')
print("="*20)

# 回帰係数
print("回帰係数")
for col in np.argsort(pipe_lr.steps[1][1].coef_[0])[::-1]:
    print("{0}: {1}".format(X.columns[col], pipe_lr.steps[1][1].coef_[0][col].round(decimals=3)));

# 回帰係数
coef = pd.Series(pipe_lr.steps[1][1].coef_[0], index = X_train.columns)
imp_coef = coef.sort_values()
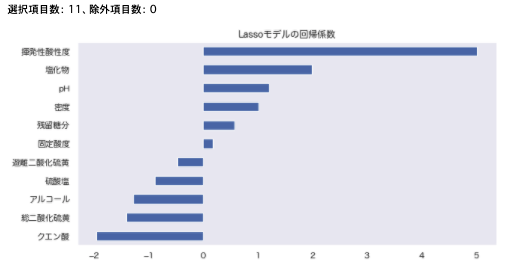
print("選択項目数： " + str(sum(coef != 0)) + "、除外項目数： " +  str(sum(coef == 0)))

# 可視化
plt.figure(figsize=[10,5])
imp_coef.plot(kind = "barh")
plt.title("Lassoモデルの回帰係数");

まとめ

これまでなんとなく行っていた重要度の推定について、アルゴリズムごとの特性や計算方法についてまとめることができ、今後自分でアルゴリズムを構築していくための基礎になると感じました。
論文を読みながら古典なアルゴリズムよりも精度の高いアルゴリズムを作れるようになりたいと思います。

最後に

他の記事はこちらでまとめています。是非ご参照ください。

参考文献

筑波大学 - 機械学習 特徴選択とL1正則化 - 佐久間　淳
参議院 - 回帰分析におけるｔ値とｐ値の意味について - 前田 泰伸
大阪経済大学 - 相関係数に関する若干の考察 - 相関係数に関する若干の考察
安全性評価研究会 - 統計一口メモ　第13話 「相関をｐ値で見てはダメ！」
データ生成過程の学習:因果推論・特徴選択へのアプローチ

解析結果

実装結果：GitHub/wine_quality_select.ipynb
データセット：Machine Learning Repository - UCI

参考資料