概要 / Overview
Prologで2桁×2桁の虫食い算を自動で解くGUIアプリの紹介。
Introducing a GUI app that automatically solves 2-digit × 2-digit cryptarithms using Prolog.
導入 / Introduction
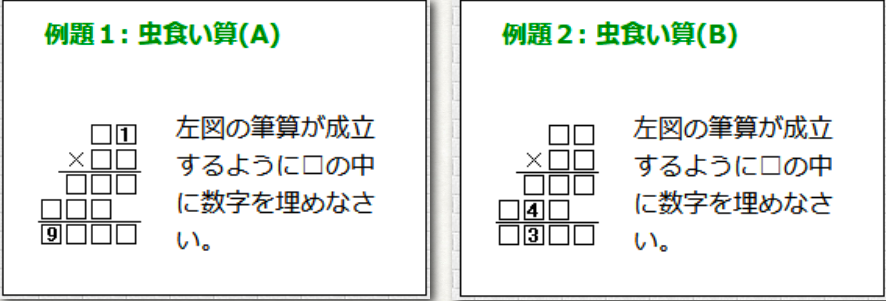
虫食い算という算数の問題をご存知でしょうか?
Have you ever come across a math puzzle called a cryptarithm?
以下に2桁かける2桁の虫食い算の例を挙げます。
Here’s an example of a 2-digit × 2-digit cryptarithm.
これについて「どんな2桁かける2桁の虫食い算でも自動で解けるプログラムを作りなさい」と言われたらどうでしょうか?
Now imagine being asked to write a program that can automatically solve any 2-digit × 2-digit cryptarithm.
結構めんどくさそうですよね?
Sounds tricky, doesn’t it?
本記事では、プログラミング言語「Prolog」を使ったら、2桁かける2桁の虫食い算を自動で解けるプログラムを簡単に作れた!という体験談を通じて、Prologのすごさをお伝えします。
In this article, I’ll share how I easily built a program that solves these puzzles using the programming language Prolog — and how it revealed just how powerful Prolog can be.
Prologについて / About Prolog
まずは、Prologがどんな言語かを簡単に紹介します。
Let’s begin with a brief introduction to what Prolog is.
書籍「7つの言語 7つの世界」(Bruce A. Tate 著, まつもと ゆきひろ 監訳, 田和 勝 訳, オーム社, 2011年)」からそのまま引用させてもらいます。
The following quotes are taken directly from the book Seven Languages in Seven Weeks.
- Prologは、Alain Colmerauer氏とPhillippe Rousell氏によって1972年に開発された論理プログラミング言語で自然言語処理の世界で広く使われている。
- ルールベース言語であるPrologを使えば、論理を表現したり質問をしたりできる。
- SQLと同様にPrologはデータベースを扱うが、データは論理ルールと関係から成る。また、やはりSQLと同様に2つの部分、すなわちデータを表現する部分とデータに質問する部分で構成される。
- Prologでは、データは論理ルール形式で記述する。
以下にPrologの構成要素を示す。
- 事実
特定の世界についての基本的な表明
(「ベーブは豚である」、「豚は泥が好きである」など)- ルール
その世界の事実に関する推論
(「動物が豚であれば、その動物は泥が好きである」など)- 質問
その世界に関する質問(「ベーブは泥が好きか?」など)- 事実とルールは知識ベースを形成する。
- Prologのコンパイラは、質問が効率的に処理できる形式に知識ベースをコンパイルする。
そんなPrologを使うと、例えばこんなことができます。
Here’s an example of what Prolog can do.
地図の塗り分け問題 / Map Coloring Problem
引き続き同書籍から引用させてもらいます。
Continuing with another example from the same book.
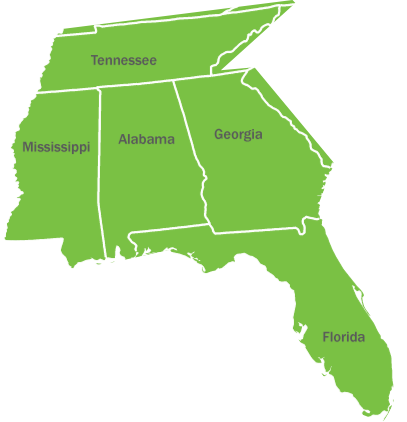
以下の図「アメリカ南西部の州」の、5つの隣接する州が同じ色にならないように3色で塗り分けたいとします。
Let’s try to color the southwestern United States using three colors so that no two neighboring states share the same color.
この問題をPrologで解くために、単純な事実関係をコーディングします。
We can encode the problem in Prolog using simple facts.
- Prologプログラム(地図の塗り分け) / Prolog Program (Map Coloring)
different(red, green). different(red, blue).
different(green, red). different(green, blue).
different(blue, red). different(blue, green).
coloring(Alabama, Mississippi, Georgia, Tennessee, Florida) :-
different(Mississippi, Tennessee),
different(Mississippi, Alabama),
different(Alabama, Tennessee),
different(Alabama, Georgia),
different(Alabama, Florida),
different(Georgia, Florida),
different(Georgia, Tennessee).
最初の3行で塗り分けに使う異なる2色の組み合わせを指定しています。
The first three lines specify which pairs of colors are considered different.
- 赤の隣は緑。もしくは青。 / Red can be next to green or blue.
- 緑の隣は赤。もしくは青。 / Green can be next to red or blue.
- 青の隣は赤。もしくは緑。 / Blue can be next to red or green.
以降の行に塗り分けのルールを記載しています。
he remaining lines define the adjacency rules for each state.
- ミシシッピ州とテネシー州は違う色かつ、
- Mississippi and Tennessee must have different colors, and
- ミシシッピ州とアラバマ州は違う色かつ、
- Mississippi and Alabama must have different colors, and
- アラバマ州とテネシー州は違う色かつ、
- Alabama and Tennessee must have different colors, and
- アラバマ州とジョージア州は違う色かつ、
- Alabama and Georgia must have different colors, and
- アラバマ州とフロリダ州は違う色かつ、
- Alabama and Florida must have different colors, and
- ジョージア州とフロリダ州は違う色かつ、
- Georgia and Florida must have different colors, and
- ジョージア州とテネシー州は違う色。
- Georgia and Tennessee must have different colors.
上記プログラムをPrologにロード後、Prologに質問すると以下の回答が得られます。
After loading the above program into Prolog, you can ask Prolog a query and obtain the following answer.
- Prolog「地図の塗り分け」実行結果 / Prolog Map Coloring Results
?- coloring(Alabama, Mississippi, Georgia, Tennessee, Florida).
Alabama = blue,
Mississippi = Georgia, Georgia = red,
Tennessee = Florida, Florida = green ;
Alabama = green,
Mississippi = Georgia, Georgia = red,
Tennessee = Florida, Florida = blue ;
Alabama = blue,
Mississippi = Georgia, Georgia = green,
Tennessee = Florida, Florida = red ;
Alabama = red,
Mississippi = Georgia, Georgia = green,
Tennessee = Florida, Florida = blue ;
Alabama = green,
Mississippi = Georgia, Georgia = blue,
Tennessee = Florida, Florida = red ;
Alabama = red,
Mississippi = Georgia, Georgia = blue,
Tennessee = Florida, Florida = green ;
false.
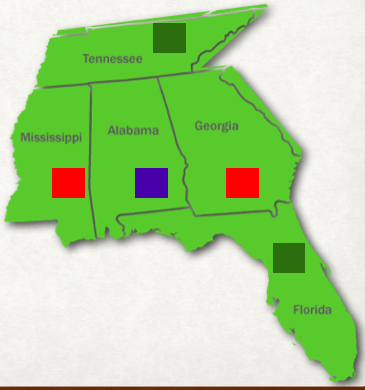
Prolog処理系(実装)「SWI Prolog」の対話環境にて「Alabama, Mississippi, Georgia, Tennessee, Floridaがルール coloringを満たす色は?」と質問したところ、6通りの色の組み合わせが回答されました。(最初は1個だけ回答され、セミコロンを入力して「他には?」と聞くことを繰り返したところ、7回目でfalse.と回答されました。)
When we asked SWI Prolog “Which colors satisfy the coloring rules for Alabama, Mississippi, Georgia, Tennessee, and Florida?”, we received six combinations. (Initially one answer is shown; typing a semicolon asks for more, and after the 7th query, it returns false.)
確認のために1個目の回答を図示します。
Here’s a visualization of the first answer.
Prolog、すごくないですか? おもしろいでしょ?
Pretty amazing, right? Isn’t Prolog fun?
引き続き同書籍から引用します。
Continuing with quotes from the same book.
この5つの州を3色で塗り分ける方法が1つ見つかった。
わずか12行のコードで答えが見つかった。プログラムはどこに?
なんと、アルゴリズムなんか気にしなくて良いのだ。
上の問題をお好みの手続き型言語で解いてみてほしい。
解法はわかりやすいだろうか?このような複雑なロジックを含む問題をRubyやIoで解くための手順を考えてみるとよい。
引き続き引用します。
Continuing the quotes.
例えば次のような手順が考えられる。
ロジックをまとめて整理する。
ロジックをプログラムで表現する。
すべての解法を見つける。
解法をプログラムで実装する。この手のプログラムを何度もそのつど書くことになるだろう。
Prologでは、事実と推論でロジックを表現し、利用者に質問させる。
手順を追った解法を作る必要はない。
Prologでは、論理的な問題を解くためにアルゴリズムを書くことはしない。
現実世界をそのまま記述して、コンピュータが取り組める様な論理的な問題として提示する。
コンピュータに仕事をさせよう!
穴埋め問題の応用 / Application to Fill-in-the-Blank Problems
更に同書籍には「穴埋め問題」というキーワードも出てきました。
Furthermore, the same book also introduces the keyword “fill-in-the-blank problem.”
→Prologを虫食い算にも適用できそうな雰囲気が漂ってきました!
→It’s starting to feel like Prolog could also be applied to cryptarithms!
- Prologプログラム(穴埋め問題) / Prolog Program (Fill-in-the-Blank Problem)
%食品の種別の定義
food_type(velveeta, cheese). %velveetaはチーズ類
food_type(ritz, cracker). %リッツはクラッカー類
food_type(spam, meat). %スパムは肉類
food_type(sausage, meat). %ソーセージは肉類
food_type(jolt, soda). %joltはソーダ類
food_type(twinkie, dessert). %twinkieはデザート類
%種別の風味の定義
flavor(sweet, dessert). %デザート類は甘い
flavor(savory, meat). %肉類は美味しい
flavor(savory, cheese). %チーズ類は美味しい
flavor(sweet, soda). %ソーダ類は甘い
%食品と風味のルール
%食品Xの種別がZで、Zの風味がYであるとき、食品XはYの風味をもつ。
food_flavor(X, Y) :- food_type(X, Z), flavor(Y, Z).
- 穴埋め問題実行例 / Example of Executing a Fill-in-the-Blank Problem
%food_typeが肉類の食べ物は何か?
?- food_type(What, meat).
What = spam ;
What = sausage.
%ソーセージは甘いか?
?- food_flavor(sausage, sweet).
false.
%甘いのは何類か?
?- flavor(sweet, What).
What = dessert ;
What = soda.
%美味しい食べ物は何か?
?- food_flavor(What, savory).
What = velveeta ;
What = spam ;
What = sausage ;
false.
良い感じです!
Looks good!
上記の穴埋め問題を応用して、以下の様な質問に回答できるルールをPrologに書ければ、Prologで2桁かける2桁の虫食い算をできるのでは?
By extending the above fill-in-the-blank problem, we can write Prolog rules to answer questions like the following, making it possible to solve 2-digit × 2-digit cryptarithms in Prolog:
- 質問:4かける9割る10の余りZは?
- Question: What is the remainder Z when 4 × 9 is divided by 10?
回答:6
Answer: 6 - 質問:4かけるY割る10の余りが6になるYは?
- Question: What value(s) of Y satisfy that 4 × Y modulo 10 equals 6?
回答:4か9
Answer: 4 or 9
2桁かける2桁の虫食い算について / Understanding the 2-Digit × 2-Digit Cryptarithm
Prologにルールを伝えるため、虫食い算の仕組みを整理してみましょう。
To express the rules in Prolog, let’s first break down how a 2-digit × 2-digit cryptarithm works.
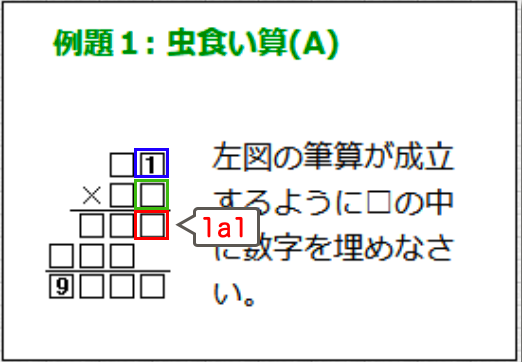
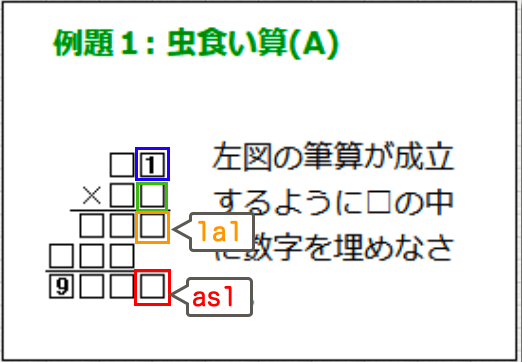
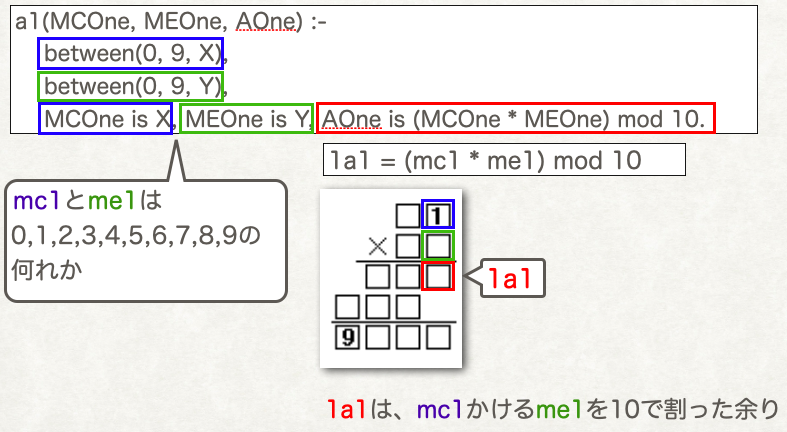
上図の赤枠の部分を「1a1」と名付けると、以下の様に説明できます。
If we label the red-framed part in the figure as 1a1, it can be described as follows:
→1a1は、青かける緑の、1の位の数
→1a1 represents the ones digit of blue multiplied by green.
です。と言うことは、
→1a1は、青かける緑を10で割った余り
→1a1 is the remainder when blue × green is divided by 10.
と言えます。
次の例として、
As the next example,
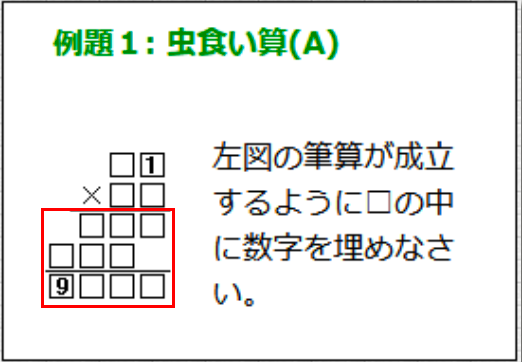
上図の赤枠の部分を「as1」と名付けると、以下の様に説明できます。
If we label the red-framed part in the figure as as1, it can be described as follows:
→as1は、1a1。
→as1 is 1a1.
次の例として、
As the next example,
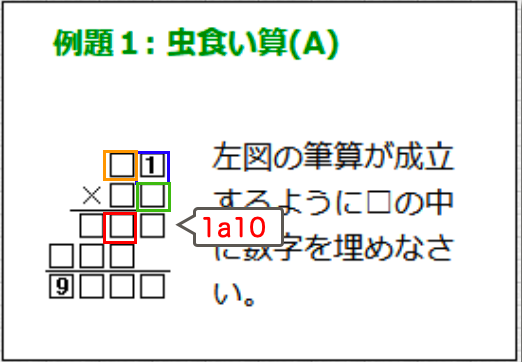
上図の赤枠の部分を「1a10」と名付けると、以下の様に説明できます。
If we label the red-framed part in the figure as 1a10, it can be described as follows:
→1a10は、青かける緑の10の位の数と、
黄かける緑の1の位の数を足した値の、
1の位の数
→1a10 represents the ones digit of the sum of:
the tens digit of blue × green, and
the ones digit of yellow × green.
以下同様にして、
Similarly,
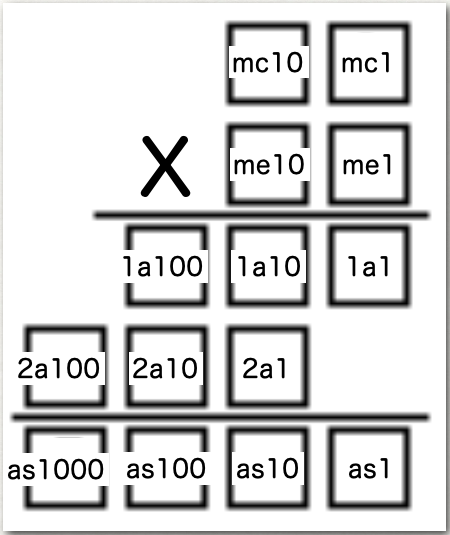
上図の赤枠部分を全て言葉で整理し、2桁かける2桁の虫食い算の各部に名前を付け、各部を表す式を書きました。
We organized all the red-framed parts in words, named each part of the 2-digit × 2-digit cryptarithm, and wrote expressions representing each part.
以下の式内の「mod」は「余りを求める」、「div」は「商を求める」という意味で使用しています。
In the formulas below, “mod” means “remainder” and “div” means “quotient”.
1a1 = (mc1 * me1) mod 10
1a10 = ((mc1 * me1) div 10 + (mc10 * me1) mod 10) mod 10
1a100 = ((mc1 * me1) div 10 + (mc10 * me1) mod 10) div 10 + (mc10 * me1) div 10
2a1 = (mc1 * me10) mod 10
2a10 = ((mc1 * me10) div 10 + (mc10 * me10) mod 10) mod 10
2a100 = ((mc1 * me10) div 10 + (mc10 * me10) mod 10) div 10 + (mc10 * me10) div 10
as1 = 1a1
as10 = (1a10 + 2a1) mod 10
as100 = ((1a10 + 2a1) div 10 + (1a100 + 2a10) mod 10 ) mod 10
as1000 = ((1a10 + 2a1) div 10 + (1a100 + 2a10) mod 10) div 10 + 2a100
この式をPrologの文法で書ければ実現できそうです!
If we can write these formulas in Prolog syntax, it should be possible to implement.
Prologの実装と実行結果 / Prolog Implementation and Results
ここでは、実際に2桁かける2桁の虫食い算をPrologで表現してみます。
Here, we’ll represent the 2-digit × 2-digit cryptarithm directly in Prolog.
- Prologによる2桁かける2桁の虫食い算 / 2-Digit × 2-Digit Cryptarithm in Prolog
a1(MCOne, MEOne, AOne) :-
% 一の位の計算
between(0, 9, X),
between(0, 9, Y),
MCOne is X, MEOne is Y, AOne is (MCOne * MEOne) mod 10.
a10(MCOne, MEOne, MCTen, ATen) :-
% 十の位の計算
between(0, 9, X),
between(0, 9, Y),
between(0, 9, Z),
MCOne is X, MEOne is Y, MCTen is Z, ATen is ((MCOne * MEOne) div 10 + (MCTen * MEOne) ) mod 10.
a100(MCOne, MEOne, MCTen, AHun) :-
% 百の位の計算
between(0, 9, X),
between(0, 9, Y),
between(0, 9, Z),
MCOne is X, MEOne is Y, MCTen is Z, AHun is ((MCOne * MEOne) div 10 + (MCTen * MEOne) mod 10) div 10 + (MCTen * MEOne) // 10.
as1(MCOne, MEOne, OneAOne, ASOne) :-
% 答えの一の位
a1(MCOne, MEOne, OneAOne),
ASOne is OneAOne.
as10(MCOne, MEOne, MCTen, METen, OneATen, TwoAOne, ASTen) :-
% 答えの十の位
a10(MCOne, MEOne, MCTen, OneATen),
a1(MCOne, METen, TwoAOne),
ASTen is (OneATen + TwoAOne) mod 10.
as100(MCOne, MEOne, MCTen, METen, OneATen, OneAHun, TwoAOne, TwoATen, ASHun) :-
% 答えの百の位
a10(MCOne, MEOne, MCTen, OneATen),
a1(MCOne, METen, TwoAOne),
a100(MCOne, MEOne, MCTen, OneAHun),
a10(MCOne, METen, MCTen, TwoATen),
ASHun is ((OneATen + TwoAOne) div 10 + (OneAHun + TwoATen) mod 10) mod 10.
as1000(MCOne, MEOne, MCTen, METen, OneATen, OneAHun, TwoAOne, TwoATen, TwoAHun, ASTho) :-
% 答えの千の位
a10(MCOne, MEOne, MCTen, OneATen),
a1(MCOne, METen, TwoAOne),
a100(MCOne, MEOne, MCTen, OneAHun),
a10(MCOne, METen, MCTen, TwoATen),
a100(MCOne, METen, MCTen, TwoAHun),
ASTho is ((OneATen + TwoAOne) div 10 + (OneAHun + TwoATen) ) div 10 + TwoAHun.
mushikui(MCOne, MEOne, MCTen, METen, OneAOne, OneATen, OneAHun, TwoAOne, TwoATen, TwoAHun, ASOne, ASTen, ASHun, ASTho) :-
% 虫食い算(上記全てのルールを満たす)
as1(MCOne, MEOne, OneAOne, ASOne),
as10(MCOne, MEOne, MCTen, METen, OneATen, TwoAOne, ASTen),
as100(MCOne, MEOne, MCTen, METen, OneATen, OneAHun, TwoAOne, TwoATen, ASHun),
as1000(MCOne, MEOne, MCTen, METen, OneATen, OneAHun, TwoAOne, TwoATen, TwoAHun, ASTho).
Prologのルール「a1」について以下の図で説明します。
The figure below illustrates how the Prolog rule a1 works.
以降、同様に2桁かける2桁の虫食い算の各部の式をPrologの文法に沿って直していきました。
From here, each part of the 2-digit × 2-digit cryptarithm was converted into Prolog syntax.
Prologのコーディング中に、ルール「1a1」と「2a1」は全く同じであることに気づき、共通ルール「a1」としました。
While coding, I noticed that the rules “1a1” and “2a1” are identical, so I created a common rule “a1”.
その他も共通化できるところはしてあります。
Other parts were also unified wherever possible.
Prologの、2桁かける2桁の虫食い算プログラムはこれで全部です。
This completes the Prolog program for the 2-digit × 2-digit cryptarithm.
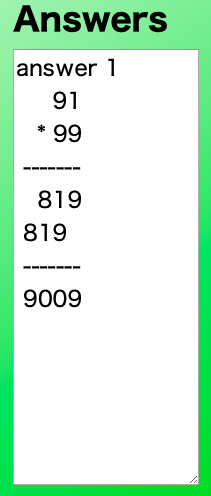
試しに例題「mc1が1、as1000が9になる2桁かける2桁のかけ算は?」を実行してみます。
As a test, let’s execute the query: “Find the 2-digit × 2-digit multiplication where mc1 = 1 and as1000 = 9.”
?- mushikui(1, MEOne, MCTen, METen, OneAOne, OneATen, OneAHun, TwoAOne, TwoATen, TwoAHun, ASOne, ASTen, ASHun, 9).
MEOne = MCTen, MCTen = METen, METen = OneAOne, OneAOne = TwoAOne, TwoAOne = ASOne, ASOne = 9,
OneATen = TwoATen, TwoATen = 1,
OneAHun = TwoAHun, TwoAHun = 8,
ASTen = ASHun, ASHun = 0 ;
false.
正しい答えが出ているのですが、出力だけでは少し分かりづらいので、Prologが出力した答えを以下の図に記載します。
Here’s a visualization of the output generated by Prolog.
Prolog、やっぱり面白いですよね! 本当にPrologの力を実感しました。
Prolog really is fascinating, isn’t it?
同書籍から文を少し変えて引用させてもらいます。(変えた部分は赤文字にしています。)
I have slightly modified the text from the book for quoting here (modified parts are in red).
2桁かける2桁の虫食い算を解く方法が見つかった。
わずか50行のコードで答えが見つかった。プログラムはどこに?
なんと、アルゴリズムなんか気にしなくて良いのだ。
上の問題をお好みの手続き型言語で解いてみてほしい。
解法はわかりやすいだろうか?このような複雑なロジックを含む問題をRustやGoで解くための手順を考えてみるとよい。
Tauriで「2桁かける2桁の虫食い算」GUIを作成 / Creating a 2-Digit × 2-Digit Cryptarithm GUI with Tauri
Prologを実際の問題解決に使って感じた「Prologすげーっ!これだけでできんの!?」という感動を皆様と共有したいとき、足りないのがパッと見のわかりやすさだと感じました。
When I wanted to share the excitement of “Wow, Prolog is amazing! It can do this all by itself!?” from actually solving problems with Prolog, I felt that what was missing was immediate visual clarity.
そこで本記事の最後として、私が大好きな言語の一つであるRustのGUIフレームワークTauriを使って作成した「2桁かける2桁の虫食い算GUI」を紹介します。
So, as the final part of this article, I’d like to introduce the “2-Digit × 2-Digit Cryptarithm GUI” I created using Tauri
, a GUI framework for Rust, one of my favorite programming languages.
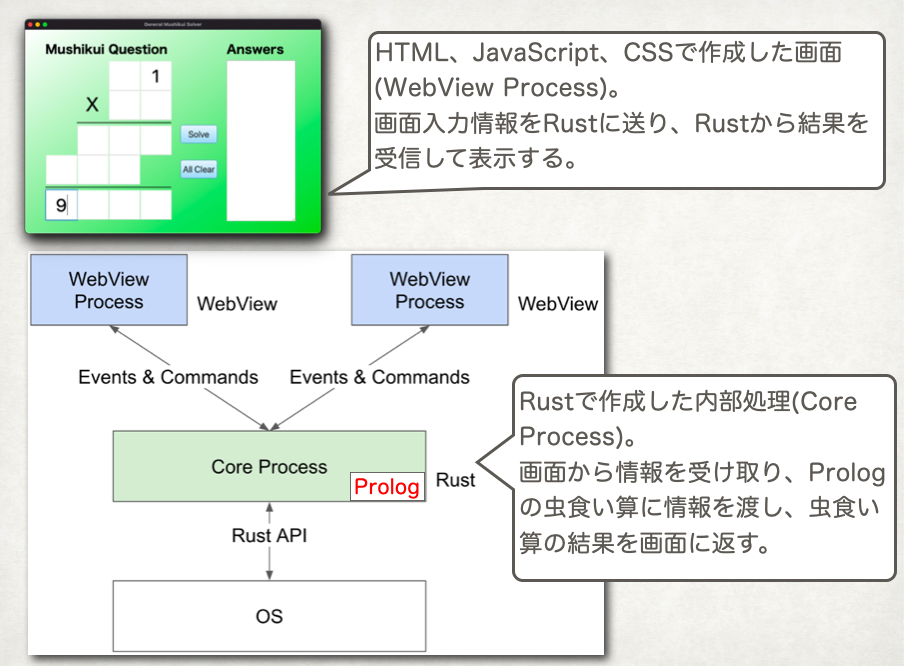
概略構成図を以下に記載します。
Below is a schematic overview of its structure.
上図左下の「WebView Process」などが書かれた部分はRust GUI の決定版! Tauri を使ってクロスプラットフォームなデスクトップアプリを作ろうから引用させてもらいました。
今回は画面(WebView Process)をClojureScriptで作成しました。
The frontend is written in ClojureScript.
RustのプログラムからPrologの虫食い算を呼ぶところにはRustのクレートswipl-rsを使用しました。(こんな素晴らしいクレートがあるなんて!作者の方、ありがとうございます!)
To call the Prolog cryptarithm from the Rust program, I used the Rust crate swipl-rs
. (I can’t believe such a wonderful crate exists! Thank you to the author!)
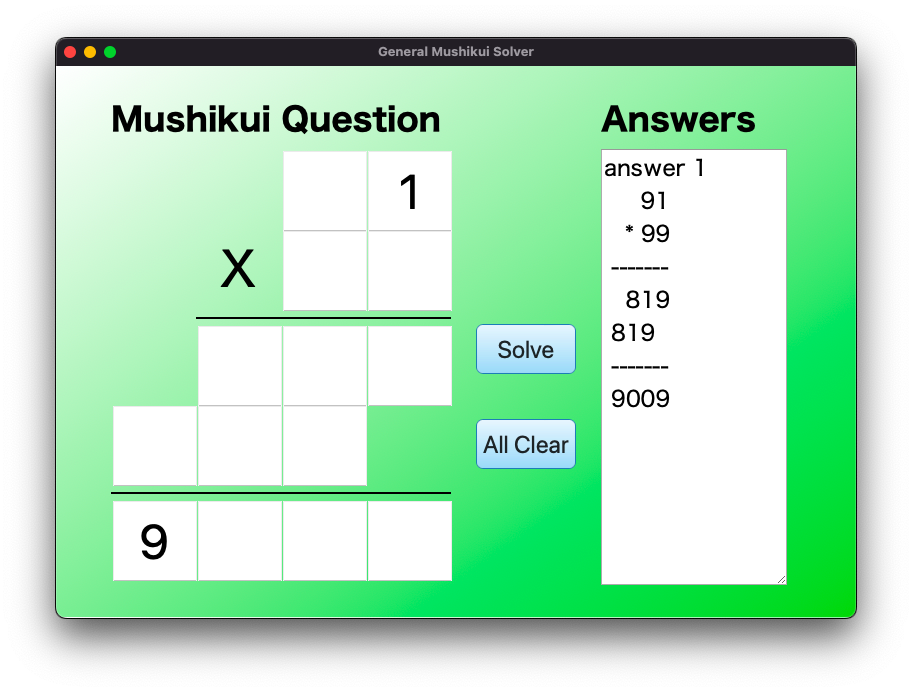
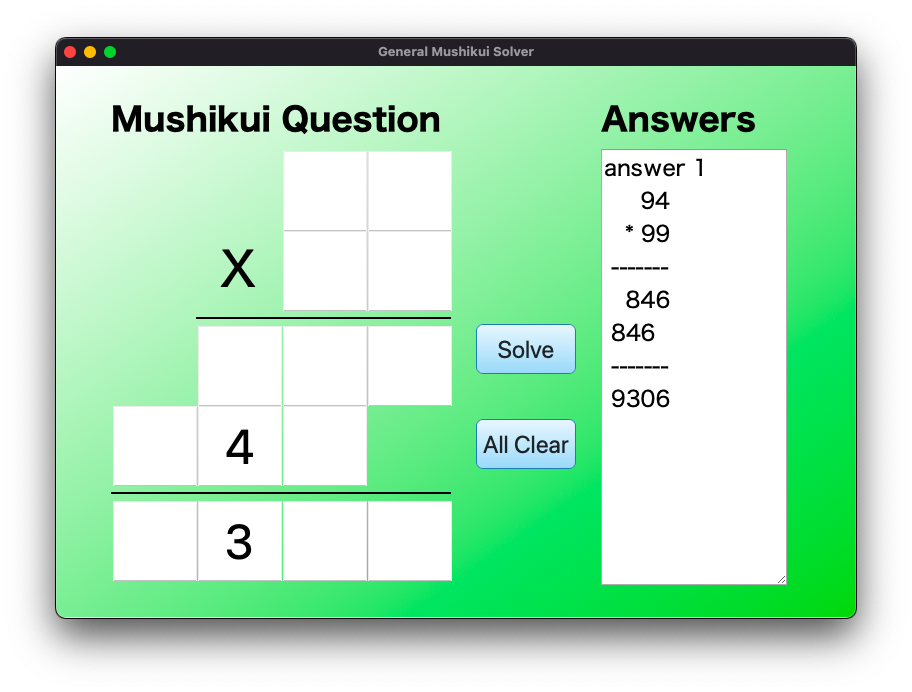
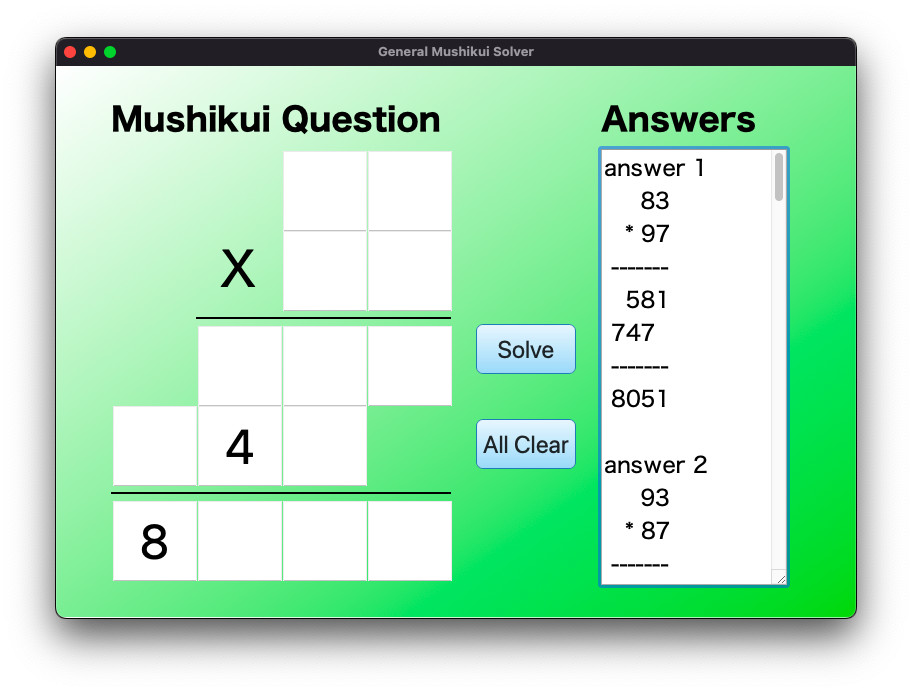
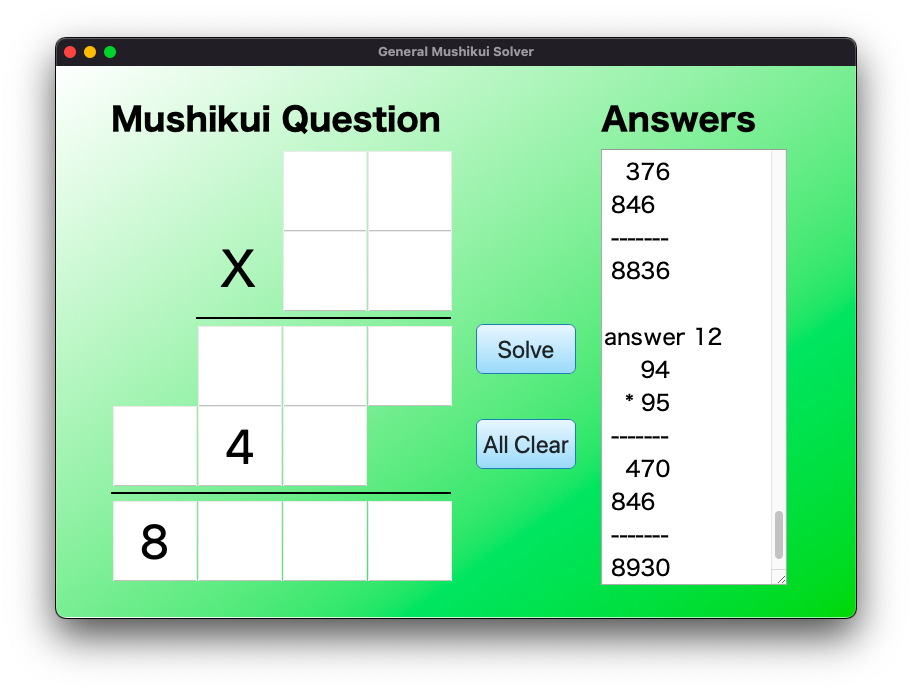
以下の図に、虫食い算GUIの実行結果例をいくつか記載します。
Below are some examples of the cryptarithm GUI execution results.
答えが無いときは無い(No answers)と表示します。
If there is no solution, it displays “No answers”.
答えが複数あるときは全部表示します。
If there are multiple solutions, all of them are displayed.
Tauriの2桁かける2桁の虫食い算プロジェクト全体は以下のGutHubにあります。
The entire Tauri 2-digit × 2-digit cryptarithm project is available on GitHub below.
mushikui-tauri
まとめ / Conclusion
Prologは、得意分野の問題においては、他の言語を寄せ付けない圧倒的な力を発揮します。
Prolog demonstrates overwhelming power in its areas of expertise, outperforming other languages with ease.
もし論理パズルや探索問題に興味があるなら、ぜひPrologを触ってみてください!
If you’re interested in logic puzzles or search problems, I highly recommend giving Prolog a try!
他にもPrologを適用したら面白そうな題材があればコメントで教えてもらえるとありがたいです!
If you know other types of problems where applying Prolog could be interesting, I’d love for you to share them in the comments!