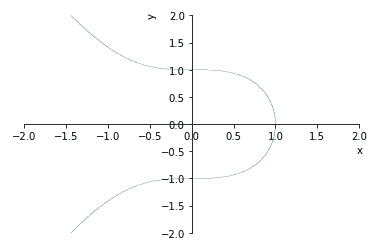可視化は大事
結果が関数で求まってもどういうものかは直感的にわからないことが多い。
そこでグラフを描くことが分析・思考のための第一歩になる。
matplotlibの日本語メモはここが詳しい。
sympyのplotはここ。
公式とかも見ながら四苦八苦。
import
import sympy as sym
sym.init_printing()
Pi = sym.S.Pi # 円周率
E = sym.S.Exp1 # 自然対数の底
I = sym.S.ImaginaryUnit # 虚数単位
# 使用する変数の定義(小文字1文字は全てシンボルとする)
(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z) = sym.symbols('a b c d e f g h i j k l m n o p q r s t u v w x y z')
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
色を頑張る
色のリストはLab色空間で輝度一定の環になるように、別プログラムで事前生成した。
色の鮮やかさよりコントラストに安全マージンを持たせた設計で、色弱は未考慮。
各リストは37個のHEX文字列からなる。
37という数字は1周の360度を10度ずつ進む数である36に最も近い素数ということで選択した。
(37だと1当たり9.73度進む。)
素数だから初期色とステップ数をどのように選んでも(原始根でないとダメです)37色を必ず1色ずつ通る巡回群となる。
これにより約ステップ数10度ほど位相が進むという直感上の一致と、
できる限り同じ色が出ずに長周期になることを両立させた。
def generator_p(start): # 引数が指定されればその色をそうでないときは順番に色を生成するためのジェネレーター
prime = 37 # リストの数 (素数なのでprimitiveに何を指定しても必ず最大周期になる)
primitive = 8 # 生成元 (1ステップ当たり色相がprimitive * 37/360度進む)
g0 = start # 開始元 (実際に返されるのは g0 * primitive)
while True:
val = yield g0
if val: # ジェネレーターに引数が渡されるとそれを開始元としてリセットする
g0 = val
g0 += primitive
if g0 >= prime: # 剰余を取る
g0 -= prime
gen_hexnum = generator_p(0) # 引数に初期色を入れる
gen_hexnum.__next__() # ジェネレーターの初期化
def hexNum(num, type): # 色のリスト
# 基本色(白背景で汎用的に使える落ち着いた色)
color_basic = ['#9c1954', '#9e1a46', '#9d1e38', '#9a252a', '#962d1c', '#8f350d', '#873c00',
'#7d4300', '#734900', '#674f00', '#5b5300', '#4d5700', '#3e5b00', '#2b5d00',
'#0f6009', '#00611c', '#00632b', '#00643a', '#006449', '#006558', '#006567',
'#006575', '#006482', '#00648e', '#006298', '#0060a0', '#005ea6', '#005baa',
'#0056aa', '#0051a9', '#2f4ca4', '#50459d', '#673d94', '#78358a', '#862d7d', '#902470', '#981e62']
# 彩度の高い色(目立つが多用はしないほうがよい。)
color_vivid = ['#ffadc7', '#ffadbc', '#ffaeb2', '#ffb0a8', '#ffb29e', '#ffb596', '#f9b88f',
'#f1bc8a', '#e9bf86', '#dfc385', '#d5c685', '#caca87', '#becd8b', '#b2cf90',
'#a6d298', '#99d4a0', '#8dd5aa', '#80d7b4', '#74d7bf', '#6ad8ca', '#61d8d5',
'#5bd7e0', '#59d6e9', '#5dd5f2', '#65d3f9', '#71d1ff', '#7fceff', '#8ecbff',
'#9ec8ff', '#afc4ff', '#bec1ff', '#cdbdfd', '#dab9f7', '#e6b6ef', '#f0b3e6', '#f9b0dc', '#ffaed2']
# 薄い色(白背景では使わない。黒背景で使うことを想定。)
color_thin = ['#ffc3d5', '#ffc3cd', '#ffc3c5', '#ffc4be', '#ffc6b7', '#ffc8b1', '#fbcaac',
'#f5cca9', '#efcfa6', '#e8d2a5', '#e0d4a5', '#d8d7a6', '#cfd9a9', '#c6dbad',
'#bdddb3', '#b5deb9', '#ace0c0', '#a5e0c7', '#9ee1cf', '#98e1d7', '#94e1df',
'#92e1e6', '#92e0ed', '#94dff4', '#99def9', '#9fdcfd', '#a7daff', '#b1d8ff',
'#bbd5ff', '#c5d3ff', '#cfd0ff', '#dacdfc', '#e3cbf7', '#ecc8f2', '#f3c6eb', '#f9c5e4', '#fec4dc']
if (type == 'thin'):
hex_list = color_thin
elif (type == 'vivid'):
hex_list = color_vivid
else:
hex_list = color_basic
if num is not None:
gen_hexnum.send(num)
return hex_list[gen_hexnum.__next__()]
2次元グラフplot関数の作成:1変数陽関数
def plot(func, xrange, ylim=None, xlog=None, ylog=None, cn=None, ct='basic', close=None, figs=None, simbol=x):
if figs:
plt.figure(figsize=figs)
X = np.arange(xrange[0], xrange[1], xrange[2])
if hasattr(func, "subs"): # sympy
Y = [func.subs([(simbol, K)]) for K in X]
else: # scipy
Y = [func(K) for K in X]
if ylim:
plt.ylim(ylim)
if xlog:
plt.xscale('log')
else:
plt.xscale('linear')
if ylog:
plt.yscale('log')
else:
plt.yscale('linear')
plt.plot(X, Y, color=hexNum(cn, ct))
if close:
plt.show()
plt.close()
素のmatplotlib.plotはややこしいのでよく使う引数だけをラップした関数を作った。
関数と幅、色程度を与えたら後はよしなにしてくれというぐらいの方が使いやすい。
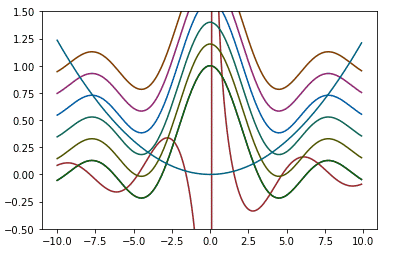
F = sym.sin(x)/x
G = sym.cos(x)/x
plot(F, (-10, 10, 0.1), cn=0, figs=(10, 6))
plot(G, (-10, 10, 0.1))
plot(F+0.2, (-10, 10, 0.1))
plot(F+0.4, (-10, 10, 0.1))
plot(F+0.6, (-10, 10, 0.1))
plot(F+0.8, (-10, 10, 0.1))
plot(F+1.0, (-10, 10, 0.1))
def A(x):
return np.sin(x)/x
plot(A, (-10, 10, 0.1))
plot(lambda X: (X/9.0)**2, (-10, 10, 0.1), (-0.5, 1.5), close=True)
sympyを快適に使うには小文字は全てシンボルにしたいので、
関数名やループ変数は意識的に大文字にするようにしている。
colorによる色分け効果、hasattrによるsympyとnumpy関数の自動判定、
close引数でオプションはまとめて最後だけに書けば良くなった。
かなり直感的にプロットができるようになったので満足のいく出来。
ただグラフを見ると$\frac{\cos(x)}{x}$の極が変。
$-\infty\longrightarrow\infty$の途中の線が描写されている雰囲気だが
解決策あるのかな。
2次元グラフplot関数の作成:媒介変数表示
def plotp(func, t_range=(-4, 4, 100), axis=[-4, 4, -4, 4],
xlog=None, ylog=None, cn=None, ct='basic', close=None, figs=None, simbol=t):
if figs:
plt.figure(figsize=figs)
X, Y = func
t_ndarray = np.linspace(t_range[0], t_range[1], t_range[2]) # ndarray
if hasattr(X, "subs"): # sympy
Xp = np.array([float(sym.N(X.subs([(simbol, T)]))) for T in t_ndarray])
Yp = np.array([float(sym.N(Y.subs([(simbol, T)]))) for T in t_ndarray])
else: # scipy
Xp = [X(K) for K in t_ndarray]
Yp = [Y(K) for K in t_ndarray]
plt.axis(axis)
if xlog:
plt.xscale('log')
else:
plt.xscale('linear')
if ylog:
plt.yscale('log')
else:
plt.yscale('linear')
plt.plot(Xp, Yp, color=hexNum(cn, ct))
if close:
plt.show()
plt.close()
plot()との違いはFuncが2関数のリストで渡され、x, yの領域を指定するaxisが加わっている。
シンボルは慣例からtをデフォルトとした。
またtのレンジの3つ目として刻み幅ではなく分割数で指定するようにしている。
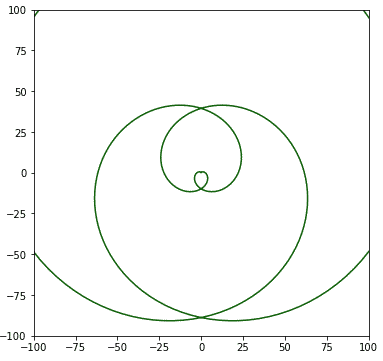
X = t**2 * sym.sin(t)
Y = t**2 * sym.cos(t)
plotp([X, Y], (-4 * np.pi, 4 * np.pi, 400), [-100, 100, -100, 100], figs=(6, 6), close=True)
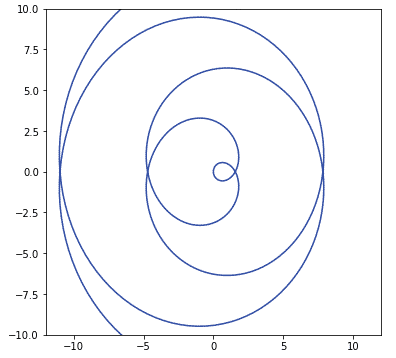
plotp([lambda T: T * np.sin(T), lambda T: T * np.cos(T)], (-4 * np.pi, 4 * np.pi, 400), [-12, 12, -10, 10],
cn=14, figs=(6, 6), close=True)
sympy, scipyの両方でうまくいった。
2次元グラフplot関数の作成:2変数陰関数
$F(x, y)=0$の形式で表現される関数である。
陰関数を直接扱うのは難しそう。
なのでsympyのplot_implicitをそのまま使う。
F = x**3 + y**2 -1
sym.plot_implicit(F, (x, -2, 2), (y, -2, 2), line_color=hexNum(2, 'basic'))
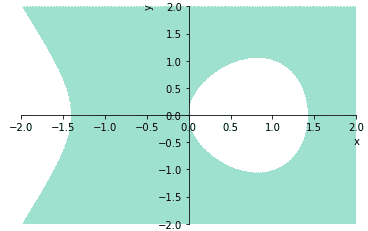
F = x**3 - 2 * x + y**2 > 0
sym.plot_implicit(F, (x, -2, 2), (y, -2, 2), line_color=hexNum(2, 'thin'))
不等式が使えるのが利点。
3次元グラフplot関数の作成:2変数陽関数
$z=f(x, y)$の形の関数である。
from matplotlib import cm
def plot3D(func, xrange=(-2, 2, 0.1), yrange=(-2, 2, 0.1), ptype='plot', simbol=[x, y]):
fig = plt.figure()
ax = Axes3D(fig)
if ptype == 'plot':
ax.plot(func[0], func[1], func[2])
plt.show()
plt.close()
return
X = np.arange(xrange[0], xrange[1], xrange[2])
Y = np.arange(yrange[0], yrange[1], yrange[2])
Xmesh, Ymesh = np.meshgrid(X, Y)
if hasattr(func, "subs"): # sympy
Z = np.array([np.array([float(sym.N(func.subs([(simbol[0], K), (simbol[1], L)]))) for K in X]) for L in Y])
else: # scipy
Z = func(Xmesh, Ymesh)
if ptype == 'surface':
ax.plot_surface(Xmesh, Ymesh, Z, cmap=cm.bwr)
elif ptype == 'wireframe':
ax.plot_wireframe(Xmesh,Ymesh, Z)
elif ptype == 'contour':
ax.contour3D(X, Y, Z)
plt.show()
plt.close()
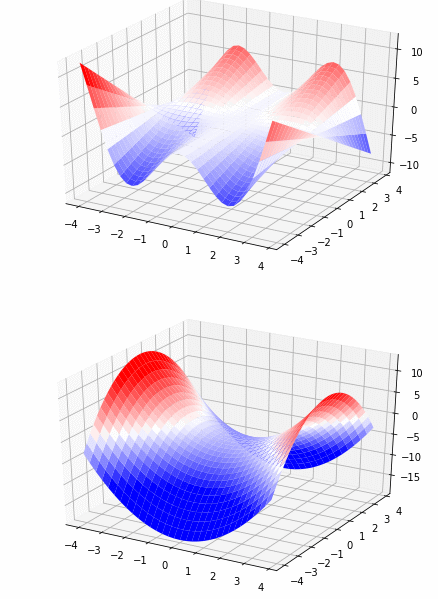
plot3D(lambda T, U: T * U * np.sin(T), (-4, 4, 0.25), (-4, 4, 0.25), 'surface')
plot3D((x ** 2 - 3 - y ** 2), (-4, 4, 0.25), (-4, 4, 0.25), 'surface')
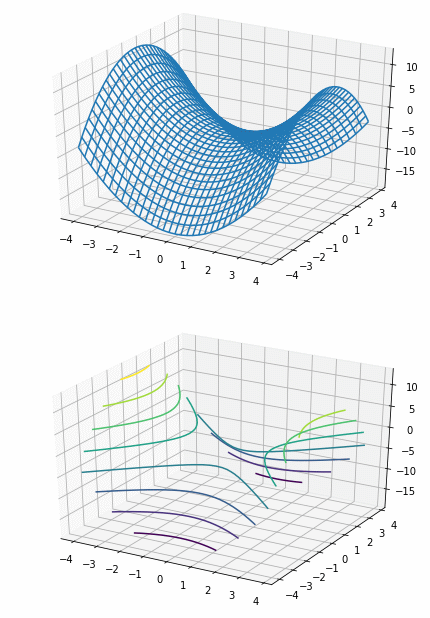
plot3D((x ** 2 - 3 - y ** 2), (-4, 4, 0.25), (-4, 4, 0.25), 'wireframe')
plot3D((x ** 2 - 3 - y ** 2), (-4, 4, 0.25), (-4, 4, 0.25), 'contour')
3次元は輝度差を出して浮き沈みを見た方が良いからデフォルトのカラーを採用。
曲率が負の宇宙の図でよく出てくる馬の鞍の関数をプロットしてみた。
3次元グラフplot関数の作成:媒介変数表示
def plotp3(func, simbol=[t], rangeL=[(-4, 4, 100)]):
X, Y, Z = func
t1 = simbol[0]
if len(simbol) >= 2:
u1 = simbol[1]
t_rangeL = rangeL[0]
t_ndarray = np.linspace(t_rangeL[0], t_rangeL[1], t_rangeL[2]) # ndarray
if len(rangeL) >= 2:
u_rangeL = rangeL[1]
u_ndarray = np.linspace(u_rangeL[0], u_rangeL[1], u_rangeL[2]) # ndarray
if len(rangeL) == 1:
Xp = np.array([float(sym.N(X.subs([(t1, T)]))) for T in t_ndarray])
Yp = np.array([float(sym.N(Y.subs([(t1, T)]))) for T in t_ndarray])
Zp = np.array([float(sym.N(Z.subs([(t1, T)]))) for T in t_ndarray])
else:
Xp = np.array([float(sym.N(X.subs([(t1, T), (u1, U)]))) for T in t_ndarray for U in u_ndarray])
Yp = np.array([float(sym.N(Y.subs([(t1, T), (u1, U)]))) for T in t_ndarray for U in u_ndarray])
Zp = np.array([float(sym.N(Z.subs([(t1, T), (u1, U)]))) for T in t_ndarray for U in u_ndarray])
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(Xp, Yp, Zp)
plt.show()
plt.close()
X = 2*sym.cos(t)
Y = 5*sym.sin(t)
Z = t
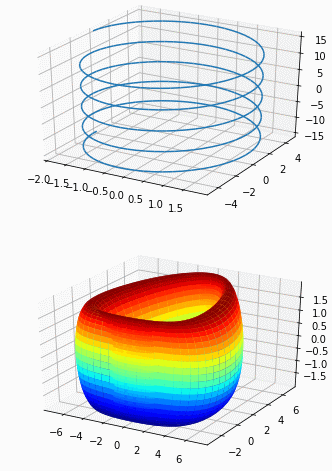
plotp3([X, Y, Z], [t], [(-5 * np.pi, 5 * np.pi, 200)])
X = (5+2*sym.cos(t))*sym.cos(u)
Y = (5+2*sym.sin(u))*sym.sin(u)
Z = 2*sym.sin(t)-u/sym.oo
plotp3([X, Y, Z], [t, u], [(-np.pi, np.pi, 40), (-np.pi, np.pi, 40)])
この辺から疲れてきた。
3次元はsympyデフォルトのでいいよ。
X = 2*sym.cos(t)
Y = 5*sym.sin(t)
Z = t
sym.plotting.plot3d_parametric_line(X, Y, Z, (t, -5*np.pi, 5*np.pi))
X = (5+2*sym.cos(t))*sym.cos(u)
Y = (5+2*sym.sin(u))*sym.sin(u)
Z = 2*sym.sin(t)-u/sym.oo
sym.plotting.plot3d_parametric_surface(X, Y, Z, (t, -np.pi, np.pi), (u, -np.pi, np.pi))