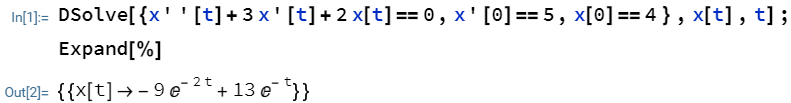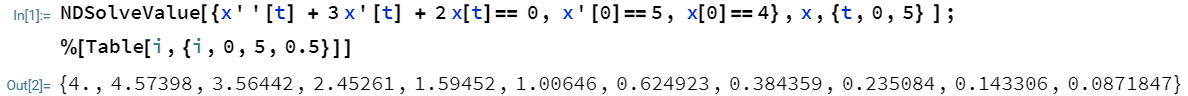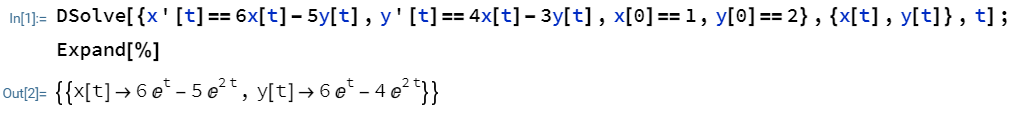More than 1 year has passed since last update.

LabVIEW / 常微分方程式を解くための各種VIの使いかた

LabVIEW

Last updated at 2023-01-09Posted at 2019-03-17

概要

LabVIEWには、常微分方程式を解くためのVIがいくつか最初から用意されているが、サンプルVIがなかったり、あってもやたら複雑だったりするので、ここではごく単純な常微分方程式をただ単に解くだけのサンプルVIを示す。LabVIEWはHome Bundle版を使った。

下の9つのVIがある。
　　1. ODEシンボリック線形n次~~システム~~ VI (n階線形ODEの記号解)
　　2. ODE数値線形n次~~システム~~ VI 　　　　(n階線形ODEの数値解)
　　3. ODEシンボリック線形システム VI　　(連立線形ODEの記号解)
　　4. ODE数値線形システム VI　　　　　　(連立線形ODEの数値解)
　　5. ODEオイラー法 VI
　　6. ODE4次ルンゲ・クッタ法 VI
　　7. ODE5次キャッシュ・カープ法 VI (フェールベルク法の改良版)
　　8. ODEソルバー VI (解法が切り換えられる)
　　　　　　0 Runge-Kutta 1 (Euler)
　　　　　　1 Runge-Kutta 2
　　　　　　2 Runge-Kutta 3
　　　　　　3 Runge-Kutta 4
　　　　　　4 Runge-Kutta 23 (variable)
　　　　　　5 Runge-Kutta 45 (variable)
　　　　　　6 BDF (variable)
　　　　　　7 Adams-Moulton (variable)
　　　　　　8 Rosenbrock (variable)
　　　　　　9 Discrete States Only
　　9. DAE 5次Radau法 VI (微分代数方程式の解法)

1. ODEシンボリック線形n次システム VI (n階線形ODEの記号解)

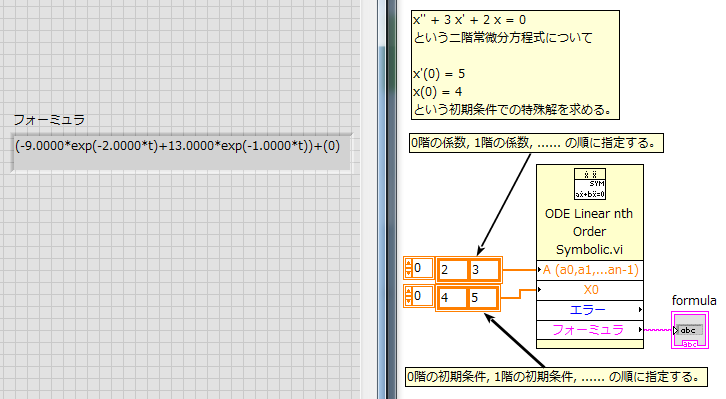
VIファイル名:「ODE Linear nth Order Symbolic.vi」

和名に「システム」とあるが英名に「system」(「連立」の意) は含まれていない。「order」は「階数」、「symbolic」は「記号解(厳密解、解析解)」。

1.1 この常微分方程式を解く

x'' + 3 x' + 2 x = 0
という二階常微分方程式について

x'(0) = 5
x(0) = 4
という初期条件での特殊解を求める。

1.2 サンプルVI

https://drive.google.com/open?id=1_pymSz0hLm63eKqRmHo8Z8SRG6_4s_4i
各階の係数と初期条件とを指定する順番に注意する。[エラー]はVIの実行エラー。独立変数には"t"が使われる。

1.3 Wolframによる検算

DSolve[{x''[t]+3 x'[t]+2 x[t]==0,x'[0]==5,x[0]==4 },x[t],t];
Expand[%]

2. ODE数値線形n次システム VI (n階線形ODEの数値解)

VIファイル名:「ODE Linear nth Order Numeric.vi」

和名に「システム」とあるが英名に「system」(「連立」の意) は含まれていない。「order」は「階数」、「numeric」は「数値解(近似解)」。

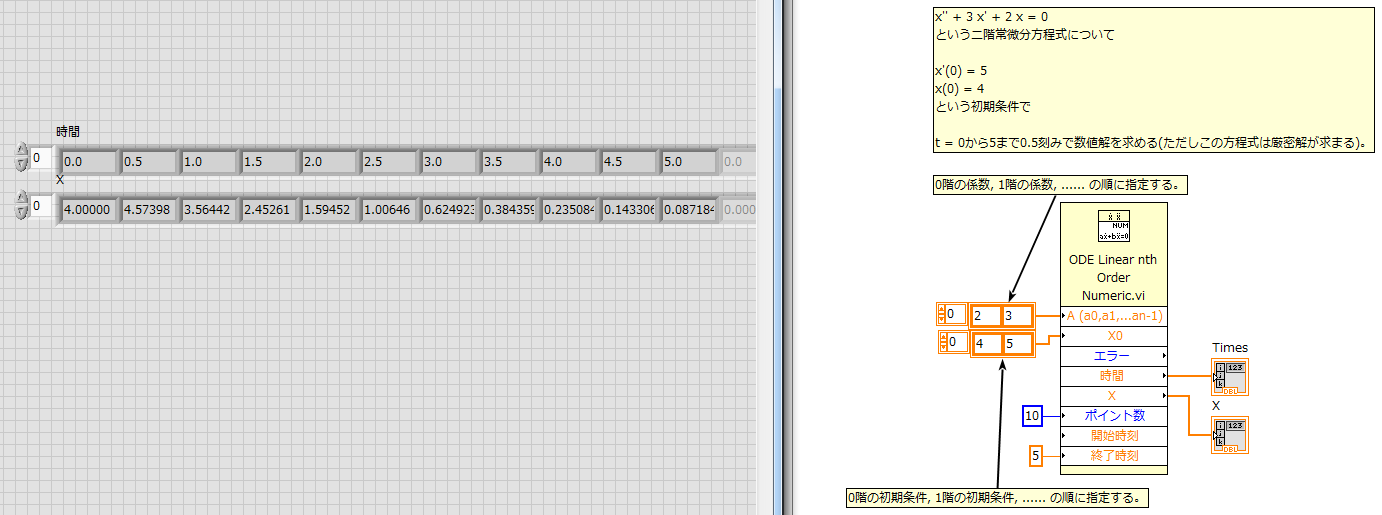
2.1 この常微分方程式を解く

x'' + 3 x' + 2 x = 0
という二階常微分方程式について

x'(0) = 5
x(0) = 4
という初期条件で

t = 0から5まで0.5刻みで数値解を求める(ただしこの方程式は厳密解が求まる)。

2.2 サンプルVI

https://drive.google.com/open?id=1ljuo2WlwJ3mTJtVYCXCILc0DUeorylbe
各階の係数と初期条件とを指定する順番に注意する。[エラー]はVIの実行エラー。[開始時刻]はデフォルト(0)をそのまま使うので配線していない。[時間]は要するに独立変数のこと。

2.3 Wolframによる検算

NDSolveValue[{x''[t] + 3 x'[t] + 2 x[t]== 0, x'[0]==5, x[0]==4},x,{t,0,5} ];
%[Table[i,{i,0,5,0.5}]]

3. ODEシンボリック線形システム VI (連立線形ODEの記号解)

VIファイル名:「ODE Linear System Symbolic.vi」

systemは「連立」、symbolicは「記号解(厳密解、解析解)」。

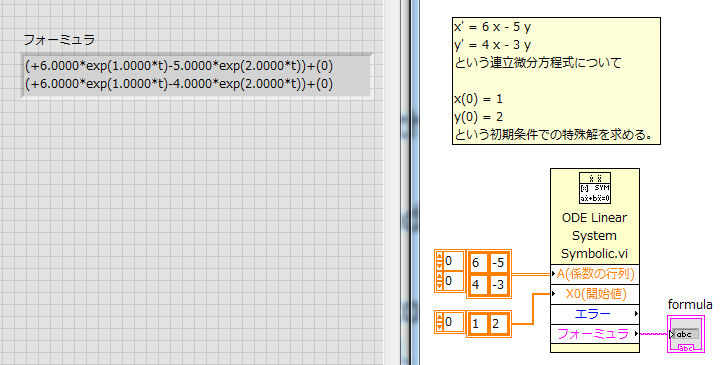
3.1 この常微分方程式を解く

x' = 6 x - 5 y
y' = 4 x - 3 y
という連立微分方程式について

x(0) = 1
y(0) = 2
という初期条件での特殊解を求める。

3.2 サンプルVI

https://drive.google.com/open?id=1H3T2y2f_YbcatUnkIDh2NXIpc0Tpln8A
[エラー]はVIの実行エラー。独立変数には"t"が使われる。

3.3 Wolframによる検算

DSolve[{x'[t]==6x[t]-5y[t],y'[t]==4x[t]-3y[t],x[0]==1,y[0]==2},{x[t],y[t]},t]

4. ODE数値線形システム VI (連立線形ODEの数値解)

VIファイル名:「ODE Linear System Numeric.vi」

systemは「連立」、numericは「数値解(近似解)」。

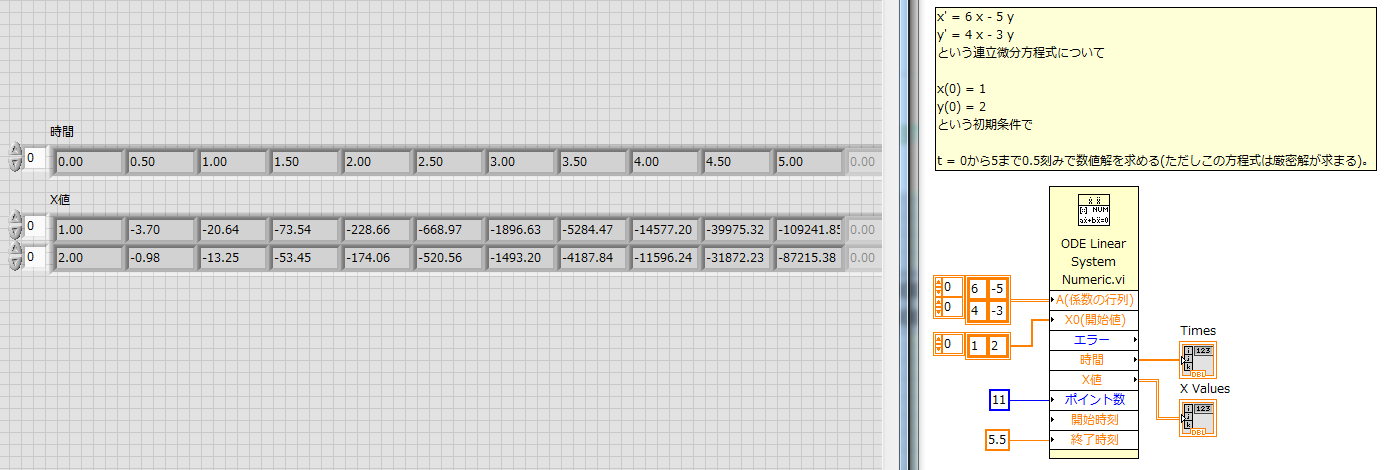
4.1 この常微分方程式を解く

x' = 6 x - 5 y
y' = 4 x - 3 y
という連立微分方程式について

x(0) = 1
y(0) = 2
という初期条件で

t = 0から5まで0.5刻みで数値解を求める(ただしこの方程式は厳密解が求まる)。

4.2 サンプルVI

https://drive.google.com/open?id=1ig3z6tycMIN9lCA-q8atvZ8qA8fmegSF
[ポイント数]、[終了時刻]の挙動が「ODE Linear nth Order Numeric.vi」と違う。[エラー]はVIの実行エラー。[開始時刻]はデフォルト(0)をそのまま使うので配線していない。[X値]配列の[0]行目がxの解、[1]行目がyの解。[時間]は要するに独立変数のこと。

4.3 Wolframによる検算

sol=NDSolveValue[{x'[t]==6x[t]-5y[t],y'[t]==4x[t]-3y[t],x[0]==1,y[0]==2},{x,y},{t,0,5}];
sol[[1]][Table[i,{i,0,5,0.5}]]
sol[[2]][Table[i,{i,0,5,0.5}]]

5. ODEオイラー法、
6. ODE4次ルンゲ・クッタ法、
7. ODE5次キャッシュ・カープ法

VIファイル名:
「ODE Euler Method.vi」
「ODE Runge Kutta 4th Order.vi」
「ODE Cash Karp 5th Order.vi」(フェールベルク法の改良版)

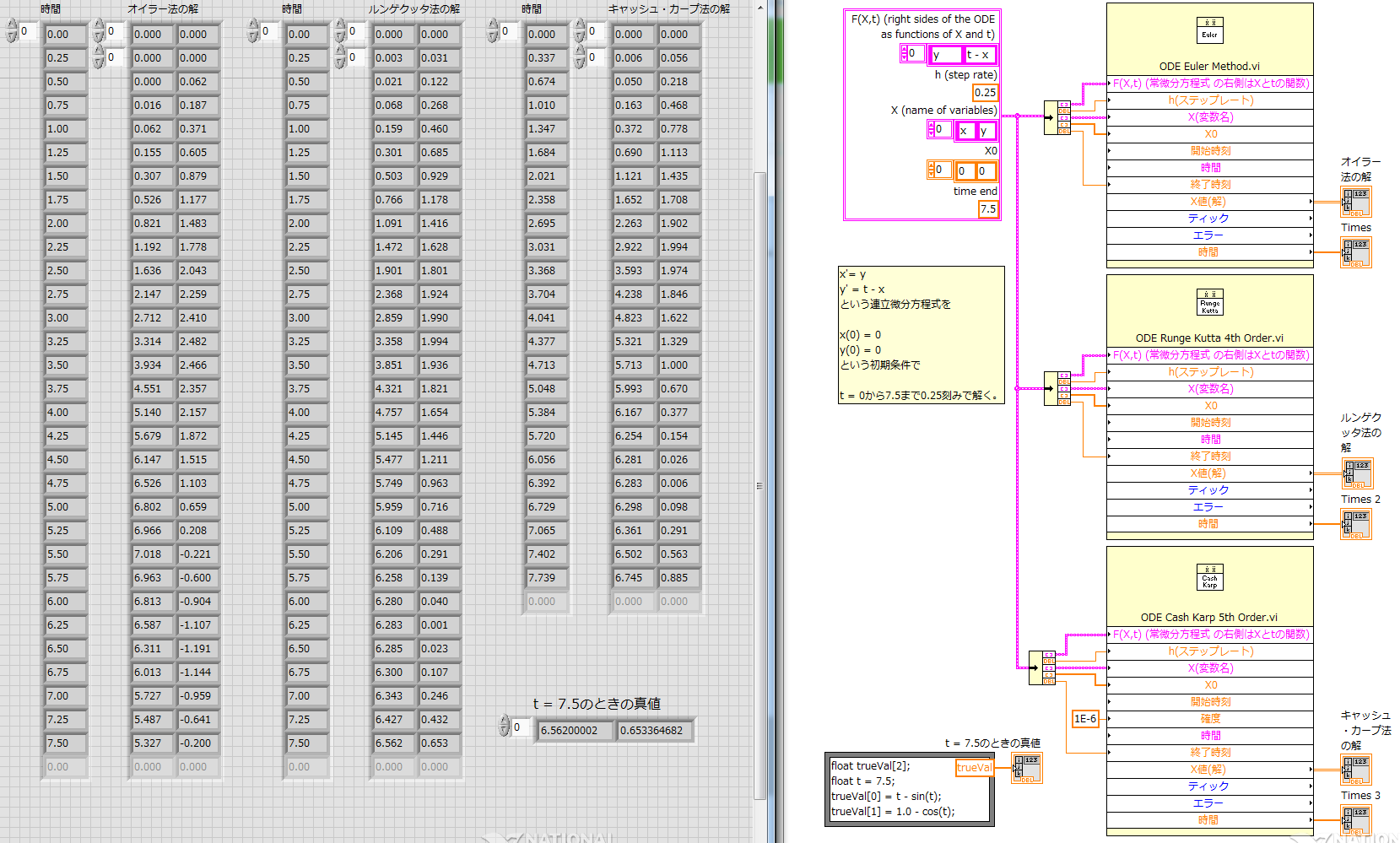
5.1、6.1、7.1 この常微分方程式を解く

x' = y
y' = t - x
という連立微分方程式を

x(0) = 0
y(0) = 0
という初期条件で

t = 0から7.5まで0.25刻みで解く。

5.2、6.2、7.2 サンプルVI

https://drive.google.com/open?id=1fRYLByS4lLw1U8A_a-UevOGwHDI1_qws
「ODE Euler Method.vi」「ODE Runge Kutta 4th Order.vi」「ODE Cash Karp 5th Order.vi」はどれも使いかたが同じなので、比較できるよう1つのサンプルVIにまとめた。

[開始時刻]はデフォルト(0)をそのまま使うので配線していない。
[時間]は独立変数文字列。デフォルト("t")をそのまま使うので配線していない。
[ティック]は計算に要したミリ秒数。
[エラー]はVIの実行エラー。
[F(X,t) (常微分方程式の右側はXとtの関数)]とあるのは[F(X,t) (常微分方程式X'=F(X,t)の右辺)]のこと。

以下の例ではそれぞれ[0]列目がxの解、[1]列目がyの解。「ODE Cash Karp 5th Order.vi」は、[確度]に応じて独立変数軸(時間軸)の刻みが調整されている。

8. ODEソルバー VI

VIファイル名:「ODE Solver.vi」

同じ微分方程式に対して解法が切り換えられる。「variable」は可変刻み幅のこと。
0 Runge-Kutta 1 (Euler)
1 Runge-Kutta 2
2 Runge-Kutta 3
3 Runge-Kutta 4
4 Runge-Kutta 23 (variable)
5 Runge-Kutta 45 (variable) (これがデフォルト)
6 BDF (variable)
　(可変刻み幅、可変次数(1～5)、多段、後退微分法(BDF)、別名Gear's法。かたさのほどほどな問題に適す)
7 Adams-Moulton (variable)
　(可変刻み幅、多段、可変次数(1～12)、PECE (予測評価修正評価)モード、Adams-Moulton予測子修正子ペア)
8 Rosenbrock (variable)
　(可変刻み幅、1段、陽解法。かたい問題の一部に適す)
9 Discrete States Only
　(?????)

微分方程式は、「フォーミュラ文字列として与える方法」と「 VIリファレンスとして与える方法」とがある。

8.1 この微分方程式を解く

x'= y
y' = t - x
という連立微分方程式を

x(0) = 0
y(0) = 0
という初期条件で

t = 0から7.5まで解く。

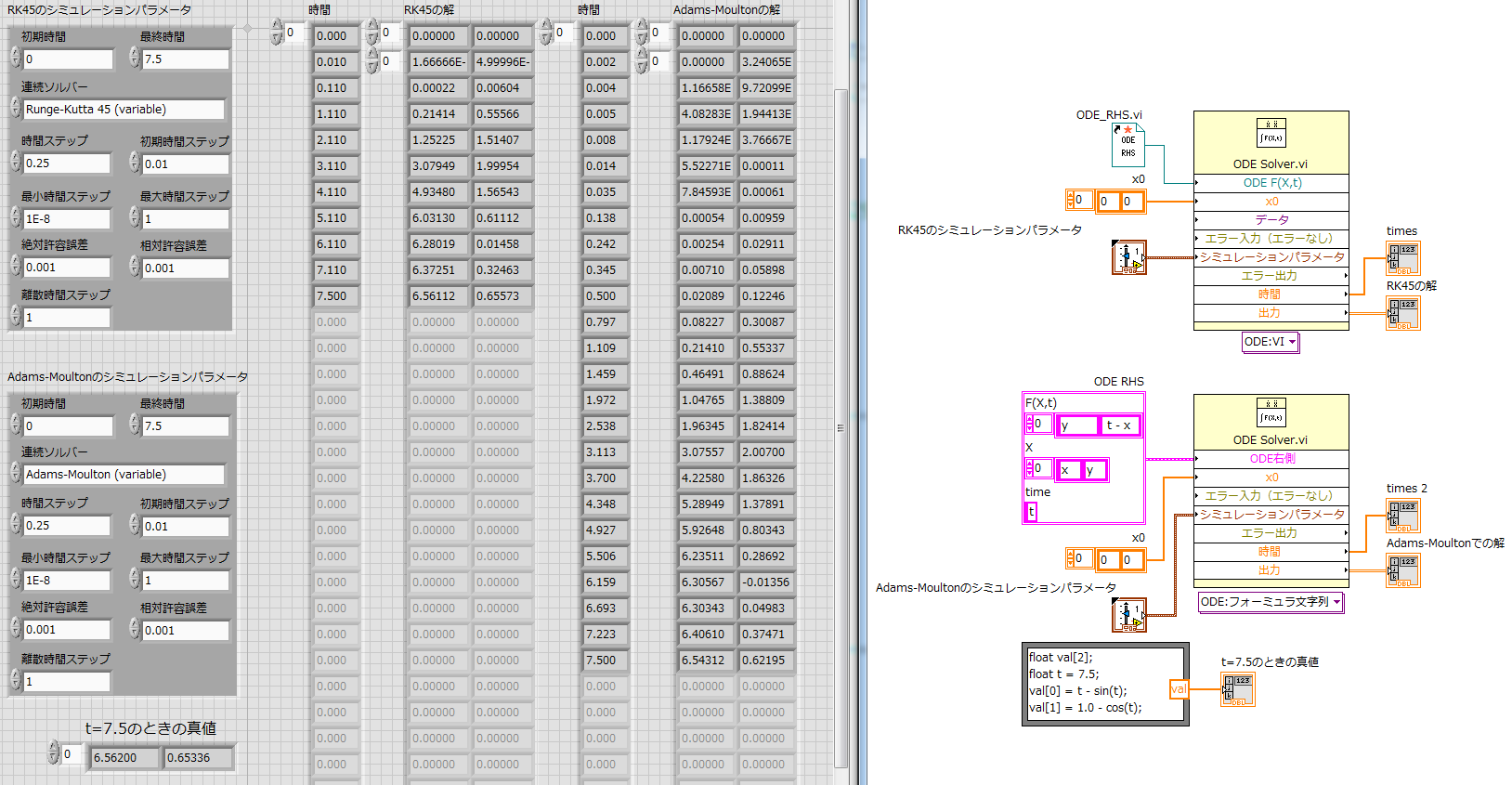
8.2 サンプルVI

比較の手段として、解法の違う2つのVIを1つのサンプルVIにまとめた。一方の方程式をVIリファレンスとして与え、もう一方をフォーミュラ文字列として与えているが、これはサンプルとして示しているだけであって、どちらでもよい。

メインVI: https://drive.google.com/open?id=1coIh1C71IfWOYeG29G-vUmeEAB2dlC2z
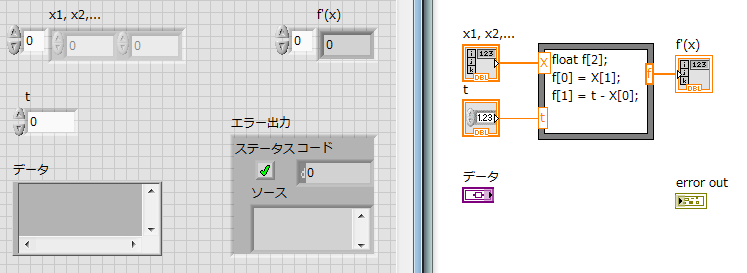
VIリファレンスとして使ったサブVI: https://drive.google.com/open?id=1USPlD68xHeZtGQfBy_EuuPeQnMJMYuiw

9. DAE 5次Radau法 VI (微分代数方程式の解法)

VIファイル名:「DAE Radau 5th Order.vi」

9.1 この微分代数方程式を解く

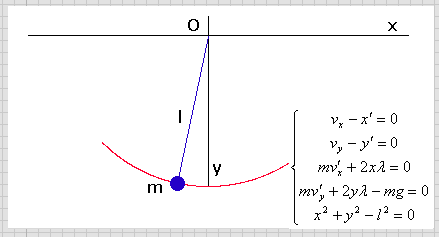
方程式の立て方がわからないので、LabVIEWに同梱してある出来合いのサンプルファイル(単振り子のシミュレーション)から動画化の部分を削ったVIを試してみる。

単振り子の場合は極座標で運動方程式を立てるのが一般的であるが、ここでは下のように直交座標で微分代数方程式を組み立てる。
x^2 + y^2 - l^2 = 0 が拘束条件。
その拘束条件による作用がλ。

9.2 サンプルVI

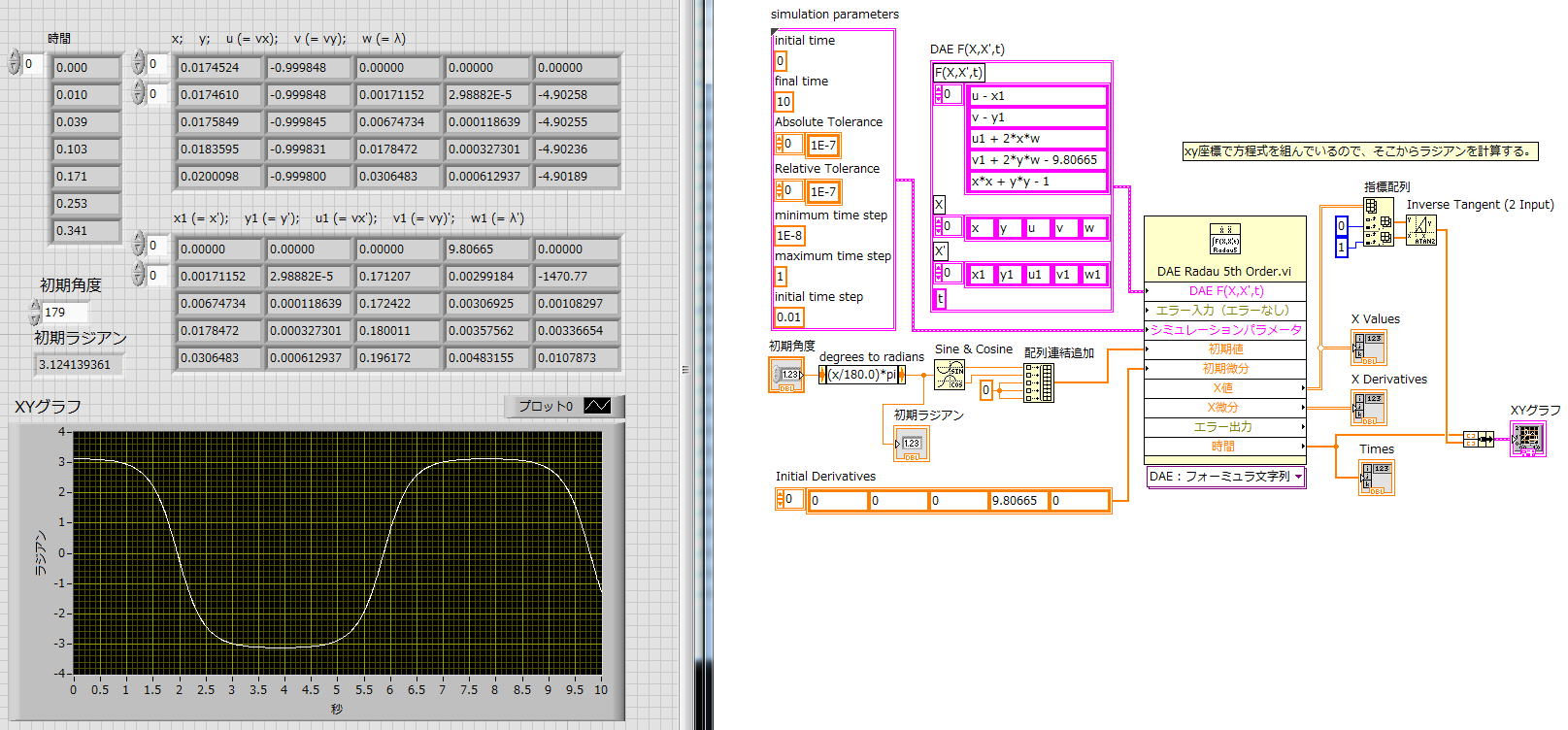
https://drive.google.com/open?id=1Vb0WHs1l0oc7UOC5vrYF5KEvnc3i4ijp
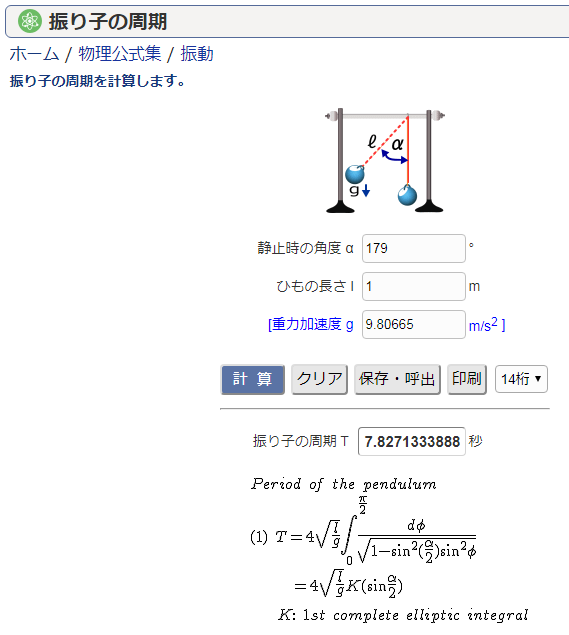
振り子の運動をシミュレートしてみる。初期角度はほぼ真上(179°)、棒の長さは1とした。下のグラフは横軸が秒数、縦軸がラジアンである。等時性の破れがはっきり現れている。

9.3 カシオ高精度計算サイトによる検算

https://keisan.casio.jp/exec/system/1166754115