非対称暗号(公開鍵暗号)といえば、RSA!
はじめに
2025年10月のプロジェクトマネージャ試験受験を終え、2026年春の情報処理安全確保支援士に向けて勉強中です。
セキュリティに関して無知であるため、資格勉強の傍ら暗号技術入門 第3版 秘密の国のアリスを読んでいます。
本記事は、そんなセキュリティ初心者による読書感想文です。
目的
公開鍵暗号について学びます。
対象
公開鍵暗号についてザックリとしたイメージをとらえたい方が対象になります。
公開鍵暗号はコインロッカー
コインロッカーは、コインを入れることでロッカーを閉めることができ、キーによってロッカーを開けることができます。
つまり、コインロッカーにとって、コインはロッカーを閉じるための鍵であり、キーはロッカーを開けるための鍵です。
公開鍵を上記と同様、平文を暗号化するときの鍵と暗号文を復号するときの鍵は別物です。
鍵配送問題
対称鍵暗号で問題になっていた「鍵自体を安全に配送できない問題」は一般的に鍵配送問題と呼ばれます。
鍵配送問題を解決するための方法は下記の通りいくつかあります。
- 鍵の事前共有による解決
- 鍵配布センターによる解決
- Diffie-Hellman 鍵交換による解決
- 公開鍵暗号による解決
鍵の事前共有による解決
鍵配送問題を解決するための最も簡単な方法は「安全な方法で、鍵を前もって渡しておく」という方法です。
これを鍵の事前共有と呼びます。
しかし、この方法では限界があります。
鍵の事前共有の限界
鍵の事前共有では、安全な方法で相手に渡さなくてはいけません。
しかし、ネットワークを通じて鍵を配送すると途中で盗聴される危険性などのリスクが存在します。
また、たとえ鍵の事前共有が可能だとしても、人数が多くなればなるほど膨大な鍵が必要になってしまいます。
例えば、1000人の社員を抱える組織にて、自身の鍵を配送する場合、自身以外の999人に配送する必要があります。
対称鍵暗号で必要になる鍵の数は「n × (n - 1) ÷ 2」なので、
1000 × 999 ÷ 2 = 49万9500個
となります。
「n × (n - 1) ÷ 2」は基本情報や応用情報でも頻出です!
鍵配布センターによる解決
鍵の事前共有の限界を受け、通信用の鍵を作成する鍵配布センター(KDC(= KeyDistributionCenter))を用意する方法もあります。
暗号通信が必要になるたびに、各人は鍵配布センターとの間だけで鍵を事前共有します。
鍵配布センターを使った方法は有効ですが、こちらの方法も限界があります。
鍵配布センターの限界
鍵配布センターは暗号通信を行うたびに下記のような手順を実施する必要があります。
- 通信をしたい人からの申し出があります。
- 鍵配布センターは疑似乱数生成器を使い、セッション鍵を作ります。
- 鍵配布センターは送信者の鍵でセッション鍵を暗号化し、送信者に鍵を送付します。
- 鍵配布センターは受信者の鍵でセッション鍵を暗号化し、受信者に鍵を送付します。
- 送信者は鍵を復号化し、セッション鍵を得ます。
- 受信者は鍵を復号化し、セッション鍵を得ます。
- 受信者は送信者から受信した暗号文を復号化したセッション鍵で復号化します。
- お互いのセッション鍵を削除します。
つまり、鍵配布センターの負担が大きくなってしまい、鍵配布センターのコンピュータが故障すると暗号通信がマヒしてしまいます。
Diffie-Hellman 鍵交換による解決
この方法は送信者と受信者が情報を相互に受け渡しをするという方法です。
この情報によって、両者は同じ鍵を作り出すことができます。
しかし、この情報は攻撃者によって盗聴されたとしても、受信者や送信者と同じ鍵を作り出すことはできません。
公開鍵暗号による解決
対称鍵暗号では「暗号化の鍵」と「復号化の鍵」は同じものですが、公開鍵暗号では「暗号化の鍵」と「復号化の鍵」は別のものです。
復号化できるのは「復号化の鍵」を持っている人だけですが、暗号化は誰でも出来ます。
受信者は前もって自身の「暗号化の鍵」を送信者に知らせておき、受信者だけが持っている「復号化の鍵」を使って暗号文を復号します。
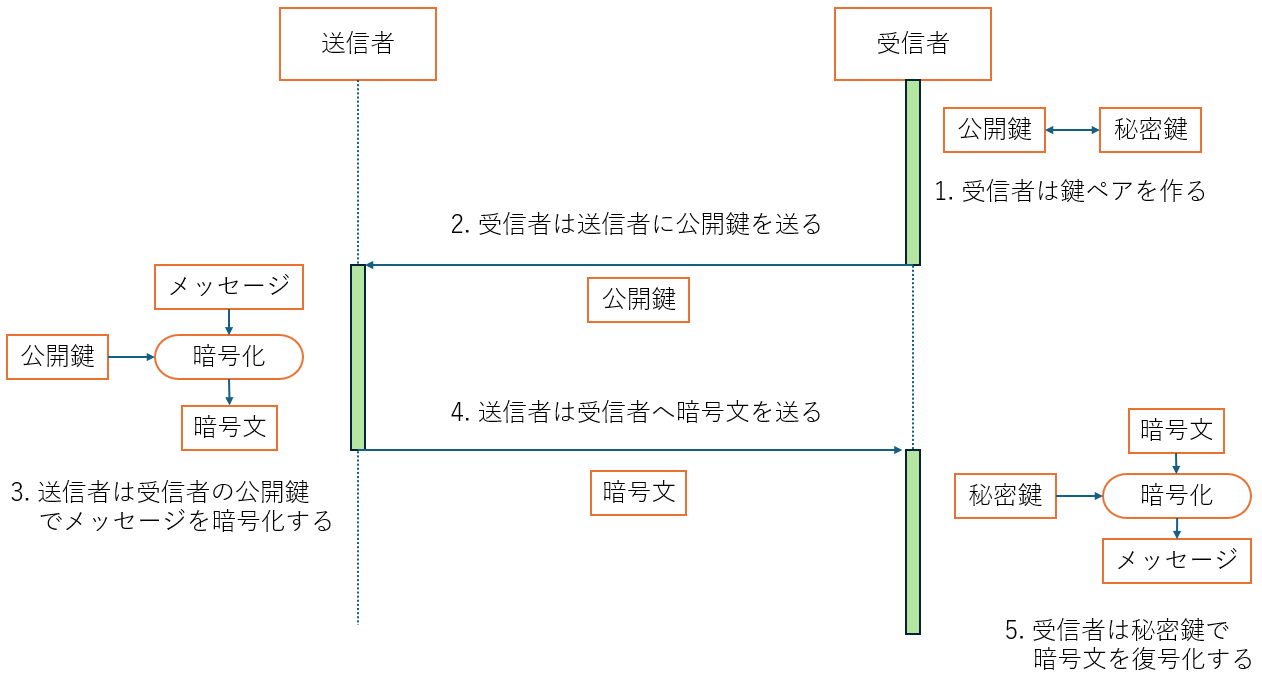
公開鍵暗号
対称鍵暗号とは異なり、異なる鍵で暗号化と復号をする暗号アルゴリズムです。
公開鍵暗号の流れは下記の通りです。
- 受信者は「復号化の鍵(秘密鍵)」と「暗号化の鍵(公開鍵)」の鍵ペアを作成
- 暗号通信が必要なとき、受信者は送信者に対して公開鍵を共有
- 送信者は公開鍵を用いて、平文を暗号化
- 送信者は暗号文を受信者に送付
- 受信者は暗号文を自身の秘密鍵を用いて、暗号文を復号
秘密鍵はその名の通り、秘密にしておかなくてはいけないものであり、ペアの公開鍵で暗号化されたメッセージを復号できます。
一方で、公開鍵は公開してもよい鍵であり、復号化はできず暗号化のみできます。
つまり、公開鍵が攻撃者に知られたとしても復号できません。
公開鍵暗号でも解決できない問題
公開鍵暗号によって、鍵配送問題は解決しました。
しかし、公開鍵が正しい公開鍵かどうかを判断する必要があります。
つまり、公開鍵の認証が必要になります。
また、公開鍵暗号は対称暗号に比べて処理速度が何百倍も遅いという問題もあります。
時間計算
1本しか針がない掛け時計を思い浮かべてください。
加算
針が7を指しているとして、右に20メモリ進めると針がどこを指していますか?
すぐには計算できないですが、下記の計算をするとすぐに結果が分かります。
(7 + 20) ÷ 12 = 27 ÷ 12 = 2 あまり 3
つまり、3を指すことが分かります。
modの計算
modは「余りを求める計算」であり、割り算をした結果の余りが答えになります。
たとえば、下記のような計算の時、数学者は「27と3は12を法として合同である」と表現します。
27 mod 12 = 3
減算
modを使った減算では下記の□を埋めることです。
答えは、「□ = 5」ですが、「7は-5と同じ役割」であることが分かります。
(7 + □) mod 12 = 0
[(X + Y) mod 12 = 0になるXとYの対応表]
| X | Y | 結果 |
|---|---|---|
| 0 | 0 | 0 |
| 11 | 1 | 0 |
| 10 | 2 | 0 |
| 9 | 3 | 0 |
| 8 | 4 | 0 |
| 7 | 5 | 0 |
| 6 | 6 | 0 |
| 5 | 7 | 0 |
| 4 | 8 | 0 |
| 3 | 9 | 0 |
| 2 | 10 | 0 |
| 1 | 11 | 0 |
乗算
加算を繰り返したものです。
乗算も同様の考えができ、掛け算の結果に対してmodを取ります。
例えば、下記だと4を得られます。
7 × 4 mod 12 = 28 mod 12 = 4
除算
modを使った除算では下記□を埋めることです。
計算してみると、□が7のときのみ割り切れます。
7 × □ mod 12 = 1
しかし、これもすぐには答えが出てきません。
ここで、「mod 12」を隠すと、「7 × □ = 1」となり、逆数であることが分かります。
逆数とは、かけると1になる数のことです(今回の場合、「12を法とする世界」を前提とします)。
「7 × □ mod 12 = 1」の時、逆数をしべてみると下記の通り「1, 5, 7, 11」であることが分かります。
実は逆数を求めるとき、その数と12の最大公約数が1であるかどうかで判断できます。
これを数学では、12と互いに素な数と呼びます。
1 × □ mod 12 = 1 → □ = 1
2 × □ mod 12 = 1 → □ は存在しない
3 × □ mod 12 = 1 → □ は存在しない
4 × □ mod 12 = 1 → □ は存在しない
5 × □ mod 12 = 1 → □ = 5
6 × □ mod 12 = 1 → □ は存在しない
7 × □ mod 12 = 1 → □ = 7
8 × □ mod 12 = 1 → □ は存在しない
9 × □ mod 12 = 1 → □ は存在しない
10 × □ mod 12 = 1 → □ は存在しない
11 × □ mod 12 = 1 → □ = 11
累乗
乗算は加算を繰り返したものであり、累乗は乗算を繰り返したものです。
例えば、7^4は下記で求められます。
7^4 mod 12 = 7 × 7 × 7 × 7 mod 12
= 2401 mod 12 = 1
上記の場合、「7 × 7 × 7 × 7 mod 12」は「7 × 7 mod 12」を2回かけたものと考えられます。
7^4 mod 12 = 7 × 7 × 7 × 7 mod 12
= ((7 × 7 mod 12) × (7 × 7 mod 12)) mod 12
= ((49 mod 12) × (49 mod 12)) mod 12
= (1 × 1) mod 12
= 1 mod 12
= 1
途中でmodを取らないと大きな数の積を計算しなくてはならず、計算量が膨大になってしまいます。
途中でmodを取る積は、RSAの暗号化/復号化でも使われる方法です。
対数
累乗の逆演算は、対数と呼ばれ、通常の対数は下記で求められます。
□は2が入りますね。
7^□ = 49
離散対数
時計演算における対数は、離散対数と呼ばれ、下記で求められます。
□には、9が入ります。
7^□ mod 13 = 8
離散対数は、数が大きくなると計算量が多く、求めるためには非常に時間がかかります。
また、離散対数を求める高速なアルゴリズムは見つかっていません。
離散対数は、DiffieHellman鍵交換や公開鍵アルゴリズムの一つであるElGamal方式で使われます。
RSA
公開鍵暗号では、「暗号化の鍵」と「復号化の鍵」を分けます。
RSAは開発者3名の名前の頭文字をとってつけられました。
RSAによる暗号化
RSAによる暗号化では、下記の通り「平文を表す数をE乗し、mod Nを取ったもの」です。
暗号文 = 平文^E mod N
EとNが分かれば、だれでも暗号化を行うことができます。
したがって、EとNがRSAにおける暗号化の鍵であり、すなわち公開鍵です。
つまり、EとNが公開鍵の鍵ペアといえます。
RSAによる復号化
RSAによる復号化では、下記の通り「暗号文を表す数をD乗し、mod Nを取ったもの」です。
平文 = 暗号文^D mod N
DとNが分かれば、だれでも復号できます。
したがって、DとNがRSAにおける復号化の鍵であり、すなわち秘密鍵です。
つまり、DとNが秘密鍵の鍵ペアといえます。
鍵ペアを作る
RSAの鍵ペアの作成手順は下記の通りです。
- Nを求める
- Lを求める(Lは鍵ペア生成のときのみ登場する数です。)
- Eを求める
- Dを求める
Nを求める
疑似乱数生成器などで大きな素数p, qを作成し、下記の通りNを求めます。
N = p × q
Lを求める
Lは、p-1とq-1の最小公倍数(lcm(= LeastCommonMultiple))であり、下記のように求めます。
L = lcm(p - 1, q - 1)
Eを求める
Eは1よりも大きく、Lよりも小さな数でなければなりません。
また、EとLとの最大公約数(gcd(= GreatestCommonDivisor))である必要があり、下記のように求めます。
1 < E < L
gcd(E, L) = 1
Dを求める
DはEから計算する必要があり、下記の通りです。
1 < D < L
E × D mod L = 1
RSAへの攻撃
RSAでは、暗号解読者は平文を復元できるのでしょうか。
上記を考える前に、暗号解読者が知っていることと知らないことを整理してみます。
<暗号解読者が知っていること>
- 暗号文
- 数EとN
→ 公開鍵として公開されている鍵ペア
<暗号解読者が知らないこと>
- 平文
- 数D
- そのほか
→ 鍵ペア作成時のp, q, L
暗号文から平文を求める
暗号文の公式から平文を直接求めるには、「N を法とする e 乗根を計算する必要」があります。
これは、背後にある N の素因数 p, q を知っていれば簡単にできますが、公開情報(N, E)だけから p, q を見つける=大きな整数を因数分解する問題は非常に難しいと考えられています。
RSA の安全性は、この「大きな整数の因数分解問題」の困難さに依存しています。
man-in-the-middle攻撃(MITM攻撃)
RSAを解読することはできませんが、機密性に対する非常に有効な攻撃方法です。
この攻撃は、攻撃者が送信者と受信者の間に入り込み、送信者に対しては受信者のように、受信者に対しては送信者のようになりすます攻撃です。
この攻撃はどんな暗号にも使え、機密性は保っている状態です。
ただし、送信者と攻撃者、攻撃者と受信者の間の機密性を保っているという意味です。
このMITM攻撃を防ぐためには、公開鍵が送信者のものであるかどうか認証が必要になります。
この役割が証明書です。
選択暗号文攻撃
任意のデータを送信すると、暗号文とみなし復号し、返信するサービス(復号オラクル)を攻撃者が利用できることを仮定した攻撃です。
つまり、様々なデータを復号オラクルに送信することで、データの不正個所(エラー)を返信するため、攻撃者はエラー内容を解読し、暗号文を解読するヒントを得ます。
したがって、「正しい平文でないと暗号文を作ることができない」ことを判定する機能を追加した改良版RSA(= RSA-OAEP(= OptimalAsymmetricEncryptionPadding))という暗号化アルゴリズムが考えられました。
他の公開鍵暗号
ElGamal方式
エルガマル方式と呼ばれ、mod Nで離散対数を求めるのが困難なことを利用しています。
一方で、RSAは素因数分解が困難なことを利用しています。
この方式には、暗号文の長さが平文の2倍になってしまうという欠点があります。
Rabin方式
ラビン方式と呼ばれ、mod Nで平方根を求めるのが困難なことを利用しています。
この方式は、素因数分解を行うのと同じだけの困難さがあることが証明されています。
楕円曲線暗号
ECC(ElipticCurveCryptography)と呼ばれ、RSAよりも鍵のビット数を少なくできるのが特徴です。
楕円曲線と呼ばれる曲線を求め、その曲線の上に乗っている点に対して、特殊な「乗算」を定義します。
この特殊な「乗算」の逆演算が難しいことを利用しています。