【E資格】part4 深層学習Day2

深層学習 Day2

本記事はラビット☆チャレンジのレポートとして記載し、今回は以下の内容について記述する。

Section1：勾配消失問題
Section2：学習率最適化手法
Section3：過学習
Section4：畳み込みニューラルネットワークの概念
Section5：最新のCNN

動画の要約

Section1：勾配消失問題

1. 勾配消失問題とは

• 誤差逆伝播法か下位層に進んでいくに連れて、勾配がどんどん緩やかになっていく。
• そのため、勾配降下法による、更新では下位層のパラメータはほとんど変わらず、訓練は最適値に収束しなくなる。
• 対策として下記の3つの方法がある
  • 活性化関数の選択
  • 重みの初期値設定
  • バッチ正規化

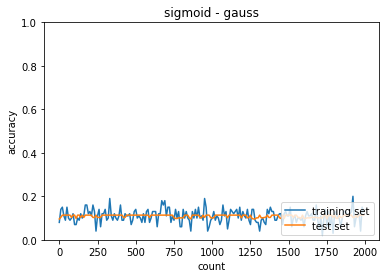
活性化関数として、シグモイド関数を用いると大きな値では出力の変化が微小なため、ReLU関数を用いられることが多い。

2)重みの初期値設定

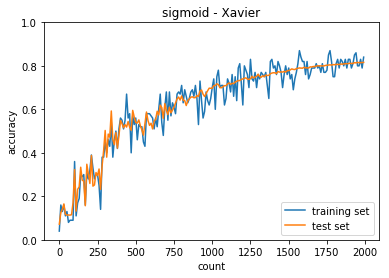
設定方法としてXavierとHeが用いられる。

• Xavier
  • 設定方法：重みの要素を、前の層のノード数の平方根で除算した値を用いる
  • 活性化関数
    • ReLU関数
    • シグモイド(ロジスティック)関数
    • 双曲線正接関数
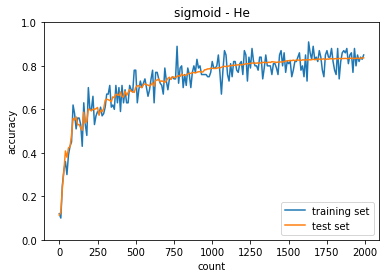
• He
  • 設定方法：重みの要素を、前の層のノード数の平方根で除算した値に$\sqrt{2}$をかけた値
  • 活性化関数
    • ReLu関数

3)バッチ正規化

• バッチ正規化とは？
  • ミニバッチ単位で、入力値のデータの偏りを抑制する手法
• バッチ正規化の使い所とは?
  • 活性化関数に値を渡す前後に、バッチ正規化の処理を孕んだ層を加える

Section2：学習率最適化手法

1. 学習率とは

• 勾配降下法で学習を収束させるための係数
• 学習率が大きいと収束が早いが、最適値にいつまでもたどり着かず発散してしまう
• 学習率が小さいと発散することはないが収束するまでに時間がかかる。大域局所最適値に収束しづらい

1. 学習率最適化手法

• モメンタム
  • 誤差をパラメータで微分したものと学習率の積を減算した後、現在の重みに前回の重みを減算した値と慣性の積を加算する
  • 局所的最適解にはならず、大域的最適解となる
  • 谷間についてから最も低い位置(最適値)にいくまでの時間が早い
• AdaGrad
  • 誤差をパラメータで微分したものと再定義した学習率の積を減算する
  • 勾配の緩やかな斜面に対して、最適値に近づける
  • 学習率が徐々に小さくなるので、鞍点問題を引き起こす可能性がある
• RMSProp
  • 誤差をパラメータで微分したものと再定義した学習率の積を減算する
  • 局所的最適解にはならず、大域的最適解となる
  • ハイパーパラメータの調整が必要な場合が少ない
• Adam
  • モメンタムの、過去の勾配の指数関数的減衰平均
  • RMSPropの、過去の勾配の2乗の指数関数的減衰平均
  • モメンタムおよびRMSPropのメリットを持つアルゴリズム

Section3：過学習

1. 過学習とは

• テスト誤差と訓練誤差とで学習曲線が乖離すること
• 特定の訓練サンプルに対して、特化して学習する
• 対応方法
  • 正則化
  • ドロップアウト

2)正則化

• ネットワークの自由度を制約すること
• 重みが大きい値を取らないように正則化項を加えて過学習を抑える
• L1正則化とL2正則化手法がある

E_n(w)+ \frac{1}{p}\lambda \|x\|_p 

\|x\|_p  = (|x_1|^p + \dots + |x_n|^p)^\frac{1}{p}

p=1の時、L1正則化と呼び、p=2の時、L2正則化と呼ぶ。

3)ドロップアウト

• ランダムにノードを削除して学習させること
• データ量を変化させずに、異なるモデルを学習させていると解釈できる

Section4：畳み込みニューラルネットワークの概念

• 中間層に畳み込み層とプーリング層をもつニューラルネットワーク
• 主に画像認識で用いられることが多い
• 計算量が多い

畳み込み層とプーリング層について

• 畳み込み層
  • 画像の場合、縦、横、チャンネルの3次元のデータをそのまま学習し、次に伝えることができる
  • フィルターを通して出力されたものにバイアスを加えて画像の特徴を抽出する
  • パディングを用いて、画像のサイズを維持したり端の情報を取得する
  • 画像を小さくする場合はストライドを大きくする
  • チャンネルを用いることで３次元データとなる
• プーリング層
  • Max値を取るものと平均を取る手法がある
  • 画像の特徴を残しつつサイズを小さくする
  • サイズを小さくすることで計算量を減らすことが可能

Section5：最新のCNN(AlexNet)

• 2012年に開かれた画像認識コンペティションで2位に大差をつけて優勝したモデル
• ディープラーニングが大きく注目を集めたきっかけとなったモデル
• 5層の畳み込み層およびプーリング層など、それに続く3層の全結合層から構成される
• サイズ4096の全結合層の出力にドロップアウトを使用することで過学習を抑える

確認テスト

P12 連鎖律の原理を使い、$\frac{dz}{dx}$を求めよ。

z = t^2,t = x+y

連鎖律を用いて計算する。

\frac{dz}{dx} =\frac{dz}{dt} \frac{dt}{dx}=2t \cdot 1 =2t

P20 シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値として正しいものを選択肢から選べ。
（1）0.15
（2）0.25
（3）0.35
（4）0.45
＜答え＞
(2)

f(x) = \frac{1}{1+e^{-x}}

f^{\prime}(x) = (1-f(x))\cdot f(x)

f^{\prime}(0) = (1-f(0))\cdot f(0)= 2^{-2} = 0.25

P28 重みの初期値に0を設定すると、どのような問題が 発生するか。簡潔に説明せよ。

• 2層目の逆伝播ですべて均一な重みをもつようになってしまう
• 勾配降下法が有効でなくなる

P31 一般的に考えられるバッチ正規化の効果を2点挙げよ。

• 勾配消失が起きづらくなる
• 計算が高速化される

P47 モメンタム・AdaGrad・RMSPropの特徴をそれぞれ簡潔に説明せよ。

• モメンタム
  • 谷間についてから最も低い位置(最適値)にいくまでの時間が早い
• AdaGrad
  • 勾配の緩やかな斜面に対して、最適値に近づける
• RMSProp
  • ハイパーパラメータの調整が必要な場合が少ない

P63
機械学習で使われる線形モデル(線形回帰、主成分分析・・・etc)の正則化は、モデルの重みを制限することで可能となる。 前述の線形モデルの正則化手法の中にリッジ回帰という手法があり、その特徴として正しいものを選択しなさい。

(a) ハイパーパラメータを大きな値に設定すると、すべての重みが限りなく0に近づく
(b) パイパーパラメータを0に設定すると、非線形回帰となる
(c) バイアス項についても、正則化される
(d) リッジ回帰の場合、隠れ層に対して正則化項を加える

＜答え＞
(a)

P68 下図について、L1正則化を表しているグラフは どちらか答えよ。

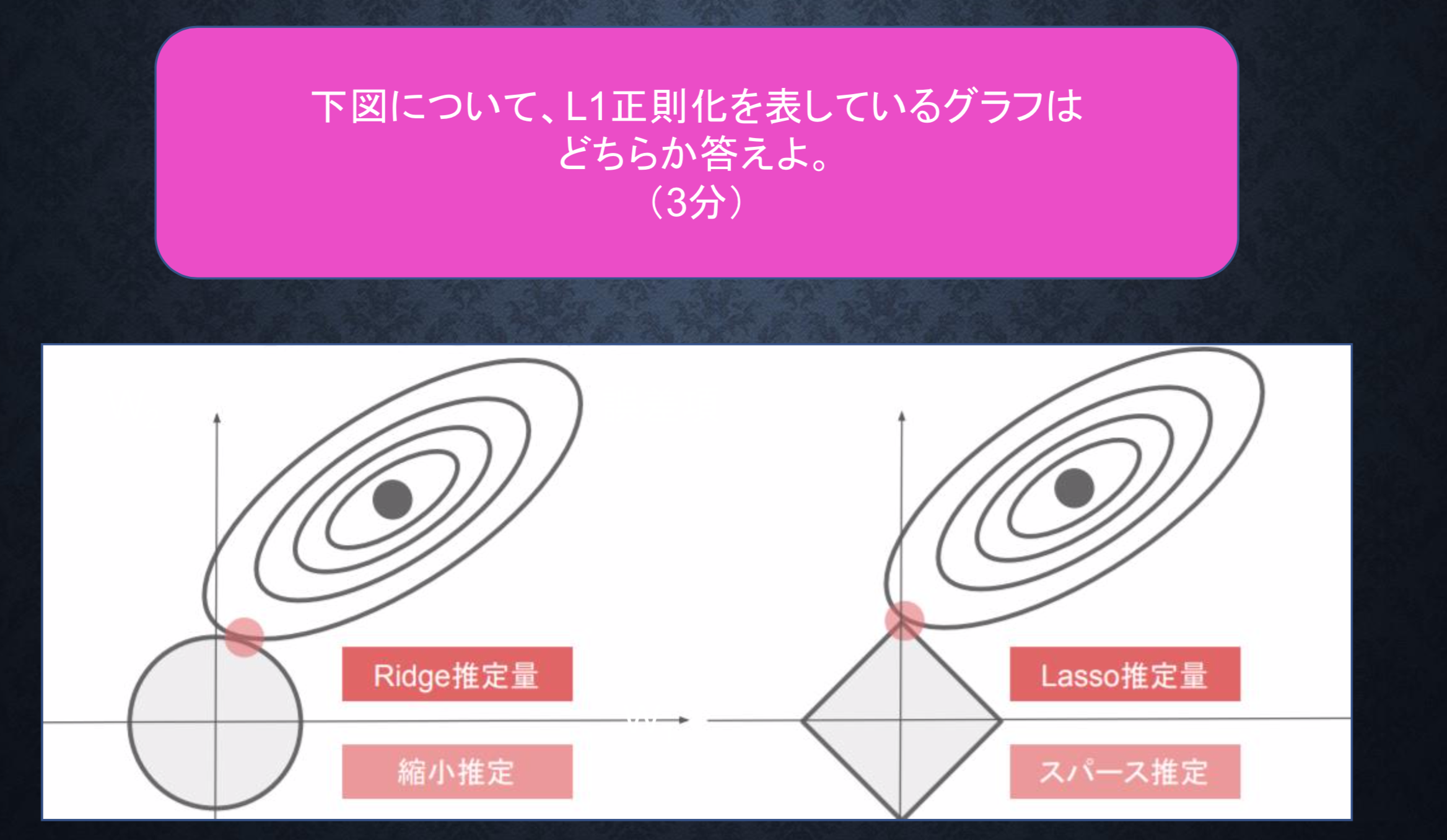
右のグラフがL1正則化を表す。

P100 サイズ6×6の入力画像を、サイズ2×2のフィルタで畳み込んだ時の出力画像のサイズを答えよ。 なおストライドとパディングは1とする。

＜答え＞
6×6のパディングで8×8となり、2×2のフィルタでストライド1で畳み込むと7×7になる。

演習問題

vanishing gradientを編集して勾配消失について理解する。

import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from data.mnist import load_mnist
from PIL import Image
import pickle
from common import functions
import matplotlib.pyplot as plt

# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)

print("データ読み込み完了")

# 重み初期値補正係数
wieght_init = 0.01
#入力層サイズ
input_layer_size = 784
#中間層サイズ
hidden_layer_1_size = 40
hidden_layer_2_size = 20

#出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 2000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval=10

# 初期設定
def init_network():
    network = {} 

    ###########  変更箇所  ##############

    # Xavierの初期値
    network['W1'] = np.random.randn(input_layer_size, hidden_layer_1_size) / (np.sqrt(input_layer_size))
    network['W2'] = np.random.randn(hidden_layer_1_size, hidden_layer_2_size) / (np.sqrt(hidden_layer_1_size))
    network['W3'] = np.random.randn(hidden_layer_2_size, output_layer_size) / (np.sqrt(hidden_layer_2_size))

    # Heの初期値
    #network['W1'] = np.random.randn(input_layer_size, hidden_layer_1_size) / np.sqrt(input_layer_size) * np.sqrt(2)
    #network['W2'] = np.random.randn(hidden_layer_1_size, hidden_layer_2_size) / np.sqrt(hidden_layer_1_size) * np.sqrt(2)
    #network['W3'] = np.random.randn(hidden_layer_2_size, output_layer_size) / np.sqrt(hidden_layer_2_size) * np.sqrt(2)
        
    #################################
    
    network['b1'] = np.zeros(hidden_layer_1_size)
    network['b2'] = np.zeros(hidden_layer_2_size)
    network['b3'] = np.zeros(output_layer_size)

    return network

# 順伝播
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    ###########  変更箇所  ##############
    
    hidden_f = functions.relu
    
    #################################
    
    u1 =  np.dot(x, W1) + b1
    z1 = hidden_f(u1)
    u2 =  np.dot(z1, W2) + b2
    z2 = hidden_f(u2)
    u3 =  np.dot(z2, W3) + b3
    y = functions.softmax(u3)
 
    return z1, z2, y

# 誤差逆伝播
def backward(x, d, z1, z2, y):
    grad = {}
    
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    ###########  変更箇所  ##############
    
    hidden_d_f = functions.d_relu
    
    #################################
    
    # 出力層でのデルタ
    delta3 = functions.d_softmax_with_loss(d, y)
    # b3の勾配
    grad['b3'] = np.sum(delta3, axis=0)
    # W3の勾配
    grad['W3'] = np.dot(z2.T, delta3)
    # 2層でのデルタ
    delta2 = np.dot(delta3, W3.T) * hidden_d_f(z2)
    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    # 1層でのデルタ
    delta1 = np.dot(delta2, W2.T) * hidden_d_f(z1)
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)

    return grad

# パラメータの初期化
network = init_network()

accuracies_train = []
accuracies_test = []

# 正答率
def accuracy(x, d):
    z1, z2, y = forward(network, x)
    y = np.argmax(y, axis=1)
    if d.ndim != 1 : d = np.argmax(d, axis=1)
    accuracy = np.sum(y == d) / float(x.shape[0])
    return accuracy

for i in range(iters_num):
    # ランダムにバッチを取得    
    batch_mask = np.random.choice(train_size, batch_size)
    # ミニバッチに対応する教師訓練画像データを取得    
    x_batch = x_train[batch_mask]
    # ミニバッチに対応する訓練正解ラベルデータを取得する
    d_batch = d_train[batch_mask]


    
    z1, z2, y = forward(network, x_batch)
    grad = backward(x_batch, d_batch, z1, z2, y)

    if (i+1)%plot_interval==0:
        accr_test = accuracy(x_test, d_test)
        accuracies_test.append(accr_test)
        
        accr_train = accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)

        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
        
    # パラメータに勾配適用
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        network[key]  -= learning_rate * grad[key]


lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
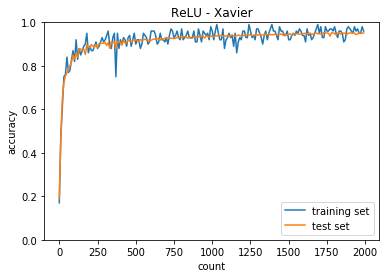
plt.title("ReLU - Xavier")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()

正答率(トレーニング) = 0.13
正答率(テスト) = 0.1135

正答率(トレーニング) = 0.84
正答率(テスト) = 0.816

正答率(トレーニング) = 0.85
正答率(テスト) = 0.8369

隠れ層のノードは40-20。
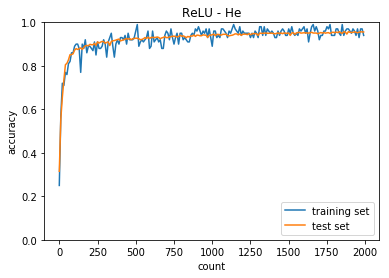
正答率(トレーニング) = 0.95
正答率(テスト) = 0.9266

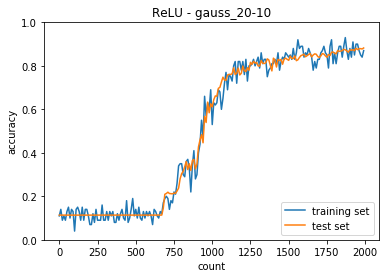
隠れ層のノードを20-10に変更した。
正答率(トレーニング) = 0.87
正答率(テスト) = 0.8822

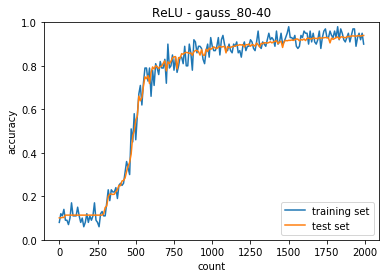
隠れ層のノードを80-40に変更した。
正答率(トレーニング) = 0.9
正答率(テスト) = 0.9399

正答率(トレーニング) = 0.94
正答率(テスト) = 0.9558

正答率(トレーニング) = 0.96
正答率(テスト) = 0.9521

考察

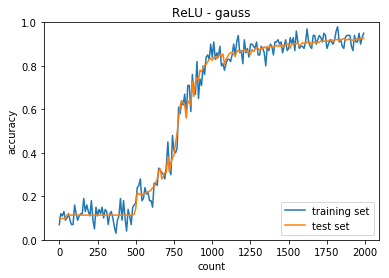
• 中間層の活性化関数がシグモイドとReLUで収束するまでの動きが異なること
• ReLU関数の方が急激に収束する
• 重みの初期値によっても収束するまでの挙動が異なる
• ReLU - Xiavier では今回のケースは訓練回数が少なくても収束する
• 隠れ層のノードを増やした方が早く収束した

optimizerを編集して最適化について理解する。

import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet


# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)

print("データ読み込み完了")

# batch_normalizationの設定 ================================
#use_batchnorm = True
use_batchnorm = False
# ====================================================


network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std='He',
                       use_batchnorm=use_batchnorm)

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    # 勾配
    grad = network.gradient(x_batch, d_batch)
    
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        network.params[key] -= learning_rate * grad[key]
        
        loss = network.loss(x_batch, d_batch)
        train_loss_list.append(loss)
    
    
    if (i + 1) % plot_interval == 0:
        accr_test = network.accuracy(x_test, d_test)
        accuracies_test.append(accr_test)        
        accr_train = network.accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)
        
        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))

print('学習率：'+str(learning_rate))

lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
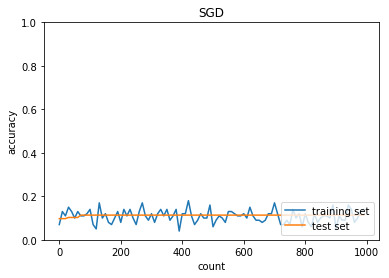
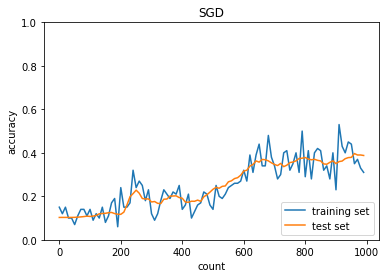
plt.title("SGD")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()

学習率：0.01
バッチ正則化：なし
活性化関数：シグモイド
重みの初期化：0.01
正答率(トレーニング) = 0.14
正答率(テスト) = 0.1135

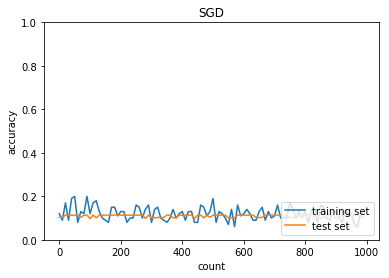
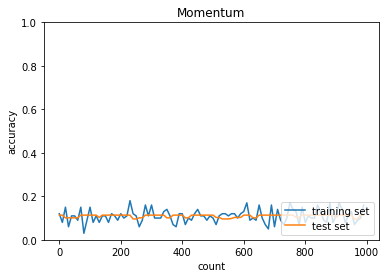
学習率：0.1
バッチ正則化：なし
活性化関数：シグモイド
重みの初期化：0.01
正答率(トレーニング) = 0.13
正答率(テスト) = 0.1028

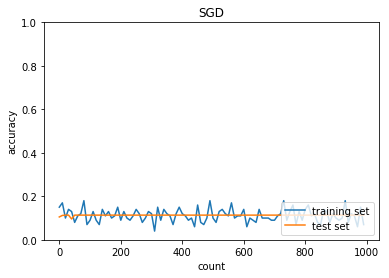
学習率：0.01
バッチ正則化：あり
活性化関数：シグモイド
重みの初期化：0.01
正答率(トレーニング) = 0.59
正答率(テスト) = 0.6223

学習率：0.01
バッチ正則化：なし
活性化関数：ReLU
重みの初期化：0.01
正答率(トレーニング) = 0.07
正答率(テスト) = 0.1135

学習率：0.01
バッチ正則化：なし
活性化関数：シグモイド
重みの初期化：He
正答率(トレーニング) = 0.31
正答率(テスト) = 0.3878

Momentum

学習率：0.01
バッチ正則化：なし
活性化関数：シグモイド
重みの初期化：He
正答率(トレーニング) = 0.16
正答率(テスト) = 0.1135

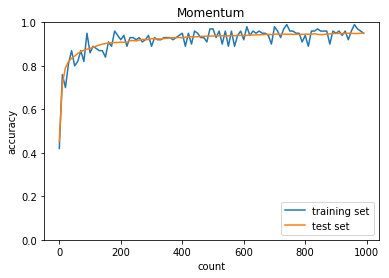
学習率：0.01
バッチ正則化：あり
活性化関数：ReLU
重みの初期化：He
正答率(トレーニング) = 0.95
正答率(テスト) = 0.9502

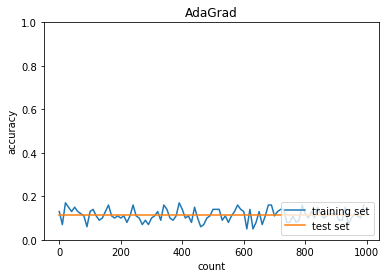
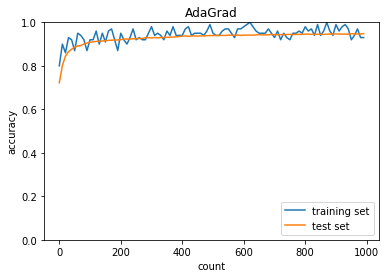
AdaGrad

学習率：0.01
バッチ正則化：なし
活性化関数：シグモイド
重みの初期化：0.01
正答率(トレーニング) = 0.16
正答率(テスト) = 0.1135

学習率：0.01
バッチ正則化：あり
活性化関数：ReLU
重みの初期化：He
正答率(トレーニング) = 0.93
正答率(テスト) = 0.948

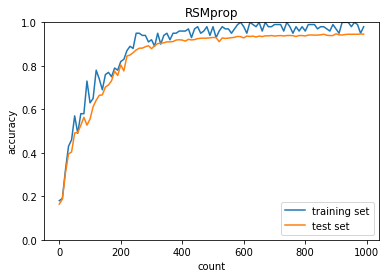
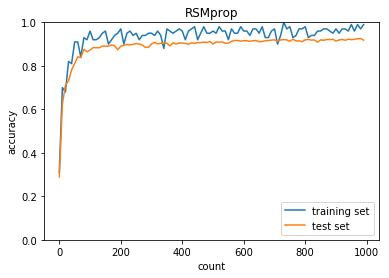
RSMprop

学習率：0.01
バッチ正則化：なし
活性化関数：シグモイド
重みの初期化：0.01
正答率(トレーニング) = 0.98
正答率(テスト) = 0.9454

学習率：0.01
バッチ正則化：あり
活性化関数：シグモイド
重みの初期化：0.01
正答率(トレーニング) = 0.99
正答率(テスト) = 0.9181

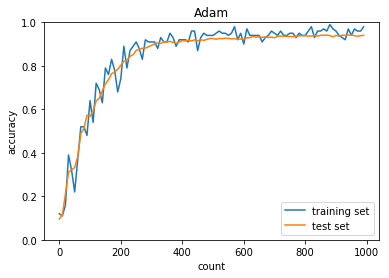
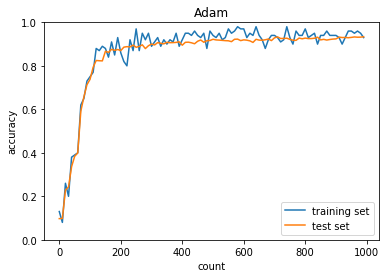
Adam

学習率：0.01
バッチ正則化：なし
活性化関数：シグモイド
重みの初期化：0.01
正答率(トレーニング) = 0.98
正答率(テスト) = 0.9406

学習率：0.03
バッチ正則化：なし
活性化関数：シグモイド
重みの初期化：0.01
正答率(トレーニング) = 0.93
正答率(テスト) = 0.934

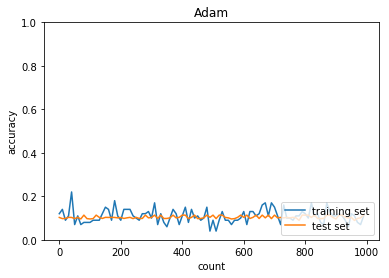
学習率：0.3
バッチ正則化：なし
活性化関数：シグモイド
重みの初期化：0.01
正答率(トレーニング) = 0.11
正答率(テスト) = 0.1135

考察

• 最適化手法ごとに収束の動きが異なる
• 学習率を大きくすると早く収束するが、値が大きいと発散する
• バッチ正則化、活性化関数、重みの初期化について組み合わせて最適なものを選択する必要性を感じた
• Adamは比較的初期のパラメータでも収束するため、実用に用いられやすいことを理解した

overfitingを編集して過学習について理解する。

import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
from common import optimizer


(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)

print("データ読み込み完了")

# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]

network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
optimizer = optimizer.SGD(learning_rate=0.01)

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10


for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    grad = network.gradient(x_batch, d_batch)
    optimizer.update(network.params, grad)

    loss = network.loss(x_batch, d_batch)
    train_loss_list.append(loss)
        
    if (i+1) % plot_interval == 0:
        accr_train = network.accuracy(x_train, d_train)
        accr_test = network.accuracy(x_test, d_test)
        accuracies_train.append(accr_train)
        accuracies_test.append(accr_test)

        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))        

lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
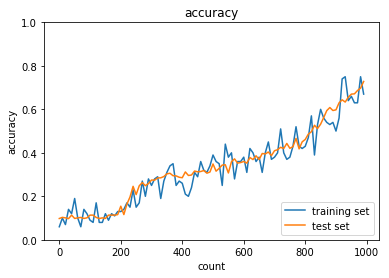
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()

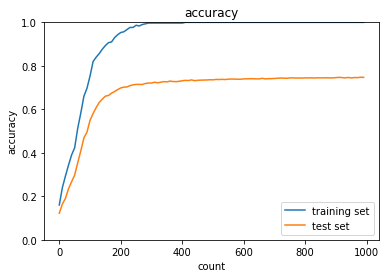
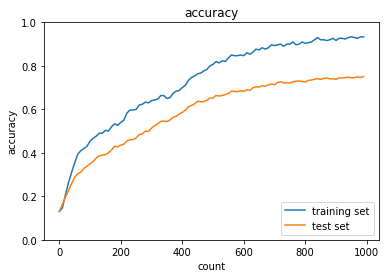
正答率(トレーニング) = 1.0
正答率(テスト) = 0.7471
過学習が発生している。

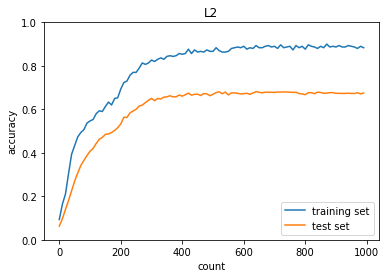
L2正則化後
正答率(トレーニング) = 0.8833333333333333
正答率(テスト) = 0.6753

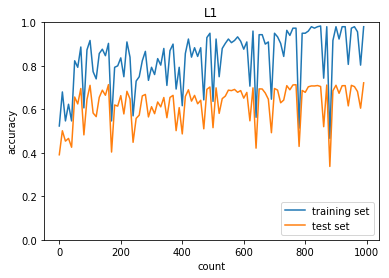
L1正則化後
正答率(トレーニング) = 0.8833333333333333
正答率(テスト) = 0.6753

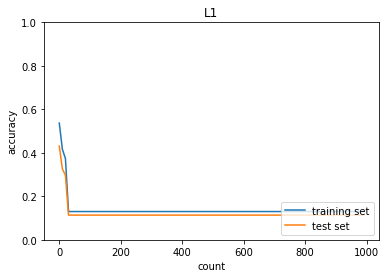
L1正則化で重みを0.005→0.03へ変更
正答率(トレーニング) = 0.13
正答率(テスト) = 0.1135

Dropout

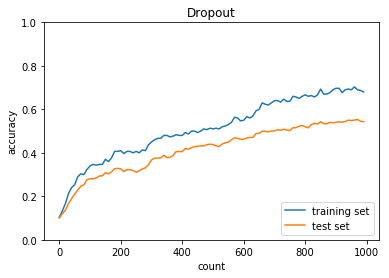
optimizer：SGD
正答率(トレーニング) = 0.68
正答率(テスト) = 0.5434

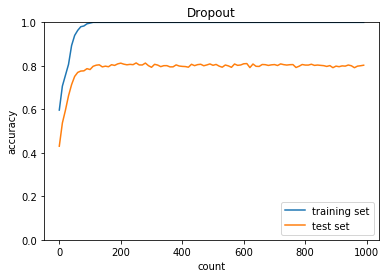
optimizer：Adam
正答率(トレーニング) = 1.0
正答率(テスト) = 0.8029

Dropout　＋　L1正則化

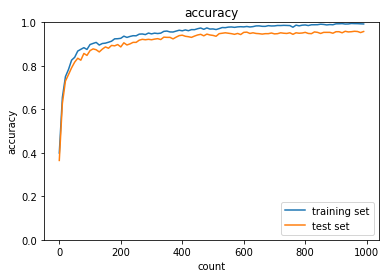
正答率(トレーニング) = 0.9333333333333333
正答率(テスト) = 0.7513

考察

• ノルム正則化、ドロップアウト共に過学習を抑える有効な手段である
• 正則化の重みをあげると学習が進まないことを理解した
• ドロップアウトはドロップアウト率やoptimizerを最適な値にする必要がある

simple_convolution_networkを編集してCNNについて理解する。

import sys, os
sys.path.append (os.pardir)
import pickle
import numpy as np
from collections import OrderedDict
from common import layers
from common import optimizer
from data.mnist import load_mnist
import matplotlib.pyplot as plt

# 画像データを２次元配列に変換
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
    # N: number, C: channel, H: height, W: width
    N, C, H, W = input_data.shape
    out_h = (H + 2 * pad - filter_h) // stride + 1
    out_w = (W + 2 * pad - filter_w) // stride + 1

    img = np.pad (input_data, [(0, 0), (0, 0), (pad, pad), (pad, pad)], 'constant')
    col = np.zeros ((N, C, filter_h, filter_w, out_h, out_w))

    for y in range (filter_h):
        y_max = y + stride * out_h
        for x in range (filter_w):
            x_max = x + stride * out_w
            col [:, :, y, x, :, :] = img [:, :, y:y_max:stride, x:x_max:stride]

    col = col.transpose (0, 4, 5, 1, 2,
                         3)  # (N, C, filter_h, filter_w, out_h, out_w) -> (N, filter_w, out_h, out_w, C, filter_h)

    col = col.reshape (N * out_h * out_w, -1)
    return col

# ２次元配列を画像データに変換
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
    # N: number, C: channel, H: height, W: width
    N, C, H, W = input_shape
    # 切り捨て除算
    out_h = (H + 2 * pad - filter_h)//stride + 1
    out_w = (W + 2 * pad - filter_w)//stride + 1
    col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2) # (N, filter_h, filter_w, out_h, out_w, C)

    img = np.zeros((N, C, H + 2 * pad + stride - 1, W + 2 * pad + stride - 1))
    for y in range(filter_h):
        y_max = y + stride * out_h
        for x in range(filter_w):
            x_max = x + stride * out_w
            img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]

    return img[:, :, pad:H + pad, pad:W + pad]

# im2colの処理確認
input_data = np.random.rand(2, 1, 4, 4)*100//1 # number, channel, height, widthを表す
print('========== input_data ===========\n', input_data)
print('==============================')
filter_h = 2
filter_w = 2
stride = 2
pad = 0
col = im2col(input_data, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
print('============= col ==============\n', col)
print('==============================')
img = col2im(col, input_shape=input_data.shape, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
print(img)

#im2colの処理
============= col ==============
 [[57. 67. 46. 18. 96. 88. 11.  8. 74.]
 [67. 46. 46. 96. 88. 46.  8. 74. 62.]
 [18. 96. 88. 11.  8. 74. 54. 94. 18.]
 [96. 88. 46.  8. 74. 62. 94. 18. 46.]
 [70. 50. 69. 27. 14. 92.  7. 52. 36.]
 [50. 69. 49. 14. 92. 37. 52. 36. 88.]
 [27. 14. 92.  7. 52. 36. 71. 88.  7.]
 [14. 92. 37. 52. 36. 88. 88.  7. 13.]]
=============================

# im2colの処理（transposeしない場合）
============= col ==============
 [[45. 38. 10. 12. 38. 44. 12. 97. 44.]
 [41. 97. 33. 10. 12. 57. 30. 12. 97.]
 [30. 76. 97. 33. 76. 58. 57. 30. 67.]
 [95. 30. 76. 95. 30. 76. 58. 30. 53.]
 [54. 73. 63. 52. 73. 91. 52. 30. 91.]
 [ 1. 30. 79. 63. 52. 56.  1. 52. 30.]
 [ 1. 88. 30. 79. 88. 65. 56.  1. 29.]
 [33.  1. 88. 33. 97. 88. 65. 97. 32.]]
==============================

# ストライドが2の場合
============= col ==============
 [[54. 15. 90. 29. 97. 46. 53.  5. 16.]
 [55. 93. 14. 47. 16. 92. 62. 23.  2.]]
==============================

CNNの実行結果

正答率(トレーニング) = 0.9926
正答率(テスト) = 0.958

考察

• imageからcolumnに変換するイメージがついた
• ストライドやフィルターを変更した際の挙動を理解した
• mnistのデータは画像なので、CNNの学習が一番最適であることが再認識できた