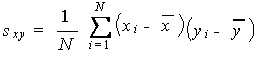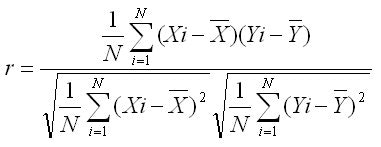初学者向けとして共分散と相関係数について勉強した上でプログラミングツール「R」を使って変数間の関係性を数学的に示します。
共分散って何?相関係数って何?
主に統計の初学者を対象に記事を書いてみました。
ちょっと前準備が必要ですが、以前にも初学者向けに分散と標準偏差、母集団・標本の考え方について記事を書きました。
そちらをお読みいただけたのでしたら十分理解することができる内容になっています。
すでにご理解がお済みでしたら前準備は不要です。
数字ばかりをにらめっこするのは筆者のような数学に苦手意識の強い人には堪えるので、今回は変数間の関係を視覚的に示す図表である「散布図」も表示してみます!
こんな方向けに書いてみました
- 共分散と相関係数って何を意味するのか知りたい
- 共分散と相関係数の違いって何?
- 仕事で必要になったので、思い出したい
- 学校で理解に追いつけなかったので、復習したい
- 統計の勉強をしていて、ステップアップしたい
必要なもの
- Rの開発環境ならびに基礎知識(変数とベクトル、関数の使い方程度で大丈夫です)
- 分散と標準偏差の算出方法を知っている ※1
- 母集団と標本の違いを知っている ※2
※1 分散と標準偏差についての記事はこちら
※2 母集団と標本についての記事はこちら
共分散と相関係数
共分散と相関係数ってなんなの?
ざっくり復習ですが、分散や標準偏差はひとつの変数を数式で計算し、その特徴を表すものでした。
実際の研究や実験では複数の変数を対象に、その関係性を明らかにして検討することがよく行われます。
なんとなくお察しいただけたかと思いますが、今回扱う共分散と相関係数は変数間の関係性を数字で表したものを意味しています。
そしてどうしても避けて通れないものに計算式があります。
さっと触れてあとは難しい考え方を持ち出さないようにしますので、まずは堪えるんだ。
**あぁ、うん。むーりぃ。**って思う方もいらっしゃるかもしれませんが、順を追って説明しますのでご安心を。
それから実際に多く使われる場面が多いのは相関係数だったりするのですが、その理由も後述します。
説明に入る前準備として、まずは変数とその関係とは何か?という点から説明します。
なお、今回は標本と母集団という概念をご理解いただけたという前提を踏まえて標本から関係性を算出・検討するということを意識してください。
変数とその関係について
プログラムに触れる方は変数という概念に慣れていることでしょうが、馴染みがない方はそうでもありません。
変数とは簡単に説明するとデータを入れておくための箱のようなものです。
そして統計で扱う変数には二種類あります。
ひとつは質的変数と呼ばれる変数です。
これはデータに優劣がなく、大小の比較ができないものを意味します。
例えば「性別」や「学問の好き嫌い」などが挙げられます。
男性と女性、好きと嫌いというデータは加減乗除ができず、大小の比較・検討はできないですよね。
もうひとつは量的変数と呼ばれる変数です。
これはデータに優劣があり、大小が存在するものです。
例えば「身長」や「体重」などが該当するでしょう。
いずれも大小があり、比率などを求めることがありますよね。
変数の正体が分かったところで、変数間の関係とはどういうことなのでしょうか。
質的変数で考えてみましょう。
一例として都内で勤務する社会人を対象に「甘党か辛党か」、「洋食派か和食派か」というアンケートをとった結果、甘党には和食派が多く辛党には洋食派が多いという傾向が見られました。このような変数間の関係を連関と言います。
量的変数の例も考えます。
大学生100名を対象に国語と数学のテストを実施しました。
結果、国語の点数が良い生徒は数学の点数が悪いという傾向が見られたとします。
このような関係は相関と呼ばれます。
今回は相関を検討するために共分散と相関係数を求めますが、変数の関係についてもう少し追ってみましょうか。
変数の関係をあらわす表現というものがあります。
2変数(xとy)あったとして、以下の3パターンです。
| 表現(xとyの関係) | 傾向例 |
|---|---|
| 正の相関 | 変数xが大きいとき、変数yも大きい傾向にある |
| 負の相関 | 変数xが大きいとき、変数yは小さい傾向にある |
| 無相関 | 変数xとyの大小の変化はない |
以上が準備運動です!
では共分散の求め方について勉強しましょう。
変数と関係のまとめ
- 変数とはデータを入れておくための箱のようなもの
- 質的変数:データに優劣がなく、大小の比較ができない変数
- 量的変数:データに優劣があり、大小が存在する変数
- 質的変数同士の関係を表すものを連関という
- 量的変数同士の関係を表すものを相関という
共分散ってどうやって求めるの?
準備運動が終わったところで共分散の求め方を学習します。
冒頭で述べた通り、共分散とは変数間の関係性を数字で表したものです。
冒頭の計算式はやたら難しいことが書いてありますがあわてず、これまで勉強してきたことを活かせば以下のように要約することができそうです。
共分散(Sxy): Σ(データx - データxの平均)(データy - データyの平均) /n -1
こんな感じでしょうか。
しっくり来なければ読み飛ばして構いませんが、雑な言い方をすると「変数間における平均からの偏差の積」を求めると共分散になるということです。
相関係数ってどうやって求めるの?
共分散と同じ要領で、相関係数の式も簡略化させてみましょう。
相関係数(r): 共分散 / xの標準偏差 * yの標準偏差
学んだことを分かりやすい形で数式に反映させることができれば難しいことはないのですが、親切にやり過ぎてしまうことで、かえって数学慣れしていない初学者の敷居を高くしてしまうのは皮肉なことだな…なんて筆者は思うことがあります。
さておき、相関係数で求められた結果は必ず±1の範囲になります。
相関係数で求められた結果に強い相関があったか、弱い相関があったかを測る明確な基準というものはありませんが、参考までに以下の表を示しておきます。
※他のサイトだと範囲と評価が異なることがあります。
相関係数の大きさの評価
| 相関係数 | 評価 |
|---|---|
| 〜 ± 0.2 | ほぼ無相関 |
| 〜 ± 0.4 | 弱い相関あり |
| 〜 ± 0.7 | 中程度の相関あり |
| 〜 ± 1.0 | 強い相関あり |
先に説明した通り、無相関係数は0に近くなり、負の相関が強くなれば-1に近づき、正の相関が強くなれば1に近づいていきます。
最後に、大事なことを説明しましょう。
前述の通り、共分散も相関係数も意味するものは同じです。
ですが一般によく使われるのは相関係数です。
その理由を説明します。以下のデータを見てください。
身長(cm)と体重(kg)のデータ
| 身長(cm) | 体重(kg) |
|---|---|
| 150 | 50 |
| 160 | 60 |
| 170 | 70 |
| 180 | 80 |
| 190 | 90 |
身長(m)と体重(kg)のデータ
| 身長(m) | 体重(kg) |
|---|---|
| 1.5 | 50 |
| 1.6 | 60 |
| 1.7 | 70 |
| 1.8 | 80 |
| 1.9 | 90 |
極端な例ですが、このようなデータがあったとしましょう。
身長の単位が異なるだけのデータです。
それぞれ共分散と相関係数を求めたらどうなるでしょうか。
やってみましょう。まずは共分散から。
共分散の算出結果:
身長(cm)と体重(kg)のデータ - (150-170)(50-70)+(160-170)(60-70)+(170-170)(70-70)+(180-170)(80-70)+(190-170)(90-70) / 5 - 1 = 250
身長(m)と体重(kg)のデータ - (1.5-140.3)(50-70)+(1.6-140.3)(60-70)+(1.7-140.3)(70-70)+(1.8-140.3)(80-70)+(1.9-140.3)(90-70) / 5 - 1 = 2.5
次に、共分散をもとに相関係数を算出します。
※標準偏差の計算式は省略して書いてあります。
相関係数の算出結果:
身長(cm)と体重(kg)のデータ - 250 / (15.81139 * 15.81139) = 1
身長(m)と体重(kg)のデータ - 2.5 / (0.1581139 * 15.81139) = 1
いかがでしょうか。
共分散では異なる結果となり、相関係数では同じ結果が得られました。
測定単位が変わろうが、変数が示す本質的な意味合いは同じのはずです。
にもかかわらず結果が変わってしまうのは問題ですよね。
つまり、相関係数がより利用されるのは、測定単位の影響を受けない指標だからなのです。
以上で共分散と相関係数の説明を終わります。
少し休憩して、Rでも同じことをやってみましょう。
共分散と相関係数のまとめ
-
共分散も相関係数も「変数間の関係性を数字で表したもの」を意味している
-
共分散(Sxy)は以下の式で算出することができる
Σ(データx - データxの平均)(データy - データyの平均) /n -1 -
相関係数(r)は以下の式で算出することができる
Sxy / xの標準偏差 * yの標準偏差 -
相関係数で求められた結果は必ず±1の範囲となる
-
共分散よりも相関係数がよく利用されるのは、測定単位の影響を受けない指標だから
Rで共分散と相関係数を求めてみよう
Rで共分散を求めてみよう
準備運動が終わったところでRで共分散を求めてみましょう。
今回は野球選手のデータをサンプルに使います。
こちらのリンクをクリックしてサンプルファイルをダウンロードしてください。
リンク先の「こちら」という文字をクリックするとダウンロードが開始されます。
使用するのは「baseball.txt」というファイルです。

ダウンロードが終わったらファイルを適当なディレクトリに配置してください。
個人的にはRのワークスペース付近がおすすめです。
ファイルを置いたら読み込みます。
# ワークスペース確認
getwd()
# ファイルが存在しているか確認 TRUE or FALSE
file.exists("Baseball.txt")
# ファイル読み込み
res <- read.delim("Baseball.txt",header = T)
getwd()関数はワークスペースを表示してくれる関数で、file.exists()は引数に指定したファイルが存在しているか(TRUE or FALSE)を返してくれる関数です。
read.delim()関数はタブ区切りのテキストファイルをベクトルとして読み込む場合に使う関数です。
第二引数は一行目のヘッダ(列名)の読み込みを有効にする場合に指定します。
準備が終わったら共分散を求めてみましょう。
Rには標準で共分散を算出してくれる関数**cov()**が用意されています。
ファイルの内容で相関がありそうな項目は何が考えられるでしょうか。
「Batting.Average(打率)」と「On.Base.Percentage(出塁率)」には相関がありそうな気がしませんか?
「ベクトル名 + $ + 列名」で特定の列名のみ抽出できるので、cov関数を使って結果を見てみましょう。
# ワークスペース確認
getwd()
# ファイルが存在しているか確認 TRUE or FALSE
file.exists("Baseball.txt")
# ファイル読み込み
res <- read.delim("Baseball.txt",header = T)
# 打率と出塁率の共分散を求める
# 「ベクトル名 + $ + 列名」で特定の列のみ抽出できる
cov(res$Batting.Average,res$On.Base.Percentage)
cov()関数を実行します。
> [1] 0.0006641195
共分散が算出されました。
同じように相関係数も算出してみましょう。
Rで相関係数を求めてみよう
Rで相関係数を算出します。
共分散と同じく、Rには相関係数を算出してくれる関数**cor()**が存在します。
やってみましょう。
…途中省略
# 打率と出塁率の相関係数を求める
cor(res$Batting.Average,res$On.Base.Percentage)
実行してみると結果は以下が表示されました。
0.7449227
約0.74だったとして、強い相関がありそうですね!
他の組み合わせも試して相関を確かめてみましょう。
…途中省略
# 打率と出塁率の相関係数を求める
cor(res$Batting.Average,res$On.Base.Percentage)
# ヒット数とホームラン数の相関係数を求める
cor(res$Hits,res$Home.Runs)
ヒット数とホームラン数の相関を調べてみます。
どうなるでしょうか。
> [1] 0.5444808
中程度の相関が見られる結果となりました。
調べてみると意外な相関が見られる例もあり、おもしろいので色々と試してみてください!
Rで散布図を描いてみよう
最後に、2変数の相関を視覚的に把握するという意味で散布図を描いてみましょう。
数字で表示するよりも感覚的にわかりやすく、「散布図はこうなっていて相関係数はこのぐらいです!」と要約するだけでも論文などを読む側としてはとても楽です。
Rでは散布図を表示させる関数**plot()**が標準で用意されています。
Rスゴイ!
…途中省略
# 打率と出塁率の散布図を表示させる
plot(res$Batting.Average,res$On.Base.Percentage)
では、表示させてみましょう。

散布図が表示されました。
他にも点に色を表示させたり、点が重なっている部分を工夫して見せたり、複数の散布図を並べて見せることができたりなど、広く応用を利かせることができます。
以上で共分散と相関係数の説明を終わります。
おわりに
これまでの記事で何度も書いてきたのですが、Rを使えば煩雑な処理を一気に解決出来ることが多い魅力的な言語です(GUIがしょっぱいのが玉に瑕ですが)。
気に入ったら学校で友達に自慢したり、職場で共有してみてください。
複数のデータを検討するということは統計の論文や研究に限った話ではなく、日常でもよく議論されていることでもあります。
例えば「離職率の高い会社って給料低いの?」とか「ゲームが好きな人ってアニメも好きなことが多いの?」とか、いかにもありそうなテーマじゃないですか。
データさえあればRで数学的に相関を出せちゃうので、気になることがあったら調べてみると良いでしょう。
今回までの記事でデータの特徴を一つの数字であらわす、いわゆる「記述統計」と呼ばれる統計の基本的な部分のお勉強は終了です。
次回は「推測統計」と呼ばれる統計の勉強をはじめたいのですが、その前に確率論について触れておかないとたぶんパンクするので、確率論のお話をしたいと思います。
それでは、お疲れ様でした。
ここまで読んでいただき、ありがとうございましたー!