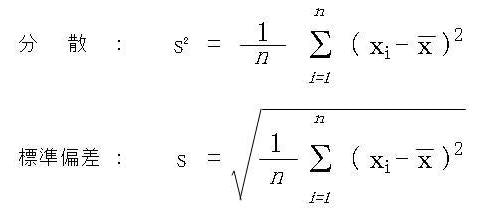【初学者向け】Rではじめる統計学 分散と標準偏差

はじめに

初学者向けとして統計（分散と標準偏差）のお勉強をした上で統計に特化したプログラミングツール「R」を使い簡単に分散と標準偏差を求めてみます。

このページでは極力記号文字を使わず、別のものに置き換えながら説明をしますので、全く統計と縁のない方でもご安心ください。

分散と標準偏差にはそれぞれ母分散と母標準偏差、標本分散と標本標準偏差がありますが、今回は母分散と母標準偏差を算出してみます。

こんな方向けに書いてみました

・Rには興味ないけど、分散と標準偏差の求め方を知りたい
・分散と標準偏差の勉強をしてみたけど、心が折れかけた
・仕事で必要になった
・Rの使い方はなんとなくわかったので、そろそろ統計っぽいことしてみたい
・ひまつぶし
・自分のための備忘録

※Rには興味ねーよ！って方は分散と標準偏差の説明だけお読みいただければと。

必要なもの

・Rの開発環境
・Rの基礎知識（変数とベクトル、関数の概念程度で大丈夫です）
・折れない心

筆者の開発環境

・MacOS X 10
・R -3.3.3
・RStudio -1.0.136

※OSや言語のバージョンは気にしなくても動作しますが、念のため。

分散と標準偏差

そもそも分散と標準偏差ってなんなの？

四則演算と平均は余裕でできるもんね！という方でも「分散」と「標準偏差」の領域に足を踏み入れた途端、「むーりぃ…」ってなる方はとても多いのではないでしょうか。
その原因は多分コレ。

分散と標準偏差の式です。
わかるかよ。

しかし、無理もありません。
見ていただいたモノは日常生活の中ではまず使わないものでしょうから。

そして初学者は誰もが思うことでしょう。
「まず記号の意味からわかりやすく説明しろよ」と。

例えるなら方程式がわからないのに連立方程式の学習から始めるような、そんな漠然とした不安を感じるはずです。

しかし、2つの式の結果が示すことはどちらも変わりありません。
どちらも「中心値（平均値）からのバラツキの大きさ」を示すものなのです。

分散ってどうやって求めるの？

概要を説明したところで分散の求め方について説明します。
その前に、分散も標準偏差も同じ意味を示すなら、その違いって何でしょう？という至極真っ当な疑問が思い浮かぶかもしれませんが、その疑問への回答は後述させてください。

まず、分散とは「中心値（平均値）からのバラツキの大きさ」を示すものだということを前に説明しました。
では例としてAくんとBくんの数学のテスト結果を見てどれぐらい平均からバラついているかを考え方を説明しながら進めていきます。

AくんとBくんの数学テストの結果(全6回)

Aくん	Bくん
68	88
89	78
78	65
82	59
77	79
66	91

上の表はA君とBくんの全6回の数学テストの結果です。
まずはそれぞれの平均点を求めてみましょう。これは簡単ですね。

Aくんの平均点　:　(68+89+78+82+77+66) / 6 = 76.66667(点）
Bくんの平均点　:　(88+78+65+59+79+91) / 6 = 76.66667(点）

それぞれの平均点はあえて同じにしてみました。
では平均点はどれぐらいバラついているかを見ましょう。
単純に考えれば得点から平均点を引いた値を合計すれば求められそうですね。

Σ(得点 - 平均点）

ここでΣ（シグマ）という見慣れない記号が登場しました。
これは**「全体の結果（和）を求めてくださいね」**っていう意味です。
他の統計学では大変よく出てくるので、覚えておきましょう。

得点から平均を引いた結果は以下のようになりました。

AくんとBくんのそれぞれの得点から平均(76.66667点)を引いた結果

Aくん	Bくん
-8.6666667	11.333333
12.3333333	1.333333
1.3333333	-11.666667
5.3333333	-17.666667
0.3333333	2.333333
-10.6666667	14.333333

では、合計してみましょう。
どうなるでしょうか。

Aくんの得点から平均を引いた結果の合計　:　(-8.6666667)+(12.3333333)+(1.3333333)+(5.3333333)+(0.3333333)+(-10.6666667) = -0.0000002

Bくんの得点から平均を引いた結果の合計　:　(11.333333)+(1.333333)+(-11.666667)+(-17.666667)+(2.333333)+(14.333333) = -0.0000002

結果は限りなく0に近い数値になってしまいました。得点と平均点を更新しても同じ結果が出るはずです。
プラスとマイナスの値が相殺してしまった影響によるものです。

しかし、これではどれだけバラついているのかわかりませんね。同じ値が出ちゃったし。
ではどうすれば良いでしょうか。

次に考えられるのは得点から平均を引いた値に二乗をすれば影響を受けずに済むということではないでしょうか。式にするとこんな感じですね。

Σ(得点 - 平均値)^2

二乗した結果の和を求めればなんかいけそうな気がしませんか？
やってみましょう。

AくんとBくんのそれぞれの得点から平均(76.66667点)を引いて二乗した結果

Aくん	Bくん
75.1111111	128.444444
152.1111111	1.777778
1.7777778	136.111111
28.4444444	312.111111
0.1111111	5.444444
113.7777778	205.444444

Aくんの得点から平均引いて二乗した合計：75.1111111+152.1111111+1.7777778+28.4444444+0.1111111+113.7777778=371.3333

Bくんの得点から平均引いて二乗した合計：128.444444+1.777778+136.111111+312.111111+5.444444+205.444444=789.3333

どえらい点数になりましたが、差を算出することができましたね。
B(789.33) > A(371.3333)でBくんがAくんよりばらつきが大きいということがわかりました。

しかし、この方法でばらつきを求めることには弱点があります。
それはサンプルサイズが増えれば増えるほど、値が大きくなるということです。
例を見てみましょう。

テストを受けまくるAくん

Aくん	Bくん
68	88
89	78
78	65
82	59
77	79
66	91
98
82
24
34
66

取り憑かれたかのようにテストを受けまくるAくん。
明らかに赤点を取るのもお構いなし。

計算式は割愛しますが、結果は A(4990.727) > B(789.33)となり、AくんがBくんよりばらつきが大きくなってしまいました。
このようにデータ数そのものが増えたりすると極端な差が開いてしまいます。
これを防ぐためには、

Σ(得点 - 平均点）^2 / n(データ数）

とすることで不平等な結果を避けることができます。
この算出結果として求めたものが分散です。

Aくんの分散：(68 - 69.45455)^2 +
(89 - 69.45455)^2 +
(78 - 69.45455)^2 +
(82 - 69.45455)^2 +
(77 - 69.45455)^2 +
(66 - 69.45455)^2 +
(98 - 69.45455)^2 +
(82 - 69.45455)^2 +
(24 - 69.45455)^2 +
(34 - 69.45455)^2 +
(66 - 69.45455)^2 /
11 = 453.7025

Bくんの分散：(88 - 76.66667)^2 +
(78 - 76.66667)^2 +
(65 - 76.66667)^2 +
(59 - 76.66667)^2 +
(79 - 76.66667)^2 +
(91 - 76.66667)^2/
6 = 131.5556

先ほどより極端な結果ではありませんが、A(453.7025) > B(131.5556)でAくんのばらつきが大きいという結果になりました。

分散のまとめ

• 分散は中心値（平均値）からのバラツキの大きさを示すものである
• Σ（シグマ）は全体の結果（和）を求めるための省略記号
• Σ(実際の値 - 平均)^2 / n(データの数）で算出できる
• （実際の値 - 平均）するとプラマイゼロになるので、バラツキを出すため、あえて二乗して計算している
• 分母にn(データ数）があるのは片方のデータ数が増えた時、極端な差を出さないための配慮

おつかれさまでした。
分散の説明は以上です。
少し休憩してから標準偏差の説明を読んでみてください。
　

標準偏差ってどうやって求めるの？

分散がわかってしまえば標準偏差はほとんど解けたようなものです。
次の式で解決することができます。

√分散

え、√ってなんだっけ…という方もいらっしゃるかもしれませんが、
簡単に説明しますと、√は二乗する前の数を意味します。
つまり、分散で求めた二乗する前の値ということです。

分散の説明時に登場したAくんとBくんの標準偏差を求めると次の結果になります。

Aくんの標準偏差：√453.7025 = 21.30029

Bくんの標準偏差：√131.5556 = 11.46977

標準偏差も分散と同じく中心値（平均値）からのバラツキの大きさを示すものだということは前に説明しましたが、一般には標準偏差が使われることが多いです。

その理由は扱う単位の問題にあります。
分散ではバラツキを求めるために、あえて二乗をしたので結果も「点数^2」となり、データを扱う側としては感覚的にはよくわかりませんよね。

だから√記号を使うことで、あえて二乗にした数値を前の状態に戻して「どれだけバラついているのか」をよりわかり易い形で算出しているのです。
これが分散と標準偏差を使い分ける理由です。

標準偏差のまとめ

• 分散と同じく、中心値（平均値）からのバラツキの大きさを示すものである
• √分散で標準偏差を算出することができる
• 分散で2乗して求めた結果を、2乗する前の数値に変換することで感覚的にわかりやすく扱うために標準偏差まで算出することが多い

Rで分散と標準偏差を求めてみよう

##Rで分散を求める

では実際にRで分散した結果を求めるために準備をしましょう。
データは分散の一番はじめに使った例のデータ(AくんとBくんの数学のテスト結果）にしましょう。適当にファイルをつくってください。

AくんとBくんの数学テストの結果(全6回)

Aくん	Bくん
68	88
89	78
78	65
82	59
77	79
66	91

分散の計算式もおさらいしておきましょう。
わからなくなったら分散のところの説明を読んでみてくださいね。

分散：Σ(実際の値 - 平均)^2 / n(データの数）

さて、準備はこんなところでしょうか。
では、RStudioを開いてデータを宣言するところからはじめましょうか。

Variance.R

#変数の宣言
data_A <- c(68,89,78,82,77,66)
data_B <- c(88,78,65,59,79,91)

次に、分散の計算式をプログラムに置き換えていきます。
今回は2人分のデータがありますので、同じ計算式を2人分用意するのは冗長です。
なので、関数をつくって呼び出すだけで分散の計算が行われるようにしてみましょう。

関数って何？という方は処理をひとまとめにしたものだと思ってください。
関数は一度つくってしまえば引数を渡すだけで呼び出すことができます。

Variance.R

#変数の宣言
data_A <- c(68,89,78,82,77,66)
data_B <- c(88,78,65,59,79,91)

#分散を計算する関数
Variance <- function(x){
  
  #平均値を求める
  mean_data <- mean(x)
  
  #データ数
  denominator_data <- length(x)
  
  #平均からの偏差
  deviation_from_standard <- x - mean_data 
  
  #平均からの偏差を二乗
  square_deviation_from_standard　<- deviation_from_standard^2
  
  #分散の計算
  variance <- sum(square_deviation_from_standard) / denominator_data
  variance
}

#関数を呼び出して分散を算出する
Variance(data_A)
Variance(data_B)

これで準備ができましたね。
関数の内部では以下の順で処理が行われます。

• 引数の平均値を算出する（mean()関数）
• 引数のデータ数を割り出す(length()関数)
• 各データの値から平均を引いたものを2乗する
• 分散の計算（Σ(実際の値 - 平均)^2 / n(データの数）)を実行する
• コンソールに分散の計算結果を表示させる

それでは「Variance(data_A)」と「Variance(data_B)」を実行してそれぞれ処理した結果を見てみましょう。
どうなるでしょうか。

　>Variance(data_A)
　[1] 61.88889
　>Variance(data_B)
　[1] 131.5556

分散を求めることができましたね。
では残りの標準偏差を求めてみましょう。

##Rで標準偏差を求める

Rで標準偏差を求めます。
標準偏差は次の式で求められるのでしたね。

標準偏差：√分散

分散と同じようにプログラムに置き換えてみましょう！

Variance.R

…省略

#変数に分散の結果を格納
sd_data_A <- Variance(data_A)
sd_data_B <- Variance(data_B)

#標準偏差
sqrt(sd_data_A)
sqrt(sd_data_B)

これだけです。
以下の順に処理が行われます。

• 分散を計算する関数の結果を変数に格納する
• 標準偏差を算出する（sqrt()関数により平方根に置き換えられる

結果を見てみましょう。

　>sqrt(sd_data_A)
　[1] 7.866949
　>sqrt(sd_data_B)
　[1] 11.46977

できましたね！
以上で標準偏差の説明は終わりです。

おわりに

いかがでしたでしょうか。
分散と標準偏差、むずかしいですよね。
筆者も駆け出しで、数時間おきにパソコンのモニタを粉砕してやりたくなる衝動に駆られます。

わかってしまえば簡単ですが、それでも手動で計算は面倒くさいですよね。
そんなとき、Rという言語をつかえばより簡単に、正確な結果を出すことができます。
むずかしい計算式でも、Rをつかえば簡単に計算してくれます。
ぜひ、使い方を覚えてみてください。

実は今回の分散と標準偏差についてですが、もっと簡単に割り出すことができます。
var()関数とsd()関数です。
ただし、この関数を実行すると今回得られた結果と近い結果が得られますが、異なる結果になります。

それには理由があって、不偏分散と不偏標準偏差という考え方のもとに計算されているためです(計算式はほとんど変わりないのでご安心を！)。
2つの違いに関してはまた次の機会があれば次回にてお話させてください。
次回までにパソコンのモニタが破壊されていなければ標準化についての説明をしようかな、と思ってます。

それでは、おつかれさまでしたー！