【初学者向け】Rではじめる統計学 母集団・標本と標準化

はじめに

初学者向けとして母集団・標本と標準化という考え方を勉強した上でプログラミングツール「R」を使って偏差値を算出します。

実は以前、「【初学者向け】Rではじめる統計学　分散と標準偏差」というタイトルで投稿させていただいたのですが、基本的な方針は前回と変わりません。
ふだん使わないような記号文字の使用は極力控えて説明します。
Rには興味ないけど計算方法だけ知りたい、という方も大歓迎です。

こんな方向けに書いてみました

• 標準化ってなんで求める必要があるのか知りたい
• 偏差値の算出方法を知りたい
• 仕事で必要になった
• 母集団・標本？標準化ってなんだったっけ？思い出したい

必要なもの

• Rの開発環境ならびに基礎知識(変数とベクトル、関数の使い方程度で大丈夫です）
• 分散と標準偏差の算出方法
• ネヴァーギブアップ精神

※分散と標準偏差ってなんだっけ？という方は以前に書いた記事をお読みいただくか、他のWEBぺージ等をご参考にしてください。
➡︎分散と標準偏差の記事はこちらからご参照いただけますよ!

母集団と標本

母集団と標本のちがいについて

標準化という概念に触れるためには標準偏差の算出方法は最低限知っておく必要があります。
そして標準偏差にも**「母標準偏差」と「不偏標準偏差」**といったものがあります。

さらに言えば多くの場面で不偏標準偏差が用いられるのですが、その理由を明らかにするために母集団と標本について例を出しながら説明をさせていただきます。

日本国民なら誰でも「チョコレートは『きのこの山』か『たけのこの里』か」というテーマについて、国内屈指の内戦が繰り広げられてきたのはご存知のことでしょう。
事あるごとに両派閥は激突し、アンケートの結果が開示されるたびに日本国民であるぼくらは一喜一憂し、勝者は凱旋の歌を歌い、敗者は血の涙をのんで盤面を覆す機会を虎視眈々と狙いながら、今日まで過ごしてきたわけです。

水を差すわけではありませんがアンケートの対象が日本国民全員だったとして、しかし文字通り日本国民全員にアンケートを実施することは現実的ではありませんよね。
呆れるほどのコストがかかってしまうことは明白です。
なのでアンケートを実施するのはあくまで日本国民の一部だったりするのが世の常です。

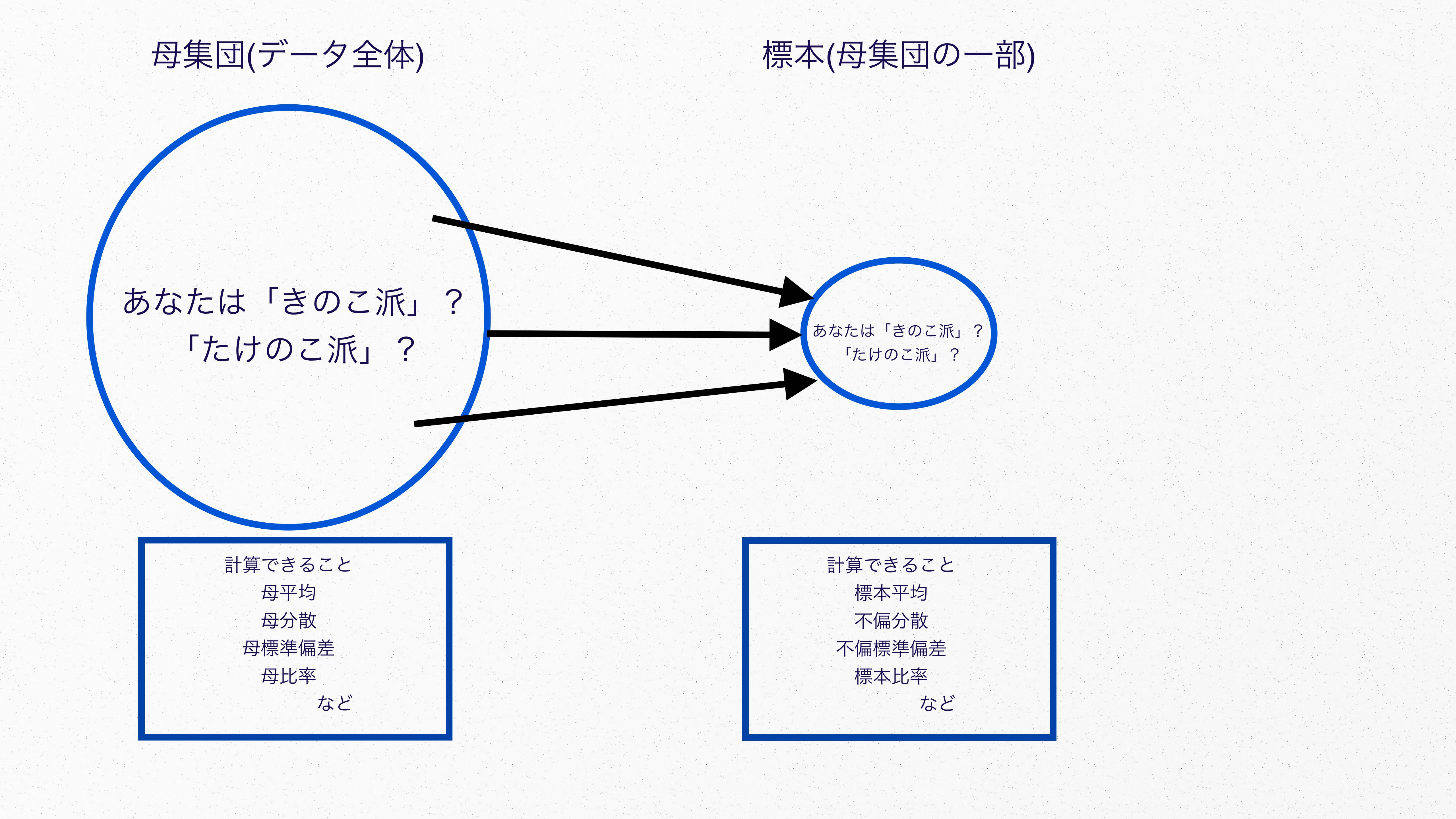
このように、関心のあるデータ全体を母集団と呼び、母集団の一部から抽出したデータ群を標本と呼びます。
なんとなくお察しいただけたかと思いますが、母集団と標本で算出した標準偏差をそれぞれ母標準偏差、不偏標準偏差と呼びます。

不偏標準偏差がより使われる理由は母集団という膨大なデータをもとに算出しているわけではなく、その一部を抽出した標本から算出しているケースが多いからなんですね。
標本から計算されるものは標本統計量と呼ばれます。

前回のおさらいですが、標準偏差は

Σ(X - Xの平均）^2 / n(データ数）

とすることにより求めることができると説明しました。
これは母標準偏差を求める式と同等なのですが、不偏標準偏差を求める場合は

Σ(X - Xの平均）^2 / (n(データ数）-1)

とすることで算出することができます。
違いは分母のデータ数から1を引いただけですね。

ここで「なんで n - 1 する必要があるの？」という疑問はもっともですが、調べてみたら準備が大変で豪快に脱線することが目に見えましたので、一旦は理解を先に進めることにします。

###母集団と標本のまとめ

• 対象のあるデータ全体を母集団と呼ぶ
• 母集団から抽出した一部のデータを標本と呼ぶ
• 標本から計算されるものを標本統計量と呼ぶ(不偏分散、不偏標準偏差など）
• 不偏標準偏差は「Σ(X - Xの平均）^2 / (n(データ数）-1)」により求められる

標準化

標準化という考え方

標準化について説明します。
標準化とは何かと言いますと、平均と標準偏差がある特定の値になるように、すべてのデータの値を計算式で変換することです。

次に、なぜ標準化をさせる必要があるのかを説明しますと、平均と標準偏差を特定の値に統一することで、データ間の比較・検討を容易にすることができるということです。
例を挙げて説明しましょう。

英語と数学のテスト結果

数学	英語
49	88
80	91
82	59
83	52
84	78
66	77
57	81
51	76
60	65
70	71

英語と数学のテスト結果をデータ化しました。
それぞれ異なるデータ群です。

しかし、これだけではデータがあるというだけで意味がありません。
平均と標準偏差も求めてみます。

せっかく勉強したので、今回からは不偏標準偏差を用いて計算をしていきましょうか。
以下の結果になりました。

数学と英語の平均と標準偏差

	平均	標準偏差
数学	68.2	13.59575
英語	73.8	12.29995

計算式は省略しますが、こんな感じになりました。
では情報が出揃ったところで、2つの情報を比較してくださいと言われたら、とっても困惑するでしょう。
それぞれの平均と標準偏差という前提が異なるからです。

そこで登場するのが標準化です。
平均と標準偏差をそれぞれ特定の値に変換することができればイーブンの関係が成立することができると思いませんか？

標準化の例として、平均を0、標準偏差を1に変換する方法がしばしば用いられます。
これをz得点といいます。
計算方法は、

z得点:得点 - 平均点 / 標準偏差

とすることにより算出できます。
やってみましょうか。

数学のz得点:49 - 68.2 / 13.59575 = -1.4122059
80 - 68.2 / 13.59575 = 0.8679182
82 - 68.2 / 13.59575 = 1.0150230
83 - 68.2 / 13.59575 = 1.0885754
84 - 68.2 / 13.59575 = 1.1621278
66 - 68.2 / 13.59575 = -0.1618153
57 - 68.2 / 13.59575 = -0.8237868
51 - 68.2 / 13.59575 = -1.2651011
60 - 68.2 / 13.59575 = -0.6031296
70 - 68.2 / 13.59575 = 0.1323943

英語のz得点:88 - 73.8 /12.29995 = 1.1544758
91 - 73.8 /12.29995 = 1.3983791
59 - 73.8 /12.29995 = -1.2032565
52 - 73.8 /12.29995 = -1.7723642
78 - 73.8 /12.29995 = 0.3414647
77 - 73.8 /12.29995 = 0.2601636
81 - 73.8 /12.29995 = 0.5853680
76 - 73.8 /12.29995 = 0.1788624
65 - 73.8 /12.29995 = -0.7154498
71 - 73.8 /12.29995 = -0.2276431

それぞれのz得点を算出することができました。
標準化の概要が理解できたら次のステップに進みましょう。

偏差値ってどうやって求めるの？

標準化の概念が理解できたところで、偏差値について学びましょう。
偏差値は標準化の手法のひとつで平均が50、標準偏差が10になるよう標準化した得点のことです。
算出方法は

偏差値:z得点*10+50

によって求めることができます。

数学の偏差値:-1.412205910+50 = 35.87794
0.867918210+50 = 58.67918
1.015023010+50 = 60.15023
1.088575410+50 = 60.88575
1.162127810+50 = 61.62128
-0.161815310+50 = 48.38185
-0.823786810+50 = 41.76213
-1.265101110+50 = 37.34899
-0.603129610+50 = 43.96870
0.132394310+50 = 51.32394

英語の偏差値:1.154475810+50 = 61.54476
1.398379110+50 = 63.98379
-1.203256510+50 = 37.96744
-1.772364210+50 = 32.27636
0.341464710+50 = 53.41465
0.260163610+50 = 52.60164
0.585368010+50 = 55.85368
0.178862410+50 = 51.78862
-0.715449810+50 = 42.84550
-0.227643110+50 = 47.72357

偏差値を求めることができましたね。

これで標準化の説明は終わりです。
でもほんとに平均値は50で標準偏差値は10になってるの？と気になる方もいらっしゃると思うので、Rの実行時に確認してみましょう。

標準化のまとめ

• 標準化とは、平均と標準偏差がある特定の値になるように、すべてのデータの値を計算式で変換することである

• 標準化を用いて平均と標準偏差を特定の値に統一することで、データ間の比較・検討を容易にすることができる

• z得点は平均が0、標準偏差が1になるよう標準化した得点を意味する
  ・z得点:得点 - 平均点 / 標準偏差

• 偏差値は平均が50、標準偏差が10になるよう標準化した得点を意味する
  ・偏差値:z得点*10+50

Rで偏差値を求めてみよう

勉強が終わったところでRを使って偏差値を算出してみましょう。
標準化の例で使ったデータを計算に使います。

英語と数学のテスト結果

数学	英語
49	88
80	91
82	59
83	52
84	78
66	77
57	81
51	76
60	65
70	71

まずは適当なファイルをつくって変数の宣言を行います。

Devian_Value.R

Mathematics <- c(49,80,82,83,84,66,57,51,60,70)
English     <- c(88,91,59,52,78,77,81,76,65,71) 

準備ができたら、z得点と偏差値を求める準備をしましょう。
以下の式で計算できるのでしたね。

z得点:得点 - 平均点 / 標準偏差

偏差値:z得点*10+50

プログラムに置き換えてみましょう!

Devian_Value.R

Mathematics <- c(49,80,82,83,84,66,57,51,60,70)
English     <- c(88,91,59,52,78,77,81,76,65,71) 

#z得点をそれぞれ算出
z_score_M < - (Mathematics - mean(Mathematics)) / sd(Mathematics)
z_score_E <-  (English - mean(English)) / sd(English)

#偏差値をそれぞれ算出
dv_M <- z_score_M*10+50
dv_E <- z_score_E*10+50

これで準備は完了です。偏差値はどうなったか見てみましょう。

　>dv_M
　[1] 35.87794 58.67918 60.15023 60.88575 61.62128 48.38185 41.76213 37.34899 43.96870
[10] 51.32394
　>dv_E
　[1] 61.54476 63.98379 37.96744 32.27636 53.41465 52.60164 55.85368 51.78862 42.84550
[10] 47.72357

無事算出できたようですね。
それでは平均が50で標準偏差が10になっているのか見てみましょう。

Devian_Value.R

…省略

#偏差値の平均
mean(dv_M)
mean(dv_E)

#偏差値の標準偏差
sd(dv_M)
sd(dv_E)

mean()関数は平均を算出でき、sd()関数は不偏標準偏差を算出します。
実行して確認してみましょう。

　>mean(dv_M)
　[1] 50
　>mean(dv_E)
　[1] 50
　>sd(dv_M)
　[1] 10
　>sd(dv_E)
　[1] 10

結果として平均は50、偏差値は10になることを確認できました。
Rだと確認がとても楽チンですね♫

このようにデータの結果が不揃いでも標準化することによってデータを比較・検討に用いることができます。
以上で標準化の説明は終わりです。

#終わりに

この記事を読んでいただきありがとうございました。
Rでは自動で計算してくれるので処理は早いですが、その前の標準偏差や標準化の理解でつまづいたという方は多いのではないでしょうか。筆者もその一人です。

それでも理解を深めていくとデータを扱って効果的に見せるということが楽しくなってくるので、Rと一緒に使ってみてください。
次は共分散と相関係数について展開し、より統計っぽいことができればなと考えています。
この記事が統計の初歩で苦しむ方への一助になれば幸いです。

おつかれさまでしたー