pythonで「入門 機械学習による異常検知」を読む5 時系列データの異常検知

「入門 機械学習による異常検知」はRで書かれた異常検知の本です。
今回は実装部分をpythonで書き直していこうと思います。

個人的な勉強のメモ書きとなります。
1章当たりのボリュームが多く、数式もかなりあるためうまくまとまっていません。
また、schikit-learnなどで関数が提供されていれば使っています。
導出や詳細などは「入門 機械学習による異常検知」を読んでいただければと思います。

前回
入力と出力があるデータからの異常検知

1. 近傍法による異常検知

スライド窓による時系列データの変換

1次元の時系列を考える。観測値として長さ$T$の時系列が$D={\xi^{(1)},\xi^{(2)},\cdots,\xi^{(T)}}$のように与えられたとする。
$w$個の隣接した観測値をまとめて

\boldsymbol{x}^{(1)}=
\left(\begin{array}{c}
\xi^{(1)}\\
\xi^{(2)}\\
\vdots\\
\xi^{(w)}
\end{array}\right),\ 
\boldsymbol{x}^{(2)}=
\left(\begin{array}{c}
\xi^{(2)}\\
\xi^{(3)}\\
\vdots\\
\xi^{(w+1)}
\end{array}\right),\ \cdots

のように、データを$w$次元ベクトルの集まりとして表すこととする。
長さ$T$の観測値からなる時系列データは
$$
N=T-w+1
$$
本の$w$次元ベクトルに変換される。
長さ$w$の窓を左から右に動かして、つぎつぎに長さ$w$の時系列片をつくっていく。この窓のことをスライド窓と呼ぶ。
スライド窓により生成したベクトルのことを、部分時系列と呼ぶことがある。

異常部位検出問題

ある程度滑らかな実数時系列データの場合、隣り合った部分時系列の要素の値はほとんど等しくなり、これを自己一致や自明な一致などと呼ぶ。

手順(異常部位発見)
訓練用の時系列$D_{tr}$と、検証用の時系列$D$を用意し、
それぞれを窓幅$w$により、部分時系列ベクトルの集合に変換しておく。
距離を計算するための関数distを用意する。異常度の判定に使う近傍数$k$を決めておく。
また、$k$近傍から異常度を計算する関数scoreを用意する。

1. $D$各要素$\boldsymbol{x}^{(t)}$について以下を行う($t=1,\cdots,N$)
   　a.距離の計算：distを用いて$D_{tr}$の各要素と$\boldsymbol{x}^{(t)}$の距離を計算する
   　b.スコアの計算：上記で求めた距離のうち最小のもの$k$個を選びscore関数により異常度を計算し記憶する
2. 異常度が最大のものを異常部位として列挙する

distについては、典型的にはユークリッド距離、ときにマハラノビス距離は使われるが、pノルムを使うこともできる。
類似度も使うことができ、最もよく使われるのが動的時間伸縮法による類似度である。
scoreに関しては、$k=1$と選んだうえで、最近傍までの距離の値そのものを異常度とすることが多い。
形式的に書くと次の通りである。
$$
scpre(\boldsymbol{x}^{(t)},D_{tr})=(\boldsymbol{x}^{(t)}の最近傍までの距離)
$$
$k>1$として平均値を考えることもできる。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

data = pd.read_csv('qtdbsel102.txt', sep='\t').reset_index()
data = np.array(data)

plt.figure(figsize=(10,5))
plt.plot(np.arange(3000),data[:3000,2])
plt.plot(np.arange(3000,6000), data[3000:6000,2])

from scipy.spatial.distance import cdist

w = 100 # 窓幅
nk = 1 # 近傍点

# 訓練用
Xtr = data[:3000,2] 
# 窓幅ずつ切り出していく
Dtr = np.array([Xtr[i:i+w] for i in range(3001-w)])

# テスト用
X = data[3000:6000,2]
# 窓幅ずつ切り出していく
D = np.array([X[i:i+w] for i in range(3001-w)])

# 距離の計算
D_dist = cdist(D, Dtr, metric='euclidean')

# 異常度の計算
# 近傍点との距離
a = np.min(D_dist, axis=1)

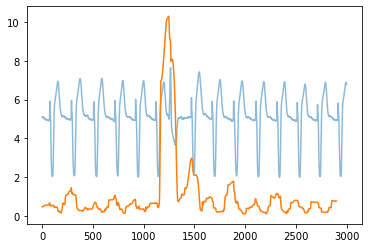
plt.plot(data[3000:6000,2], alpha=.5)
plt.plot(a)

2. 特異スペクトル変換法

前節での手法では、時系列に含まれるノイズが近傍の計算に多大な影響を与えるため誤検出などが起きる。
ノイズえお除去するために、ここでは部分空間法を用いた手法を説明する。

変化度の定義

カーネル主成分分析における変化解析問題において導入した式とまったく同様に、ここでも行列2ノルムを使って
$$
\begin{align}
a(t)&=1-|U_m^{(t)T}Q_m^{(t)}|_2^2\
&=1-\bigl(U_m^{(t)T}Q_m^{(t)}の最大特異値 \bigr)^2
\end{align}
$$
と定義することができる。
履歴行列$X_1^{(t)}$は、$\xi^{(t-k-w+1)}$から$\xi^{(t-1)}$までのデータを含むので、$t-k-w+1=1$を満たす時刻より過去側では計算はできない。
したがって$t=k+w$が変化度の計算の始まりとなる。
履歴行列$X_2^{(t)}$は、$\xi^{(t-k+L-w+1)}$から$\xi^{(t+L-1)}$までのデータを含むので、$t+L-1=T$を満たす時刻より$t$を超えるとテスト行列が構成できなくなる。
したがって$t=T-L+1$が変化度の計算の終わりとなる。
手順2(特異スペクトル変換)　時刻$D={\xi^{(1)},\xi^{(2)},\cdots,\xi^{(T)}}$を用意する。窓幅$w$、履歴行列の列サイズ$k$、ラグ$L$、パターン数$m$を決める。

1. $t=(w+k),\cdots,(T-L+1)$においてつぎの計算を行う。
   　a.(履歴行列とテスト行列)：$H_1^{(t)}$と$H_2^{(t)}$をつくる。($X_1^{(t)},X_2^{(t)}$の式)
   これは、時刻$t$の周りに、過去側と現在側において、$k$本の部分時系列を使った行列である。

X_1^{(t)}=[\boldsymbol{x}^{(t-k-w+1)},\cdots,\boldsymbol{x}^{(t-w-1)},\boldsymbol{x}^{(t-w)}]\\
X_2^{(t)}=[\boldsymbol{x}^{(t-k+L-w+1)},\cdots,\boldsymbol{x}^{(t-w-1)},\boldsymbol{x}^{(t-w+L)}]

それぞれの列ベクトルは長さ$w$の部分時系列である。
　b.(特異値分解)：$H_1^{(t)},H_2^{(t)}$を特異値分解し、左特異ベクトルの行列$U_m^{(t)},Q_m^{(t)}$を求める
　c.(スコアの計算)：$U_m^{(t)T}Q_m^{(t)}$の最大特異値を計算し、変化度$a(t)$を計算する

xi = data[3000:6001, 2]
w = 50 # 窓幅
m = 2 # パターン数
k = int(w/2) # 履歴行列の列サイズ 25
L = int(k/2) # ラグ 12
Tt = len(xi) # 3000

# 順番にスコアの計算を行う
score = np.zeros(Tt)
for t in np.arange(w+k, Tt-L+1): # 75 ~ 2989
    # 履歴行列を作る
    tstart = t-w-k # 始点
    tend = t-1 # 終点

    x1 = xi[tstart:tend] # データの取り出し
    X1 = np.array([x1[i:(i+w)] for i in range(len(x1)-w)]).T # 窓幅ごとに切り出す
    X1 = X1[::-1,:]
    
    # テスト行列を作る
    # 履歴行列のLだけ後のデータ
    tstart = t-w-k+L # 始点
    tend = t-1+L # 終点
    
    x2 = xi[tstart:tend] # データの取り出し
    X2 = np.array([x2[i:(i+w)] for i in range(len(x2)-w)]).T # 窓幅ごとに切り出す
    X2 = X2[::-1,:]
    
    # 特異値分解
    U = np.linalg.svd(X1)[0][:,:m]
    Q = np.linalg.svd(X2)[0][:,:m]
    
    # UQの特異値分解
    sig = np.linalg.svd(U.T@Q)[1][0]
    
    # スコアの計算
    score[int(t)] = 1 - sig**2

plt.plot(data[3000:6000,2]*0.0002, alpha=.5)
plt.plot(score)

# データの作成
x1 = np.arange(0,10,0.1)
x2 = np.arange(10,20,0.1)
x3 = np.arange(20,30,0.1)

# y2部分で周波数が異なるデータ
y1 = np.sin(np.pi*x1) + np.random.normal(len(x1), scale=0.07)
y2 = np.sin(2*np.pi*x2) + np.random.normal(len(x2), scale=0.07)
y3 = np.sin(np.pi*x3) + np.random.normal(len(x3), scale=0.07)
xi = np.concatenate([y1, y2,y3])

# 各パラメータ
w = 10
m = 2
k = 10
L = 5
Tt = len(xi)

score = np.zeros(Tt)
for t in np.arange(w+k, Tt-L+1):
    tstart = t-w-k
    tend = t-1
    x1 = xi[tstart:tend]
    X1 = np.array([x1[i:(i+w)] for i in range(len(x1)-w)]).T
    X1 = X1[::-1,:]
    
    tstart = t-w-k+L
    tend = t-1+L
    x2 = xi[tstart:tend]
    X2 = np.array([x2[i:(i+w)] for i in range(len(x2)-w)]).T
    X2 = X2[::-1,:]
    
    U = np.linalg.svd(X1)[0][:,:m]
    Q = np.linalg.svd(X2)[0][:,:m]
    sig = np.linalg.svd(U.T@Q)[1][0]
    score[int(t)] = 1 - sig**2

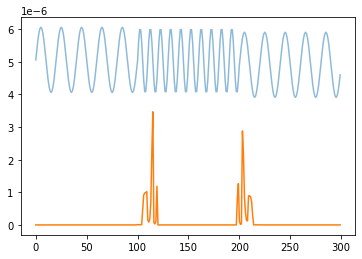
plt.plot((xi-95)*10**(-6), alpha=.5)
plt.plot(score)

3. 自己回帰モデルによる異常検知

いまの観測値$\xi^{(t)}$が、前の数個(例えば$r$個)の観測値の一次結合
$$
\xi^{(t)}\approx \alpha_1\xi^{(t-r)}+\alpha_2\xi^{(t-r+1)}+\cdots+\alpha_{r-1}\xi^{(t-2)}+\alpha_{r}\xi^{(t-1)}
$$
と考えるのが、次数$r$の自己回帰モデルである。

ベクトル自己回帰モデル

時刻$t$での観測値が、$M$次元ベクトル$\boldsymbol{\xi}^{(t)}$だとした自己回帰モデル
$$
\boldsymbol{\xi}^{(t)}\approx A_1\boldsymbol{\xi}^{(t-r)}+A_2\boldsymbol{\xi}^{(t-r+1)}+\cdots+A_{r-1}\boldsymbol{\xi}^{(t-2)}+A_{r}\boldsymbol{\xi}^{(t-1)}
$$
を考える。この場合、回帰係数に当たるものは$M×M$行列となる。
次の量を定義する。
$$
A=[A_1,\cdots,A_r],\ \boldsymbol{x}^{(t)}=
\left(\begin{array}{c}
\boldsymbol{\xi}^{(t)}\
\boldsymbol{\xi}^{(t+1)}\
\vdots\
\boldsymbol{\xi}^{(t+r-1)}
\end{array}\right),\
\boldsymbol{y}^{(t)}=\boldsymbol{\xi}^{(t+r)}
$$
$A$は$M×M$の係数行列で、$\boldsymbol{x}^{(t)}$は$rM$次元の長いベクトルである。
問題は、データ
$$
D={(\boldsymbol{x}^{(1)},\boldsymbol{y}^{(1)}),\cdots,(\boldsymbol{x}^{(N)},\boldsymbol{y}^{(N)}) }
$$
を基に、自己回帰モデル$\boldsymbol{y}^{(t)}\approx A\boldsymbol{x}^{(t)}$の係数行列$A$を推定する問題となる($N=T-r$)。
このモデルを次数$r$のベクトル自己回帰モデルと呼ぶ。

実行例

外れ値検出の問題であれば、ホテリング理論を流用して次のように定義する。
$$
a_{M=1}(\xi^{(t)})=\frac{1}{\hat{\sigma}^2}\biggl[\xi^{(t)}-\sum_{l=1}^r\hat{\alpha}_l\xi^{(t-l)} \biggr]^2\
a_M(\boldsymbol{\xi}^{(t)})=(\boldsymbol{\xi}^{(t)}-\hat{A}\boldsymbol{x}^{(t-r)})^T\hat{\Sigma}^{-1}(\boldsymbol{\xi}^{(t)}-\hat{A}\boldsymbol{x}^{(t-r)})
$$
ここで$\boldsymbol{x}^{(t-r)}$は$\boldsymbol{\xi}^{(t-r)}$から$\boldsymbol{\xi}^{(t-1)}$までを縦に並べたベクトルである。

手順(自己回帰モデルによる異常検知)
訓練用の時系列$D_{tr}$と、テスト用の時系列$D$を用意する。
データを観察して次数$r$の候補$r_1,r_2,\cdots$を決める。

1. モデルの推定：次数候補$r_1,r_2,\cdots$について以下を行い、AIC最小のモデルと、対応するモデルパラメータを求める。
   　a.　データの準備：$D_{tr}$を、回帰問題のデータに変換する
   　b.　最尤推定：$M=1$の場合は「1変数の自己回帰モデル」の式を使い、

L(\boldsymbol{\alpha},\sigma^2)=-\frac{N}{2}\ln(2\pi\sigma^2)-\frac{1}{2\sigma^2}\sum_{n=1}^N\bigl[y^{(n)}-\boldsymbol{\alpha}^T\boldsymbol{x}^{(n)} \bigr]^2\\
\hat{\boldsymbol{\alpha}}=[XX^T]^{-1}X\boldsymbol{y}_N\\
\hat{\sigma}^2=\frac{1}{N}\sum_{n=1}^N\bigl[y^{(n)}-\boldsymbol{\alpha}^T\boldsymbol{x}^{(n)} \bigr]^2

　　$M>1$の場合は「ベクトル自己回帰モデル」の式を使って未知パラメータを求め、

L(A,\Sigma|D)=-\frac{MN}{2}\ln(2\pi)-\frac{N}{2}\ln|\Sigma|-\frac{1}{2}Tr\biggl[\Sigma^{-1}(Y-AX)(Y-AX)^T \biggr]\\
\hat{\Sigma}=\frac{1}{N}(Y-\hat{A}X)(Y-\hat{A}X)^T\\
\hat{A}=YX^T(XX^T)^{-1}

記憶する
　c.　AICの計算：AICを求め、記憶する

AIC = -2L+2M_k=N\{M\ln(2\pi)+\ln|\hat{\Sigma}|+M\}+M(M+1)+2rM^2

　ここで、$M_k$は次数であり、今回は$rM^2+M(M+1)/2$となる。
　通常の自己回帰では$M=1$を考える。

1. 異常検知：$D$に含まれる$\boldsymbol{\xi}^{(1)},\boldsymbol{\xi}^{(2)},\cdots$に対して以下を行う
   　a.　異常度の計算：異常度の計算を行う
   　b.　異常判定：異常度が閾値を超えたら異常と判定する

from statsmodels.tsa import ar_model

nottem = pd.read_csv('nottem.csv').reset_index()
nottem = np.array(nottem)[:,1]
plt.plot(nottem)

# データの分割
Dtr = nottem[:120] # 訓練用
xi = nottem[120:] # テスト用
Tt = len(xi)

# 中心化
xmean = np.mean(Dtr)
Dtr_center = Dtr - xmean

aic = []
# 最適なラグを探索
# AICで評価
for i in range(20):
    maxlag = i
    model = ar_model.AutoReg(Dtr_center, lags=maxlag, trend='n', old_names=True)
    results = model.fit()
    aic.append(results.aic)

# AICが低いモデルを作成
r = np.argmin(aic)
model = ar_model.AutoReg(Dtr_center, lags=r, trend='n', old_names=True)
results = model.fit()

# 係数を取得
alpha = results.params

# σ2を取得
sig2 = results.sigma2

# テスト
# 中心化
xi_center = xi - xmean

# 切っていされた「ラグ」ずつデータを切り出す
X = np.array([xi_center[i:(i+r)] for i in range(len(xi_center)-r)])
X = X[:,::-1]

# 予測値の計算
pred = X@alpha+xmean

# 異常度の計算
a = (xi[r:] - pred)**2 / sig2

plt.figure(figsize=(8,4))
plt.plot((xi[r:]-10)*0.2)
plt.plot(a)

もう一つれを示す。
前の正弦波のようなデータではうまく検出できるが、
心電図のような変化が急なデータではうまく検出できない。

data = pd.read_csv('qtdbsel102.txt', sep='\t').reset_index()
data = np.array(data)

# データの分割
Dtr = data[:3000, 2]
xi = data[3000:6001, 2]
Tt = len(xi)

# 中心化
xmean = np.mean(Dtr)
Dtr_center = Dtr - xmean

aic = []
# 最適なラグを探索
# AICで評価
for i in range(20):
    maxlag = i
    model = ar_model.AutoReg(Dtr_center, lags=maxlag, trend='n', old_names=True)
    results = model.fit()
    aic.append(results.aic)

# AICが低いモデルを作成
r = np.argmin(aic)
model = ar_model.AutoReg(Dtr_center, lags=r, trend='n', old_names=True)
results = model.fit()

# 係数を取得
alpha = results.params

# σ2を取得
sig2 = results.sigma2

# テスト
# 中心化
xi_center = xi - xmean

# 切っていされた「ラグ」ずつデータを切り出す
X = np.array([xi_center[i:(i+r)] for i in range(len(xi_center)-r)])
X = X[:,::-1]

# 予測値の計算
pred = X@alpha+xmean

# 異常度の計算
a = (xi[r:] - pred)**2 / sig2

plt.figure(figsize=(8,4))
plt.plot((xi[r:]+1)*30)
plt.plot(a)

4. 状態空間モデルによる異常検知

線形状態空間モデル

時刻$t$における系の内部状態を$\boldsymbol{z}^{(t)}$という$m$次元ベクトルで表し、観測される量を$\boldsymbol{x}^{(t)}$という$M$次元ベクトルで表す。
線形状態空間モデルとは
$$
\boldsymbol{x}^{(t)}\approx C\boldsymbol{z}^{(t)}\
\boldsymbol{z}^{(t)}\approx A\boldsymbol{z}^{(t-1)}
$$
という式が成り立つと考えるモデルである。ここで$A$は$m×m$行列、$C$は$M×n$行列である。
$\boldsymbol{z}^{(t)}$は直接観測できないと想定されるので、潜在変数とも呼ばれる。
多くの場合、内部状態の遷移と、内部状態からの観測量への変換は正規分布に従って確率的に行われると仮定される。
$$
p(\boldsymbol{x}^{(t)}|\boldsymbol{z}^{(t)})=N(\boldsymbol{x}^{(t)}|C\boldsymbol{z}^{(t)},R)\
p(\boldsymbol{z}^{(t)}|\boldsymbol{z}^{(t-1)})=N(\boldsymbol{z}^{(t)}|A\boldsymbol{z}^{(t-1)},Q)
$$
がモデルとなる。
ここで、$Q$は内部状態の遷移のばらつきを表す$m×m$の共分散行列で、$R$は観測量のばらつきを表す$M×M$の共分散行列である。
始点の$t=1$に対応するため、上記に加えて
$$
p(\boldsymbol{z}^{(1)})=N(\boldsymbol{z}^{(1)}|\boldsymbol{z}_0,Q_0)
$$
を仮定しておく。
解くべき問題は2つあり、

• 観測データが得られたときに、状態変数の系列${\boldsymbol{z}^{(1)},\cdots,\boldsymbol{z}^{(t)}}$を推定すること
• 未知パラメータ$A,C,Q,R$を、データ$D$および状態変数系列から推定すること

である。

部分空間同定法

手順(部分空間同定法)
長さ$T$の$M$次元時系列$D$が与えられている。
窓$w$と部分時系列の数$N$を、$N\gg Mw$となるように選ぶ。時系列のおおむね中間地点を適当に選びそこを時刻$t$と見なす。

1. 状態系列の推定：窓幅$w$で時系列を切り取り、行列$X_p,X_f$を作る。

X_p=[\boldsymbol{X}^{(t-N)},\cdots,\boldsymbol{X}^{(t-2)},\boldsymbol{X}^{(t-1)}]\\
X_f=[\boldsymbol{X}^{(t)},\boldsymbol{X}^{(t+1)},\cdots,\boldsymbol{X}^{(t+N-1)}]

　a. $S_{pf},S_{pp},S_{fp}$をつくる

S_{pf}=X_pX_f^T\\
S_{pp}=X_pX_p^T\\
S_{fp}=X_fX_p^T

　b. $W$をつくり、特異値が大きい順に$m$本ほ特異ベクトルを求める

W=S_{pp}^{-1/2}S_{pf}S_{ff}^{-1/2}

　c. 左右の特異ベクトルから、$\hat{Z}_p$および$\hat{Z}_f$を求める。
　　左特異ベクトルを特異値の大きい順$\tilde{\boldsymbol{\alpha}}^1,\cdots,\tilde{\boldsymbol{\alpha}}^m$、右特異ベクトルを$\tilde{\boldsymbol{\beta}}^1,\cdots,\tilde{\boldsymbol{\beta}}^m$としたとき、

\boldsymbol{\alpha}^i=S_{pp}^{-1/2}\tilde{\boldsymbol{\alpha}}^i\\
\boldsymbol{\beta}^i=S_{ff}^{-1/2}\tilde{\boldsymbol{\beta}}^i

\hat{Z}_p=[\boldsymbol{\alpha}^1,\cdots,\boldsymbol{\alpha}^m]^TX_p\\
\hat{Z}_f=[\boldsymbol{\beta}^1,\cdots,\boldsymbol{\beta}^m]^TX_f

1. パラメータ行列の推定：観測値からなるデータ$D'={\boldsymbol{x}^{(1)},\cdots,\boldsymbol{x}^{(T')}}$と、先に状態推定の推定値$Z'={\hat{\boldsymbol{z}}^{(1)},\cdots,\hat{\boldsymbol{z}}^{(T')} }$を用意す($T'=T-w$)
   　a. データ行列$X,Z,Z_+,Z_-$を求める

X=[\boldsymbol{x}^{(1)},\cdots,\boldsymbol{x}^{(T-w)}]\\
Z=[\boldsymbol{z}^{(1)},\cdots,\boldsymbol{z}^{(T-w)}]\\
Z_+=[\boldsymbol{z}^{(2)},\cdots,\boldsymbol{z}^{(T-w)}]\\
Z_-=[\boldsymbol{z}^{(1)},\cdots,\boldsymbol{z}^{(T-w-1)}]

　b. $\hat{A},\hat{C},\hat{Q}\hat{R}$を求める

\hat{A}=(Z_+Z_-^T)(Z_-Z_-^T)^{-1}\\
\hat{C}=(XZ^T)(ZZ^T)^{-1}\\
\hat{Q}=\frac{1}{T'-1}(Z_+-\hat{A}Z_-)(Z_+-\hat{A}Z_-)^T\\
\hat{R}=\frac{1}{T'}(X-\hat{C}Z)(X-\hat{C}Z)^T

状態系列の逐次推定法：カルマンフィルタ

手順(カルマンフィルタ)
モデルパラメータ$A,C,Q,R,Q_0,\boldsymbol{z}_0$を与える。
$\boldsymbol{\mu}_0$を$A\boldsymbol{\mu}_0=\boldsymbol{z}_0$による定義する。
$t=1,\cdots,T$に対して次の計算を繰り返す。

K_t=Q_{t-1}C^T(R+CQ_{t-1}C^T)^{-1}\\
\boldsymbol{\mu}_t=A\boldsymbol{\mu}_{t-1}+K_t(\boldsymbol{x}^{(t)}-CA\boldsymbol{\mu}_{t-1})\\
V_t=(C^TR^{-1}C+Q_{t-1}^{-1})^{-1}\\
Q_{t-1}=Q+AV_{t-1}A^T

状態空間モデルを用いた異常検知

手順(状態空間モデルによる異常検知)
時系列データを用意し、訓練用データ$D_{tr}$と検証用$D$に分ける

1. パラメータの学習：$D_{tr}$を基に、部分空間同定法などの手段で、モデルパラメータ$A,C,Q,R,Q_0,\boldsymbol{z}_0$を求める
2. 異常度の逐次計算：$D$に含まれる観測値$\boldsymbol{x}^{(t)}(t=1,\cdots,T)$について、以下の手順で逐次異常度を計算する
   　a. カルマンフィルタの実行：カルマンフィルタを実行し、$\boldsymbol{\mu}{t-1}$と$Q{t-1}$を求める
   　b. 異常度の計算：異常度$a(\boldsymbol{x}^{(t)})$を計算し記憶する

a(\boldsymbol{x}^{(t)})=(\boldsymbol{x}^{(t)}-CA\boldsymbol{\mu}_{t-1})^T\Sigma_t^{-1}(\boldsymbol{x}^{(t)}-CA\boldsymbol{\mu}_{t-1})\\
\Sigma=R+CQ_{t-1}C^T

data = pd.read_csv('qtdbsel102.txt', sep='\t').reset_index()
data = np.array(data)

# データの分割
D = data[:6000,2]
Dtr = D[:3000]
T = len(D)

# 部分空間同定法：状態系列の推定
w = 5 # 窓幅
N = 1400 # 部分時系列の数

# 窓幅ずつデータを切り出す
x = np.array([Dtr[i:(i+w)] for i in range(len(Dtr)-w+1)]).T

# 行列XpとXfの作成
Xp = x[:,:N]
Xf = x[:,N:N*2]

# 分散行列・共分散行列の計算
Spf = Xp@Xf.T
Spp = Xp@Xp.T
Sff = Xf@Xf.T

# Wの作成
W = Spp**(-1/2)@Spf@Sff**(-1/2)
# Wの固有値分解
alpha = np.linalg.svd(W)[0]
beta = np.linalg.svd(W)[2].T
alpha = Spp**(-1/2)@alpha[:,0]
beta = Sff**(-1/2)@beta[:,0]

# 状態変数の系列の推定値
Zp = alpha.T@Xp
Zf = beta.T@Xf
z = np.concatenate([Zp,Zf])

# 部分空間同定法：未知パラメータ 𝐴,𝐶,𝑄,𝑅 の推定
# 観測行列と状態行列からなる行列
X = Dtr[:N*2-w]
Z = z[:N*2-w]

Z_p = z[1:N*2-w+1]
Z_m = z[:N*2-w]

# 𝐴,𝐶,𝑄,𝑅を計算する
A = (Z_p@Z_m.T)*(Z_m@Z_m.T)**(-1)
Q = 1/(len(Z)-1) * (Z_p - A*Z_m)@(Z_p - A*Z_m).T
C = (X@Z.T)*((Z@Z.T)**(-1))
R = 1/len(Z)*(X-C*Z)@(X-C*Z).T

# カルマンフィルタ
# 𝐴,𝐶,𝑄,𝑅(計算済み)以外のパラメータを与える
Q0 = 0.01
z0 = -1

# データの初期化
Kt = np.zeros(T) # カルマンゲイン
mut = np.zeros(T) # 平均
Vt = np.zeros(T) # 分散
Qt = np.zeros(T)
Qt[0] = Q0
mut[0] = z0/A

# カルマンフィルタの実行
# 各tのデータは保存しておく
for t in np.arange(1,T):
    Kt[t] = Qt[t-1]*C.T*(R+C*Qt[t-1]*C)**(-1)
    mut[t] = A*mut[t-1]+Kt[t]*(D[t]-C*A*mut[t-1])
    Vt[t] = (1-Kt[t]*C)*Qt[t-1]
    Qt[t] = Q + A*Vt[t]*A

# 分散行列の計算
Sig = R + C*Qt*C

# 異常度の計算
a = (D - C*A*mut)/Sig*(D - C*A*mut)

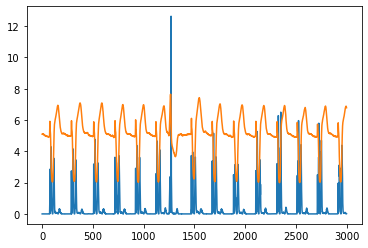
plt.plot(a[3000:])
plt.plot(D[3000:])

状態空間モデルとしては、statsmodelsのUnobservedComponentsなどが利用される。
ほぼ同様の結果が得られた。

import statsmodels.api as sm

model = sm.tsa.UnobservedComponents(D, 'local linear trend')
result = model.fit()

plt.plot(D[3000:]*0.1)
plt.plot((D-result.predict(1,6000))[3000:]**2)

これで「入門 機械学習による異常検知」は終了となります。
内容が自分には難しくうまくまとめられませんでした。

参考文献