はじめに
ちょうど1年前の12月8日にOpenCVでオセロ盤の盤面を認識するという記事を投稿しました。その記事では実際のオセロ盤を認識したのですが、今回はそのオセロ書籍版です。
発端となったのは2019年に出版された佐谷七段の『現代オセロの最新理論』という書籍です。この書籍はそれまで入門者向けのものがほとんどであったオセロ本の中で、中〜上級者向けの本格的な解説書として画期的でした。これは書籍から盤面をアプリに取り込んで研究するような需要が発生するに違いないと思って、書籍の盤面認識に挑戦することにしました。
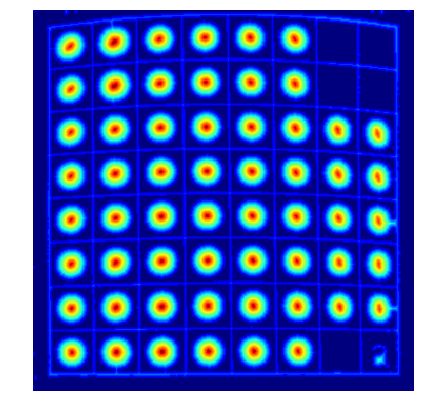
今回は以下のように書籍に印刷された白黒の盤面の石と空きマスを正しく認識することが目標です。

一年前の記事「OpenCVでオセロ盤の盤面を認識する」と同じような処理が必要な部分も多いので、先にそちらをお読みいただくことをお勧めします。
前提環境
- Python 3.7.0 (Anaconda3 5.3.0)
- OpenCV 4.4.0
前回の記事同様、Python版での説明となります。ソースコード全体は以下においてありますのでご参照ください。
https://github.com/lavox/reversi_recognition
方針
- 盤の範囲を特定する
- 正方形に変換する
- 各マスの石の有無を判定する
- 石の色を判定する
各ステップについてこの後説明していきますが、その前に本物の盤と書籍の盤の違いについて整理しておきたいと思います。まずは書籍の方が難しそうな点です。
- 盤の色が緑ではなく白なので、盤の周囲の色や白石の色と同じであり、盤面かどうかの判断が難しい
- 書籍を撮影する際に、紙面が平面とは限らない(湾曲している可能性がある)
- 盤上や石上に説明のための数字や文字が書いてある可能性がある
- 石の形が円形とは限らない
3つ目と4つ目について補足しておくと、以下のように石や盤に数字が書いてあったり、石が菱形になっていたりする場合があります。
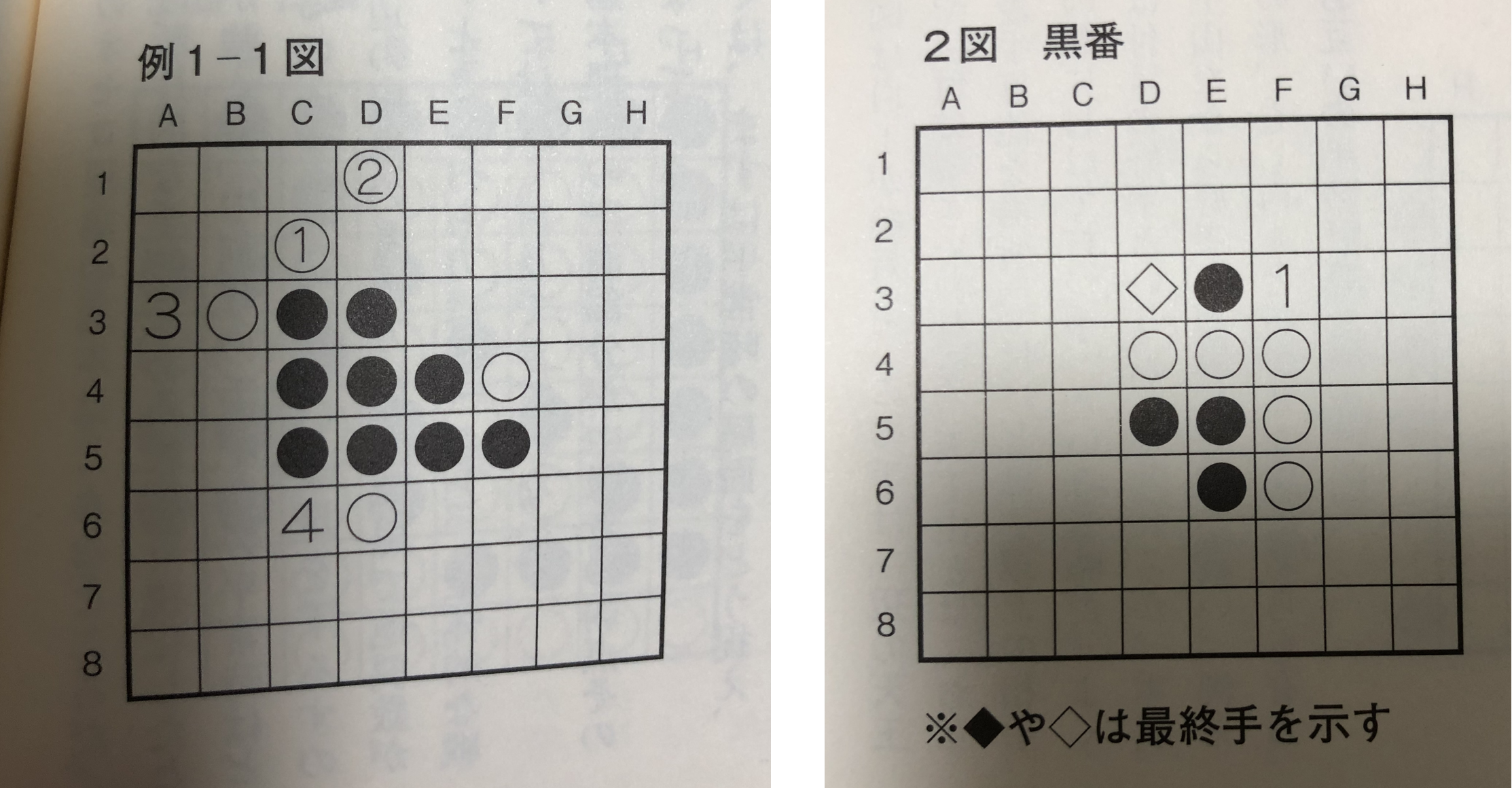
逆に書籍の方が簡単そうな点としては以下が挙げられます。
- 石が反射しない
- 石の厚みがないので斜めから撮っても位置の補正が不要
このような状況を踏まえて、認識に挑戦していきましょう。
準備
まずは画像を読み込みます。今回は白黒の盤で色合いの情報が使えないので、いきなりグレースケール化します。
import cv2
image = cv2.imread("./img/sample2.jpg")
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
Step1.盤面の範囲の特定
まずは画像の中のどこまでが盤面なのかを特定しましょう。前回の本物の盤の時は盤の色が緑だという特徴を使いましたが、今回は盤面は白ですし、ページの盤以外の部分も白なので、その作戦は使えそうもありません。
盤は黒い線でできていて、その周囲は多少なりとも余白があるはずなので、今回は黒い部分のつながりで見る方針にします。
その前に、サンプルで使っている画像でもそうですが、少し影になっているのが邪魔なので、画像の黒い部分と白い部分をはっきりさせるために、前回も石の色の判定で使ったadaptive thresholdを使って画像を二値化します。そして黒い部分だけを取り出します。
import numpy as np
height, width, _ = image.shape
blockSize = int(math.floor((min(width, height) - 1) / 6)) * 2 + 1
blackImage = cv2.adaptiveThreshold(gray, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
cv2.THRESH_BINARY, blockSize, 16)
blackImage = cv2.blur(blackImage, (3,3))
blackImage = cv2.inRange(blackImage, np.array([0]), np.array([216]))
全体としては、adaptiveThresholdで影を取り除いて二値化し、blurで少しぼやかした後、黒い部分をinRangeで少し広めに取っています。
blockSizeが謎の計算をしていますが、おおよそ画像の短辺の1/3にしたい意図です。奇数である必要があるのでちょっと変な式になっています。adaptiveThresholdの最後の値16は微調整により決めた値です。
結果はこんな感じです。黒い部分を取り出したので、結果的に黒かった部分が白に、白かった部分が黒になっています。
この画像について、findContoursで輪郭抽出を行います。
contours, hierarchy = cv2.findContours(blackImage,
cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
抽出された輪郭は複数あるはずですが、あとは本物の盤の時と同じように画像の中央を含む輪郭を取り出し、凸包を取り、approxPolyDPで近似を取るという処理を行うことで盤の範囲を取得することができます。(前回とほぼ同じなので詳細省略)
4頂点がまずまずうまく取り出せました。ただ、紙面が湾曲していたのに4頂点を直線でつないでしまっているため、少しはみ出す状況が生じています。これについては次のステップ以降で考慮して進めます。
Step2.盤面部分を正方形に変換
盤の範囲が特定できたので、前回と同様切り出して正方形にします。前回とちょっと違うのは、マージン部分について塗りつぶさずに画像そのままにしておくというところです。これによって、紙面の湾曲で直線からはみ出してしまった部分も残すことができます。
vertexは前のStepで求めた4頂点、width,heightは同じ値で正方形の盤の一辺の長さ、marginは周囲の余白の長さとしています。
# 変換元の各頂点
src = np.array(vertex, dtype=np.float32)
# 変換後の各頂点
dst = np.array([
[margin, margin],
[width - 1 - margin, margin],
[width - 1 - margin, height - 1 - margin],
[margin, height - 1 - margin]
], dtype=np.float32)
# 変換行列
trans = cv2.getPerspectiveTransform(src, dst)
# 変換
board = cv2.warpPerspective(image, trans, (int(width), int(height)), \
flags=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT, borderValue=(96))
以下は変換結果です。わかりやすくするために、単純に等間隔に8*8の点を赤で印をつけています。湾曲のせいで実際のマスの交点とちょっとずれていることがわかりますが、ひとまず正方形に(近く)できました。

Step3.各マスの石の有無の判定
前回はここで「石の位置の特定」を行いましたが、今回は「各マスの石の有無の判定」としています。この微妙な表現の差は何かと言うと、前回は実際の盤と石だったので、石が必ずしもマスの中心にあるわけではないという想定で進めました。今回は書籍に印刷された盤面なので、さすがに石はマスの中心に印刷されているだろうという仮定をおきました。紙の湾曲のせいでマス自体は単純な格子の位置からはずれていますが、マスの交点の位置さえ正しくわかれば、石の中心はマスの中心(重心)にあるはずだということです。
さて、石の位置を判定するのに、前回は盤の範囲を緑色で抽出して、緑色までの距離で判断を行っていました。今回もそこは同じような判断を行いたいところですが、残念ながら盤面の範囲というのが前回ほど簡単には得られません。盤の色は白ですが、白石の色も白なので、白を抽出するだけでは盤の部分なのか石の部分なのか判断がつかないからです。
そこで今回は以下の作戦で盤の範囲を抽出することにしました。
- Step3-1. マスの交点をなるべく正確に特定する
- Step3-2. マスの交点の周辺の白い部分は盤とみなす
- Step3-3. さらにその連結している範囲も盤とみなす
書籍によっては石が大きめで、マスの辺の部分と石の円周がかなり近づいて接してしまうかもしれないですが、各マスの4隅周辺から連結範囲を抽出すれば、盤面部分が網羅できるはず、という考え方です。
Step3-1. マスの交点をなるべく正確に特定する
先ほど盤の範囲を大体正方形にしたときに単純に等間隔の8*8の点を打ってみましたが、マスの線の交点と比べるとちょっとずれていて、そのままStep3-2,3-3に進むのはちょっと不安があります。
ただ、それほどずれているわけでもないので、この単純格子点の周辺で交点っぽい点を探すというアプローチで精度を上げることにしてみます。
線の交点っぽいところを探すためには、ハフ変換で線を探すという手法もあると思いますが、前回嫌な思い出があるのでそれは避けることにしました。現在の状況として、多少カーブしているとは言え大体縦横に線が走っているので、仮の格子点周辺でx座標、y座標ごとにみたときに黒いピクセルが多い点を取れば交点が得られそうです。ただ黒石に誤爆してしまわないように注意する必要がありそうです。なので、まずは輪郭線的なものを抽出してみることにします。
まずは正方形画像を改めて二値化し、黒部分を少し強調したあと黒い部分を抽出します。目的は黒のベタ塗り部分をなくしつつ線が消えないようにするということなので、黒部分について外側からの距離を取って、その極値的なものを取ればうまくいくのではないかと思い、試行錯誤の結果以下のような処理になりました。
# 二値化
binBoard = cv2.adaptiveThreshold(board, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, 81, 2)
# 黒を強調
binBoard = cv2.erode(binBoard, _KERNEL3)
# 黒領域
black = cv2.bitwise_not(binBoard)
black = cv2.erode(black, _KERNEL3)
# 黒領域の外部からの距離
dist = cv2.distanceTransform(black, cv2.DIST_L2, 5)
# そのラプラシアン
lap = cv2.Laplacian(dist, cv2.CV_32F)
# 負の部分が線っぽい領域
edges = cv2.inRange(lap, np.array([-255.0]), np.array([-1.0]))
もっと良いやり方があるかもしれませんが、ベタ塗り部分を消して線だけ残すことには成功しました。
あとは仮の格子点周辺でx座標、y座標ごとに見てピクセル数の多い座標を抽出します。
GAP = 15 # 想定される交点の位置から許容するずれの範囲
STAT_RANGE = 18 # 交点を求めるために統計を取る範囲の幅
corner = np.array([[[0, 0]] * 9 for i in range(9)])
# まずは内部の交点(外枠以外)について、交点を判定する
for j in range(1, 8):
for i in range(1, 8):
# 交点のX座標調査用の調査範囲
minX = max(BOARD_MARGIN + i * CELL_SIZE - GAP, 0)
maxX = min(BOARD_MARGIN + i * CELL_SIZE + GAP, IMAGE_SIZE)
minY = max(BOARD_MARGIN + j * CELL_SIZE - STAT_RANGE, BOARD_MARGIN)
maxY = min(BOARD_MARGIN + j * CELL_SIZE + STAT_RANGE, IMAGE_SIZE - BOARD_MARGIN)
cornerEdges = edges[minY : maxY, minX : maxX]
# その範囲で、線っぽい領域が最も多いX座標が交点のX座標とする
cornerX = int(np.argmax(np.sum(cornerEdges, axis=0))) + minX
# 同様にY座標についても求める
minX = max(BOARD_MARGIN + i * CELL_SIZE - STAT_RANGE, BOARD_MARGIN)
maxX = min(BOARD_MARGIN + i * CELL_SIZE + STAT_RANGE, IMAGE_SIZE - BOARD_MARGIN)
minY = max(BOARD_MARGIN + j * CELL_SIZE - GAP, 0)
maxY = min(BOARD_MARGIN + j * CELL_SIZE + GAP, IMAGE_SIZE)
cornerEdges = edges[minY : maxY, minX : maxX]
cornerY = int(np.argmax(np.sum(cornerEdges, axis=1))) + minY
corner[i, j] = np.array([cornerY, cornerX])
ちょっとややこしいですが、やっていることは以下のような感じです。
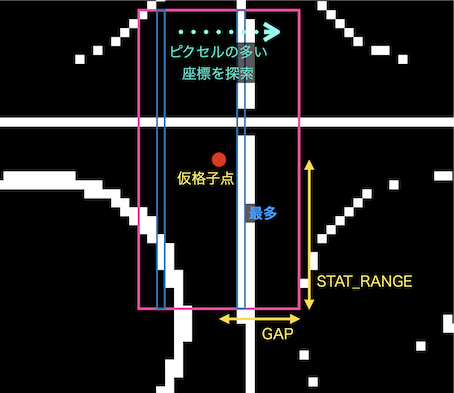
これをX方向、Y方向の両方に対して実行し、交点っぽいところを探しています。またループの範囲が実は1〜7で辺の部分を除いて内側の部分のみ実行しているのですが、辺の付近は線が途切れていることと周囲に座標の文字があったりすることもあって誤検知しやすいからです。
辺周りについては、多少の誤差は許容して内部の点を延長して求めることにしました。
# 隅の四点
corner[0, 0] = corner[1, 1] + (corner[1, 1] - corner[2, 2])
corner[0, 8] = corner[1, 7] + (corner[1, 7] - corner[2, 6])
corner[8, 0] = corner[7, 1] + (corner[7, 1] - corner[6, 2])
corner[8, 8] = corner[7, 7] + (corner[7, 7] - corner[6, 6])
# それ以外の外枠の交点
for i in range(1, 8):
corner[0, i] = corner[1, i] + (corner[1, i] - corner[2, i])
corner[8, i] = corner[7, i] + (corner[7, i] - corner[6, i])
corner[i, 0] = corner[i, 1] + (corner[i, 1] - corner[i, 2])
corner[i, 8] = corner[i, 7] + (corner[i, 7] - corner[i, 6])
結果は以下のようになりました。辺周りがやはり若干誤差が出ていますが、単純な格子点から比べれば大分正確になりました。

Step3-2. マスの交点の周辺の白い部分は盤とみなす
先ほど求めた交点を中心に菱形を描きます。
cornerMask = np.zeros((IMAGE_SIZE, IMAGE_SIZE), dtype=np.uint8)
MASK_SIZE = 11 # マスクの大きさ
for j in range(0, 9):
for i in range(0, 9):
pt = np.array([
[corner[i, j, 1] - MASK_SIZE, corner[i, j, 0]],
[corner[i, j, 1], corner[i, j, 0] - MASK_SIZE],
[corner[i, j, 1] + MASK_SIZE, corner[i, j, 0]],
[corner[i, j, 1], corner[i, j, 0] + MASK_SIZE],
])
cv2.fillConvexPoly(cornerMask, pt, 255)
こんな感じです。この菱形と重なる部分で白いピクセルは白石ということはないはずなので盤とみなして良いでしょう。菱形ではなく円でも良かったのですが、石が基本的には円形なのでなるべくぶつからずに広く取れるようにということで菱形にしてみました。
Step3-3. さらにその連結している範囲も盤とみなす
Step3-2で求めた菱形と重なり合う白色部分と連結した白色部分を盤とみなせば良いはずなので、まずは白色部分を連結成分に分けて、菱形で作ったマスク画像内に含まれる連結成分を抽出します。
# 白色の部分を連結成分に分ける
labelnum, labelimg, data, center = cv2.connectedComponentsWithStats(binBoard, connectivity=8, ltype=cv2.CV_16U)
# 外部とみなすのは、cornerMaskの領域なので、そのindexの集合を取得する
outIdx = np.unique(labelimg[cornerMask != 0])
outIdxが盤とみなすべき白色連結成分のインデックスです。あとはoutIdxの画像を集めていけば良いです。本当はfor文はoutIdxだけ回せば良いですが、それ以外の白色成分についても後で使うので全部のインデックスについて回しています。「★」のコメントをつけた部分は後で使うための処理で、Step3-3のためには必要ありません。
# 外部領域用
outer = np.zeros((IMAGE_SIZE, IMAGE_SIZE), dtype=np.uint8)
# 各マスの内部の白色領域の面積取得用
areaIn = np.zeros((8, 8), dtype=np.uint32) #★
for i in range(1, labelnum):
x, y, w, h, s = data[i]
if np.in1d( i, outIdx ):
# 外部領域のindexリストにあれば、外部領域にマージ
outer = cv2.bitwise_or(outer, cv2.inRange(labelimg, i, i))
elif ( x >= BOARD_MARGIN and x < IMAGE_SIZE - BOARD_MARGIN and y >= BOARD_MARGIN and y < IMAGE_SIZE - BOARD_MARGIN ):
# それ以外は内部の石の領域と思われるため、面積をマス毎に加算する
cell_i = int((x - BOARD_MARGIN) / CELL_SIZE)
cell_j = int((y - BOARD_MARGIN) / CELL_SIZE)
if ( cell_i >= 0 and cell_i < 8 and cell_j >= 0 and cell_j < 8 ): #★
areaIn[cell_j, cell_i] += s #★
結果は以下の通りです。
白石の白部分を排除して、盤の白部分だけを抽出するのに成功しました。
あとはこれの補集合が石(線とか文字とかも一部含まれてしまいますが)なので、本物の盤の時と同じように外側からの距離を求めれば各マスの石の有無が特定できます。
# 内部領域(外部以外の領域)。これで黒石も白石も塗りつぶされる
inner = cv2.bitwise_not(outer)
# その外からの距離を取得
dist = cv2.distanceTransform(inner, cv2.DIST_L2, 5)
各マスの中心(補正した交点の重心)の値が一定値以上かどうかで石の有無が判断できそうです。
Step4.石の色の判定
残るは石の色の判定です。本物の盤のときは光の反射問題に悩まされましたが、今回は紙面に印刷された盤なので反射しません(光沢紙に印刷されたものとかでなければ)。なので、比較的簡単に判定できそうです。
先ほど白色の連結成分について盤とそれ以外(基本的には白石のはず)を分類しましたが、その白色部分の面積がある程度あれば白石という判定をします。そのために先ほどのロジック内でareaInという変数を用意して、マス毎の盤以外の白色の面積を求めていました。ただ、白が少しでもあれば白石かというとそうではなくて、黒石に説明のための数字が白抜きで書かれていたりするので、ある一定値以上ある場合に白石とみなすことにします。
for j in range(0, 8):
for i in range(0, 8):
# マスの中心の座標は、周囲の4交点の重心とする
center = ((corner[i, j] + corner[i + 1, j + 1] + corner[i + 1, j] + corner[i, j + 1]) / 4).astype(np.int32)
# 中心の距離の値が11.5未満の場合は石ではないとみなす(説明のための数字が書いてある等)
if dist[center[0], center[1]] < 11.5:
continue
centerPos = (center - np.array([BOARD_MARGIN, BOARD_MARGIN])) / (CELL_SIZE * 8)
index = np.array([j, i])
if areaIn[j, i] > 100:
# 内部領域が多い場合は白石
self._setDisc(result, DiscColor.WHITE, centerPos, index)
else:
# 少ない場合は黒石
self._setDisc(result, DiscColor.BLACK, centerPos, index)
このロジック内で実はStep3で説明した石の有無も判定しています(中心の距離の値の判定し、一定値未満だったらcontinueして石の色の判定はしていません。つまり空きマスと扱っています)。
おわりに
今回は精度の評価はきちんと行ってはいませんが、その後出版された書籍についても概ね認識できているので体感的な精度はまずまずと思っています。ただカラー印刷の書籍についてはうまく対応できていません(これは本物の盤のアルゴリズムを使ってもうまくいきません)。このあたりが残っている課題です。
これまでの説明で感じていただけたのではないかと思いますが、本物の盤の認識と、書籍の盤の認識では似ている部分もありますが、結構違うアプローチをしないとうまくいきません。そういうこともあって、書籍の盤の認識に対応できているアプリはあまりないのが現状ですが、本記事が多少なりとも役に立つと幸いです。
例によって細かい説明がしきれていない部分もありまので、興味のある方はソースコードをご覧ください。今回の白黒盤面だけでなく、前回の本物の盤の認識も含んだソースコードになっています。