AHC056参加記・13位解法

先日行われたAtCoderのヒューリスティックコンテストHACK TO THE FUTURE 2026(AHC056)にて、13位に入ることができました。本記事では、その解法の紹介と参加記をまとめます。

前半に解法を、後半では参加記を紹介します。

問題概要

今回の問題は、$N\times N$の二次元平面上に設定された$K$個の目的地にロボットを順次到達させるために、ロボットの遷移規則(状態遷移、色の塗り替え、移動)を設計するという問題です。

• ロボットは整数値の内部状態を持つ
• 平面上の各マスは整数値の色がある
• ロボットはマスの色を塗り替えつつ移動する
• 遷移規則は、現在の状態とマスの色に対して、次状態・そのマスの塗り替え色、移動方向を設定する
• 遷移規則をうまく設定して、$K$個の目的地に順番に到達するようにする
• 「内部状態の種類数＋マスの色の種類数」を最小化する

詳細は以下をご参照ください。

冒頭でも触れましたが、筆者は13位でした。以下のグラフは横軸が$K/N^2$(目的地の密度)、縦軸が相対スコアで、筆者を含む11〜15位の参加者をプロットしたものです。筆者はオレンジの線です。

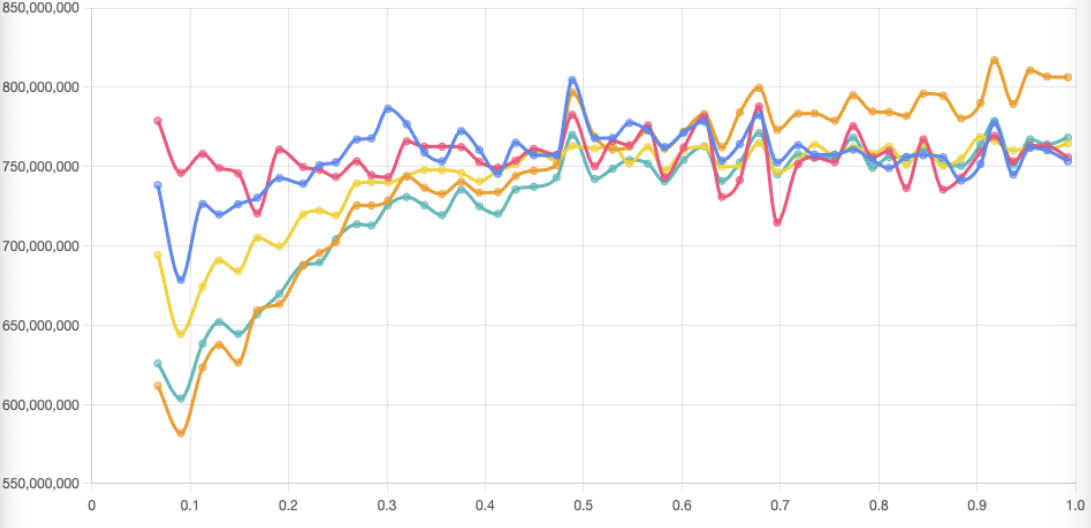
同一順位帯の方と比較して、目的地密度が高い場合が強く、低い場合の弱いという特徴が見て取れます。その点を踏まえて読んでいただけると幸いです。

解法

全体像

使用する規則の種類数を削減するため、内部状態$q$によって移動方向が決定され、内部状態や色は変更しない
$$
(c,q) \rightarrow (c,q,D_q)
$$
のような規則を2色$(c=0,1)$に対して割り当て、これを多くのマスで共通利用する方針にしました。（公式解説動画では「氷の床解法」と呼ばれていました）

ロボットの全体の経路は、この固定色以外の可変マスで制御します。その詳細は次項で説明します。

解法全体は以下の3つのパートからなります。

1. 盤面の固定パターンを構築する
2. ロボットの移動経路を決定する
3. 遷移規則を再利用しながら詰め込む

以降、各パートについて説明します。

盤面の固定パターン構築パート

基本的な盤面パターン

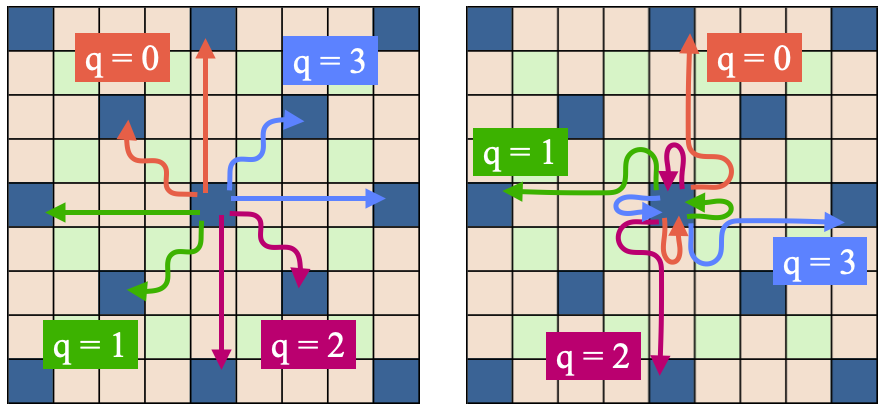
基本方針として、色0には「$q$に応じて直進する」固定遷移を割り当て、色1にはそれを90度回転した方向を割り当てることにしました。
配置パターンは下図のようにしました。オレンジが色0、緑が色1で、青マスは制御用に別の色を割り当てる可変マスです。図の矢印は$q=0$に対応する方向を示しています。

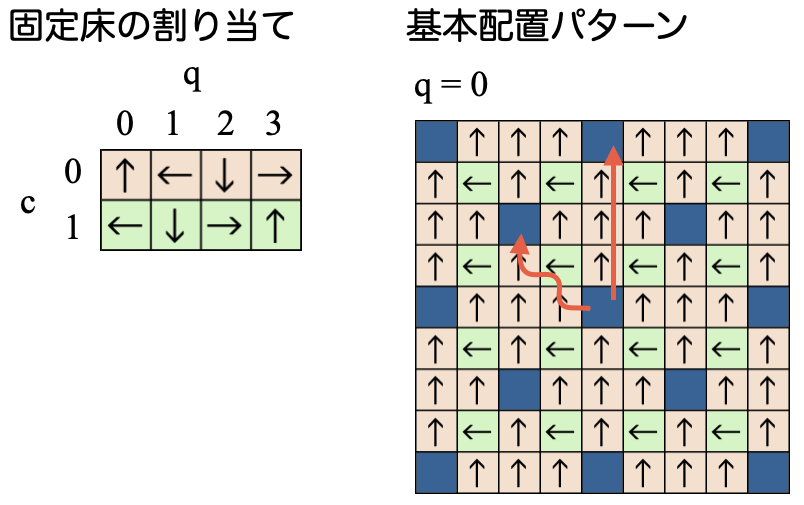
中央の青マスから上方向に$q=0$で進むと、固定色のパターンに従って進み、3マス上の青マスに内部状態$q=0$のまま到達します。
同様に、左方向に$q=0$で進むと左上の青マスに$q=0$のまま到達します。
この構造により、

• 青マスから出る方向(4通り)
• 内部状態$q$の値(4通り)
  の計16通りに対して、周囲8方向(上下左右斜め)と、元のマスの青マスに移動するパスを実現できます。
  

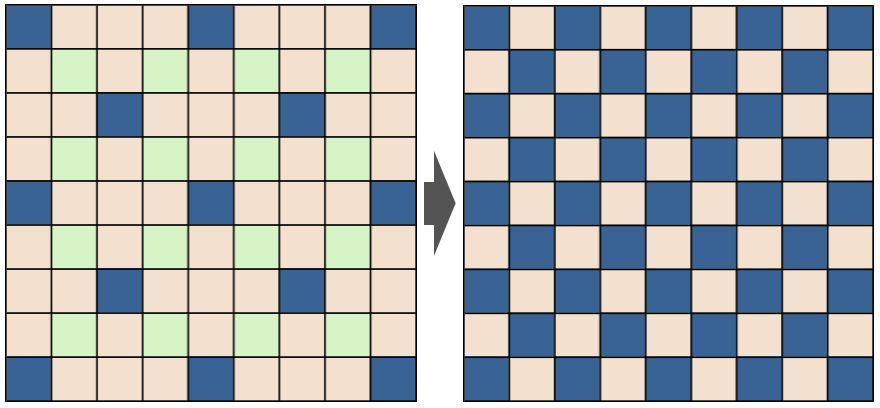
このパターンには以下の特徴があります。

• 固定マス含めて全マスに到達・通過が可能
• 左側の4x2=8パターンは青マス間を最短距離で結んでいる
  • この移動4マス中、可変マスは1マスしか通らないため、遷移規則を約1/4程度に削減できることが期待される
• 目的地が固定マスでも歩数ロスが少ない
  • 右側のパターンがうまく使えればロスを0に押さえられる場合がある
  • そうでなくてもロスは高々4歩程度で済む
• 市松模様へのフォールバックが容易
  • 色0のマスを市松模様と一致させられるので、最大歩数制約$T$に抵触しそうな場合でも、市松模様に切り替えれば探索を継続できる(市松模様は歩数ロスなく経路構築が可能)
    

このパターンは

• 平行移動 8パターン
• 色1の回転方向(左回転/右回転) 2パターン
  の合計16パターンあるため、全通りを時間いっぱい回して改善を行いました。（ランダム要素を経路探索パートや遷移規則詰め込みパートにも入れてバリエーションを作りました）

境界・壁付近の処理

基本パターンは「可変マスを含む行・列」と、「固定マスのみの行・列」が交互に並ぶため、盤面の外周が「固定マスのみ」になってしまうと青マスに戻れず詰むケースが生じます。
また、盤内に壁がある場合も基本パターンだけで埋めると壁にぶつかって動けなくなってしまうケースがあります。

そこで、破綻しないようにするために、以下の処置を行うことにしました。
以下では市松模様の「縦座標＋横座標」が偶数のマスを「偶数マス」、奇数のマスを「奇数マス」と呼び、「奇数マス」＝色0(固定マス)、「偶数マス」＝可変マス(青マス)を含む側とします。

• 壁際は色1→色0に変更
• 角近辺は、曲がれなくなることを回避するために以下の変更を行う
  • 角が偶数マス：角を可変マス(青マス)とする
  • 角が奇数マス：隣接する偶数マスを可変マス(青マス)とする
• 上記の結果色0となるマスは、「上下の2マス先の両方」、「左右の2マス先の両方」のいずれかが可変マスが必要(壁際に限らずこのルールを満たすようにする)
  • 満たさない場合は可変マスを追加する
  • イメージとしては、壁際でも4マスおきに可変マスになるようにする
• 盤面内に配置された壁の先端部の周囲4マスのうち、偶数マスを可変マスとする

これらにより、壁と固定マスの関係で詰むケースを防止しています。
もう少し可変マスの数は節約できるのかもしれませんが、このルールまでで断念しました。

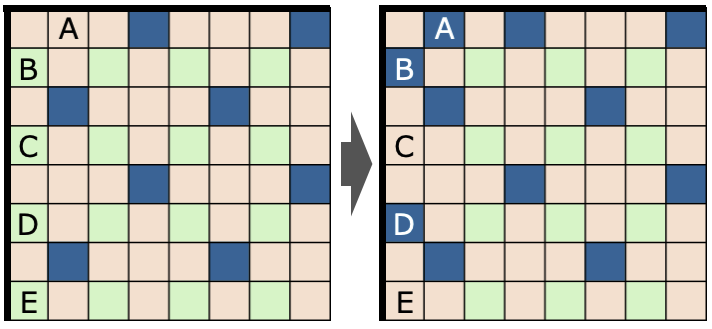
壁際の処理イメージ

• A,B: 角隣接の偶数マス → 可変マス
• D: 4マスに1マス可変マスが必要 → 可変マス
• C,E: 上下2マス先に可変マスがあるため固定マスでOK。色0に変更する。(Eの2マス下は可変マスとする)

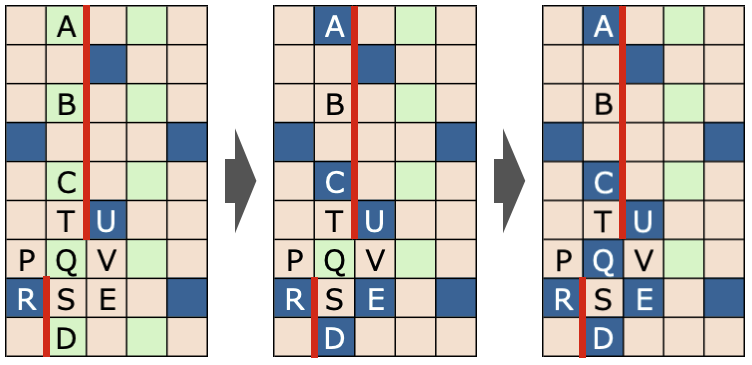
壁の先端の処理イメージ

• まずは前項の壁際ルールを適用
  • D: 角処理 → 可変マス
  • A,B,C: 壁際の4マスに1マスは可変、それ以外は色0
  • E: 「上下2マス先」「左右2マス先」のどちらも可変マスでないマス → 可変マス
• 壁先端部分のルールを適用
  • 壁の先端周囲4マス(PQRS・TUQV)を見て、偶数マスであるQを可変マスとする

壁際処理だけだと(図の2番目の状況)、左上側から右下側に通り抜けることができなくなっています。これを回避するために壁先端付近に可変マスを追加しました。

ロボットの移動経路決定パート

固定マス・可変マスの構造が決まったら、ロボットの移動経路を探索します。
前項の基本パターンにより、可変マスから出る方向×qの値の16パターンで、次の可変マスとそこに至るミニパス(4マス程度)が決まるため、実質的に可変マス間のルートをたどる問題になります。
基本的にはBFSで可能ですが、評価値をつけてダイクストラを使うようにしました。

• 最後の目的地から逆順で経路を決定
• 優先順位は以下の通り
  • 可変マス通過数を最小化
  • 色0/色1と同じ規則が使える可能性のある場合は評価値を上げる
  • その他規則が使い回せる可能性がある場合も評価値を上げる(あまり効果出ず。実装を誤っている可能性あり)
  • 評価値に微小なランダム値を追加し、多様性確保
• 事前に各目的地からの最短距離を求めておき、消費した歩数と残りの最短歩数が制限歩数$T$に近くなったら市松模様にフォールバックして探索を継続
  • 逆順で探索しているため、これが発動した場合、スタート地点からしばらくは市松模様の経路、それ以降は前項で構築したパターンの経路となる
  • マスの視点で見た場合、市松パートで最後に通過する時に基本パターンの固定マスの色に変更するようにすれば、市松パターンから基本パターンに移行できる

これにより、$T$の制約によらず安全に解くことが可能になります。

遷移規則の詰め込みパート

移動経路を決めたあとは、遷移規則をできるだけ再利用しながらCxQのマスに詰め込む処理を行います。
これまで、説明簡略化のためqを4種類としてきましたが、Q=4で固定してしまうとCを非常に大きくする必要があってC+Qを最小化するに当たっては不利になります。
実際には同じ方向に対応するqを複数割り当てて使うことにします。説明の便宜上、固定マスの方向に対応させていたqをvqと読み替えます。
vq=0,1,2,3のそれぞれに対して、複数のqの値を割り当てて使用します。

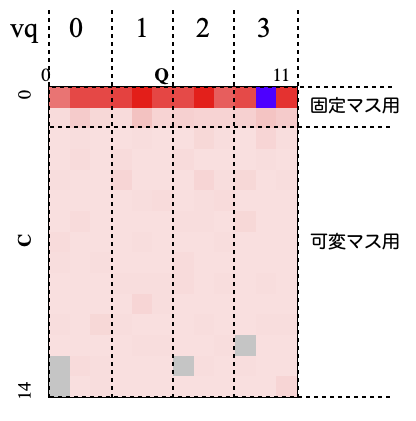
可変要素が多く難しかったので、$C$を仮置きして詰め込みを行いました。$C$はそれまでの最善前後の値(初回は経路に含まれる可変マス長の平方根程度)を使用するようにして何度か試して最善の値を採用するようにしました。

遷移規則と経路の関係は理解が難しいですが、整理すると以下のような対応関係があります。

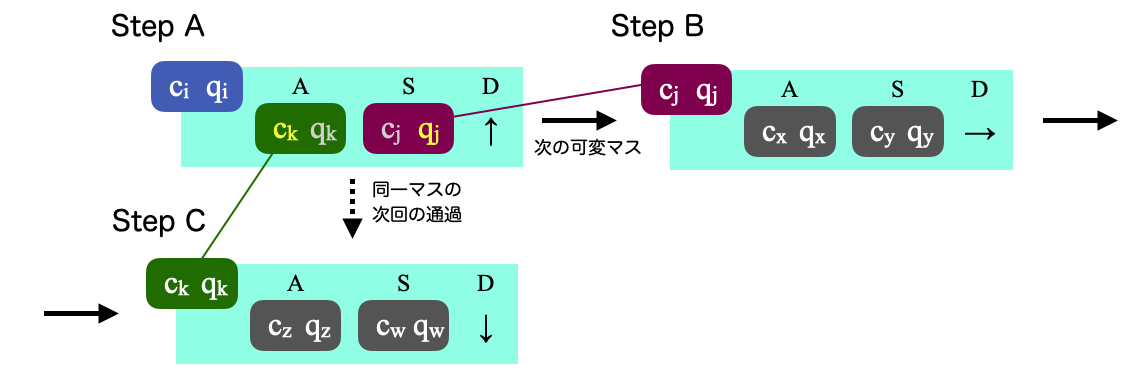
経路が決まると各可変マスに対して次の可変マスに到達するための移動方向Dと状態vqが決まります。Step Aの規則については以下の制約を満たす必要があります。

• 方向D：Step AからStep Bに向かうための方向D
• 次の内部状態S：Step AからStep Bに向かうためのvqに対応する値。この値は次のStep Bのキー(紫)のqと一致する必要がある
• 次の色A：このマスを次に通る際に使用する規則のキー(緑)の色c
• キーの$q_i$の値：このマスに到達するためのvqに対応する値

この観察から、後ろから順に規則を構築していくことができます。規則を決める際にキーcの値は即座に決める必要はなく、遅延して都合の良いように決めることができます。Step Aの規則を決める際には、以下のように行いました。

• 前提として、それまでに割り当てたqの値は具体的に決定済み、cの値は未確定の場合もあるものとする(本当はqも遅延決定させるべきだったと思いますが、複雑すぎて実装を諦めました)
• 固定色c=0,1の規則が利用できる場合は優先的に再利用
• 満たすべき以下の条件と適合可能な規則がすでに存在すれば再利用
  • D=Step Bに向かうための移動方向
  • S=Step Bのキーのqの値
  • A=Step Cのキーのcの値 (少なくとも一方が未確定の場合は一致させることができれば良い)
  • キーのqが前のステップからの遷移のvqに対応する
• 存在しない場合は新たに規則を割り当て
  • D=Step Bに向かうための移動方向
  • S=Step Bのキーのqの値
  • A=Step Cのキーのcの値 (未確定の場合は未確定のまま管理する)
  • キー：qはvqに対応する値を割り当て。cは未確定のまま保留

Cの値を決めた状態で割り当てを行なっているため、割り当て可能なキーの個数は1つのqに対してC-2個までで、それを超える場合は新たにqの値を振り出します。
また規則を再利用する場合、AとStep Cのキーのcが両方未確定の場合、本来は未確定のままにした方が自由度が高いですが、後から具体的な値が割り当てられなくなるケースがあるため、諦めてこの時点で具体的なcを割り当てるようにしました。実装を工夫すればもう少し改善できたかもしれません。

その他の工夫点

これまで説明した内容以外に、以下のような工夫を行いました。

• 基本パターンで、上下左右2マス先の全てに可変マスがあるマスのうち、どこか1マスを色0に固定(一気に8マス動けるルートを作る)
• 幅1の通路の途中の可変マスは色0に固定
• 再利用可能なルールが複数ある場合、その後の再利用性をなるべく低下させないような規則を優先
• $K$が小さい場合は、コンテスト序盤で適当に作った貪欲解の方が強いケースがあったため、両方実行して良い方を採用

参加記

1日目

問題の条件がかなり複雑で、規則の仕組みを理解するのに苦労しました。まずは目的地ごとに異なる内部状態を使用し、マスごとに別の色を割り当てて最短ルートで遷移する解を構築するようにしました。
ちょっとした工夫として、通らなかったマスには色を割り当てないようにして節約しました。
■絶対スコア：18374、40〜50位

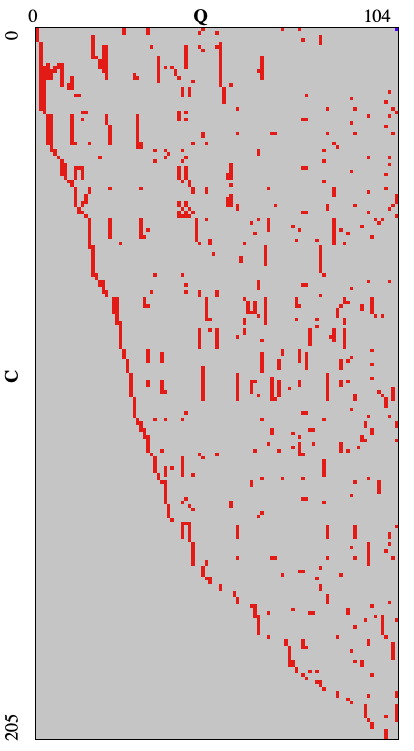
この時点で上位に謎の同点集団ができており、自分のスコアよりも4倍くらい良さそうでした。あまりにも同点で並んでいるので、何か単純なルールベースの良い解があるのだろうと想像しました。
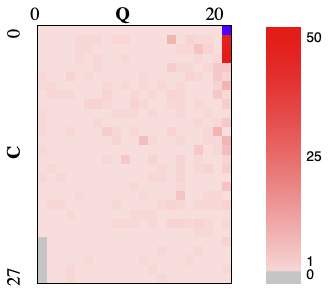
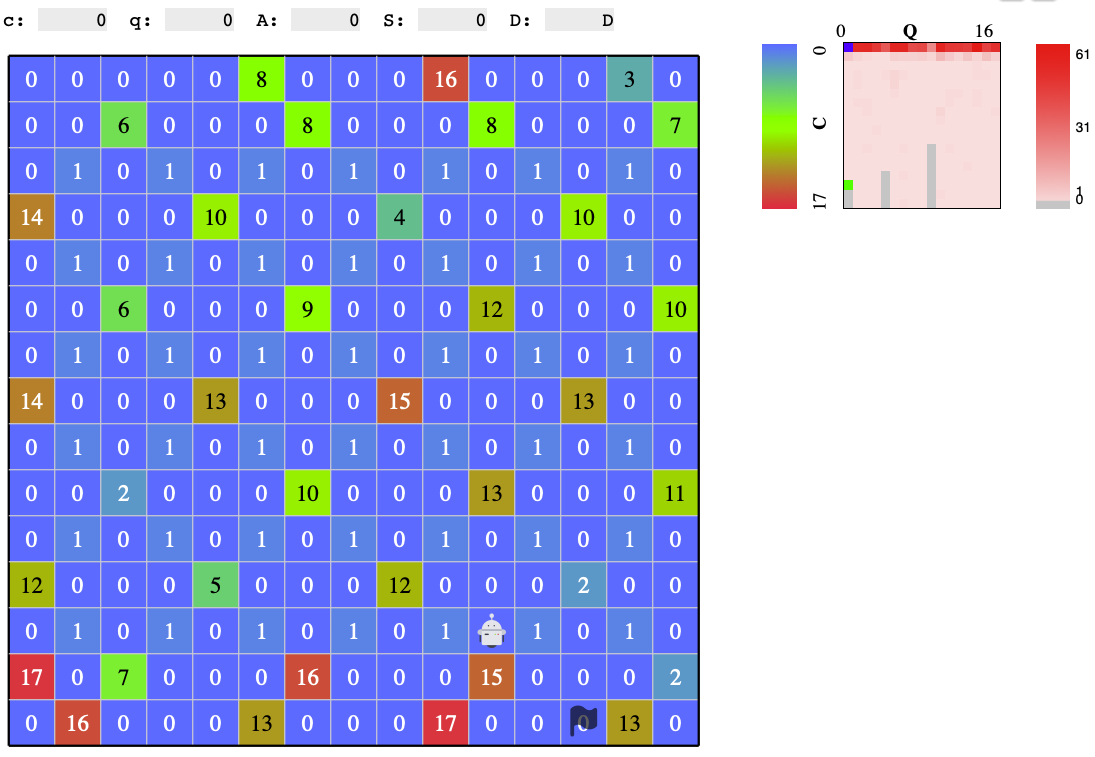
また、ビジュアライザの右側に規則利用状況が表示されていたため、CxQの空白を埋めたいという気持ちになり、単に規則をCxQに順に詰めていけば良いのではないかと思い当たりました。
夜遅かったので、実装は翌日に回しました。

2日目

昨夜思いついた実装を行いました。同一ルールが出現したら再利用したら良いのではというのも寝ながら思いついていたのですが、同点集団が何かを確認しておきたかったので、特に工夫はせずにCxQへの詰め込みを実装しました。結果、予想通り同点集団(いわゆる団子解)に合流することができました。
■絶対スコア：4550、14位

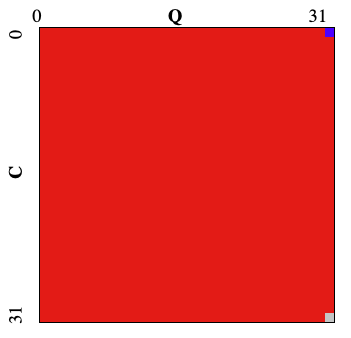
その後、

• 最初は4方向に対して色を割り当てる
• 同一ルールの再利用
• Cの値を色々試して最も良かったものを採用
  の実装を行ったところ、2割くらい改善しました。
  ■絶対スコア：3700、11位
  

方向ごとの4つのルールの再利用率がかなり高いのと、それ以外にもある程度ルールが再利用されていることがわかります。

3日目

この時点で、最上位のスコアは団子解の半分程度でした。規則数に換算すると1歩に1規則を割り当てるのに対して1/4程度にできていることになります。何か劇的に規則数を減らす工夫が必要と考え、4つの色に方向を割り当てて、それを利用して盤面の一部に固定経路を埋め込む方式を考えました(解説放送でベルトコンベア方式と言われていた方法)
特に幅2のエリアを巡回する固定経路を作れば、その部分は常に同じ規則でカバーできるため大幅に節約ができそうです。(以下はseed=10)

しかし、作った固定経路を横断することができないのと、$T$制約に抵触した場合の対応が難しそうなので、この方向性は一旦保留しました。

次に思いついたのが、色0を固定色にしてq毎に方向を割り当て、市松模様に敷き詰める方式です。これなら最短経路で移動することが可能なので、$T$制約に抵触しないというメリットがあります。ただ、これだと規則数は半分程度に節約できますが、スコアに換算すると$1/\sqrt{2}$程度までしか改善できません。

ここで市松模様からさらに可変マスを間引く方向で考察を進めた結果、最終的に採用した「基本パターン」の原型に到達しました。この時点では壁近辺でどのような処理をすれば良いか整理がつかず、一旦壁付近は市松模様として実装しました。
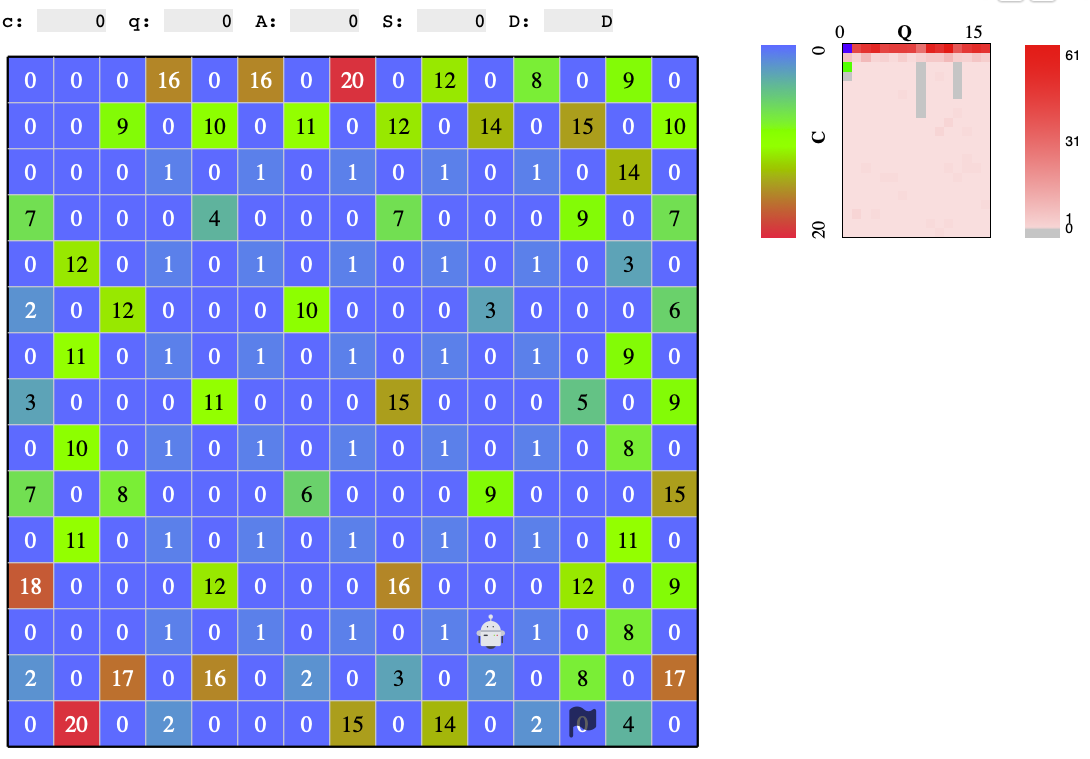
起点位置をずらして良いものを採用するとか、市松模様にフォールバックする実装もここで入れて、大分スコアが改善しました。
■絶対スコア：2893、10位

4〜8日目

平日なのであまり進みませんでしたが、壁近辺が市松模様のままになっているのがあまりにも無駄な感じだったので、到達不可能なマスができないように可変マスの削減を試みました。
この期間で、盤面パターンはほぼ最終形まで改善ができました。

■絶対スコア：2562、29位

スコアは改善しましたが、周りの参加者の改善速度の方が速く、順位は下がってきています。

9日目

盤面パターンによる改善は頭打ちになってきたので、ルールの再利用や詰め込みで改善を図る方向に舵を切りました。
ここまでは、ルールを1つ生成するごとにc,qを順に割り振っていましたが、必要になるまでc,qの決定を遅延させればもっと再利用が図れるのではないかと考えました。キーc,q両方の決定を遅延させたいと考えましたが、実装が難しすぎたので諦めてcだけ遅延させることにしました。それでも実装は大変でしたが何とか完成し、スコアは17%ほど改善し、順位も10位に戻すことができました。
■絶対スコア：2126、10位

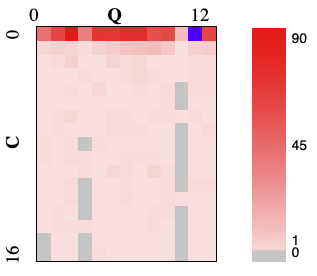
10〜11日目

この後は10%単位の大改善はできなくなり、1%程度の細かい改善を積み重ねました。

• パターン配置の起点ずらしや、色1の回転方向を逆にするのを全部試すようにする
• 幅1の通路の可変マスや、中央付近の可変マス1マスを固定マスに変更する
• 複数のルールが再利用できる場合の優先度付けを実施
• ロジックに乱数要素を取り入れ、時間一杯回すようにする
• 経路探索時に再利用性を多少考慮した評価値を取り入れる
• 可変マスの最後の色は任意なので、それを含めて遅延決定できるようにする
  ■絶対スコア：1940、12位

これが最終提出で暫定12位でしたが、システムテストで1つ順位を下げて最終13位となりました。

おわりに

今回、盤面の見た目が特徴的だったこともあって公式解説動画で紹介いただきました。そんなこともあってモチベーションが上がり、久々に解法記事を作成することにしました。

ご参考になれば幸いです。