この記事は九工大古川研 Advent Calendar 2020 8日目の記事です.
本記事は古川研究室の学生が学習の一環として書いたものです.
内容が曖昧であったり表現が多少異なったりする場合があります.
まえがき
局所線形回帰を完全に理解したい (「い」が大事)というモチベーションで
局所線形回帰について勉強してまとめました.
サークルの後輩も読んでくれるとのことですので
ちょっとクドいくらい丁寧に説明できたらと思っております。
今回は線形回帰の拡張として解説します.
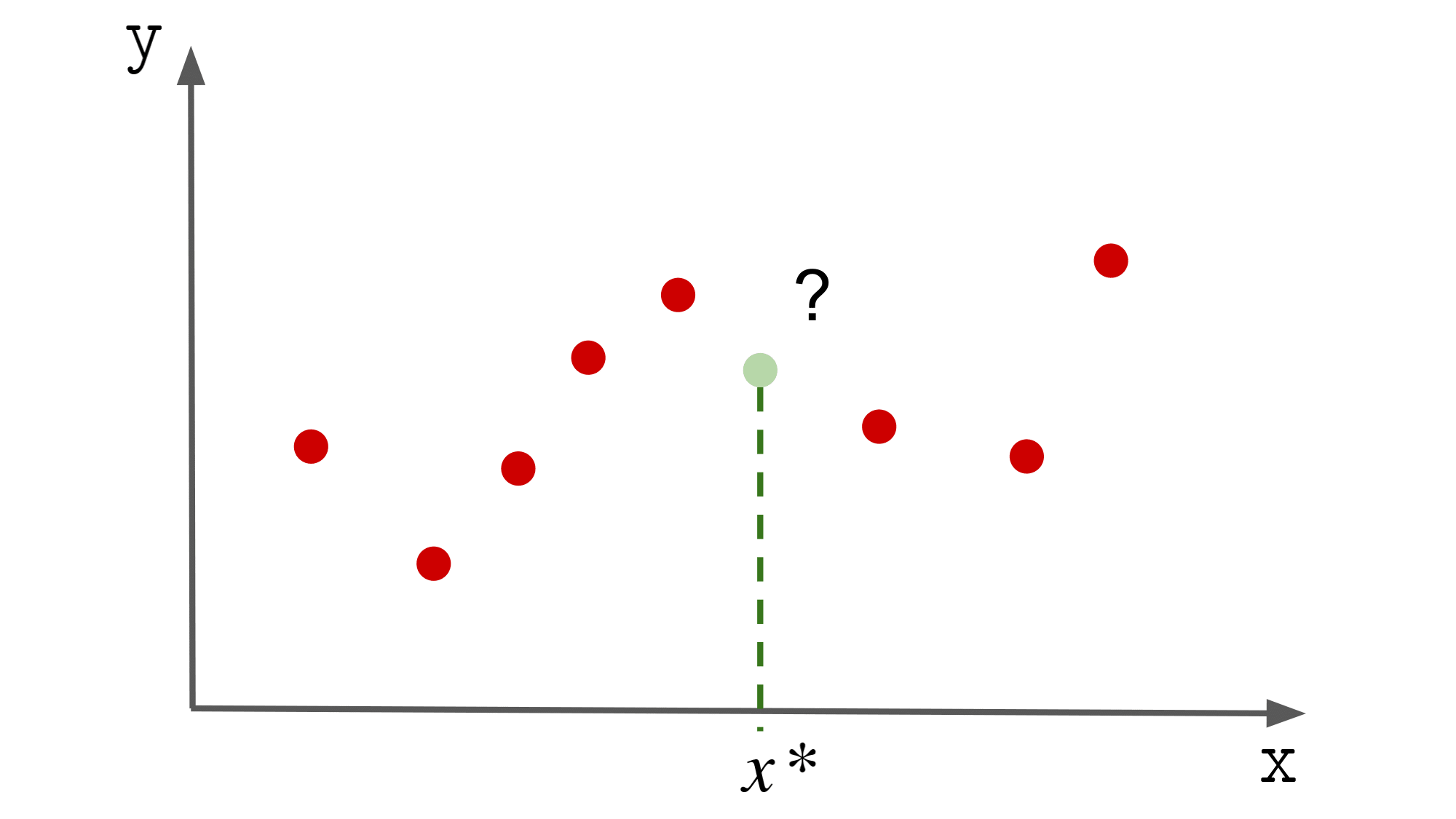
問題設定
${(x_i, y_i)}_{i=1}^{n}$ が与えられているとします.($ x, y$ のペアの集合,$i = 1, \cdots, n$)
ここで,$x$ は入力, $y$ は出力に相当するものです.
与えられた ${(x_i, y_i)}_{i=1}^{n}$ をもとに,
新規の入力 $x^{\ast}$ に対する出力値を予測したいとします.
このときに,$y = f(x)$ となるモデル $f$ をデータから学習しましょうという話です.
線形回帰とは
いわゆる最小二乗法です.
「そんなもんわかっとるわい」という方は
読み飛ばしてもらって大丈夫です.
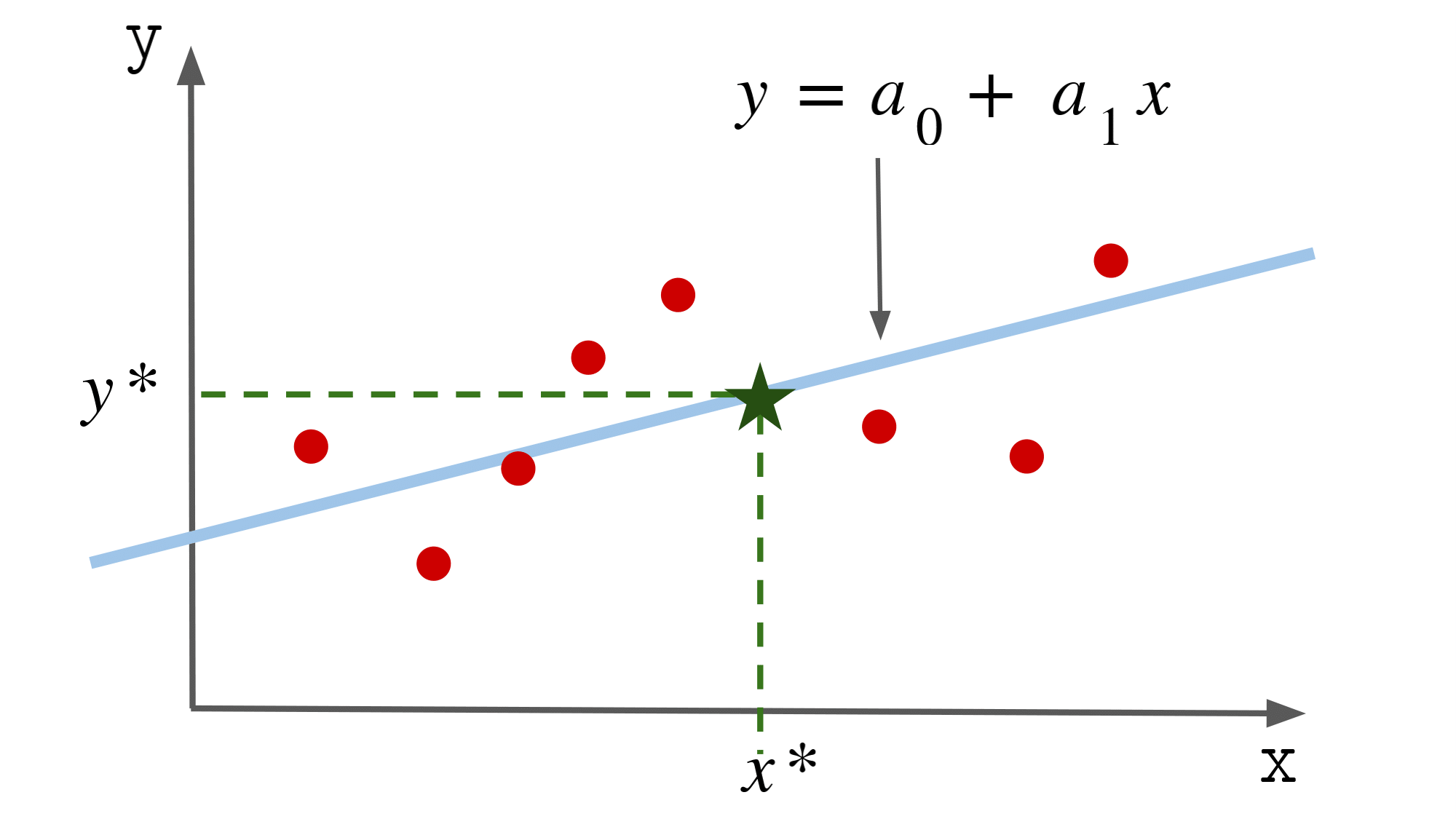
線形回帰では,$ f $ を一次関数として問題を解きます.
具体的には,
$ f(x) = a_0 + a_1 x $ などとおいて,データから $a_0$ と $a_1$ を推定します..
$a_0$ が切片(0次のパラメータ),$a_1$ が傾き(1次のパラメータ)です.
このモデル $f$ を用いて推定した出力を $\hat{y}$ として,
直線の式を以下のように書きます.
\begin{align}
\hat{y} &= a_1 x + a_0 \\
&= \left( \begin{array}{cc} 1 & x \\ \end{array} \right)
\left( \begin{array}{c} a_0 \\ a_1 \end{array} \right) \\
\end{align}
ここで,
\begin{align}
\boldsymbol{x} := \left( \begin{array}{c} 1 \\ x \end{array} \right), \,\,\,
\boldsymbol{a} := \left( \begin{array}{c} a_0 \\ a_1 \end{array} \right)
\end{align}
として,以下のように表します.
y = \boldsymbol{x}^T \boldsymbol{a}
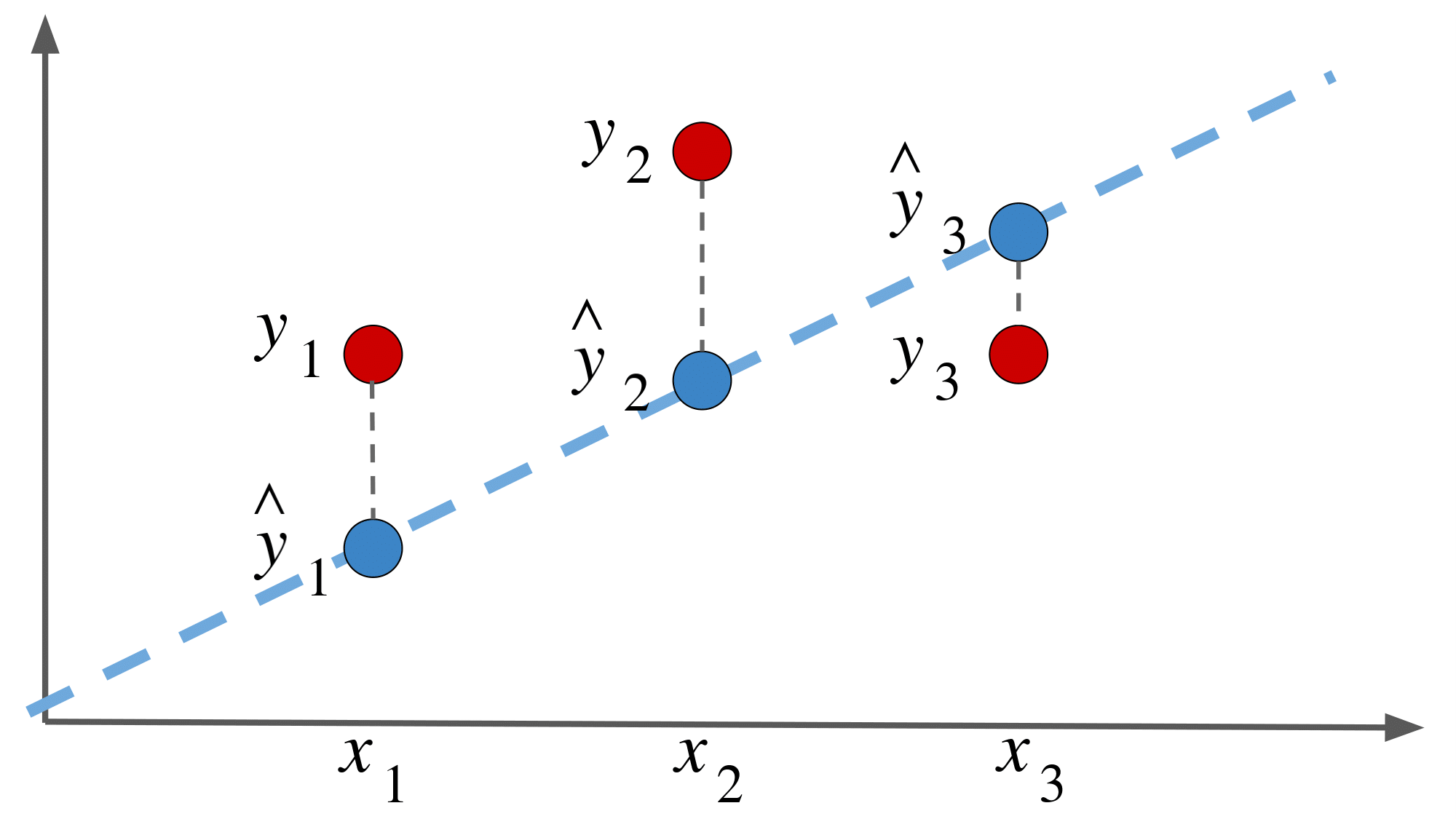
さて,パラメータ $\boldsymbol{a}$ をどうやって決めるのかという話ですが,
ある入力 $x_i$ に対する「出力の推定値 $\hat{y_i}$」 と「実際の出力 $y_i$」 の二乗誤差を
最小にするように $\boldsymbol{a}$ を決めます.
まあこの辺りは調べればいくらでもヒットするような内容ですので多くは語りません.
『ある入力 $x_i$ に対する「出力の推定値 $\hat{y_i}$」 と「実際の出力 $y_i$」 の二乗誤差』の総和を $E$ とします.
いわゆる目的関数です.
\begin{align}
E &= \sum_i^n ( y_i - \hat{y}_i )^2 \\
&= \sum_i^n ( y_i - \boldsymbol{x}_i^T\boldsymbol{a} )^2 \\
\end{align}
$E$ を最小にするようなパラメータ $\boldsymbol{a}$ を求めていきます.
ここで,敢えて $\sum$ を外した形で書いてみます.
E = ( y_1 - \boldsymbol{x}_1^T\boldsymbol{a} )^2 + \cdots + ( y_i - \boldsymbol{x}_i^T\boldsymbol{a} )^2
そしてこれを行列積の形で表現してみると以下のようになります.
E = \left( \begin{array}{cccc} y_1 - \boldsymbol{x}_1^T\boldsymbol{a} & \cdots & y_n - \boldsymbol{x}_n^T\boldsymbol{a} \end{array} \right)
\left( \begin{array}{c} y_1 - \boldsymbol{x}_1^T\boldsymbol{a} \\ \vdots \\ y_n - \boldsymbol{x}_n^T\boldsymbol{a} \\ \end{array} \right) \\
ここで,
\boldsymbol{y} := \left( \begin{array}{c} y_1 \\ \vdots \\ y_n \\ \end{array} \right), \,\,\, \boldsymbol{X} := \left( \begin{array}{c} \boldsymbol{x}_1^T \\ \vdots \\ \boldsymbol{x}_n^T \\ \end{array} \right)
とすることで,以下のような変形ができます.
\left( \begin{array}{c} y_1 - \boldsymbol{x}_1^T\boldsymbol{a} \\ \vdots \\ y_n - \boldsymbol{x}_n^T\boldsymbol{a} \\ \end{array} \right) = \left( \begin{array}{c} y_1 \\ \vdots \\ y_n \\ \end{array} \right) - \left( \begin{array}{c} \boldsymbol{x}_1^T \\ \vdots \\ \boldsymbol{x}_n^T \\ \end{array} \right) \boldsymbol{a} = \boldsymbol{y} - \boldsymbol{X} \boldsymbol{a}
すなわち先程の $E$ 式は以下のように書けます.
\begin{align}
E &= \left( \boldsymbol{y} - \boldsymbol{X}\boldsymbol{a} \right)^T
\left(\boldsymbol{y} - \boldsymbol{X}\boldsymbol{a} \right) \\
&= \left\|\boldsymbol{y} - \boldsymbol{X}\boldsymbol{a} \right\|^2
\end{align}
$\boldsymbol{y} - \boldsymbol{X} \boldsymbol{a}$ のユークリッドノルムの二乗の形ですね.
上で変形した $E$ の式について,
右辺を展開してから $\boldsymbol{a}$ で微分します.
\begin{align}
\frac{\partial}{\partial \boldsymbol{a}} E
&= \frac{\partial}{\partial \boldsymbol{a}}\left( \boldsymbol{y} - \boldsymbol{X}\boldsymbol{a} \right)^T
\left( \boldsymbol{y} - \boldsymbol{X}\boldsymbol{a} \right) \\
&= \frac{\partial}{\partial \boldsymbol{a}}
\left( \boldsymbol{y}^T - \boldsymbol{a}^T\boldsymbol{X}^T \right)
\left( \boldsymbol{y} - \boldsymbol{X}\boldsymbol{a} \right) \\
&= \frac{\partial}{\partial \boldsymbol{a}}
\left( \boldsymbol{y}^T\boldsymbol{y}
- \boldsymbol{y}^T\boldsymbol{X}\boldsymbol{a}
- \boldsymbol{a}^T\boldsymbol{X}^T\boldsymbol{y}
+ \left(\boldsymbol{X} \boldsymbol{a} \right)^T \left(\boldsymbol{X} \boldsymbol{a} \right)
\right) \\
&= 0 - \boldsymbol{X}^T \boldsymbol{y} - \boldsymbol{X}^T \boldsymbol{y} + 2 \boldsymbol{X}^T \boldsymbol{X} \boldsymbol{a} \\
&= - 2 \boldsymbol{X}^T \boldsymbol{y} - 2 \boldsymbol{X}^T \boldsymbol{X} \boldsymbol{a}
\end{align}
となります.
そして,これを最小とする $\boldsymbol{a}$ ,すなわち
\frac{\partial}{\partial \boldsymbol{a}} E = 0
となる $\boldsymbol{a}$ を求めますと,
\begin{align}
- 2 \boldsymbol{X}^T \boldsymbol{y} - 2 \boldsymbol{X}^T \boldsymbol{X} \boldsymbol{a} &= 0 \\
2\boldsymbol{X}^T \boldsymbol{X} \boldsymbol{a} &= 2 \boldsymbol{X}^T \boldsymbol{y} \\
\boldsymbol{a} &= \left( \boldsymbol{X}^T \boldsymbol{X} \right)^{-1}\boldsymbol{X}^T \boldsymbol{y}
\end{align}
となります.
めでたしめでたし.
また,ここで求まった $\boldsymbol{a}$ は
ムーア・ペンローズの一般化逆行列を用いて以下のようにも表現できます.
\boldsymbol{a} = \boldsymbol{X}^{\dagger} \boldsymbol{y}
ただし,$\boldsymbol{X}^{\dagger}$ は以下のように定義されます.
\boldsymbol{X}^{\dagger} := \left( \boldsymbol{X}^T \boldsymbol{X} \right)^{-1}\boldsymbol{X}^T
局所線形回帰に拡張
ここからが本題です.
上で説明した線形回帰では
推定した出力 $\hat{\boldsymbol{y}_i}$ と実際の出力 $\boldsymbol{y}_i$ の誤差を
すべてのデータに対して平等に重み付けしてパラメータを計算していました.
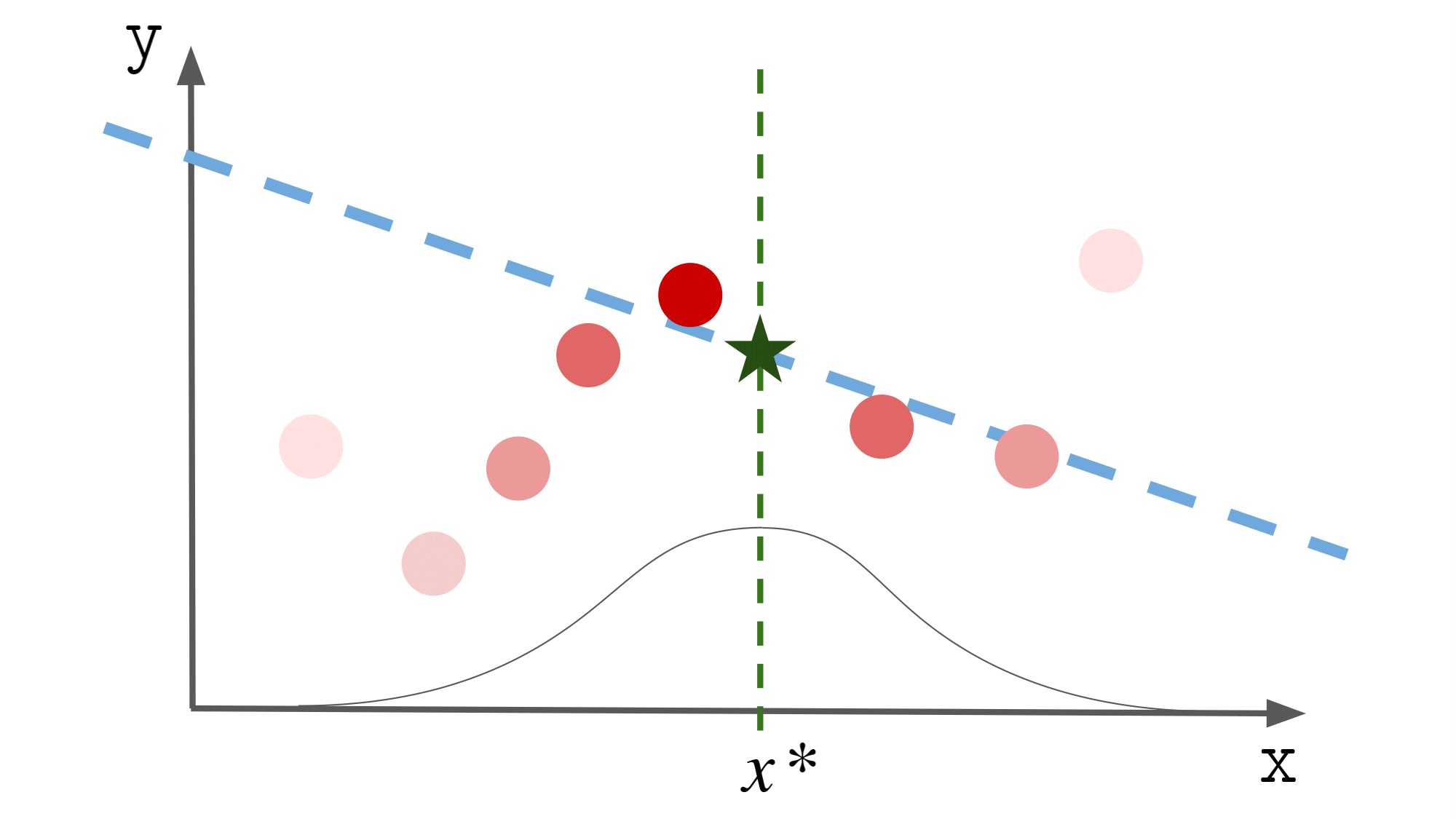
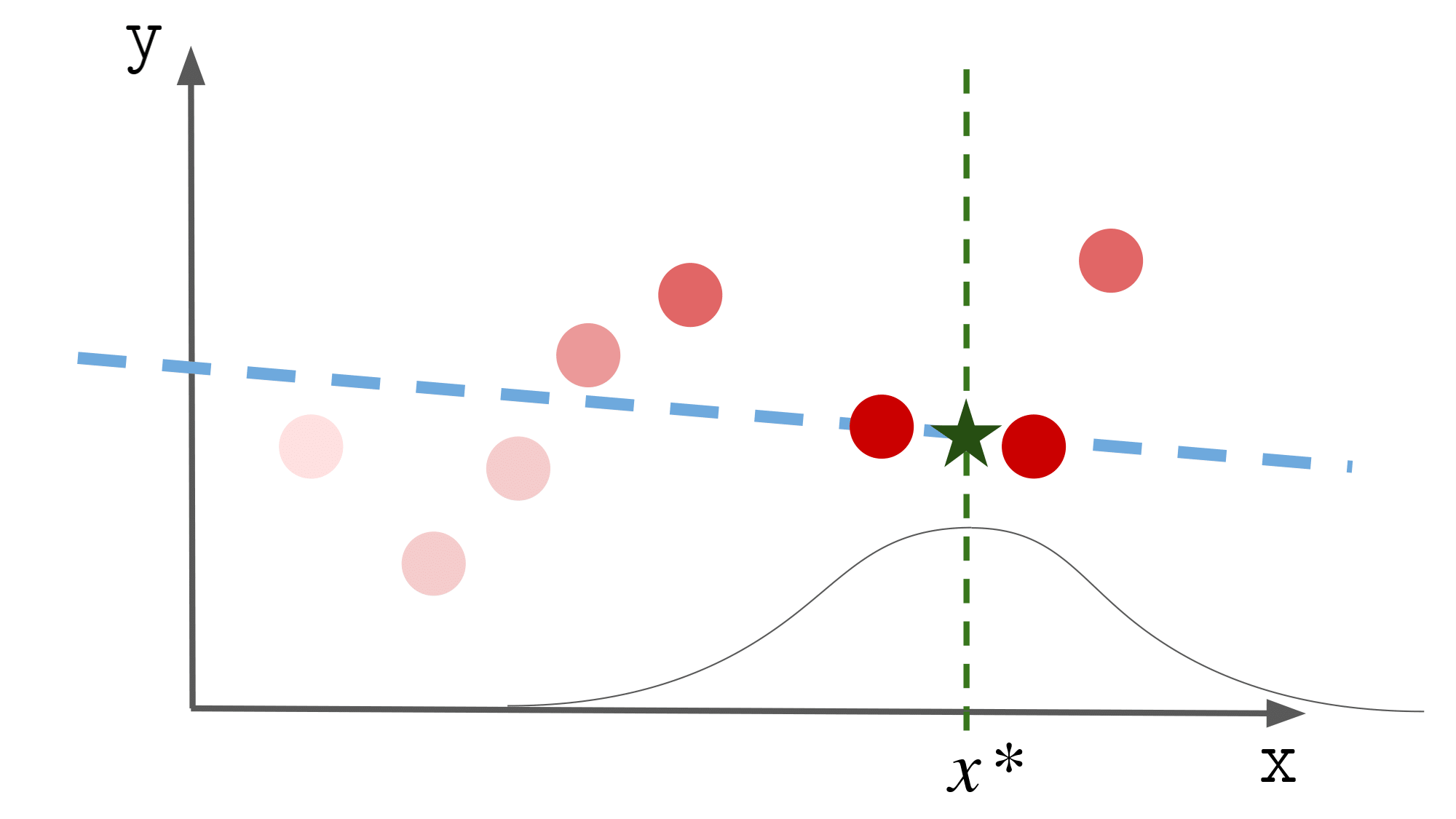
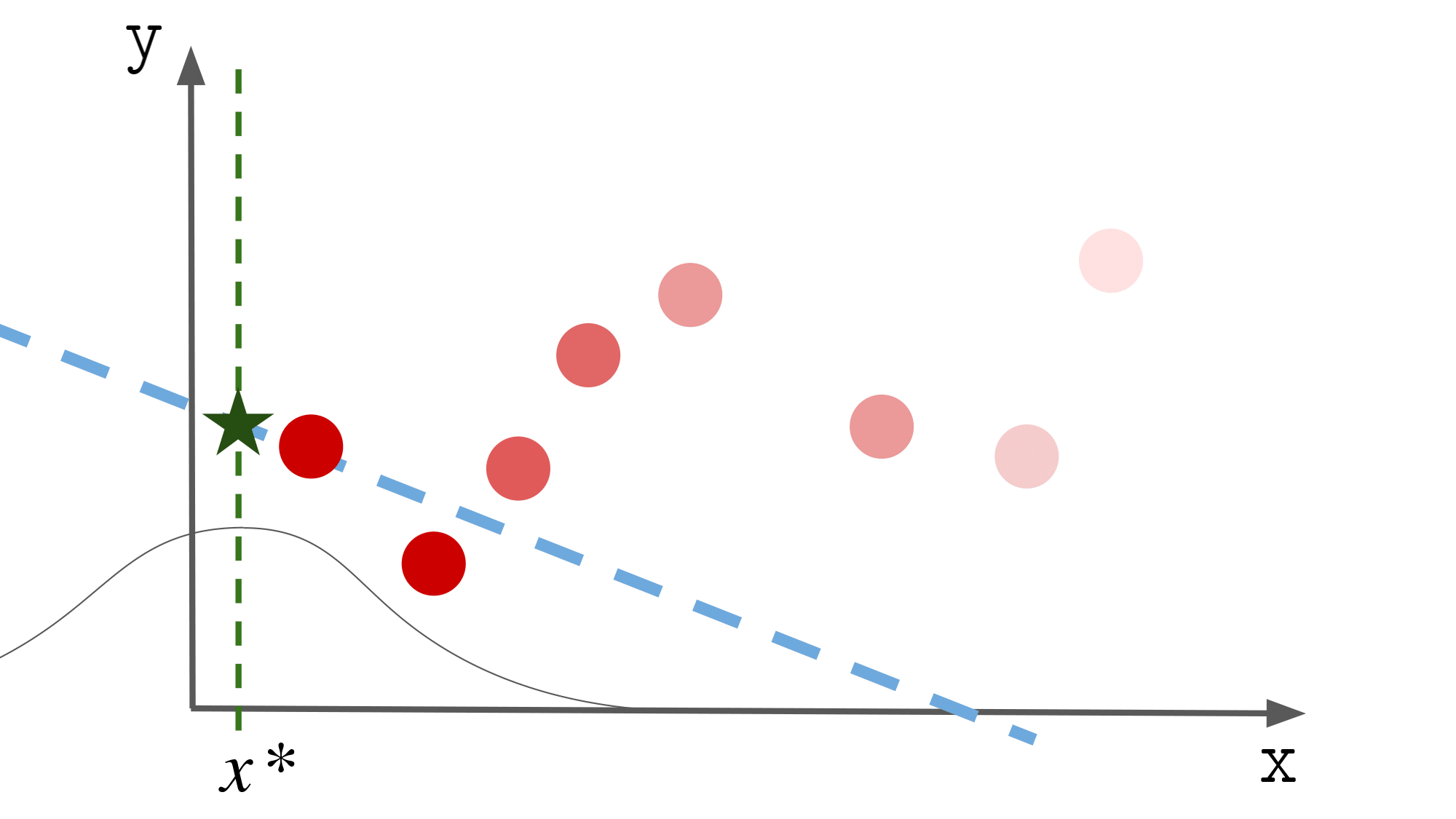
局所線形回帰では,
新規の入力に近いデータに対しては誤差を重く,
逆に遠いデータに対しては誤差を軽く見て
パラメータを計算します.
イメージは以下の図の通りです.
$x^\ast$ の値によってパラメータが異なるのも
なんとなくわかるかと思います.
このときの誤差の重みを決める関数(カーネル関数)$ k(x, x^\prime) $ は
以下の式で表されるとします.
k(x, x^\prime) = \exp \left(- \frac{1}{2 \sigma^2} ( x - x^\prime )^2 \right)
$\sigma$ はカーネル幅と呼ばれる(ハイパー)パラメータで,
ざっくり言いますと
「新規データに対する近い or 遠いを決める境目」を決めるものです.
これを大きくするとより広い範囲のデータを近傍と見なします.
これを究極に大きくすると先程の線形回帰と同じ結果を得られます.
\begin{align}
E &= \sum_i^n k(x^\ast, x_i) ( y_i - \boldsymbol{x}_i^T\boldsymbol{a} )^2 \\
&= \left( \begin{array}{ccc} y_1 - \boldsymbol{x}_1^T\boldsymbol{a} & \cdots & y_n - \boldsymbol{x}_n^T\boldsymbol{a} \end{array} \right)
\left( \begin{array}{ccc}
k(x^\ast, x_1) & & \huge{0} \\
& \ddots & \\
\huge{0} & & k(x^\ast, x_n) \\
\end{array} \right)
\left( \begin{array}{c} y_1 - \boldsymbol{x}_1^T\boldsymbol{a} \\ \vdots \\ y_n - \boldsymbol{x}_n^T\boldsymbol{a} \\ \end{array} \right) \\
\end{align}
ここで
\begin{align}
\boldsymbol{y} &:= \left( \begin{array}{c} y_1 \\ \vdots \\ y_n \\ \end{array} \right)\\[10pt]
\boldsymbol{X} &:= \left( \begin{array}{c} \boldsymbol{x}_1^T \\ \vdots \\ \boldsymbol{x}_n^T \\ \end{array} \right) \\[10pt]
\boldsymbol{W}_{x^\ast} &:= \left( \begin{array}{ccc}
k(x^\ast, x_1) & & \huge{0} \\
& \ddots & \\
\huge{0} & & k(x^\ast, x_n) \\
\end{array} \right)
\end{align}
とおくと以下のように書けます.
E = \left( \boldsymbol{y} - \boldsymbol{X}\boldsymbol{a} \right)^T
\boldsymbol{W}_{x^\ast} \left( \boldsymbol{y} - \boldsymbol{X}\boldsymbol{a} \right)
線形回帰の時と似たような式が出てきましたね.
実際,この式は「$\boldsymbol{W}_{x^\ast}$ をメトリックとするノルム」として
E = \left\| \boldsymbol{y} - \boldsymbol{X}\boldsymbol{a} \right\|_{\boldsymbol{W}_{x^\ast}}^2
とも表現できる(らしい)です.(要出典)
そして,線形回帰の時と同様に
$\boldsymbol{a}$ で偏微分すると以下のようになります.
\begin{align}
\frac{\partial}{\partial \boldsymbol{a}} E &= \frac{\partial}{\partial \boldsymbol{a}} \left( \boldsymbol{y} - \boldsymbol{X}\boldsymbol{a} \right)^T
\boldsymbol{W}_{x^\ast} \left( \boldsymbol{y} - \boldsymbol{X}\boldsymbol{a} \right)\\
&= \frac{\partial}{\partial \boldsymbol{a}} \left( \boldsymbol{y}^T - \boldsymbol{a}^T\boldsymbol{X}^T \right)
\boldsymbol{W}_{x^\ast} \left( \boldsymbol{y} - \boldsymbol{X}\boldsymbol{a} \right)\\
&= \frac{\partial}{\partial \boldsymbol{a}}\left(
\boldsymbol{y}^T \boldsymbol{W}_{x^\ast} \boldsymbol{y}
- \boldsymbol{y}^T \boldsymbol{W}_{x^\ast} \boldsymbol{X}\boldsymbol{a}
- \boldsymbol{a}^T\boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{y}
+ (\boldsymbol{X}\boldsymbol{a})^T \boldsymbol{W}_{x^\ast} \boldsymbol{X}\boldsymbol{a} \right)\\
&= 0 - \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{y} - \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{y} + 2 \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{X} \boldsymbol{a} \\
&= - 2 \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{y} + 2 \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{X} \boldsymbol{a} \\
2 \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{X} \boldsymbol{a} &= 2 \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{y} \\
\boldsymbol{a} &= \left( \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{X} \right)^{-1} \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{y}
\end{align}
結構大変ですね.
目的関数 $E$ をパラメータ $\boldsymbol{a}$ で微分した式が求まりましたので,
\frac{\partial}{\partial \boldsymbol{a}} E = 0
となるような $\boldsymbol{a}$ を求めていきます.
\begin{align}
2 \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{X} \boldsymbol{a} &= 2 \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{y} \\
\boldsymbol{a} &= \left( \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{X} \right)^{-1} \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{y}
\end{align}
ということで,目的関数 $E$ を最小とする
パラメータ $\boldsymbol{a}$ が求められました.
この式も線形回帰の時に求めたものと似ていますね.
「$\boldsymbol{W}_{x^\ast}$ をメトリックとする $\boldsymbol{X}$ の一般化逆行列 」を
\boldsymbol{X}_{\boldsymbol{W}_{x^\ast}}^{\dagger} := \left( \boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{X} \right)^{-1} \boldsymbol{X}^T \boldsymbol{W}_{x^\ast}
のように定義することで
\boldsymbol{a} =\boldsymbol{X}_{\boldsymbol{W}_{x^\ast}}^{\dagger} \boldsymbol{y}
とも書けます.
実際に回帰してみる
Python で実際に回帰させてみます.
コードは最後に載せます.
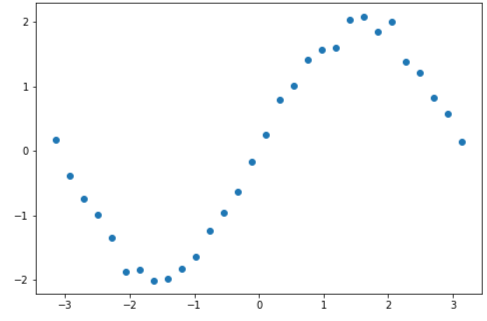
学習データは $y = sin(x) + \epsilon$ ($\epsilon$ はガウシアンノイズ)としました.
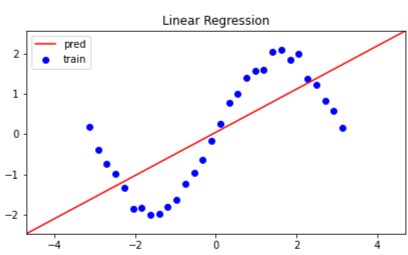
線形回帰
まず線形回帰で推定した場合です.
局所線形回帰
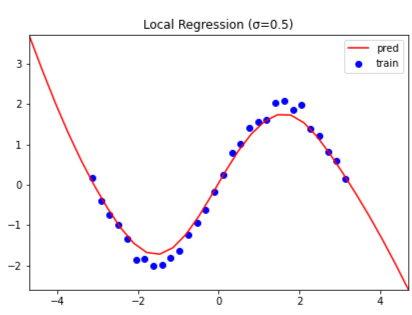
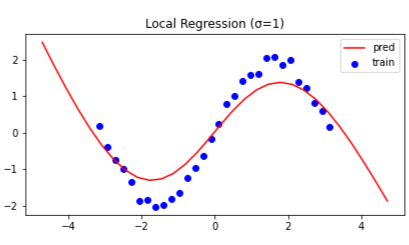
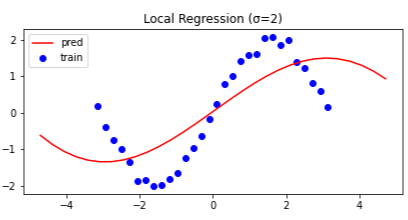
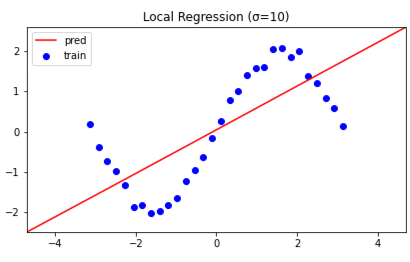
局所線形回帰で推定した場合です.
カーネル幅 $\sigma$ を $\sigma = 0.5, 1.0, 2.0, 10.0$ と変えて比較もしてみました.
($\sigma$ の値は図中に記しております.)
カーネル幅 $\sigma$ が小さいほど,より狭い領域で直線を推定します.
一方で,カーネル幅 $\sigma$ を極端に大きくすると
線形回帰と(ほぼ)同じ推定結果を得られます.
おまけ
局所線形回帰では,ある $\boldsymbol{x}$ に対する出力 $\boldsymbol{\hat{y}}$について,
局所的に一次関数で近似します.
ただ,一次関数にこだわる必要はなくて,
二次関数でも三次関数でもゼロ次(定数)関数でも良いわけです.
このように,局所線形回帰に対し
「局所的に n 次多項式で回帰する」というように
一般化した回帰モデルを「局所多項式回帰」と呼びます.
ちなみに,Nadaraya-Watson カーネル回帰は
局所多項式回帰のゼロ次関数版です.
Nadaraya-Watson is 何?という話は
イモムシ氏が解説してくれていますので
ぜひ読んでみてください.
Nadaraya-Watosonを理解したい
付録:実装まとめ
Jupyter Notebook のままの方が見やすいかなと思いましたので
Gist のリンクを貼ることにしました.
良かったら Google Colab で開いて動かしてみてください.
カーネル幅(最後のセルの sigma)を色々いじって遊んでみると楽しいかも知れません.
カーネル幅を小さくしすぎると
$\boldsymbol{X}^T \boldsymbol{W}_{x^\ast} \boldsymbol{X}$ の逆行列が計算できなくなってコケるので注意です.
ここまで読んでくださってありがとうございました.
コメントなどお待ちしてます.
参考文献
- The Matrix Cookbook
- Trevor Hastie et al.(2014)「統計的学習の基礎 ―データマイニング・推論・予測―」共立出版