【コンピューターサイエンス入門第1回:機械学習やってみる】 k平均法をJavaで実装してみよう～座標の概念について～

はじめに

こんにちは、炭山水です。

前回 【コンピューターサイエンス入門第0回:機械学習やってみる】 k平均法をJavaで実装してみよう の続きを書いていきます。

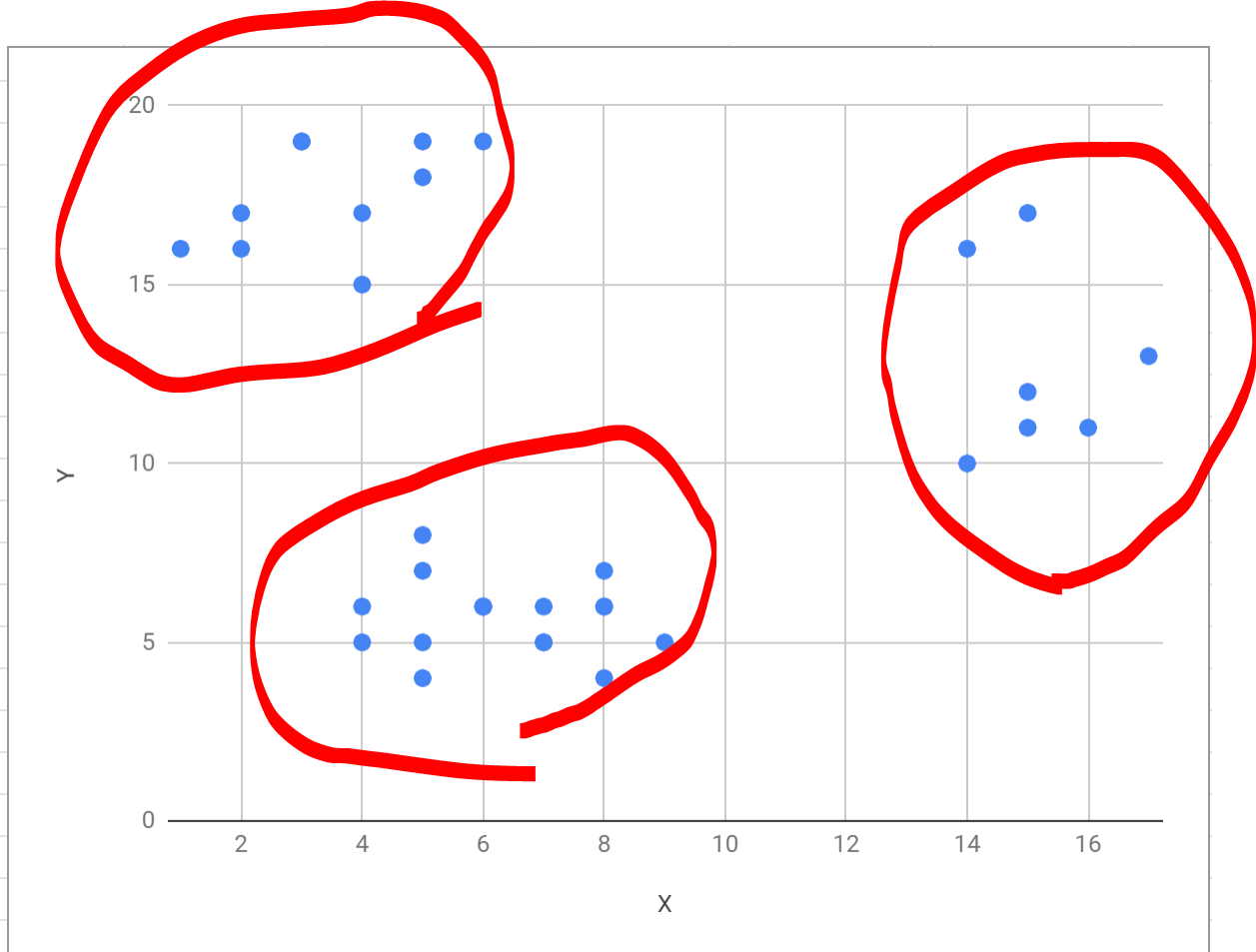
前回の記事で、最終的にクラスタリングでどんなことができるか紹介しました。

第1回の今日は、この点の位置を数値データとして表現するための「座標」という概念を解説＆実装していきます¹

環境

• IntelliJ IDEA
• Java12 + SpringBoot 2.1.6
• JUnit5

この環境の準備についてはこちらの記事で書きました。
IntelliJ+Gradle+SpringBoot+JUnit5(jupiter)で新規開発を始めるときの備忘録

分析対象を数値で表現するということ

第0回 でもお伝えした通り、クラスタリングを行う対象は「ウェブサイトのアクセス時刻と滞在時間」とか「クレジットカードの利用日と利用額」などの実生活に存在する数値データです。

が、クラスタリングという手法を覚えるにあたってはいったん抽象化して平面や立体上の位置だってことにしてしまった方が概念の理解がしやすいので、「そういうこと」にして話を進めてしまいます。

平面上(2次元)の点の位置

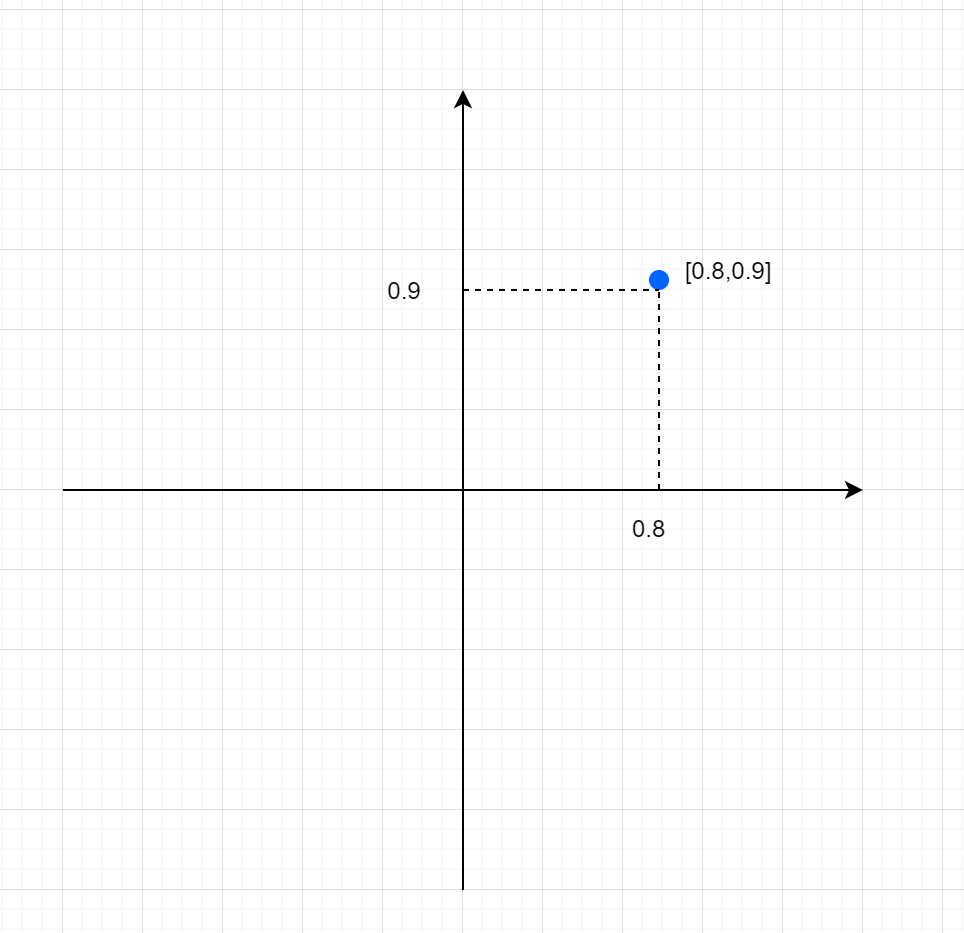
小難しい話はさておいて、図をご覧ください。図の通り、横方向に0.8,縦方向に0.9進んだ場所に置かれた点を[0.8,0.9]と表現します。これを位置ということにしてしまいます。

これで、この適当に配置された点は[0.8,0.9]という数値を持つデータとして扱うことができるようになりました。

立体上(3次元)の位置も一応考慮しておく

もうちょっと拡張しましょうか。

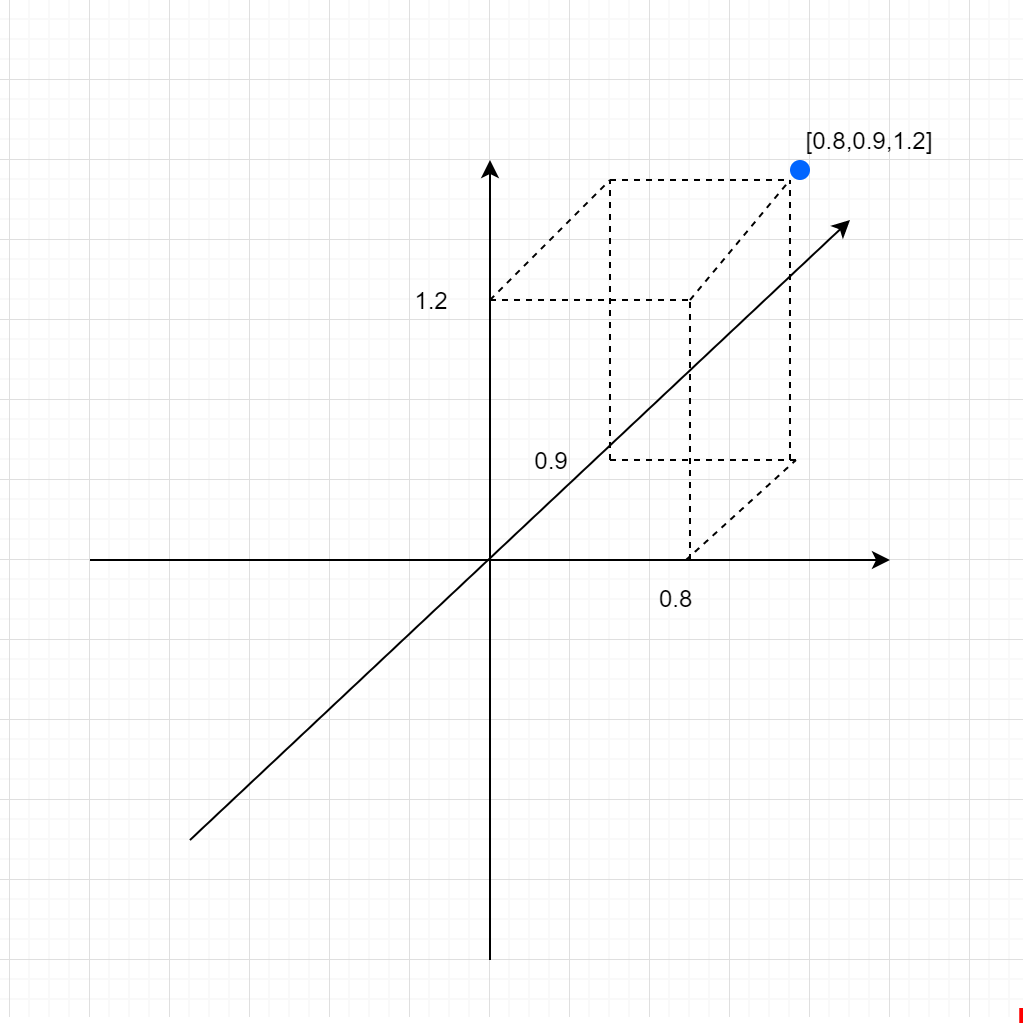
図のように3次元の立体の中で適当に点を置いたら、横0.8,縦0.9,高さ1.2進んだ位置だったとします。そうするとこの点は[0.8,0.9,1.2]という表現ができますね。

その気になれば、4次元だろうが10次元だろうが数字で[0.8,0.9,1.2,1.7,0.1]みたいに表現できるのですが、人間の目にわかる図で描けるのは今のところ3次元がせいぜいなので、図にするのはご勘弁を…。

実装してみよう

僕は最近Javaばっかり触ってるのでJavaで実装しますね。

とりあえず、2次元,3次元,4次元と軸が増えるたびに

• [0.8,0.9]
• [0.8,0.9,1.2]
• [0.8,0.9,1.2,1.7]

と「数値が」「複数保持される」というデータ型になるので、点1つの位置はDouble型のListがいいかと思います。

で、第0回でも書いた通り、複数の点に対して最終的には処理をかけるので、DoubleのListが複数あるということで、

    private final List<List<Double>> points;

こんなフィールドを持つクラスを作ると「分析対象のデータ」をクラスで表現できますね。

あとは、コンストラクタでデータを格納できるようにしていきましょう。

データを格納するときの要件としては、こんな感じになるかなと

• null進むということはあり得ないので、Double型にnullが入っていたらException
• 位置がnullということはあり得ないので、Listにnullが入っていたらException
• コンストラクタ時点でぬるぽが発生したら呼び出し元でハンドリングしてください
• 平面と立体、など次元が異なる点が同居することはあってはいけないので、2次元データと3次元データが混じっていたら、すなわちListのsizeが違うデータが混在していたらException

で、これを実装すると

package net.tan3sugarless.clusteringsample.lib.data;

import lombok.EqualsAndHashCode;
import lombok.Getter;
import lombok.ToString;
import lombok.Value;
import net.tan3sugarless.clusteringsample.exception.DimensionNotUnifiedException;
import net.tan3sugarless.clusteringsample.exception.NullCoordinateException;

import java.util.List;

/**
 * ユークリッド距離空間上の座標集合
 */
@Getter
@ToString
@EqualsAndHashCode
@Value
public class EuclideanSpace {

    private final List<List<Double>> points;

    /**
     * n次元座標のリストをセットする
     *
     * DimensionNotUnifiedException
     * 座標の次元が統一されていないリストをセットした
     *
     * NullCoordinateException
     * 座標の数値にnullが含まれていた
     *
     * NullPointerException
     * nullデータ、もしくはnull要素を含むデータを渡した
     *
     * @param points : n次元座標のリスト
     */
    public EuclideanSpace(List<List<Double>> points){
        if(points.stream().mapToInt(List::size).distinct().count()>1){
            throw new DimensionNotUnifiedException();
        }
        if(points.stream().anyMatch(point -> point.stream().anyMatch(x -> x == null))){
            throw new NullCoordinateException();
        }

        this.points = points;
    }
}

Exceptionは独自に定義しちゃいました。

いきなり「ユークリッド」とか用語が出てきますが、空間とかなんとか言い始めると話が脱線するのでスルーしてください。

んで、コンストラクタのテストも書いておきます。

package net.tan3sugarless.clusteringsample.lib.data;

import net.tan3sugarless.clusteringsample.exception.DimensionNotUnifiedException;
import net.tan3sugarless.clusteringsample.exception.NullCoordinateException;
import org.junit.jupiter.api.Assertions;
import org.junit.jupiter.api.DisplayName;
import org.junit.jupiter.params.ParameterizedTest;
import org.junit.jupiter.params.provider.Arguments;
import org.junit.jupiter.params.provider.MethodSource;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;
import java.util.stream.Stream;

public class EuclideanSpaceTest {

    //全体 null,空,要素1つ,要素複数
    //各要素 null含む,空含む,すべて空(0次元),1次元,n次元
    //各要素内の座標 null含む,0含む,null含まない
    //次元チェック すべて同じ次元,異なる次元
    static Stream<Arguments> testConstructorProvider(){
        return Stream.of(
            Arguments.of(null,new NullPointerException()),
            Arguments.of(Collections.emptyList(),null),
            Arguments.of(Arrays.asList(Arrays.asList(1.5,-2.1)),null),
            Arguments.of(Arrays.asList(Arrays.asList(1.2,0.1),Arrays.asList(0.0,1.5)),null),
            Arguments.of(Arrays.asList(null,Arrays.asList(0,1.5),Arrays.asList(-0.9,0.1)),new NullPointerException()),
            Arguments.of(Arrays.asList(Arrays.asList(-0.9,0.1),Arrays.asList(0.0,1.5),Collections.emptyList()),new DimensionNotUnifiedException()),
            Arguments.of(Arrays.asList(Collections.emptyList(),Collections.emptyList(),Collections.emptyList()),null),
            Arguments.of(Arrays.asList(Arrays.asList(1.5),Arrays.asList(0.0),Arrays.asList(-2.2)),null),
            Arguments.of(Arrays.asList(Arrays.asList(1.5,2.2,-1.9),Arrays.asList(0.0,0.0,0.0),Arrays.asList(0.9,5.0,2.2)),null),
            Arguments.of(Arrays.asList(Arrays.asList(1.5,null,-1.9),Arrays.asList(0.0,0.0,0.0),Arrays.asList(0.9,5.0,2.2)),new NullCoordinateException()),
            Arguments.of(Arrays.asList(Arrays.asList(1.5,2.1,-1.9),Arrays.asList(0.0,0.0),Arrays.asList(0.9,5.0,2.2)),new DimensionNotUnifiedException()),
            Arguments.of(Arrays.asList(Arrays.asList(2.1,-1.9),Arrays.asList(0,0,0),Arrays.asList(0.9,5.0,2.2)),new DimensionNotUnifiedException())

        );
    }

    @ParameterizedTest
    @MethodSource("testConstructorProvider")
    @DisplayName("コンストラクタのテスト")
    void testConstructor(List<List<Double>> points, RuntimeException e){
        if(e==null){
            Assertions.assertDoesNotThrow(()->new EuclideanSpace(points));
        }else{
            Assertions.assertThrows(e.getClass(),()->new EuclideanSpace(points));
        }
    }
}

これでJavaのクラスで「任意の次元に置かれた点の集合」を表現することができるようになりました。

ここで書いたコードはGitHubに置いてあります。

※たぶんこの後クラスいじりまくるので、Tagで残しておきました

次回は「点と点がどれだけ離れているか」をJavaで表現する方法について解説します。

では次回！ここまで読んでいただいてありがとうございました。

次回
【コンピューターサイエンス入門第2回:機械学習やってみる】 k平均法をJavaで実装してみよう～データ同士の距離～

1. 本当は順序が逆なんですが(数値データを見た目わかりやすく2次元空間に表現してるだけ)、わかりやすさ重視のため多少厳密性に欠けるのはご容赦ください。 ↩