LoginSignup
2
1

More than 3 years have passed since last update.

@tan3_sugarless(炭 山水)inTECH::Survivor

【コンピューターサイエンス入門第2回:機械学習やってみる】 k平均法をJavaで実装してみよう～データ同士の距離～

Last updated at Posted at 2019-07-27

はじめに

こんにちは、炭山水です。

前回の続きです。
【コンピューターサイエンス入門第1回:機械学習やってみる】 k平均法をJavaで実装してみよう～座標の概念について～

前回は平面や空間上にデータを配置する座標の概念と、それをJavaで表現するところまでやってみました。

今回はデータ同士の距離の概念についてお話しします。

環境

  • IntelliJ IDEA
  • Java12 + SpringBoot 2.1.6
  • JUnit5

この環境の準備についてはこちらの記事で書きました。
IntelliJ+Gradle+SpringBoot+JUnit5(jupiter)で新規開発を始めるときの備忘録

改めて考えると距離ってなんだ

第0回でもお伝えした通り、要するにクラスタリングでやりたいことって近いデータをまとめるということなわけですが、じゃあデータ同士が近いってなんだということを定義してあげる必要があります。

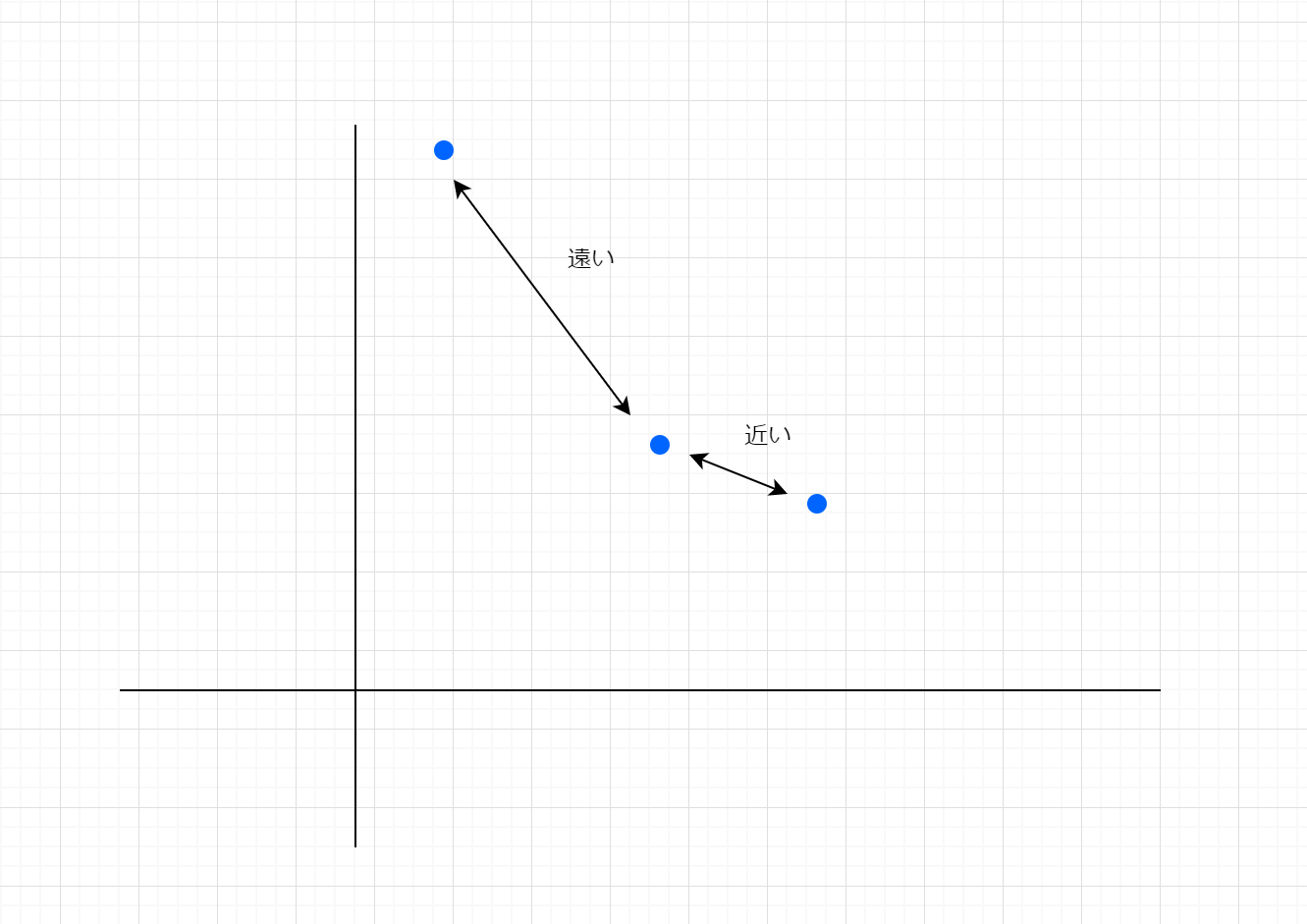
例えば図のような場合

image.png

人間の目で見るとまあ、一目瞭然なわけですが、計算するのはコンピュータですので、近い/遠いを数値で表現してあげるわけですね。

そこでコンピュータでは、距離(distance)という値を用いることで、

  • 距離の値が大きければ遠い
  • 距離の値が小さければ近い

という風に数値で比較することができるようになります1。

ユークリッド距離を使おう

実は距離の計算方法はそれだけで研究が成り立つほどたくさんあるのですが、今回は計算しやすく仕組みが視覚的にわかりやすいユークリッド距離というものを使います。

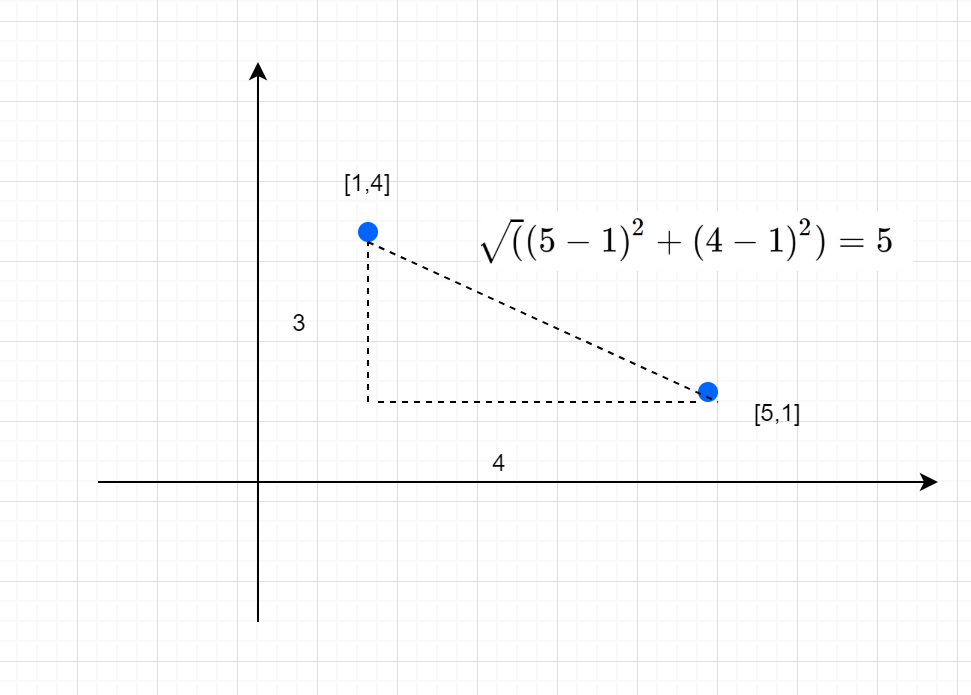
御大層な名前をしていますが、要するに2点間を定規で測ったときにわかる普通の距離です。が、コンピュータにデータごとに定規を使わせるわけにもいかないので、計算で算出します。

image.png

図をご覧ください。三平方の定理を覚えていますでしょうか。要はアレです。
[1,4]という座標に配置された点と[5,1]という座標に配置された点は、横方向(各座標一つ目の要素)と、縦方向(各座標二つ目の要素)の差の2乗の、合計の、平方根をとると5という距離が出ます。

ちなみに3次元でももっと高次元でも同じ方法で計算できるのでいくらでも拡張できます。

[3,1,2]と[1,0,6]という3次元における距離は、
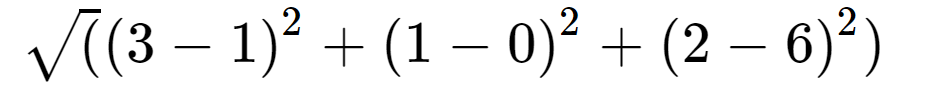
image.png
となります。次元が増えると足す数をその分増やせばOKです。

実装してみよう

package net.tan3sugarless.clusteringsample.lib.data;

import lombok.EqualsAndHashCode;
import lombok.Getter;
import lombok.ToString;
import lombok.Value;
import net.tan3sugarless.clusteringsample.exception.DimensionNotUnifiedException;
import net.tan3sugarless.clusteringsample.exception.NullCoordinateException;

import java.util.List;
import java.util.Objects;
import java.util.stream.Collectors;

/**
 * ユークリッド距離空間上の座標集合
 */
@Getter
@ToString
@EqualsAndHashCode
@Value
public class EuclideanSpace {

    private final List<List<Double>> points;
    private final int dimension;

    /**
     * n次元座標のリストと次元をセットする
     *
     * @param points : n次元座標のリスト
     * @throws DimensionNotUnifiedException : 座標の次元が統一されていないリストをセットした
     * @throws NullCoordinateException      : 座標の数値にnullが含まれていた
     * @throws NullPointerException         : nullデータ、もしくはnull要素を含むデータを渡した
     */
    public EuclideanSpace(List<List<Double>> points) {
        if (points.stream().mapToInt(List::size).distinct().count() > 1) {
            throw new DimensionNotUnifiedException();
        }
        if (points.stream().anyMatch(point -> point.stream().anyMatch(Objects::isNull))) {
            throw new NullCoordinateException();
        }

        this.points = points;
        this.dimension = points.stream().findFirst().map(List::size).orElse(0);
    }

    /**
     * 任意の座標からの、このインスタンスに格納された各座標の距離を算出する
     *
     * @param target 各座標からの距離を出したい基準点の座標
     * @return targetからのユークリッド距離を表すリスト
     * @throws DimensionNotUnifiedException : targetとインスタンスの次元が異なる
     * @throws NullCoordinateException      : targetにnullを含む
     */
    public List<Double> distanceFromTarget(List<Double> target) {
        if (target.size() != dimension) {
            throw new DimensionNotUnifiedException();
        }

        if (target.stream().anyMatch(Objects::isNull)) {
            throw new NullCoordinateException();
        }

        return points.stream().map(point -> {
            double squareOfDistance = 0.0;
            for (int i = 0; i < target.size(); i++) {
                squareOfDistance += Math.pow(point.get(i) - target.get(i), 2);
            }

            return Math.sqrt(squareOfDistance);
        }).collect(Collectors.toList());
    }
}

前回と同じクラスに作っていきます。

まず、次元のチェックをしやすくするためにコンストラクタとフィールドをちょっと改修しました。

    private final int dimension;

intフィールドに次元を格納できるようにしたのと、

        this.dimension = points.stream().findFirst().map(List::size).orElse(0);

取得したデータが何次元が計算するロジックの追加ですね。

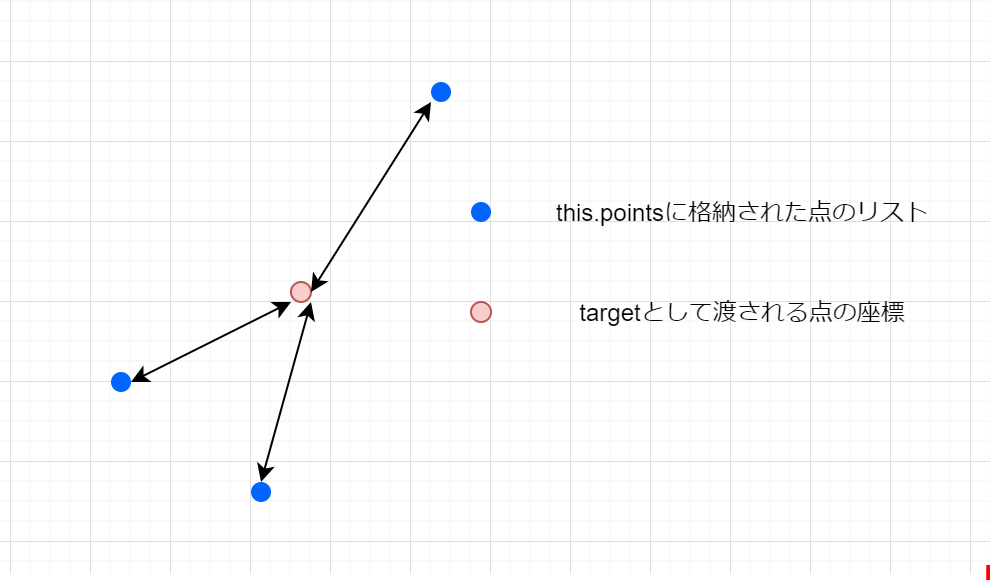
で、実際に距離を算出するメソッドがこちら。今後の実装で「とある点と全部の座標に対する距離」を算出したいのでこのようなかたちになってます。

    /**
     * 任意の座標からの、このインスタンスに格納された各座標の距離を算出する
     *
     * @param target 各座標からの距離を出したい基準点の座標
     * @return targetからのユークリッド距離を表すリスト
     * @throws DimensionNotUnifiedException : targetとインスタンスの次元が異なる
     * @throws NullCoordinateException      : targetにnullを含む
     */
    public List<Double> distanceFromTarget(List<Double> target) {
        if (target.size() != dimension) {
            throw new DimensionNotUnifiedException();
        }

        if (target.stream().anyMatch(Objects::isNull)) {
            throw new NullCoordinateException();
        }

        return points.stream().map(point -> {
            double squareOfDistance = 0.0;
            for (int i = 0; i < target.size(); i++) {
                squareOfDistance += Math.pow(point.get(i) - target.get(i), 2);
            }

            return Math.sqrt(squareOfDistance);
        }).collect(Collectors.toList());
    }

いきなりMath::powとかMath::sqrt出てきてますが、powは累乗、sqrtは平方根をとるメソッドです。MathはWebサービスとか業務アプリケーションであんまりなじみのないクラスですが算術計算でよく使うので覚えていてくださいね。

図示するとこういうことがしたい感じです。

image.png

そしてテスト

package net.tan3sugarless.clusteringsample.lib.data;

import net.tan3sugarless.clusteringsample.exception.DimensionNotUnifiedException;
import net.tan3sugarless.clusteringsample.exception.NullCoordinateException;
import org.junit.jupiter.api.Assertions;
import org.junit.jupiter.api.DisplayName;
import org.junit.jupiter.params.ParameterizedTest;
import org.junit.jupiter.params.provider.Arguments;
import org.junit.jupiter.params.provider.MethodSource;

import java.util.Arrays;
import java.util.Collections;
import java.util.List;
import java.util.stream.Stream;

class EuclideanSpaceTest {

    //全体 null,空,要素1つ,要素複数
    //各要素 null含む,空含む,すべて空(0次元),1次元,n次元
    //各要素内の座標 null含む,0含む,null含まない
    //次元チェック すべて同じ次元,異なる次元
    static Stream<Arguments> testConstructorProvider() {
        //@formatter:off
        return Stream.of(
                Arguments.of(null, new NullPointerException(), 0),
                Arguments.of(Collections.emptyList(), null, 0),
                Arguments.of(Arrays.asList(Arrays.asList(1.5, -2.1)), null, 2),
                Arguments.of(Arrays.asList(Arrays.asList(1.2, 0.1), Arrays.asList(0.0, 1.5)), null, 2),
                Arguments.of(Arrays.asList(null, Arrays.asList(0, 1.5), Arrays.asList(-0.9, 0.1)), new NullPointerException(), 0),
                Arguments.of(Arrays.asList(Arrays.asList(-0.9, 0.1), Arrays.asList(0.0, 1.5), Collections.emptyList()), new DimensionNotUnifiedException(), 0),
                Arguments.of(Arrays.asList(Collections.emptyList(), Collections.emptyList(), Collections.emptyList()), null, 0),
                Arguments.of(Arrays.asList(Arrays.asList(1.5), Arrays.asList(0.0), Arrays.asList(-2.2)), null, 1),
                Arguments.of(Arrays.asList(Arrays.asList(1.5, 2.2, -1.9), Arrays.asList(0.0, 0.0, 0.0), Arrays.asList(0.9, 5.0, 2.2)), null, 3),
                Arguments.of(Arrays.asList(Arrays.asList(1.5, null, -1.9), Arrays.asList(0.0, 0.0, 0.0), Arrays.asList(0.9, 5.0, 2.2)), new NullCoordinateException(), 0),
                Arguments.of(Arrays.asList(Arrays.asList(1.5, 2.1, -1.9), Arrays.asList(0.0, 0.0), Arrays.asList(0.9, 5.0, 2.2)), new DimensionNotUnifiedException(), 0),
                Arguments.of(Arrays.asList(Arrays.asList(2.1, -1.9), Arrays.asList(0, 0, 0), Arrays.asList(0.9, 5.0, 2.2)), new DimensionNotUnifiedException(), 0)
        );
        //@formatter:on
    }

    @ParameterizedTest
    @MethodSource("testConstructorProvider")
    @DisplayName("コンストラクタのテスト")
    void testConstructor(List<List<Double>> points, RuntimeException e, int dimension) {
        if (e == null) {
            Assertions.assertDoesNotThrow(() -> new EuclideanSpace(points));

            EuclideanSpace actual = new EuclideanSpace(points);
            Assertions.assertEquals(dimension, actual.getDimension());
        } else {
            Assertions.assertThrows(e.getClass(), () -> new EuclideanSpace(points));
        }
    }

    // points : 0件/1件/2件, 0次元/1次元/2次元, 0/正/負
    // target : null/空/1次元/2次元, null含む/含まない, 0/正/負/同一座標
    static Stream<Arguments> testDistanceFromTargetProvider() {
        return Stream.of(
                //@formatter:off
                Arguments.of(Collections.emptyList(), Collections.emptyList(), null, Collections.emptyList()),
                Arguments.of(Collections.emptyList(), Arrays.asList(0.1), new DimensionNotUnifiedException(), Collections.emptyList()),
                Arguments.of(Arrays.asList(Collections.emptyList()), Collections.emptyList(), null, Arrays.asList(0.0)),
                Arguments.of(Arrays.asList(Collections.emptyList()), Arrays.asList(0.1), new DimensionNotUnifiedException(), Collections.emptyList()),
                Arguments.of(Arrays.asList(Arrays.asList(3.0)), Arrays.asList(1.0), null, Arrays.asList(2.0)),
                Arguments.of(Arrays.asList(Arrays.asList(3.0)), Arrays.asList(1.0, 2.0), new DimensionNotUnifiedException(), Collections.emptyList()),
                Arguments.of(Arrays.asList(Arrays.asList(-1.0, 0.0)), Arrays.asList(2.0, -4.0), null, Arrays.asList(5.0)),
                Arguments.of(Arrays.asList(Arrays.asList(-1.0, 0.0)), Arrays.asList(null, -4.0), new NullCoordinateException(), Collections.emptyList()),
                Arguments.of(Arrays.asList(Arrays.asList(-3.0, 0.0), Arrays.asList(0.0, -4.0)), Arrays.asList(0.0, -4.0), null, Arrays.asList(5.0, 0.0))
                //@formatter:on
        );
    }

    @ParameterizedTest
    @MethodSource("testDistanceFromTargetProvider")
    @DisplayName("距離算出のテスト")
    void testDistanceFromTarget(List<List<Double>> points, List<Double> target, RuntimeException e, List<Double> distances) {
        EuclideanSpace space = new EuclideanSpace(points);

        if (e == null) {
            Assertions.assertEquals(distances, space.distanceFromTarget(target));
        } else {
            Assertions.assertThrows(e.getClass(), () -> space.distanceFromTarget(target));
        }
    }
}

今回実装したバージョンはGitHubのこちらのバージョンで公開しています。
https://github.com/tan3nonsugar/clusteringsample/releases/tag/v0.0.2

ここまで読んでいただいてありがとうございました。次回は「データの重心」という考え方についてお話ししようと思います。では～ノシ

  1. 厳密な話をすれば、非類似度/類似度の説明を先にしたり、距離の数学的な定義を満たす満たさないの話をするべきなのでしょうが、感覚をつかむことを優先してここでは割愛します。 ↩

2
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
1