はじめに
こんにちは、炭山水です。
前回の続きです。
【コンピューターサイエンス入門第2回:機械学習やってみる】 k平均法をJavaで実装してみよう~データ同士の距離~
もし、はじめましてでしたら、ぜひシリーズの最初からご覧いただければと思います。
【コンピューターサイエンス入門第0回:機械学習やってみる】 k平均法をJavaで実装してみよう
今回は「データ集合の中心」という考え方についてお話していきます。
環境
- IntelliJ IDEA
- Java12 + SpringBoot 2.1.6
- JUnit5
この環境の準備についてはこちらの記事で書きました。
IntelliJ+Gradle+SpringBoot+JUnit5(jupiter)で新規開発を始めるときの備忘録
やりたいこと
「なんでそんな考え方が必要なの?」という話はもう少し先に語るとして、どんなことをできるようにしておきたいかだけ先にお話ししておきます。
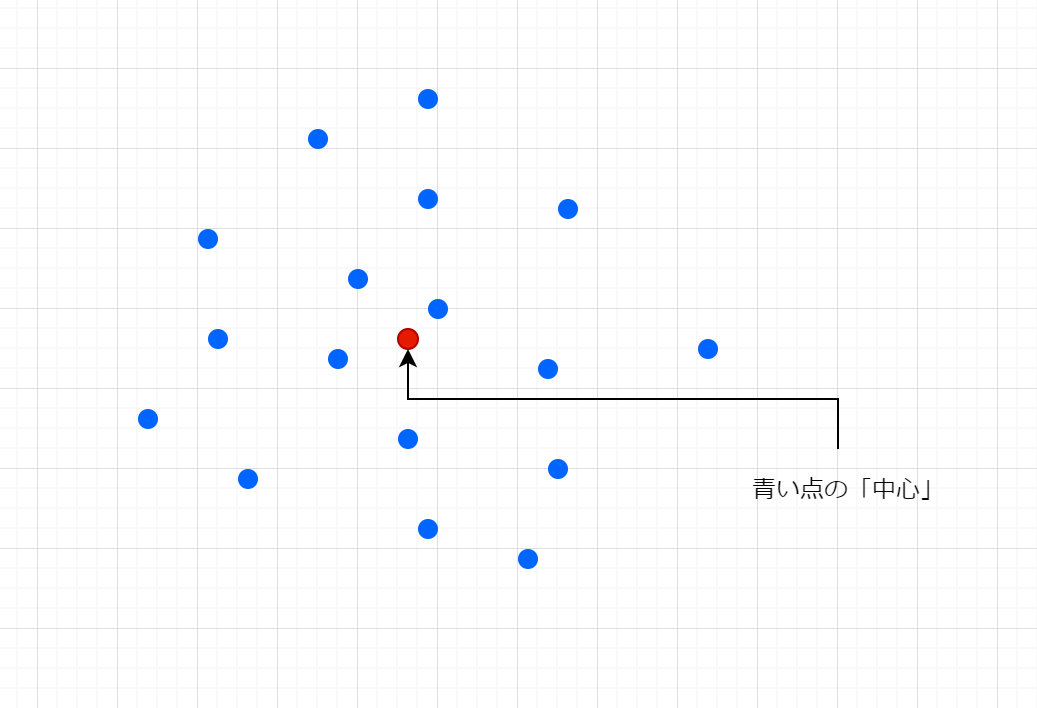
言葉で説明するより図を見てもらった方が早いのでこちらご覧ください。
こんな感じで、青い点のように複数のデータがあったとして、このグループの中心ってどこ?を定義しておきたいと思います。
第0回でもそんな話をしましたが、人間が見れば「だいたいこの辺だろう」と判断できますが、コンピュータには数字で計算できるように定義を与えてあげないといけません。
中心の算出方法
長々と御託を垂れましたが、ここは日常生活でもなじみのある**算術平均(相加平均)**を使います。1
「数学の平均点」とかで使うやつですね。全員分を合計して人数で割るアレです。
| 氏名 | 数学の点数 |
|---|---|
| Aさん | 70点 |
| Bさん | 60点 |
| Cさん | 90点 |
| Dさん | 50点 |
この場合、平均点は
(70+60+90+50)/4 = 67.5
つまり67.5点となりますね。
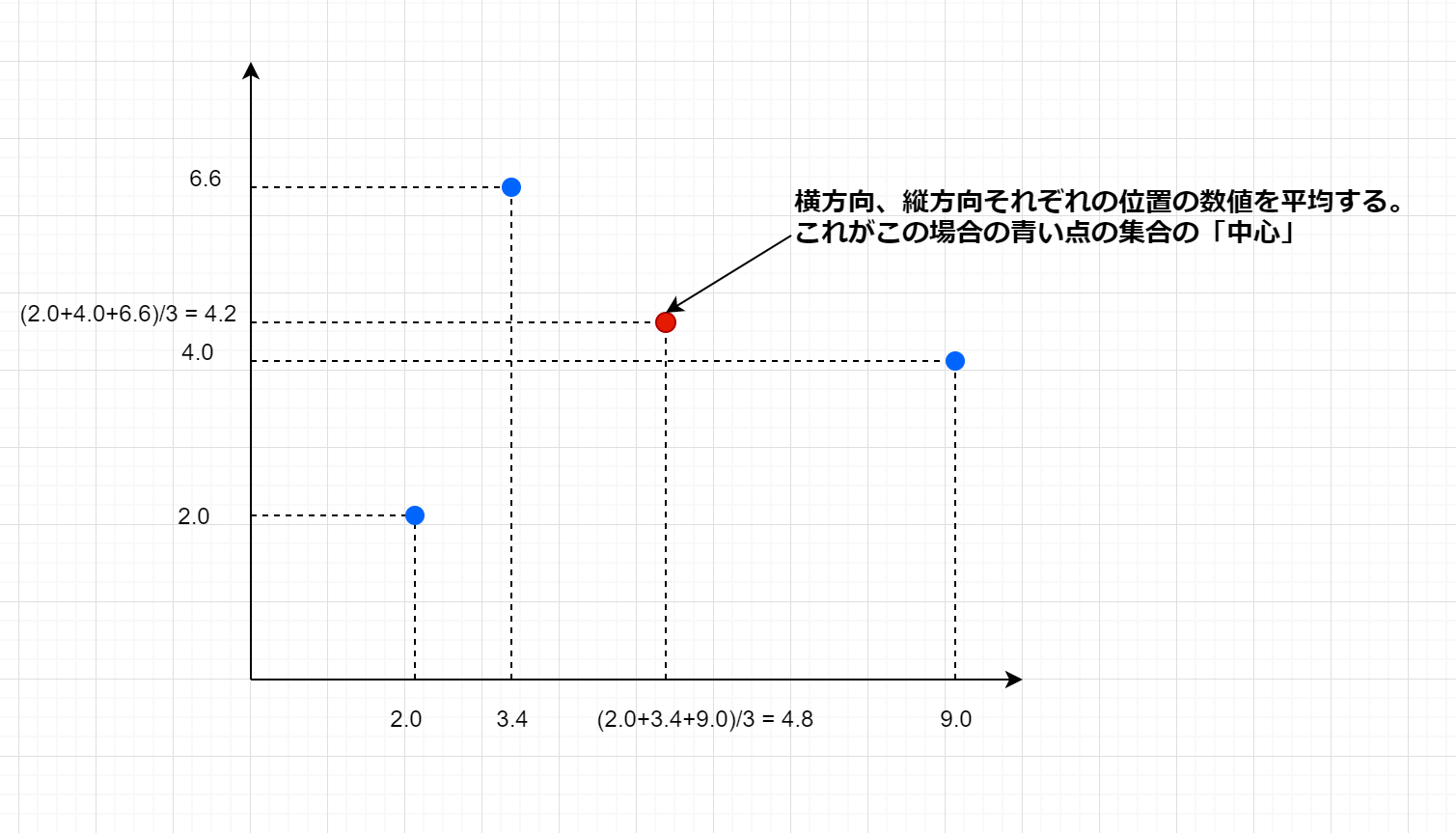
この考え方を座標の数値にも適用していきます。2次元のデータで考えると図のようになります。横方向と縦方向の数字をそれぞれ平均したものが「中心の座標」になります。
実装してみます
これまで作ってきたクラスに、getCentroidメソッドを追加しました。
package net.tan3sugarless.clusteringsample.lib.data;
import lombok.EqualsAndHashCode;
import lombok.Getter;
import lombok.ToString;
import lombok.Value;
import net.tan3sugarless.clusteringsample.exception.DimensionNotUnifiedException;
import net.tan3sugarless.clusteringsample.exception.NullCoordinateException;
import net.tan3sugarless.clusteringsample.exception.UnexpectedCentroidException;
import java.util.List;
import java.util.Objects;
import java.util.stream.Collectors;
import java.util.stream.IntStream;
/**
* ユークリッド距離空間上の座標集合
*/
@Getter
@ToString
@EqualsAndHashCode
@Value
public class EuclideanSpace {
private final List<List<Double>> points;
private final int dimension;
//
// ~~中略~~
//
/**
* インスタンスに所属する各点の中心点となる座標を求める
* <p>
* 中心は算術平均とする
*
* <pre>
* n次元空間において、i番,(x11+x21+....+xm1)/m,目の点のj番目の要素をxijとして、 *
* [x11, x12,...,x1n],[x21, x22,...,x2n]
* とm個の点が与えられているとき、中心点の座標は、
*
* [(x11+x21+....+xm1)/m,(x12+x22+....+xm2)/m,...,(x1n+x2n+....+xmn)/m]
* となる。
*
* という計算を行う。
* </pre>
*
* @return 中心点の座標
* @throws UnexpectedCentroidException 基本あり得ない
*/
public List<Double> getCentroid() {
return IntStream
.range(0, dimension)
.boxed()
.map(i -> points.stream().mapToDouble(point -> point.get(i)).average().orElseThrow(UnexpectedCentroidException::new))
.collect(Collectors.toList());
}
}
そしてテスト
/**
* points : 0次元/2次元 x 3要素
*/
static Stream<Arguments> testGetCentroidProvider() {
return Stream.of(
//@formatter:off
Arguments.of(Collections.emptyList(), Collections.emptyList()),
Arguments.of(asList(Collections.emptyList(), Collections.emptyList(), Collections.emptyList()), Collections.emptyList()),
Arguments.of(asList(asList(2.0, -4.0), asList(1.0, 0.0), asList(6.0, 1.0)), asList(3.0, -1.0))
//@formatter:on
);
}
@ParameterizedTest
@MethodSource("testGetCentroidProvider")
@DisplayName("中心算出のテスト")
void testGetCentroid(List<List<Double>> points, List<Double> centroid) {
EuclideanSpace space = new EuclideanSpace(points);
Assertions.assertEquals(centroid, space.getCentroid());
}
次回へ続く
今日はここまで。これで部品はそろったので、次回はいよいよk-平均法のメインロジックを解説していきます。
今回解説したバージョンはtagでgithubに残しておきましたのでよかったらご覧ください。
https://github.com/tan3nonsugar/clusteringsample/releases/tag/v0.0.3
-
「真ん中」の定義にはほかにも中央値など種類がありますが、話が散らかるので算術平均に話を固定しています。 ↩