はじめに
こんにちは。株式会社エイアイ・フィールドでプロダクト開発をしている久保です。この記事はエイアイ・フィールドアドベントカレンダー2021の20日目の記事です。今までこのアドベントカレンダーで多腕バンディット問題のアルゴリズムの紹介を行ってきました。
今回はこれらのアルゴリズムの比較を行います。今回の実験状況下ではありますが、結果をまとめると
- 実装時間があまりなく、コインの枚数も少ない時はepsilon greedy
- 無難に行くのであれば、UCB1
- コインの枚数が多く、少しでも改善をしたいのであれば、DMED
になります。
問題設定
初回に問題設定を行いましたが、せっかくなのでもう一度問題設定を行います。
今、あなたはカジノに来ています。このカジノでは専用のコインを買い、そのコインをつかってスロットマシンで遊びます。スロットマシンからは当たれば現金が1万円出てくるものとします。(スロットマシンから出たコインではスロットマシンは起動できないものとします)。
さて、さっそくあなたはコインを100枚入手しました。

このコインをつかって、スロットマシンに挑みます。このカジノには3台のスロットマシンがあり、それぞれ当たる確率が異なることがわかっています。
さて、どのようにプレーをすれば最終的な獲得金額を最大化できるでしょうか?
実験概要
この問題について、数値実験を用いて検証を行いますが、実験をするに際して、「それぞれのスロットマシンはベルヌーイ過程に従い、それぞれのスロットマシンの期待値は、0.3, 0.5, 0.8とします。」
これらは実験をするのに必要であり今回設定を行いますが、実際にプレーするときプレーヤーはこのことを知りようがないということに注意が必要です。
統計学の議論ではしばしばこのような、実験する主体には実験前には(あるいは実験後であっても)知りようのないことを設定することを求められます。この種の設定はよくモデルと呼ばれますが、私は個人的にこの知りようのないことを実験者(人間)の視点と対比して神様視点と呼びます。
設定している数値が人間視点なのか神様視点なのかを常に考えることが大事です。今回で言うと、実験結果やスロットマシンが3台あること、コインが100枚あることが人間視点で、スロットマシンがベルヌーイ過程に従い、それぞれの期待値が0.3, 0.5, 0.8であることが神様視点です1。
これらの設定の下、コインの枚数を増やしながらどのように値が変化するかを調べました。
以下、実験に使ったコードです。
import random
import math
import pandas as pd
# divergenceの計算
def b_divergence(p, q):
if q == 0:
if p == 0:
return 0
return 100_000_000
if q == 1:
if p == 1:
return 0
return 100_000_000
if p == 0:
return - math.log(1-q)
if p == 1:
return - math.log(q)
return p * math.log(p/q) + (1-p) * math.log((1-p)/(1 - q))
# 場の準備
class PlayBoard:
def __init__(self, machines=[], n_machines=3, n_coins=100):
if machines == []:
self.reset_machines(n_machines)
else:
self.set_machines(machines)
self.reset_history(n_coins)
def reset_machines(self, n_machines):
self.n_machines = n_machines
self.machine_mu = [random.random() for _ in range(self.n_machines)]
def set_machines(self, machine_mu):
self.n_machines = len(machine_mu)
self.machine_mu = machine_mu
def reset_history(self, n_coins):
self.n_coins = n_coins
self.reward = 0
self.score_board = ScoreBoard(len(self.machine_mu))
self.history = []
def play(self, arm, detail=True, hist_=True):
if self.n_coins < 1:
return
self.n_coins -= 1
reward = int( random.random() < self.machine_mu[arm])
self.record(arm, reward, detail=detail, hist_=hist_)
return self.n_coins == 0
def record(self, arm, reward, detail=True, hist_=True):
self.reward += reward
if detail:
self.score_board.count += 1
score = self.score_board.get_score(arm)
score.n_tries += 1
score.reward += reward
if hist_:
self.history.append({'count': self.score_board.count, 'reward': self.reward})
class Score:
def __init__(self, arm):
self.arm = arm
self.n_tries = 0
self.reward = 0
def get_ucb_score(self, count):
if self.n_tries == 0:
return 100_000_000
return self.reward / self.n_tries + math.sqrt(math.log(count) / 2 / self.n_tries)
def get_mu_hat(self):
if self.n_tries == 0:
return 100_000_000
return self.reward / self.n_tries
class ScoreBoard:
def __init__(self, n_scores):
self.scores = [Score(arm) for arm in range(n_scores)]
self.count = 0
def get_score(self, arm):
return self.scores[arm]
def select_arm_by(self, scoring):
if scoring == 'ucb':
res_ = [
{'arm': score.arm, 'score': score.get_ucb_score(self.count)}
for score in self.scores
]
elif scoring == 'mu_hat':
res_ = [
{'arm': score.arm, 'score':score.get_mu_hat()}
for score in self.scores
]
max_arm = max(res_, key=lambda x: x['score'])
return max_arm['arm']
def get_max_mu_hat(self):
return max([score.get_mu_hat() for score in self.scores])
def judge_dmed(self, arm):
score = self.get_score(arm)
return score.n_tries * b_divergence(score.get_mu_hat(), self.get_max_mu_hat()) <= math.log(self.count)
# アルゴリズムたち
def epsilon_greedy(pb, eps = 0.3):
n_exploration = int(eps * pb.n_coins)
n_exploitation = pb.n_coins - n_exploration
for idx in range(n_exploration):
pb.play(idx % pb.n_machines, hist_=False)
max_arm =pb.score_board.select_arm_by('mu_hat')
for _ in range(n_exploitation):
pb.play(max_arm, detail=False)
return pb.reward
def ucb1(pb):
n_coins = pb.n_coins
ended = False
for arm in range(pb.n_machines):
ended = pb.play(arm)
if ended:
break
while not ended:
arm_ = pb.score_board.select_arm_by('ucb')
ended = pb.play(arm_)
return pb.reward
def dmed(pb):
n_coins = pb.n_coins
ended = False
for arm in range(pb.n_machines):
ended = pb.play(arm)
if ended:
break
this_loop = [arm for arm in range(pb.n_machines)]
next_loop = []
while not ended:
for arm in this_loop:
ended = pb.play(arm)
if ended:
break
for arm_ in range(pb.n_machines):
if arm_ in next_loop:
continue
if pb.score_board.judge_dmed(arm_):
next_loop.append(arm_)
this_loop = next_loop
next_loop = []
return pb.reward
# 実験コード
def exam(method, n_tries=100, n_coins=100):
result = None
for idx in range(n_tries):
pb.reset_history(n_coins)
method(pb)
if result is None:
result = pd.DataFrame(pb.history)
else:
result = pd.concat([result, pd.DataFrame(pb.history)])
return result
def exam_eg(eps=0.3, n_tries=100, n_coins=100):
res_ = []
for idx in range(n_tries):
print(idx)
for jdx in range(n_coins):
pb.reset_history(jdx)
res = epsilon_greedy(pb, eps=eps)
res_.append({'count': jdx, 'reward': res})
return pd.DataFrame(res_)
実験結果
まず、場を準備し次のコードを実行しました。
pb = PlayBoard([0.3, 0.5, 0.8])
n_tries = 300
n_coins = 5000
df_eg = exam(epsilon_greedy, n_tries=n_tries, n_coins=n_coins)
ax_1 = df_eg.plot.scatter(x='count', y='reward', s=0.1, figsize=(30, 16), label='epsilon greedy')
df_ucb = exam(ucb1, n_tries=n_tries, n_coins=n_coins)
df_ucb.plot.scatter(x='count', y='reward', s=0.1, c='orange', figsize=(30, 16), ax=ax_1, label='ucb1')
df_dmed = exam(dmed, n_tries=n_tries, n_coins=n_coins)
df_dmed.plot.scatter(x='count', y='reward', s=0.1, c='green', figsize=(30, 16), ax=ax_1, label='dmed')
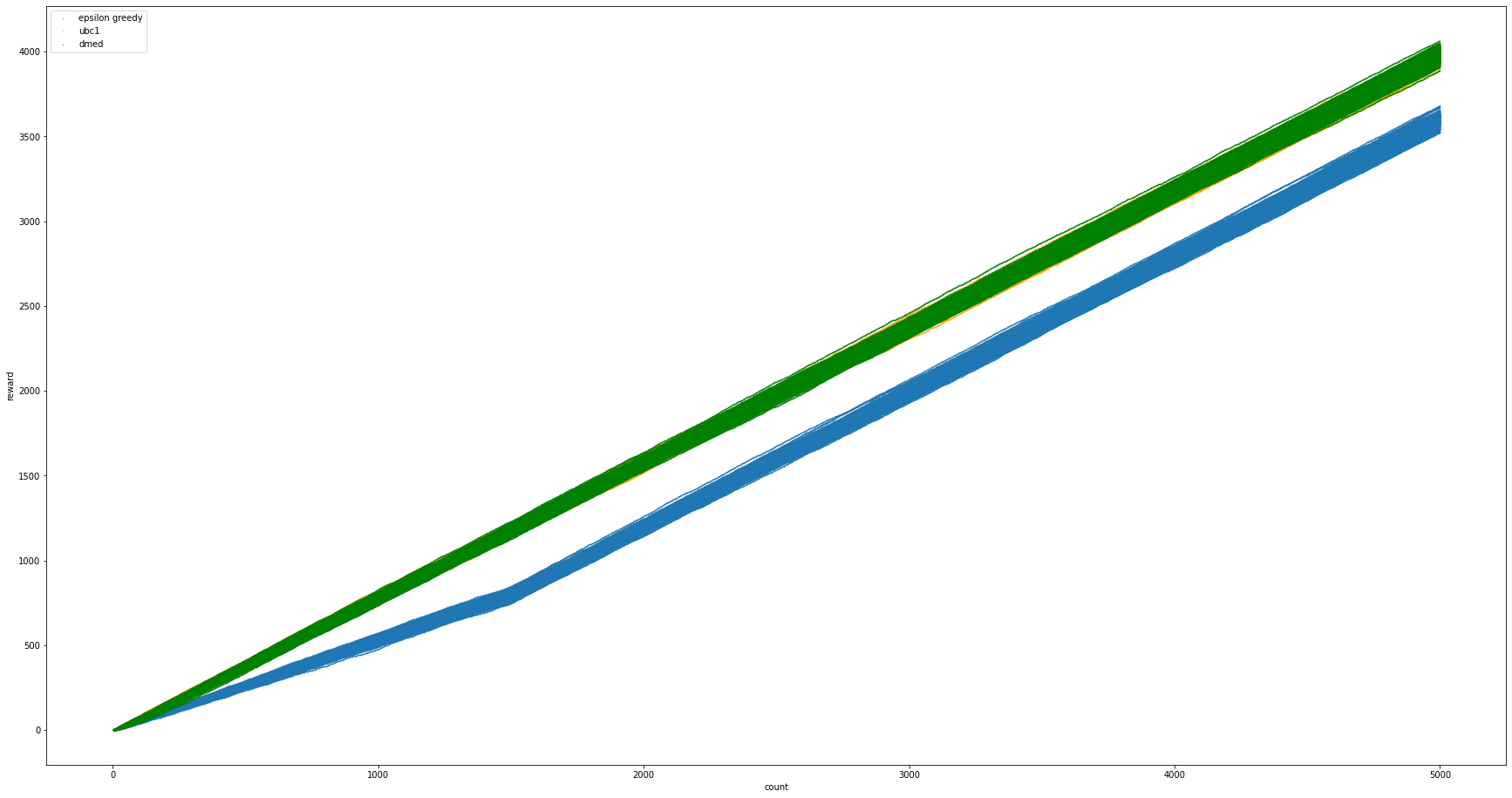
これは、コインを5000回使ったときの報酬の増加を表しています。それぞれのアルゴリズムを300回ずつ行いそれを表示してあります。epsilon greedy が青色、UCB1 がオレンジ色、DMED が緑色です。見てわかる通り、オレンジが見えません。これは緑色がオレンジ色と同じような動きをして上書きをしているからです。また、epsilon greedyが下回っているのがわかります。
しかし、ここで少し考えると、epsilon greedyは全体の何割かを先に探索に充てるので、この図による比較はフェアではないことがわかります。例えば、コインが100枚だった時、UCBやDMEDはこの図の通りに読めばよいのですが、epsilon greedyはこの図の中では探索中であり、この通りに読んではいけません。この点も踏まえて比較できるように、次のコードを実行しました。
df_eg_2 = exam_eg(n_tries=n_tries, n_coins=n_coins)
ax_1 = df_eg_2.plot.scatter(x='count', y='reward', s=0.1, figsize=(30, 16), label='epsilon greedy')
df_ucb.plot.scatter(x='count', y='reward', s=0.1, c='orange', figsize=(30, 16), ax=ax_1, label='ucb1')
df_dmed.plot.scatter(x='count', y='reward', s=0.1, c='green', figsize=(30, 16), ax=ax_1, label='dmed')
注意
このコードをGoogle Colab上で実行すると80分程度かかります。
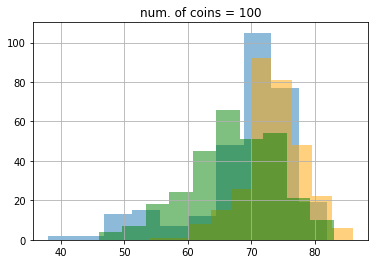
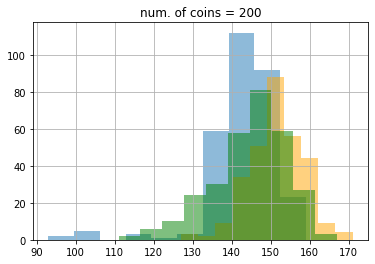
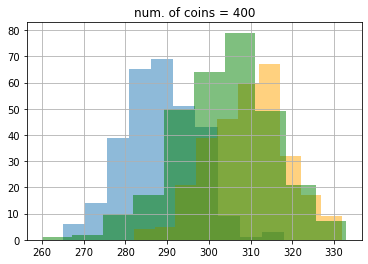
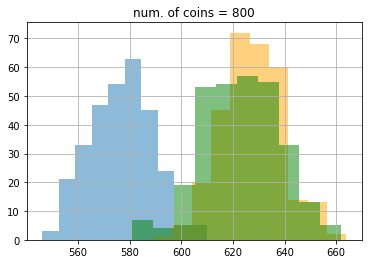
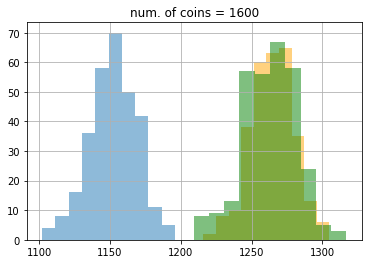
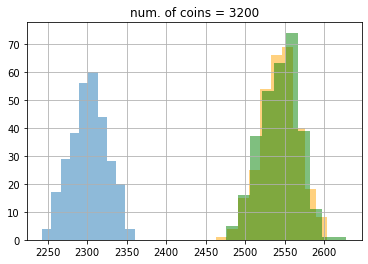
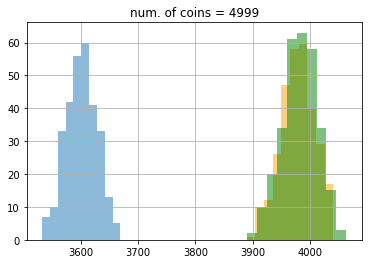
結果はこのようになりました。この図ではわかりにくいので、ヒストグラムでコインが100, 200, 400, 800, 1600, 3200, 4999枚の時をプロットしてみましょう。
コードは以下の通りです。
import matplotlib.pyplot as plt
data = []
for count_point in [100, 200, 400, 800, 1600, 3200, 4999]:
ax_2=df_eg_2.query('count == @count_point').reward.hist(alpha=.5)
df_ucb.query('count == @count_point').reward.hist(alpha=.5, color='orange', ax=ax_2)
df_dmed.query('count == @count_point').reward.hist(alpha=.5, color='green', ax=ax_2)
ax_2.set_title(f'num. of coins = {count_point}')
plt.show()
ax_2.clear()
data.append({
'count': count_point,
'esp_greed': df_eg_2.query('count == @count_point').reward.mean(),
'ucb': df_ucb.query('count == @count_point').reward.mean(),
'dmed': df_dmed.query('count == @count_point').reward.mean()
})
df_mean = pd.DataFrame(data)
結果は次のようになりました。ここでもepsilon greedy が青色、UCB1 がオレンジ色、DMED が緑色です。
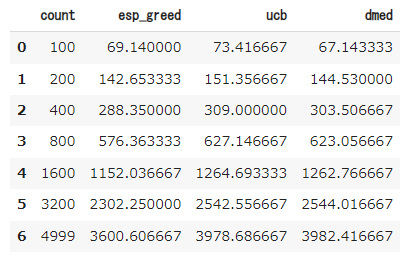
期待値もこのようになりました。
最初100枚のときはDMEDはepsilon greedyにも負けていたのが、最終的に3200枚のあたりでUCB1にも勝っていることがわかります。ここで、5000枚使った時の理想的な手を選び続けたときの平均値は0.8 * 5000 = 4000なので、epsilon greedyは約400、UCBは約22、DMEDは約18改善の余地があることがわかります。なかなかこれ以上の改善は難しいですが、試してみるのも面白いかもしれません(DMEDより良いといわれている手法にIMEDなどがあります)。
これらの結果から、今回の設定、つまり3つのスロットマシンでその平均値が0.3, 0.5, 0.8の状況では、
- 実装時間があまりなく、コインの枚数も少ない時はepsilon greedy
- 無難に行くのであれば、UCB1
- コインの枚数が多く、少しでも改善をしたいのであれば、DMED
となるのではないでしょうか。
おわりに
今回は多腕バンディット問題のアルゴリズムの比較を行いました。初回にも書いた通り、多腕バンディット問題はこのようなスロットマシンの問題だけでなく、もう少し問題を拡張することによって広告配信や推薦、囲碁などのゲーム木探索などにも応用されているます。また、問題の形式を少し変えることによって、デザインにおけるA/Bテストの世界ともつながっていきます。
日本語では本多さんの本がお勧めなのでぜひ読んでみてください。
これまで4回にわたる多腕バンディット問題の入門的な記事も今回で終わりです。ここまでお読みいただきありがとうございました。また機会があれば今度は線形バンディットやその応用である文脈付きバンディットについて書いてみたいと思います。それでは次の機会に。
-
「神様なら実験結果とかも含めて全部知っているだろう」と考えるのであれば、胴元視点と言ってもよいです。 ↩