はじめに
教師なし学習は一般的に教師あり学習と比較すると精度が落ちますが、その代わりに様々なメリットがあります。具体的に教師なし学習が役に立つシーンとして
**- パターンがあまりわかっていないデータ
- 時間的に変動するデータ
- 十分にラベルがついていないデータ**
などが挙げられます。
教師なし学習ではデータそのものから、データの背後にある構造を学習します。これによってラベルのついていないデータをより多く活用できるので、新たなアプリケーションへの道が開けるかもしれません。
この記事では、mnistのデータを教師なし学習により分類の実装例を紹介します。
手法は主成分分析とt-SNE、k-means法を用います。
続編の記事では、オートエンコーダを用いた分類にもチャレンジしてみたいと考えています。
この記事でやること
**- mnistデータを教師なし学習で分類
- PCA + k-means法による分類の実装と評価
- PCA+t-SNE + k-means法による分類の実装と評価**
ライブラリのインポート
import random
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.metrics import confusion_matrix
from sklearn.manifold import TSNE
データの準備
mnist = keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# 正規化
train_images = (train_images - train_images.min()) / (train_images.max() - train_images.min())
test_images = (test_images - test_images.min()) / (test_images.max() - test_images.min())
train_images.shape,test_images.shape
一応可視化します。見覚えのある数字たちですね。
# ランダムに可視化
fig, ax = plt.subplots(4,5,figsize=[8,6])
ax_f = ax.flatten()
for ax_i in ax_f:
idx = random.choice(range(train_images.shape[0]))
ax_i.imshow(train_images[idx,:,:])
ax_i.grid(False)
ax_i.tick_params(labelbottom=False,labelleft=False)
主成分分析による画像の分類
mnistのデータは28*28=784次元のデータとなっています。このくらいであればぎりぎりそのままでもk-means法を適用することができそうですが、分類する前に次元削減をするのが有効です。そうすることで、計算量をへらすことが可能です。
次元削減の手法として主成分分析(PCA)を用います。そしてPCAで次元削減されたデータに対して、k-means法を適用してデータを分類していきます。
主成分分析の実行
df_train = pd.DataFrame(train_images.reshape(train_images.shape[0],28*28))
pca = PCA()
pca.fit(df_train)
feature = pca.transform(df_train)
# 二次元で可視化
plt.scatter(feature[:,0],feature[:,1],alpha=0.8,c=train_labels)
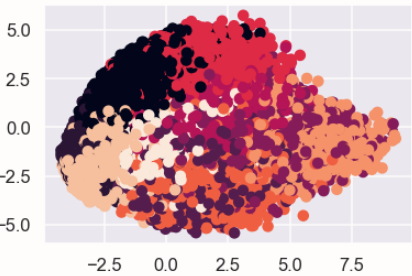
主成分の第一成分と第二成分で可視化した結果がこちらです。
0~9の10個のクラスタで色分けしています。
なんとなく分類できているようにも見えますが...かなり重なっている部分が多いですね。
次に、第何成分までを用いてk-meansを適用するかを考えていきます。
そのためにそれぞれの成分の寄与率を可視化します。
# 寄与率の変化
ev_ratio = pca.explained_variance_ratio_
ev_ratio = np.hstack([0,ev_ratio.cumsum()])
df_ratio = pd.DataFrame({"components":range(len(ev_ratio)), "ratio":ev_ratio})
plt.plot(ev_ratio)
plt.xlabel("components")
plt.ylabel("explained variance ratio")
plt.xlim([0,50])
plt.scatter(range(len(ev_ratio)),ev_ratio)
結果をみると第100成分までで90%以上のデータが復元できることがわかります。
いろいろ実験するとわかりますが、分類するときは10成分もあれば十分でした。(下に記す評価方法で実験しました)
このことから、第10成分までを用いてk-means法を適用して分類してみます。
次元数が少ないほど計算数が減るので、少ないほうが好ましいですね。
k-means法による分類
まずはk-means法を適用します。
クラスタが10個あることがわかっているので、まずは10個に分類してみます。
KM = KMeans(n_clusters = 10)
result = KM.fit(feature[:,:9])
分類結果の評価
まずは、分類結果を混同行列で表示します。
df_eval = pd.DataFrame(confusion_matrix(train_labels,result.labels_))
df_eval.columns = df_eval.idxmax()
df_eval = df_eval.sort_index(axis=1)
df_eval
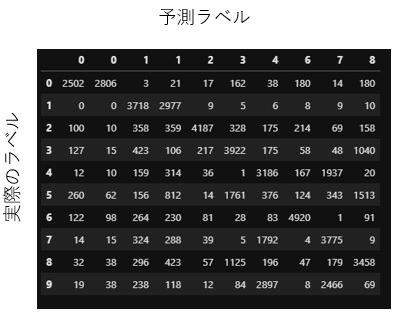
分類してクラスタの中で最も多かった正解ラベルのものを予測ラベルとしました。
例えば、クラスタNo.0に0が100個、1が20個、4が10個含まれていたらこれは0を予測している、といった具合ですね。
結果をみると、0と予測しているクラスタと1と予測しているクラスタが2つあることがわかりますね。
つまり主成分分析とk-means法では10個の数字に上手に分類するのは難しかったと考えられます。
それでは、いくつのクラスタに分類するのが最適なのかを考えていきます。
当たり前のことですが、クラスタ数が多ければクラスタの中は似たものが多くなりますが解釈が難しくなる。逆に少なければ、解釈は簡単ですがクラスタの中にいろんなデータが含まれることになります。
なので、クラスタ数は少ないけどできるだけ似たようなデータを含んだ分類がいいですね。
ここでは正解データがわかっているので、クラスタの中で最も多いラベルを正解ラベルとして、正解ラベルの数が最も多くなるようなクラスタ数を見つけたいと思います。
なので評価指標を、正解ラベルとなった数/全体の数とします。
# クラスタの中のデータの最も多いラベルを正解ラベルとしてそれが多くなるようなクラスタ数を探索
eval_acc_list=[]
for i in range(5,15):
KM = KMeans(n_clusters = i)
result = KM.fit(feature[:,:9])
df_eval = pd.DataFrame(confusion_matrix(train_labels,result.labels_))
eval_acc = df_eval.max().sum()/df_eval.sum().sum()
eval_acc_list.append(eval_acc)
plt.plot(range(5,15),eval_acc_list)
plt.xlabel("The number of cluster")
plt.ylabel("accuracy")
クラスタ数を5~15に変化させた場合の結果です。
クラスタ数が増えるほど同質性が増えており、accuracyが上がっていますね。
どこが最適か、というのは目的によりますが、クラスタ数10程度が解釈性を考えると良さそうです。
つまり、PCAのみでは10個のラベルにきれいにわけるのは難しいということになりました。
そこで、次はt-SNEという手法を組み合わせたいと思います。
PCA+t-SNEによる分類
t-SNEの実行
PCAのみでは10個に分類するのが難しかったので、PCAとt-SNEを組み合わせて分類をしてみます。
t-SNEは原理がなかなか難しそうな手法です(自分もよくわかっていない)。
詳しい解説があるサイトを参考文献に乗せておきます。
t-SNEは計算時間がかかる手法なので、PCAで次元削減した10次元の10000個のデータの分類を行います。
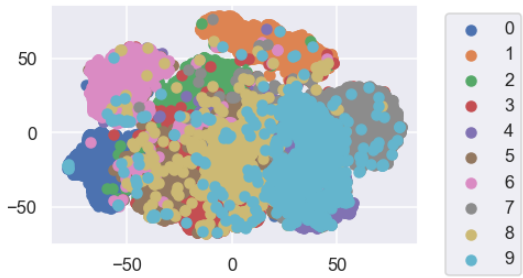
可視化するとまあまあいい感じに分類できていそうな気もします。
tsne = TSNE(n_components=2).fit_transform(feature[:10000,:9])
# 可視化
for i in range(10):
idx = np.where(train_labels[:10000]==i)
plt.scatter(tsne[idx,0],tsne[idx,1],label=i)
plt.legend(loc='upper left',bbox_to_anchor=(1.05,1))
k-meansによる分類と評価
つぎに、k-means法で分類して、混同行列を表示します。
# tsneしたものをkmeansで分類
KM = KMeans(n_clusters = 10)
result = KM.fit(tsne)
df_eval = pd.DataFrame(confusion_matrix(train_labels[:10000],result.labels_))
df_eval.columns = df_eval.idxmax()
df_eval = df_eval.sort_index(axis=1)
df_eval
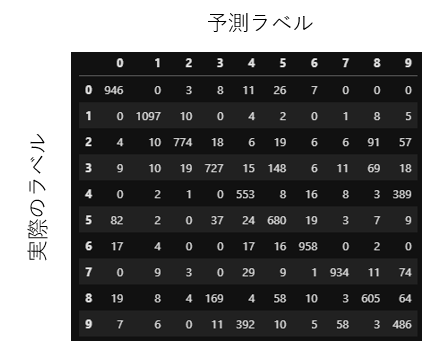
たまたまかもしれませんが、10個のラベルに上手に分かれています。良かったよかった。
この表をみていると、「4」と「9」を間違って分類していることが多いのがわかります。
実際にt-SNEの結果を可視化した散布図をみても4と9は近いところにありますね。
この学習方法では4と9が似ているものと学習していることがわかります。
なんで似てると考えているのかは不明ですが、なんだが面白いですね。
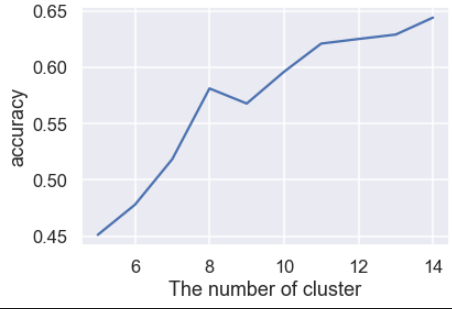
最後にクラスタ数ごとのaccuracyの評価を行います。
クラスタ数10のときaccuracyは0.6となっています。
PCAのみのときよりやや高い結果となっていますね。
# クラスタの中のデータの最も多いラベルを正解ラベルとしてそれが多くなるようなクラスタ数を探索
eval_acc_list=[]
for i in range(5,15):
KM = KMeans(n_clusters = i)
result = KM.fit(feature[:,:9])
df_eval = pd.DataFrame(confusion_matrix(train_labels,result.labels_))
eval_acc = df_eval.max().sum()/df_eval.sum().sum()
eval_acc_list.append(eval_acc)
plt.plot(range(5,15),eval_acc_list)
plt.xlabel("The number of cluster")
plt.ylabel("accuracy")
終わりに
mnistを題材としてPCAとt-SNEによる次元削減と可視化、k-meansによる分類と評価について実装しました。
ラベルのないデータは世の中に溢れているのでなかなか有用そうな手法です。
参考になりましたらLGTM等していただけると励みになります。
参考文献
t-SNE を用いた次元圧縮方法のご紹介
https://blog.albert2005.co.jp/2015/12/02/tsne/
t-SNEを理解して可視化力を高める
https://qiita.com/g-k/items/120f1cf85ff2ceae4aba