この記事でやること
- 映画のデータセットを用いた推薦システムを紹介
- 行列分解を用いた映画の評価予測システムの実装
はじめに
前回は教師なし学習を使ったオートエンコーダによる異常検知について紹介しました。
https://qiita.com/nakanakana12/items/f238b9760af2c62fa0e8
しかしこれらの方法はあくまで識別するのみで新しいデータを生成することはできません。
次は、 データを生成するモデルについて紹介していきます。
このようなモデルは、データセットの確率分布を学習して、見たことないデータに対して推測を行いたい場合もあります。
参考図書である「pythonによる教師なし学習」では映画の推薦システムが 例として挙げられていました。
今回の記事ではまず、広く用いられている手法であるらしい「行列分解による評価予測システム」について紹介します。
扱うデータ
扱うデータは映画の評価データセットです。MovieLens 20Mと呼ばれるもので、 20,000,000件ほどの評価で構成されています。データ全体だと200MBもあり重いので、1000件の格付けの多い映画と、1000人のランダムサンプルしたユーザのみのデータを扱います。
このとき格付け数は9万件となります。
扱ったデータはこちら
https://drive.google.com/file/d/1mXioVp1LiBQt1TJyE9IStCCpjijpb4SX/view?usp=sharing
元データはこちらからダウンロードできます。
https://grouplens.org/datasets/movielens/20m/
行列分解とは？
推薦システムでは協調フィルタリングシステムと呼ばれる方法が多く用いられます。これは似ているユーザーの挙動から推薦を行うシステムです。netflixなんかが有名です。
協調フィルタリングシステムと呼ばれる方法が多く用いられます。これは似ているユーザーの挙動から推薦を行うシステムです。
しかし協調フィルタリングシステムを行う時に、大量のデータが必要であったり似たような映画のアイテムの類似性を取られなかったりなどの問題点があります。
そこで用いられるのが行列分解による次元削減です。
ここでは超簡単に概要のみ紹介します。詳しい原理は参考記事を参照ください。
参考記事:Matrix Factorizationとレコメンドと私
https://qiita.com/michi_wkwk/items/52660778ad6a900965ee
行列分解では各ユーザーそして各映画の潜在因子をまず抜き出します。この潜在因子というのはつまり各ユーザーの特徴をベクトル化するということです。
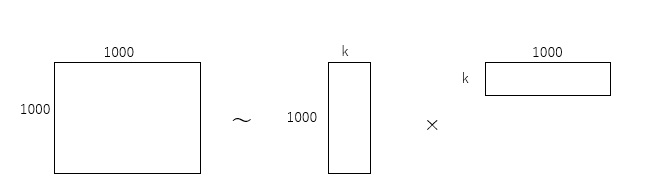
たとえばユーザーが1000個の映画を評価してたとしたらそのユーザーは1000個の行列で表されています。
この行列をぎゅっと圧縮して次元削減を行います。図にするとこんな感じ。図ではk列に圧縮しています。
この圧縮したデータから各ユーザ・アイテムの格付けを予測することで、少ないデータのみで予測することが可能になります。
ライブラリのインポート
まんま参考書籍のままです。
'''Main'''
import numpy as np
import pandas as pd
import os, time, re
import pickle, gzip, datetime
from datetime import datetime
'''Data Viz'''
import matplotlib.pyplot as plt
import seaborn as sns
color = sns.color_palette()
import matplotlib as mpl
%matplotlib inline
'''Data Prep and Model Evaluation'''
from sklearn import preprocessing as pp
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import log_loss
from sklearn.metrics import precision_recall_curve, average_precision_score
from sklearn.metrics import roc_curve, auc, roc_auc_score, mean_squared_error
'''Algos'''
import lightgbm as lgb
'''TensorFlow and Keras'''
# import tensorflow as tf
# import tensorflow as tf
import keras
from keras import backend as K
from keras.models import Sequential, Model
from keras.layers import Activation, Dense, Dropout
from keras.layers import BatchNormalization, Input, Lambda
from keras.layers import Embedding, Flatten, dot
from keras import regularizers
from keras.losses import mse, binary_crossentropy
sns.set("talk")
データの読み込みと確認
ratingDFX3 = pd.read_pickle(DATA_DIR + "data/datasets/movielens_data/ratingReducedPickle.pkl")
# 中身確認
n_users = ratingDFX3.userId.unique().shape[0]
n_movies = ratingDFX3.movieId.unique().shape[0]
n_ratings = len(ratingDFX3)
avg_ratings_per_user = n_ratings/n_users
print('Number of unique users: ', n_users)
print('Number of unique movies: ', n_movies)
print('Number of total ratings: ', n_ratings)
print('Average number of ratings per user: ', avg_ratings_per_user)
"""
Number of unique users: 1000
Number of unique movies: 1000
Number of total ratings: 90213
Average number of ratings per user: 90.213
"""
ratingDFX3.head()
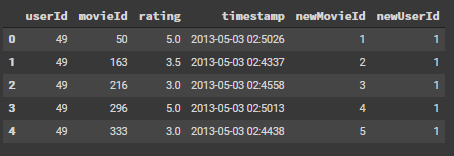
中身を確認するとこのように表示されます。
ratingが格付け、newMovieID、newUserIDがそれぞれ評価に用いるIDとなります。
# 訓練データと学習データの切り分け
X_train, X_test = train_test_split(ratingDFX3, test_size=0.10, \
shuffle=True, random_state=2018)
X_validation, X_test = train_test_split(X_test, test_size=0.50, \
shuffle=True, random_state=2018)
格付け行列の作成
まずはmovieID * userIDの行列を作成します。
各ユーザはごく一部の映画にしか格付けしていないため、殆どが0の行列となります。
更に検証データを一行にフラット化します。これを評価用の行列として用いることとします。
#格付け行列を作成する、ほとんどがゼロのスパース行列となる
ratings_train = np.zeros((n_users,n_movies))
for row in X_train.itertuples():
ratings_train[row[6]-1,row[5]-1] = row[3]
ratings_train.shape
#(1000,1000)
# 検証データの格付け行列
ratings_validation = np.zeros((n_users, n_movies))
for row in X_validation.itertuples():
ratings_validation[row[6]-1, row[5]-1] = row[3]
#検証データをフラット化
actual_validation = ratings_validation[ratings_validation.nonzero()].flatten()
ベースラインの設定
評価には予測した格付けと実際の格付けの二乗誤差二乗誤差を用います。
評価のベースラインとして
「すべてを3.5と予測したときの誤差はいくつか？」
ということを考えます。
#予測値を3.5としたときの二乗誤差(MSE)を検証セットに対して計算
#これをベースラインとする
pred_validation = np.zeros((len(X_validation),1))
pred_validation[pred_validation==0] = 3.5
print("3.5 MSE:",mean_squared_error(pred_validation,actual_validation))
#3.5 MSE: 1.055420084238528
1.055となりました。これが一旦のベースラインとなります。
果たして行列分解による推薦システムはこれを超えられるでしょうか。
行列分解による予測
#行列分解
#ユーザとアイテムの次元を減らして圧縮する
n_latent_factors = 3 #潜在因子、何次元に埋め込むか
#kerasで圧縮されたユーザ列の作成
user_input = Input(shape=[1], name="user")
user_embedding = Embedding(input_dim=n_users+1, output_dim=n_latent_factors,name="user_embedding")(user_input)
user_vec = Flatten(name="flatten_users")(user_embedding)
#kerasで圧縮された映画列の作成
movie_input = Input(shape=[1], name='movie')
movie_embedding = Embedding(input_dim=n_movies + 1, \
output_dim=n_latent_factors,
name='movie_embedding')(movie_input)
movie_vec = Flatten(name='flatten_movies')(movie_embedding)
product = dot([movie_vec, user_vec], axes=1)
model = Model(inputs=[user_input, movie_input], outputs=product)
model.compile('adam', 'mean_squared_error')
history = model.fit(x=[X_train.newUserId, X_train.newMovieId], \
y=X_train.rating, epochs=30, \
validation_data=([X_validation.newUserId, \
X_validation.newMovieId], X_validation.rating), \
verbose=1)
計算した結果を確認します。
pd.Series(history.history['val_loss'][10:]).plot(logy=False)
plt.xlabel("Epoch")
plt.ylabel("Validation Error")
print('Minimum MSE: ', min(history.history['val_loss']))
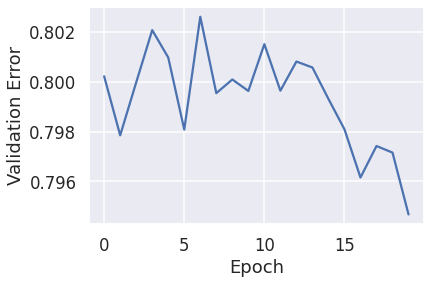
#Minimum MSE: 0.7946764826774597
行列分解を用いた場合だと0.794となりベースラインの1.055よりも小さい値となっています。
これより行列分解による評価予測システムはうまく機能していることがわかります。
実際にはこれを用いて、評価用ユーザの人たちがまだ評価していないけど評価の高そうな映画を提案していけば、推薦システムができそうです。
終わりに
今回は映画の推薦システムを題材とした場合の行列分解による評価予測システムを紹介しました。
しかし、教師なし学習の真の威力は
「教師なし生成モデル」
にあります。なんとか学習を続けてそこまでまとめて行きたいと思います。
参考記事
Matrix Factorizationとレコメンドと私
https://qiita.com/michi_wkwk/items/52660778ad6a900965ee