この記事でやったこと
**- kerasを使ってオートエンコーダの実装にチャレンジ
- 教師なし学習による異常検知を実装
- 再現率と適合率から効果を評価**
はじめに
教師なし学習は一般的に教師あり学習と比較すると精度が落ちますが、その代わりに様々なメリットがあります。具体的に教師なし学習が役に立つシーンとして
**- パターンがあまりわかっていないデータ
- 時間的に変動するデータ
- 十分にラベルがついていないデータ**
などが挙げられます。
教師なし学習ではデータそのものから、データの背後にある構造を学習します。これによってラベルのついていないデータをより多く活用できるので、新たなアプリケーションへの道が開けるかもしれません。
というわけで、今回は教師なし学習を使った異常検知の方法について紹介します。異常検知にも色々な種類がありますが、ここではオートエンコーダを用いたときの異常検知のコードを紹介します。
扱うデータ
クレジットカードの不正検知に関するデータセットを用います。元々はkaggleで用いられたデータみたいです。
下記よりデータがダウンロードできます。
https://github.com/aapatel09/handson-unsupervised-learning/blob/master/datasets/credit_card_data/credit_card.csv
ライブラリのインポート
参考図書のまんまなので、少し不要なものも含まれています。
'''Main'''
import numpy as np
import pandas as pd
import os, time, re
import pickle, gzip
'''Data Viz'''
import matplotlib.pyplot as plt
import seaborn as sns
color = sns.color_palette()
import matplotlib as mpl
%matplotlib inline
'''Data Prep and Model Evaluation'''
from sklearn import preprocessing as pp
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import log_loss
from sklearn.metrics import precision_recall_curve, average_precision_score
from sklearn.metrics import roc_curve, auc, roc_auc_score
'''TensorFlow and Keras'''
import tensorflow as tf
import keras
from keras import backend as K
from keras.models import Sequential, Model
from keras.layers import Activation, Dense, Dropout
from keras.layers import BatchNormalization, Input, Lambda
from keras import regularizers
from keras.losses import mse, binary_crossentropy
sns.set("talk")
データのダウンロード
data = pd.read_csv("credit_card.csv")
dataX = data.copy().drop(["Class","Time"],axis=1)
dataY = data["Class"].copy()
print("dataX shape:{},dataY shape:{}".format(dataX.shape,dataY.shape))
dataX.head()
こんな感じのデータ出力されると思います。実際には29列あるはず。

- dataXには284807人のカードの利用を表すデータが含まれている
- dataYには284807人の破産したかどうかのデータがある
ということになります。カードのどのような利用を表しているかなどはこのデータからだけではわかりまりませんね。
異常検知手法の概要
次にどうやって異常検知を行うかを紹介します。
上記のデータでは、利用者の約0.2%が不正利用されているということになっています。すなわち殆どが正常に使われているデータということになります。
そこで、この不正利用されているデータではなにがしかデータ構造が正常データと異なると考えます。このデータ構造の違いをオートエンコーダを使ってあぶり出してやろう、という試みです。
ではどうやってオートエンコーダで異常データを炙り出せるのでしょうか。オートエンコーダとは下記のように、一度次元数を落としたデータに圧縮したのちに、再び同じ次元数のデータに再構成します。
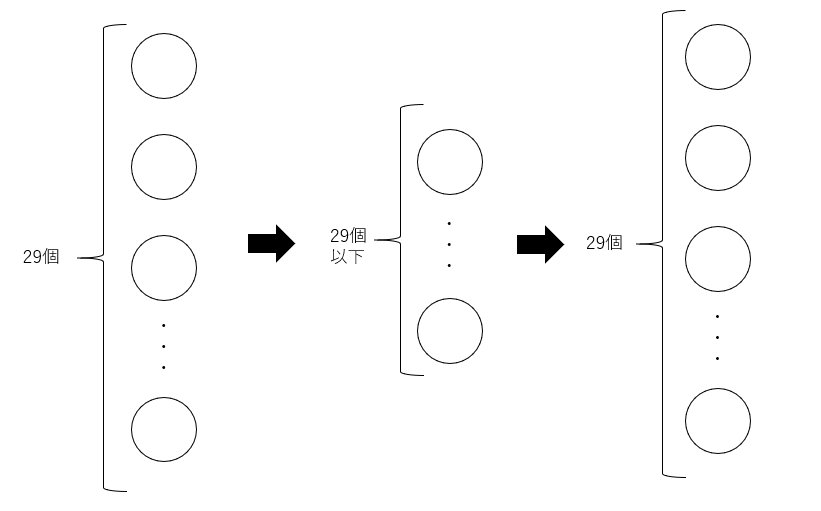
再構成されたデータでは、通常では元のデータと同じ値になっています。しかしながら、異常なデータでは通常のデータと異なり、元のデータとは異なるデータになります。
この元のデータと再構成されたデータの誤差をとってやることで異常データかどうかを判断します。
最初は自分はあまりすっきりしない方法でしたが、よくよく考えるとめちゃくちゃ合理的です。ただ、注意としてこの手法では異常データの数が通常データと比較して非常に少ないことが前提となっています。異常データがいっぱいあると、通常データの再構成もうまくいかなくなってしまうためです。
訓練データと評価データの作成
# 全ての特徴量の平均が0、標準偏差が1となるようにスケール変換する
featuresToScale = dataX.columns
sX = pp.StandardScaler(copy=True, with_mean=True, with_std=True)
dataX.loc[:,featuresToScale] = sX.fit_transform(dataX[featuresToScale])
# 訓練データとテストデータに振り分ける
X_train, X_test, y_train, y_test = \
train_test_split(dataX,dataY,test_size=0.33,random_state=2018,stratify=dataY)
X_train_AE = X_train.copy()
X_test_AE = X_test.copy()
オートエンコーダの実装
次にオートエンコーダの実装方法です。
ここでは2層の線形活性化関数を用いたオートエンコーダを作成します。
普段と違うのは正解データを用いないので、正解データも学習データと同じものを入力しているところですね。
# 2層の線形活性化関数を用いたオートエンコーダの構築
model = Sequential()
model.add(Dense(units=27,activation="linear",input_dim=29)) #unitsでいくつの層にデータを凝縮するかを決定する。
model.add(Dense(units=29,activation="linear"))
model.compile(optimizer="adam",loss="mean_squared_error",metrics="accuracy")
num_epochs = 3
batch_size = 32
history = model.fit(x=X_train_AE,y=X_train_AE,
epochs=num_epochs,
batch_size=batch_size,
shuffle=True,
validation_data=(X_train_AE,X_train_AE),
verbose=1)
評価関数の作成
ここまでで、オートエンコーダができました。次に、このオートエンコーダを評価するために
**- 元のデータと最高性されたデータの誤差を計算する関数
- 適合率-再現率曲線、AUC曲線を描画する関数**
を作成します。
まずは、再構成誤差を計算する関数です。こちらは二乗誤差をとるだけなのでそこまで難しくはなさそうです。
# 元の特徴量と新たに再構成された特徴量行列の間の最高性誤差を計算する異常スコア関数
# 二乗誤差の和を計算して正規化し、0と1の間にする
# 1に近いと異常、0に近いと正常
def anomalyScores(originalDF,reduceDF):
loss = np.sum((np.array(originalDF)-np.array(reduceDF))**2,axis=1)
loss = pd.Series(data=loss,index=originalDF.index)
loss = (loss-np.min(loss))/(np.max(loss)-np.min(loss))
return loss
次に適合率-再現率曲線、AUC曲線を描画する関数です。
# 適合率-再現率曲線、平均適合率、auROC曲線をプロットする
def plotResults(trueLabels, anomalyScores,returnPreds=False):
preds = pd.concat([trueLabels,anomalyScores],axis=1)
preds.columns = ["trueLabel","anomalyScore"]
#各しきい値のときの適合率(precision)と再現率(recall)を計算
precision, recall, thresholds = precision_recall_curve(preds["trueLabel"],preds["anomalyScore"])
average_precision = average_precision_score(preds["trueLabel"],preds["anomalyScore"])
# 適合率-再現率曲線
plt.step(recall,precision,color="k",alpha=0.7,where="post")
plt.fill_between(recall,precision,step="post",alpha=0.3,color="k")
plt.xlabel("Recall")
plt.ylabel("Precision")
plt.ylim([0,1.05])
plt.xlim([0,1.0])
plt.title("Precision-Recall Curve:Average Precision={0:0.2f}".format(average_precision))
fpr,tpr,thresholds = roc_curve(preds["trueLabel"],preds["anomalyScore"])
areaUnderROC = auc(fpr,tpr)
#AUC曲線
plt.figure()
plt.plot(fpr,tpr,color="r",lw=2,label="ROC curve")
plt.plot([0,1],[0,1],color="k",lw=2,linestyle="--")
plt.xlabel("False positive Rate")
plt.ylabel("True Postive Rate")
plt.ylim([0,1.05])
plt.xlim([0,1.0])
plt.title("Receiver operating characteristic: Area under the curve = {0:0.2f}".format(areaUnderROC))
plt.legend(loc="lower right")
plt.show()
if returnPreds == True:
return preds
この関数では、正解データのラベルと異常値を格納したdataframeを作成しています。
ポイントとなる関数はprecision_recall_curveとroc_curveです。
precision_recall_curveではしきい値を1から0に変化させたときの適合率と再現率を計算する関数です。
例えば、しきい値が0のとき、0以上をすべてエラーと判断します。つまり全てがエラーと判断されるわけです。こうなると、適合率は0に再現率は1になります。これを各しきい値ごとに計算してくれる便利な関数です。
roc_curveでは偽陽性率(False Positive Rate)と真陽性率(True Positive Rate)を各しきい値ごとに計算します。
例えば、しきい値が0のとき、0以上をすべて陽性と判断します。そうすると真陽性率は偽陰性が0件のため1となります。また、偽陽性率も真陰性が0件のため1となります。こんなふうに様々なしきい値での割合をけいしてくれる便利な関数です。
オートエンコーダによる異常検知の評価結果
それでは、実際にさきほど実装したオートエンコーダの評価結果です。
まずは適合率-再現率のグラフから。
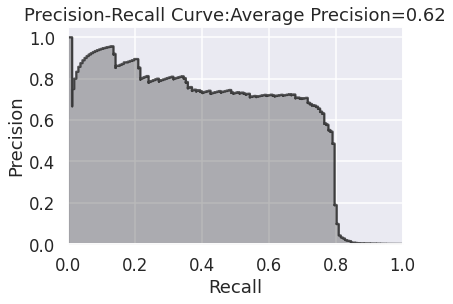
横軸の再現率が75%のとき、縦軸の適合率の値は60%ほどになっていますね。これはつまり、不正利用の75%を捉えることができて、そうやって捉えた不正利用の60%が実際に不正データである、ということを示しています。
次にauROC曲線です。
偽陽性率を低く抑えながら真陽性率を高くするための指標になります。このときの指標は0.92となりました。
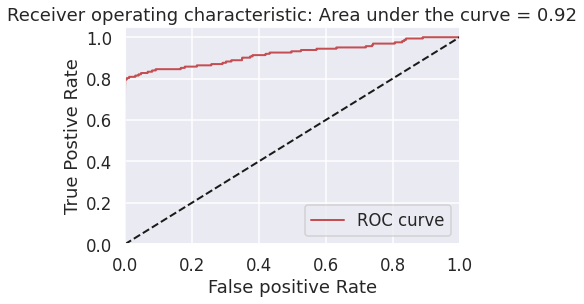
これらの結果より、正解データを用いた学習をさせなくともある程度の分類が可能であることがわかりました。更に精度を上げるためには、学習に
- dropoutを導入する
- 活性化関数を変化させる
- 圧縮させるときのノード数を変化させる
が考えられます。
終わりに
教師なし学習では、ラベルデータが大量になくとも学習が可能なこと、データの変化に対して柔軟なことが強みです。
個人的には、機械学習で勝手にデータの背後にある構造を理解しているのが面白く感じます。いったいどうやって学習しているんだろうか...。なかなか想像して言語化するのが難しい世界ですね。
本の中では、他にも識別するのみでなく、実際にデータを生成するための方法も紹介されています。(制限付きボルツマンマシン、深層学習、GANなど)
皆様の学習の参考になりましたら幸いです。