ノルム最小解
[最小二乗解についての記事]
(https://qiita.com/takseki/items/8114eb537a7fe78ca8f8 "最小二乗解") に引き続き、$ x $ についての(連立)線形方程式
$$ Ax=b $$ が解けない場合について考えます1。
最小二乗解について復習します。
$m>n$($A$ が縦長)のとき、条件の方が変数よりも多く、方程式としては不能(解なし)で、$ || Ax-b ||^2 $ が最小になるような $\hat{x}$ は
$$\hat{x}=(A^TA)^{-1}A^T b$$ と求められ、これを最小二乗解と呼ぶのでした。
$ Ax=b $ が一意に解けない場合として、もう1つあります。
それは、$m<n$($A$ が横長)のときで、この場合、条件よりも変数が多く、方程式としては不定で、$ Ax=b $ を満たす解は無数に存在します。
このような場合、無数の解のうち、$ ||x||^2 $ が最小になるような $\hat{x}$ を求めることが多々あります。これはノルム最小解と呼ばれ、
$$\hat{x}=A^T(AA^T)^{-1} b$$ と求められることが知られています。
最小二乗解のときと同様、この表式を射影の概念を利用して導出してみます。
射影による導出
$A$ が $2\times3$ 行列として、図を描いて考えてみます。
$x$ は3次元空間上のベクトル、$b$は2次元空間上のベクトルです。
$x$ は3次元空間上のベクトルですが、$A$を作用させた$Ax$ は2次元に押しつぶされます。
3次元空間のうち、$A$ によって押しつぶされる空間は$A$の核と呼び、$\mathrm{Ker}(A)$ と書きます。
この例だと、$\mathrm{Ker}(A)$ は 1次元です。
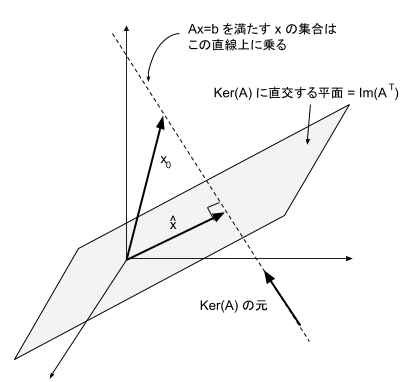
$Ax=b$ を満たすような $x_0$ を1つ取ってくると、これに $\mathrm{Ker}(A)$ の任意の元を加えたものも $Ax=b$ を満たします。したがって、$Ax=b$ を満たすような $x$ の集合は図のような直線で表せます。
このうち、$||x||$ が最小になる場合を考えると、これは明らかに、$x$ が $\mathrm{Ker}(A)$ の成分を持っていない場合です。
したがって、ノルム最小解は、$x_0$ を $\mathrm{Ker}(A)$ と直交する空間に正射影すれば得られることが分かります。
実は、この「$\mathrm{Ker}(A)$ と直交する空間」は $A^T$ の像 $\mathrm{Im}(A^T)$ と一致します。
理由は後で説明するとして、とりあえずこれを受け入れて先に進みます。
ここまでで分かったことは、「ノルム最小解は、適当な解 $x_0$ を $\mathrm{Im}(A^T)$ に正射影すれば得られる」ということです。後は、射影行列の知識を使えば簡単です。
$x$ を $\mathrm{Im}(A^T)$ へ正射影したベクトルは射影行列 $P$ を使えば、
$$x_{\mathrm{Im}(A^T)} = Px = A^T (A A^T)^{-1} A x$$ と書けます。
すると、$Ax_0=b$ を満たす適当な $x_0$ に対して、正射影をとったものがノルム最小解 $\hat{x}$ であるということは、
$$ \hat{x} = Px_0 = A^T (AA^T)^{-1} Ax_0 = A^T (AA^T)^{-1} b $$ と書けます。したがって、$$\hat{x}=A^T(AA^T)^{-1} b$$であることが分かりました。
補足
途中で説明を飛ばした、「$\mathrm{Ker}(A)$ と直交する空間は $\mathrm{Im}(A^T)$ と一致する」理由は以下のように示せます。
$x \in \mathrm{Ker}(A)$ について、$x' \in \mathrm{Im}(A^T)$ と内積をとると、
$$ (x', x) = (A^Ty, x) = (y, Ax) = (y, 0) = 0 $$ となる。よって、$\mathrm{Im}(A^T)$ は $\mathrm{Ker}(A)$ と直交する。
まとめ
最小二乗解とノルム最小解についてまとめると、$Ax=b$ について、
- $A$が縦長のとき、解は存在しないが、最小二乗解は $\hat{x}=(A^TA)^{-1}A^T b$
- $A$が横長のとき、解は無数に存在し、そのうちのノルム最小解は $\hat{x}=A^T(AA^T)^{-1} b$
なお、$b$ に掛かっている部分を1つの行列としてまとめたものは、(ムーア・ペンローズ型)一般逆行列とか、疑似逆行列、擬逆行列などと呼ばれるものに相当します。
機械学習の分野においては、最小二乗解は線形回帰問題で現れるのに対して、ノルム最小解はカーネル回帰で登場します。
これについてはまた別の記事で書けたらと思います。
-
今回も $A$ にランク落ちがないことを前提とします。つまり、$A$ が行フルランクか列フルランクのどちらかであるとします。 ↩