最小二乗解
$ x $ についての(連立)線型方程式
$$ Ax=b $$ を考えます。
$A$が $m \times n$ の実数行列で、$x$ が $n$ 次元のベクトル、$b$ が $m$ 次元のベクトルです。
$A$が正則であれば、$x=A^{-1}b$ と一意に解けますが、工学的な応用では、むしろこれが解けない場合を扱うことが多くあります。
$m>n$($A$ が縦長)であるすると1、条件の方が変数よりも多く、方程式としては不能(解なし)です。
最小二乗解の一番正統な(?)導出は、以下のように微分を使う方法です。
$ || Ax-b ||^2 $ を $x$ で微分して 0 とおくと、$ 2 A^T (A x - b) = 0 $ だから、最小二乗解 $\hat{x}$ が満たすべき方程式(正規方程式)は、
$$ A^T A \hat{x} = A^T b $$ と得られる。よって、最小二乗解は $\hat{x}=(A^TA)^{-1}A^T b$ と求められる2。
しかし、最小二乗解は部分空間への射影として得られるという側面があり、これを理解することが、部分空間法やカルマンフィルタなどの応用上重要になります。
そこで、この記事では、最小二乗解の射影による解釈について考えてみます。
射影行列による理解
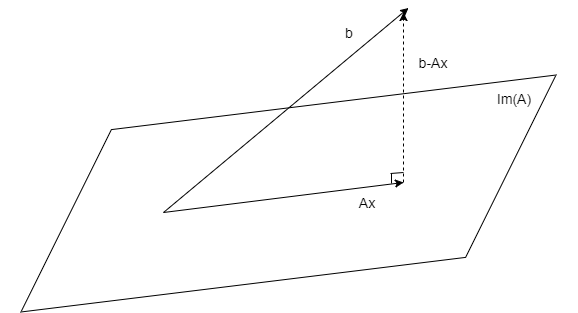
$A$ が $3\times2$ 行列として、図を描いて考えてみます。
$x$ を動かすと、$Ax$ は平面上の色々なベクトルを取ります。この平面は $A$の像 $\mathrm{Im}(A)$ です。
一方、$b$ は3次元空間上のベクトルであり、この平面外の成分を持つので、$Ax$ は $b$ と一致し得ません。
そこで、$||Ax-b||$ が最小になる場合を考えると、これは図のように、$Ax$ が $b$ を平面へ正射影したベクトルになっているときです。
$b$ を $\mathrm{Im}(A)$ へ正射影したベクトルは射影行列(前回記事) $P$ を使えば、
$$b_{\mathrm{Im}(A)} = Pb = A (A^T A)^{-1} A^T b$$ と書けます。
すると、$Ax$ が $b$ の正射影になっているという条件は、
$$A x = A (A^T A)^{-1} A^T b$$ と書けます。したがって、$$\hat{x}=(A^TA)^{-1}A^T b$$であることが分かります。
直交原理
$Ax$ が $b$ の正射影である、というのは、言い換えると、$A x - b$ が $A$ の像 $\mathrm{Im}(A)$ に直交することです。
これは、$A$ の列ベクトル $\{a_i\}$ を使えば、
$$a_i \cdot (Ax-b) = 0$$ であり、行列でまとめて書くと、
$$A^T (Ax-b) = 0$$ となり、やはり正規方程式が得られます。
$A \hat{x} - b$ が $A$ の像 $\mathrm{Im}(A)$ に直交するという性質は、「直交原理」とも呼ばれ、応用上重要になります。