【論文読解】NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections

概要

画像集合をもとに新しい視点からの画像を合成する技術であるNeRF in the Wild（NeRF-W）について紹介します。

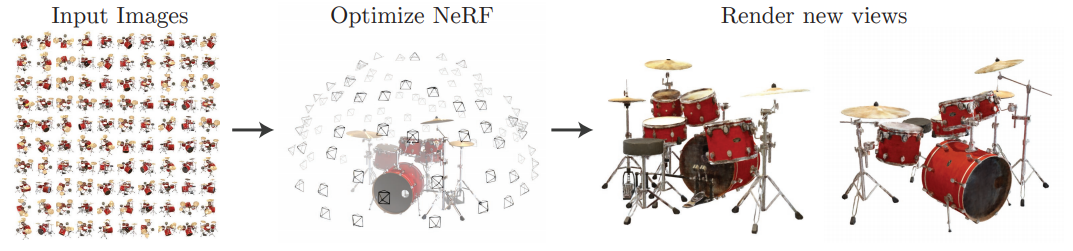
例えば、Photo Tourism Datasetには、ある特定のランドマークを様々な位置から撮影した写真が多数含まれています。そのような画像集合から、ランドマークの3次元的な形状を把握し、写真集合には含まれない新しい視点から見たときの合成画像を作成することができる、というのが目的となります。新しい視点からの合成結果をつなぎ合わせると、公式のプロジェクトページ内にあるような動画も生成することができます。

先行手法として、もともと提案されていたNeRF¹という手法がありましたが、本手法は天候の変化やオクルージョンが発生している自然な写真の集合でも効果的にモデルを構築できる工夫を盛り込んでいます。本手法はNeRFに大きく依存しているので、この記事では、まずはNeRFについて復習したのち、NeRF-Wでどのような工夫が行われたのかを確認していきます。

書誌情報

• Martin-Brualla, Ricardo, et al. "NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections." arXiv preprint arXiv:2008.02268 (2020).
• https://arxiv.org/abs/2008.02268
• 公式プロジェクトページ

NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

まずは先行手法であるNeRFの復習をしていきます。NeRFの目的は、様々な視点から撮影された画像集合からその集合に特化したモデルを構築し、新しい視点からの画像を合成できるようにすることです。

NeRFではボリュームレンダリングと呼ばれるレンダリング方法を採用するので、まずはそれについてみていきます。その後、NeRFで構築するモデルについて説明します。

ボリュームレンダリング

ボリュームレンダリングでは、3次元空間上にある点$\mathbf{x}=(x,y,z)$をある方向$\mathbf{d}=(d_x, d_y, d_z)$から見ると、色$\mathbf{c}=(r,g,b)$と密度$\sigma$が決まる、と考えます。

このような位置・方向から色・密度を決定できるとすると、ある位置$\mathbf{o}$にカメラがあるときに、そのカメラによって撮影される画像のピクセルの値は、$\mathbf{o}$からそのピクセルに対応する投影面上の点$\mathbf{r}$を通る光線$\mathbf{o} + t \mathbf{d}$（ここで、$t \in \mathbb{R}$）上に存在する色と密度によって下式のように決まります。

\begin{aligned} \overline{\mathbf{C}}(\mathbf{r}) &=\int_{t_{n}}^{t_{f}} T(t) \sigma(t) \mathbf{c}(t) d t \\ \text { where } \quad T(t) &=\exp \left(-\int_{t_{n}}^{t} \sigma(s) d s\right) \end{aligned}

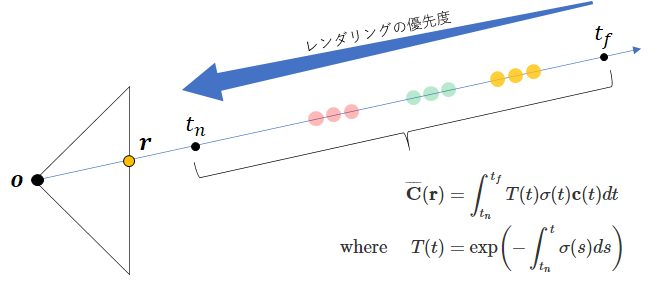
何をやっているのかを分かりやすくするために作図してみました。

光線上に、色$\mathbf{c}(t)$と密度が$\sigma(t)$が分布しています。投影面上の点$\mathbf{r}$における色は、この光線上にある色と密度を足し合わせることで計算されます。これは、$\int_{t_{n}}^{t_{f}}dt$によって表現されます。$t_n, t_f$はレンダリングの範囲であるビューボリュームを決める値で、極端にカメラから近い位置や遠い位置はレンダリングの対象外ということを表します。光線上にある色と密度を足し合わせるとはいえ、ただ単に足し合わせるわけにはいきません。というのも、カメラに近い位置に高密度な色が存在している場合は、その奥に何があるかに関わらず近い位置の色が優先されてレンダリングされるためです。これを制御するのが$T(t)$となっています。

実際には、積分操作はサンプルされたいくつかの$t_k (k=1,2,...,K)$によって以下のような近似が行われます。ここで、$\alpha(x)=1-\exp (-x)$、$\delta_{k}=t_{k+1}-t_{k}$です。このとき、$t_k$をどのようにサンプリングするかについては議論の余地がありますが、後述します。

\begin{aligned} \hat{\mathbf{C}}(\mathbf{r}) &=\sum_{k=1}^{K} \hat{T}\left(t_{k}\right) \alpha\left(\sigma\left(t_{k}\right) \delta_{k}\right) \mathbf{c}\left(t_{k}\right) \\  \text { where } & \hat{T}\left(t_{k}\right)=\exp \left(-\sum_{k^{\prime}=1}^{k-1} \sigma\left(t_{k}\right) \delta_{k}\right) \end{aligned}

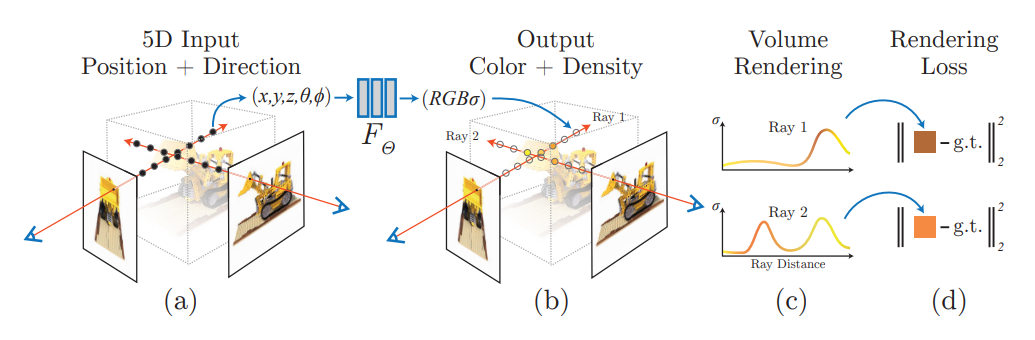
NeRFでは、$(\mathbf{x}, \mathbf{d})$から$(\mathbf{c},\sigma)$を求めることができるモデル$F_{\theta}(\mathbf{x}, \mathbf{d}) = (\mathbf{c},\sigma)$を構築します。これさえ構築できれば、仮想的なカメラの内部パラメータと外部パラメータを設定することで、各ピクセルに対応する光線上で上記の積分を行い、新しい視点からの画像をレンダリングできます。

NeRF

NeRFの目標は、与えられた画像集合から、モデル$F_{\theta}(\mathbf{x}, \mathbf{d}) = (\mathbf{c},\sigma)$を構築することです。

前提条件として、画像集合内の各画像の内部パラメータと外部パラメータは既知であるということが挙げられます。制御された環境のもと人工的に構築されたデータセットではこれは容易です。一方、現実的な写真集合に対してはひと手間必要で、NeRFおよびNeRF-Wでは事前にCOLMAP packege²を用いてStructure from Motionが適用し、各画像の内部パラメータと外部パラメータを求められています。

各画像の内部パラメータと外部パラメータ、およびモデル$F_{\theta}$が与えられていれば、ボリュームレンダリングによってレンダリング画像を得ることができます。レンダリング画像が実際の画像とどのように異なっているのかを比較し、それをもとに損失関数とすることで、モデル$F_{\theta}$を訓練することができます。

モデルの具体化と訓練

モデル$F_{\theta}(\mathbf{x}, \mathbf{d})$の具体的な形と訓練方法について、以下の3点を中心にみていきます。

• 点$\mathbf{x}=(x, y, z)$と方向$\mathbf{d}=(d_x, d_y, d_z)$を高次元の特徴量にエンコードするPositional Encoding$\gamma$
• 特徴量から密度$\sigma$と色$\mathbf{c}$を推定するモデル
• 粗いモデルと精細なモデルの組み合わせによる階層的なサンプリング

まず、Positional Encoding$\gamma$では、$(x, y, z, d_x, d_y, d_z)$といったそれぞれの実数が、$\mathbb{R}^{2L}$の空間にエンコードされます。それぞれの値は事前に$p \in [-1,1]$ の範囲に収まるように正規化されています。

\gamma(p)=\left(\sin \left(2^{0} \pi p\right), \cos \left(2^{0} \pi p\right), \cdots, \sin \left(2^{L-1} \pi p\right), \cos \left(2^{L-1} \pi p\right)\right)

NeRFにおいては、$x, y, z$では$L=10$、$d_x, d_y, d_z$ では$L=4$とされています。NeRF-Wにおいては、Positional Encodingはやや異なった手法が採用されていますが後述します。

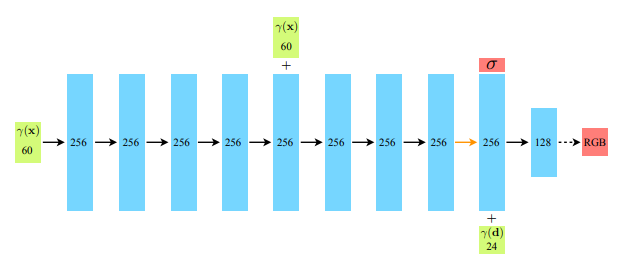
次に、密度$\sigma$と色$\mathbf{c}$を推定するモデルは以下のようなMLPによって実現されます。密度$\sigma$は$\mathbf{d}$とは無関係に出力されるということを確認しておきましょう。

最後の階層的なサンプリングについて説明します。ボリュームレンダリングでは、数値積分のために光線上の何点かをサンプリングする必要がありますが、その戦略を決める必要があります。 NeRFでは、粗いモデルでは均等にサンプリングし、細かいディテールを把握すべき領域の目星をつけ、精細なモデルではその領域を重点的にサンプリングするという階層的なサンプリングを行います。

粗いモデルでは、以下のように等間隔な$N_c$個のビンから$t_i$をサンプリングします。

t_{i} \sim \mathcal{U}\left[t_{n}+\frac{i-1}{N_c}\left(t_{f}-t_{n}\right), t_{n}+\frac{i}{N_c}\left(t_{f}-t_{n}\right)\right]

粗いモデルでサンプリングされた点の密度を用いることで、より重点的にサンプリングすべきビンがわかります。そのサンプリングの重みは、$w_{i}=\hat{T}(t_i)$を用いて、$\hat{w}_{i}= \frac{w_{i}}{\sum_{j=1}^{N_{c}} w_{j}}$と求めることができます。

損失関数

損失関数は、粗いモデルと精細なモデルの再構成誤差を足し合わせて、以下のように計算されます。$\mathcal{R}$は画像中の全ピクセルを表します。

\mathcal{L}=\sum_{\mathbf{r} \in \mathcal{R}}\left[\left\|\hat{C}_{c}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}+\left\|\hat{C}_{f}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}\right]

以上、駆け足でしたが、NeRFのおさらいでした。

NeRF-W

本題であるNeRF-Wの説明に移ります。NeRF-Wでは、NeRFの基本的な問題設定を受け継ぎつつ、大きく2つの問題に対処しています。

• 天候などの照明変化を明示的にモデルに組み込む
• 通行人や車などの一時的に映っている物体も明示的にモデルに組み込み、レンダリング結果を分布として推定する

また、細かいところでは、Positional Encodingの方法を変えていたりします。

以下、詳しく見ていきます。

Latent Appearance Modeling

NeRFは仕組み上、位置$\mathbf{x}$と方向$\mathbf{d}$に対して一意に密度$\sigma$や色$\mathbf{c}$が定まります。密度はともかく、時間帯や天候によって見える色は変化するので、このような前提は現実の写真をもとに構築するモデルとしては不適切と言えます。

そこで、画像ごとに定まるappearance embedding$\mathbf{\ell}_i^{(a)}$を想定し、これによって色が変化するというモデルを考えます。

以降の説明のために、MLPを2つの部分に分割してみます。1つ目のMLPでは位置$\mathbf{r}(t)$のPositional Encoding$\gamma_{\mathbf{x}}(\mathbf{r}(t))$を用いて密度$\sigma$と中間表現$\mathbf{z}$を推定し、2つ目のMLPではそれに方向$\mathbf{d}$のPositional Encoding$\gamma_{\mathbf{d}}(\mathbf{d})$と中間表現$\mathbf{z}$を用いて、色$\mathbf{c}$を推定する、という形になっています。

\begin{aligned}
(\sigma(t), \mathbf{z}(t)) &=\operatorname{MLP}_{\theta_{1}}\left(\gamma_{\mathbf{x}}(\mathbf{r}(t))\right) \\ \mathbf{c}(t) &=\operatorname{MLP}_{\theta_{2}}\left(\mathbf{z}(t), \gamma_{\mathbf{d}}(\mathbf{d})\right) \end{aligned}

$\mathbf{\ell}_i^{(a)}$は色を調整する特徴量になるので、導入するとしたら2つ目のMLPになり、以下のような形に修正されます。

\mathbf{c}_{i}(t)=\operatorname{MLP}_{\theta_{2}}\left(\mathbf{z}(t), \gamma_{\mathbf{d}}(\mathbf{d}), \ell_{i}^{(a)}\right)

各画像ごとの特徴量である$\mathbf{\ell}_i^{(a)}$は、Generative Latent Optimization³の枠組みで最適化されます。この最適化は、GLOの論文の表記では各画像の特徴量は$z_i$、生成モデルは$g_{\theta}$、損失関数は$\ell$を用いて、以下のような入れ子の最小化問題として表現されます。

\min_{\theta \in \Theta} \frac{1}{N} \sum_{i=1}^N \left[ \min_{z_i \in Z} \ell(g_{\theta}(z_i), x_i) \right]

現実的には、特徴量$z_i$と生成モデル$g_{\theta}$は交互に更新されるというGANのような手順で最適化されます。なお、$z$の更新の際は、$\max \left(|z|_{2}, 1\right)$で割って、できるだけ単位超球面上に存在するように正規化されます。

というわけで、画像ごとに用意された特徴量$\mathbf{\ell}_i^{(a)}$は、GLOの枠組みでランダムに初期化されたのち、MLPと交互に更新されます。

Transient Objects

次に、写真にたまたま写りこんでいる一時的な物体を明示的にモデルに組み込みます。一時的な物体にも密度と色があると想定し、それを$\sigma_i^{(\tau)}, \mathbf{c}_i^{(\tau)}$と表記します。一時的な物体は個々の画像に固有なので、画像インデックスを表す下付き添え字$i$が付いています。

このような、各画像に固有の新たな密度と色を盛り込むと、レンダリングを表す数式は以下のように修正されます。

\begin{array}{l} \overline{\mathbf{C}}_{i}(\mathbf{r})= \int_{t_{n}}^{t_{f}} T_{i}(t)\left(\sigma(t) \mathbf{c}_{i}(t)+\sigma_{i}^{(\tau)}(t) \mathbf{c}_{i}^{(\tau)}(t)\right) d t \\ \text { where } T_{i}(t)=\exp \left(-\int_{t_{n}}^{t}\left(\sigma(s)+\sigma_{i}^{(\tau)}(s)\right) d s\right) \end{array}

ここで、さらに色の不確実性というアイディアを導入します。写真にたまたま写りこんでいる「一時的な物体」の中には、撮影しているカメラそのものによって生じる誤差や撮影対象の特定の部位の反射強度の揺らぎといった誤差も含まれます。そのような不確実性を表すような$\beta_i$を導入します。$\beta_i(\mathbf{r}(t))$は3次元上の点ごとに定められ、レンダリング画像の特定ピクセルについての不確実性$\beta_i(\mathbf{r})$は、ピクセルに対応する光線上の積分で求められます。

\begin{array}{l}
\beta_{i}(\mathbf{r})=\int_{t_{n}}^{t_{f}} T_{i}^{(\tau)}(t) \sigma_{i}^{(\tau)}(t) \beta_{i}(t) d t \\
\text { where } T_{i}^{(\tau)}(t)=\exp \left(-\int_{t_{n}}^{t} \sigma_{i}^{(\tau)}(s) d s\right)
\end{array}

このような不確実性を導入すると、最終的なピクセル値$\mathbf{C}_i(\mathbf{r})$は、以下のようなガウス分布として推定されます。

\mathbf{C}_{i}(\mathbf{r}) \sim \mathcal{N}\left(\overline{\mathbf{C}}_{i}(\mathbf{r}), \beta_{i}(\mathbf{r})^{2} \mathbb{I}_{3}\right)

以上のような一時的な物体と不確実性である$\sigma_i^{(\tau)}, \mathbf{c}_i^{(\tau)}, \beta_i$を求めるモデルを考えます。Appearanceと同様に、画像ごとに用意されている特徴量であるtransient embedding$\mathbf{\ell}_i^{(\tau)}$を想定します。この特徴量と1つ目のMLPによって得られる中間表現$\mathbf{z}$から、密度$\sigma_i^{(\tau)}$と色$\mathbf{c}_i^{(\tau)}$、そして色の不確実性$\beta_i$を推定する以下のような3つ目のMLPが考えられます。ここで、$\beta_{\text{min}}$は色の分散が0にならないようにするための補正値です。

\begin{array}{c} {\left[\sigma_{i}^{(\tau)}(t), \mathbf{c}_{i}^{(\tau)}(t), \tilde{\beta}_{i}(t)\right]=\operatorname{MLP}_{\theta_{3}}\left(\mathbf{z}(t), \ell_{i}^{(\tau)}\right)} \\ \beta_{i}(t)=\beta_{\min }+\log \left(1+\exp \left(\tilde{\beta}_{i}(t)\right)\right) \end{array} 

ピクセルの色を点ではなく分布で推定することになるので、NeRFと同様の2乗誤差による損失関数をそのまま適用するわけにはいきません。そこで、ガウス分布に対する負の対数尤度のような、以下のような損失関数が用いられます。

L_{i}(\mathbf{r}) = \frac{1}{2 \beta_{i}(\mathbf{r})^{2}}\left\|\mathbf{C}_{i}(\mathbf{r})-\hat{\mathbf{C}}_{i}(\mathbf{r})\right\|_{2}^{2} +\frac{1}{2} \log \beta_{i}(\mathbf{r})^{2}+\frac{\lambda_{u}}{K} \sum_{k=1}^{K} \sigma_{i}^{(\tau)}\left(t_{k}\right)

右辺第1項はほぼ2乗誤差ですが、$\beta_i$が大きいときには損失の大きさを軽減するという項になっており、不確実性が高い場合は2乗誤差を考慮しなくてよいというものになります。一方で、右辺第2項はどこもかしこも不確実ということにならないように、$\beta_i$の大きさに制限を与える正則化項です。最後に、右辺第3項は一時的な物体の密度$\sigma_i^{(\tau)}$ができるだけスパースになるように、という別の正則化項です。一時的な物体は、定義上局所的にしか存在していないので、このような正則化が適しています。

NeRFでは粗いモデルと精細なモデルという2つのモデルを同時に訓練していましたが、それはNeRF-Wでも同様です。ここまで示した複雑なモデルは精細なモデルでのみ採用し、粗いモデルではNeRFと同様のものを採用します。

全体の損失関数は以下のようになります。

\sum_{i j} L_{i}\left(\mathbf{r}_{i j}\right)+\frac{1}{2}\left\|\mathbf{C}\left(\mathbf{r}_{i j}\right)-\hat{\mathbf{C}}_{c}\left(\mathbf{r}_{i j}\right)\right\|_{2}^{2}

NeRF-Wのまとめと補足

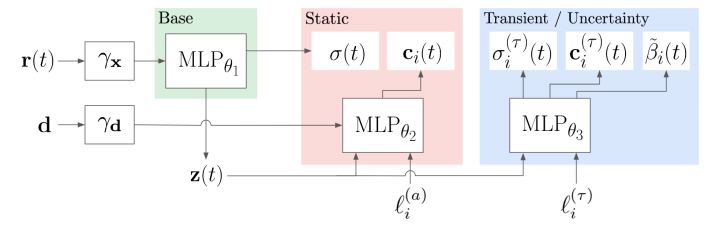
まとめると、NeRF-Wにおけるモデルは以下のような構造になっています。

2つ目のMLPの出力を用いてStaticな結果を、3つ目のMLPの出力も組み合わせて一時的な物体も含めた結果を得ることができます。各段階の出力をレンダリングしたときの結果を表したのが、以下の画像の(a)(b)(c)です。

Static(a)は、リファレンスとして与えられている一番右の画像(e)のカメラパラメータと訓練の過程で最適化された$\mathbf{\ell}_i^{(a)}$を用いてレンダリングされます。一方、訓練の過程で最適化された$\mathbf{\ell}_i^{(\tau)}$を用いることで、画像に固有の一時的な物体の画像(b)をレンダリングすることができます。双方を組み合わせることでレンダリング結果(c)を得ることができます。

(d)は不確実性のマップです。通行人のような移動物体の領域で大きくなっていることが確認できる一方で、複雑な構造を持つ物体の境界領域でも大きくなっていることが確認できます。

なお、新規視点の画像得るための推論時には、Staticな画像さえ得られればいいので、一時的な物体や不確実性に関する推論は不要になります。一方で、$\mathbf{\ell}_i^{(a)}$は色合いをコントロールする特徴量であり、この値を調整することで、以下のように多様な照明条件のレンダリング結果を得ることができます。

最後に、Positional Encodingについて補足しておきます。NeRF-WではNeRFとは異なるPositional EncodingであるFourier features⁴を採用しています。Fourier featuresの元論文ではいくつかの方法を提案しているのですが、最も性能が良いとされているGaussianバージョンを以下に示します。$\sin, \cos$を用いていることは従来のものと一緒ですが、各要素が正規分布$\mathcal{N}\left(0, \sigma^{2}\right)$からサンプルされるランダムな行列である$\mathbf{B} \in \mathbb{R}^{m \times d}$が使われていることが異なります。$\sigma^{2}$はハイパーパラメータです。

\gamma(\mathbf{v})=[\cos (2 \pi \mathbf{B} \mathbf{v}), \sin (2 \pi \mathbf{B} \mathbf{v})]^{\mathrm{T}}

この手法では、Positional Encodingによって$d$次元の位置や方向は、$2m$次元の特徴量に変換されます。

まとめ

以上、NeRFおよびNeRF-Wについて紹介しました。3月ごろにNeRFが発表されたときは、面白そうだなと思いつつも積んでいました。半年もたたないうちにNeRF-Wのような改善手法が発表され、そういえばと思い出し、併せて読んでみたという感じです。

細かいハイパーパラメータや実装はまだ公開されていないので、公開を楽しみに待ちたいと思います。

1. Ben Mildenhall, Pratul P. Srinivasan, Matthew Tancik, Jonathan T. Barron, Ravi Ramamoorthi, and Ren Ng. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. ECCV, 2020. ↩

2. https://demuc.de/colmap/ ↩

3. Piotr Bojanowski, Armand Joulin, David Lopez-Pas, and Arthur Szlam. Optimizing the latent space of generative networks. ICML, 2018 ↩

4. Matthew Tancik, Pratul P. Srinivasan, Ben Mildenhall, Sara Fridovich-Keil, Nithin Raghavan, Utkarsh Singhal, Ravi Ramamoorthi, Jonathan T. Barron, and Ren Ng. Fourier features let networks learn high frequency functions in low dimensional domains, 2020. ↩