概要
最近単眼深度推定の深層学習モデルについていくつか読んだので、何回かに分けて紹介していきます。
今回紹介するのは通称SfMLearnerと呼ばれる手法で、単眼(カメラが1つ)で深度を推定する手法、それも単眼で撮影された動画を元に、教師なしで学習できるという手法です。
「教師なし」と書いてますが、最近の用語でいうと自己教師あり(self supervised)と捉えたほうが実態には合っていると思います。
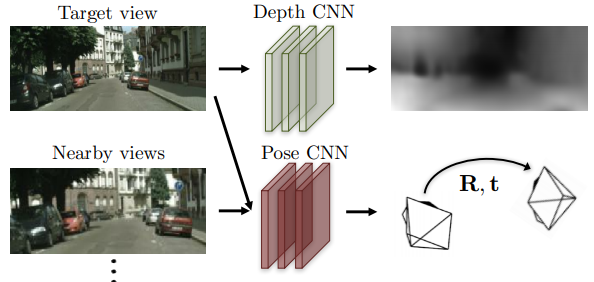
下図の左側が入力画像、右側が出力画像です。概ね、手前にある領域が白く、奥にある領域が黒くなっているということがわかります。
以下の順に説明してきます。
- 基本的なアイディア
- ネットワーク構造
- 損失関数
- Explainability Maskの確認
書誌情報
- Zhou, Tinghui, et al. "Unsupervised learning of depth and ego-motion from video." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017.
- プロジェクトページ
基本アイディア:なぜ単眼動画で深度が推定可能なのか
一般的によく知られている画像を元にした深度推定の手法は、ステレオカメラなど複数台のカメラを利用した手法です。例えば、ステレオカメラから得られた画像を比較して様々な物体領域について視差を算出し、それを元に深度を推定する、というものです。
本手法は、このような考え方とは異なっており、いわばセグメンテーションの連続値版のようなことをしています。つまり、1枚の入力画像を元に、深度マップ画像を出力するという考え方です。実際、本手法では、セグメンテーションでよく使われるアーキテクチャであるU-Net構造が採用されています。しかし、今回の設定では、ターゲットとなる深度マップの正解データが存在していないため、一般的な教師ありのセグメンテーション手法とは訓練プロセスの勝手が違います。
本手法では、深度マップの推定を間接的に最適化するための仕組みを作っています。
概ね、以下のような流れになっています。
- ターゲット画像$I_t$から深度マップ$\hat{D_t}$を推定する。
- ソース画像とターゲット画像$I_s, I_t$から、画像間のカメラの姿勢$\hat{T}_{t \rightarrow s}$、つまり視点の違いを推定する。
- 深度マップ$\hat{D_t}$とカメラの姿勢$\hat{T}_{t \rightarrow s}$を元に、$I_t$のピクセルと$I_s$の対応関係を求める。
- 3.で求めたピクセルの対応関係を元に、$I_s$から合成画像$\hat{I}_{s}$を生成する。この合成画像は、ターゲット画像に似ていることが期待される。
- 合成された画像$\hat{I}_{s}$と画像$I_t$とを比較し、損失を計算する。
手順3では、エピポーラ幾何の方法が使われます。ターゲット画像$I_t$上のピクセルが、ソース画像$I_s$上のピクセルとどのような対応をしているのかを求めています。この対応関係は、下式のような座標の変換として表されます。
$p_{s} \sim K \hat{T}{t \rightarrow s} \hat{D}{t}\left(p_{t}\right) K^{-1} p_{t}$
$K$はカメラの内部パラメータですが、入力画像$I_s, I_t$は共に同じカメラで撮影された動画の別フレームの画像であることから、同一のパラメータが使用されています。
この式は、右から順に3つの部分に分けて考えるとわかりやすいかと思います。
- $\hat{D}{t}\left(p{t}\right) K^{-1} p_{t}$:ターゲット画像$I_t$上のピクセル座標が、ターゲットカメラの座標系でどの座標になるのかを求める。
- $\hat{T}_{t \rightarrow s}$:ターゲットカメラの座標系からソースカメラの座標系に変換する。
- $K$:ソースカメラの座標系にある点を撮影し、ソース画像$I_s$上のピクセル座標に変換する。
なお、手順4は一見めんどくさい処理のように見えますが、PyTorchではgrid_sampleによって簡単に実装できます。他の深層学習フレームワークでも、大抵のものは実装されているでしょう。
以上のように、深度マップは、別途推定されるカメラ姿勢と併せて、合成画像とターゲット画像の差異を元にした損失を通じて間接的に訓練される、というわけです。
エピポーラ幾何についてはQiita内にもわかりやすい解説記事があるので確認してみてください。
ネットワーク構造
本手法は大きく分けて2つのことを推定する必要があります。一つはターゲット画像に対する深度マップ$\hat{D}{t}$で、もう一つはターゲットカメラに対するソースカメラの姿勢$\hat{T}{t \rightarrow s}$です。
これらは、それぞれ個別のネットワークによって推定されます。
下図におけるDepth CNNから出力されているのが深度マップで、Pose CNNから出力されているのがカメラの姿勢変化です。
以下、それぞれのネットワークについて見ていきます。
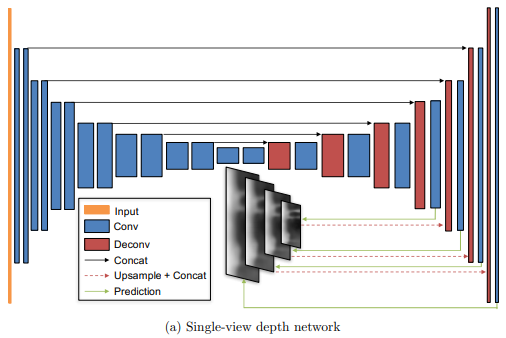
Depth CNN
Depth CNNは、深度マップを出力するネットワークです。
前述したとおり、U-Net構造を持っており、Encoder側で得られた特徴マップがDecoder側でも再利用されます。また、深度推定の出力は、入力画像と同じ解像度以外にも低解像度のものが何枚か出力されます(上図の中央下部)。また、低解像度の出力結果はより高解像度の出力を得るために再利用されます。このような構造によって、深度マップが低解像度から高解像度へと徐々に洗練されていくという効果が得られます。
深度は、合理的なスケールになるように以下のような変換が行われます。
$D = 1 /(\alpha * \operatorname{sigmoid}(x)+\beta)$
ここでは、$\alpha=10, \beta=0.1$が採用されます。
また、実験における評価では、さらに下式のようなスケール係数を掛けてあげて評価しているようです。
$\hat{s}= {median}\left(D_{g t}\right) / {median} \left(D_{p r e d}\right)$
いずれにせよ、本手法における深度マップのスケールはかなり曖昧性を残しているという点には注意が必要です。
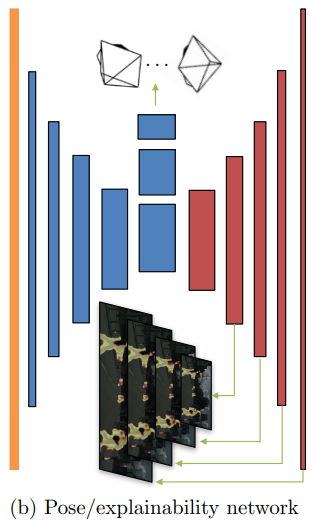
Pose CNN
Pose CNNは、$N$枚のフレーム画像から、1枚のターゲット画像に対する$N-1$枚のソース画像のカメラ姿勢を推定します。カメラの姿勢は6DoF(3つの回転、3つの平行移動)で表現される6次元の値なので、全体としては、$6(N-1)$次元の出力となります。
Explainability Mask
Pose CNNでは、カメラ姿勢の推定以外にも、Explainability Maskの推定も行います。
動画内には当然、車や人物のような動く物体が存在しています。
このような物体の領域は、合成画像$\hat{I}_{s}$とターゲット画像$I_t$とを比較して損失を計算する際に少々厄介です。というのも、複数のフレーム画像の間では、周囲の物体が動くということが想定されていないためです。そこで、このような領域は、原理的に合成が難しい領域ですので、損失の対象としないためにマスクする、という措置がとられています。
ところで、なぜカメラ姿勢の推定とマスクの推定を同じネットワーク内で行うのでしょうか? これについては、以下のような直感的な説明ができます。
背景のような静止している領域の変動からはカメラの姿勢変化を推定するのに役立つ情報が得られそうです。一方で、そのような変動とは全く異なる変動をしている領域は、例えば動いている物体なので、Explainability Maskとして推定する、という感じです。そのため、2つの推定対象は関連が深いため、同一ネットワークで行ったほうが良い、ということが言えそうです。
このExplainability Maskも、深度マップと同様に複数解像度で出力します。
なお、マスクは、$2(N-1)$チャネルになります。それぞれ$(N-1)$組のsource-targetの組に対応しており、2チャネルは0/1に対応しています。各組でsoftmaxが適応された後、その片割れのチャネルが$\hat{E_s}$すなわちExplainality Maskとして使用されます。
損失関数
本手法では、3種類の損失関数を用います。
合成画像の損失
ターゲット画像$I_t$と、ソース画像を元に合成された画像$\hat{I_s}$の比較を行い、損失とします。基本的には、すべてのsource-targetの組($s$)に対して、全ピクセル($p$)の絶対誤差をとって算出します。
$\mathcal{L}{v s}=\sum{s} \sum_{p}\left|I_{t}(p)-\hat{I}_{s}(p)\right|$
この計算式は最も素朴なもので、Explainability Maskはまだ適用されていません。マスク$\hat{E}_{s}$を適用すると、以下のようになります。ピクセルごとに損失をどのくらい真に受けるかが、これによって決まります。
$\mathcal{L}{v s}=\sum{s} \sum_{p} \hat{E}{s}(p)\left|I{t}(p)-\hat{I}_{s}(p)\right|$
深度マップの平滑化損失
一般に、深度マップは、あまりガタガタ変化するものではありません。
あるピクセルの深度は、隣のピクセルの深度とも概ね同じ、もしくはなだらかに変化するものです。そういうわけで、深度マップができるだけなめらかになるようなペナルティをかけるため、深度マップの02次勾配を計算し、それを損失としています。
PyTorchによる非公式実装では、以下のように実装されています。
def smooth_loss(pred_map):
def gradient(pred):
D_dy = pred[:, :, 1:] - pred[:, :, :-1]
D_dx = pred[:, :, :, 1:] - pred[:, :, :, :-1]
return D_dx, D_dy
if type(pred_map) not in [tuple, list]:
pred_map = [pred_map]
loss = 0
weight = 1.
for scaled_map in pred_map:
dx, dy = gradient(scaled_map)
dx2, dxdy = gradient(dx)
dydx, dy2 = gradient(dy)
loss += (dx2.abs().mean() + dxdy.abs().mean() + dydx.abs().mean() + dy2.abs().mean())*weight
weight /= 2.3 # don't ask me why it works better
return loss
Explainability Maskの正則化
Explainability Maskは、原理的に合成が困難な領域をマスクしてくれるという点では重要ですが、何でもかんでもマスクしてしまうと、合成画像の損失が0になってしまい、問題があります。そこで、できるだけ全体が1に近づくような正則化損失$\mathcal{L}_{reg}$を導入します。
Explainability Maskは、0/1を表す2チャネルの出力ですので、それができるだけ1に寄るように、クロスエントロピー誤差が適用されます。
全体
以上をまとめると、以下のような損失が定義できます。
$\mathcal{L}{\text {final}}=\sum{l} \left(\mathcal{L}{v s}^{l}+\lambda{s} \mathcal{L}{smooth}^{l}+\lambda{e} \sum_{s} \mathcal{L}{reg}\left(\hat{E}{s}^{l}\right) \right)$
ここで、$l$は複数の解像度、$s$は複数の$I_s, I_t$の組み合わせに対応しています。
Explainability Maskの確認
実験では、深度や姿勢の教師あり手法に迫る精度を実現できているということが示されていますが、細かい実験結果を示すことはここでは行わず、Explainability Maskがどのような役割を果たしているのかを確認します。
以下はExplainability Maskの出力例です。
歩行者や自転車といった物体領域(上から1-3行目)や、ターゲット画像には写っているけれどソース画像には写っていない物体(上から4-5行目)をマスクし、合成画像の評価時に原理的に困難な領域は無視するように訓練できていることがわかります。
一方で、残り2行の例では、ポールやその影といった細かい領域についても何故かマスクがかかっています。このような細い領域では深度推定がうまくできないために、マスクでごまかしてしまっている、という苦手なケースも確認できます。
まとめ
ざっとですが、論文で提案されている手法の解説を試みました。
この手法は、教師なし単眼深度推定手法の源流にあるだけあって、最新の手法の論文から振り返って見れば、まだまだ粗も多いことがわかります。特に、Explainability Maskは、論文中のディスカッションでも述べられている通り、原理的にソース画像からの合成が困難な場合に有用である一方で、オクルージョンが存在するという物体の前後関係を示す重要な幾何的情報を無視してしまうという欠点も持っています。
来週以降、後継手法について解説記事を書いていく予定です。