22日目を担当します、よろしくお願いします
スマホで見る方のために?ページ内リンク付き目次です
(インラインで数式いれるとスマホで見たとき変なところで改行される?からか, 見づらいかもしれません)
この記事の概要
NeurIPS 2019 pre-proceedings から選んだGNN(Graph Neural Networks)に関する説明法の論文(from Stanford Uni), GNNExplainer: Generating Explanations for Graph Neural Networks に関して紹介します.
論文に入る前に
さらっと説明できるAI(XAI)について書いておきます.
-
16日目の方の投稿にもありましたように, GoogleからeXplanable AI(XAI)についての発表が11月にありました.1
-
XAIはアメリカ国防高等研究計画局(DARPA)もプロジェクトの1つとして研究を進めています2
-
XAIに関する論文数は2015年から右肩上がりです3
-
AIの説明法は様々な物が提案されています.
- 解釈性の高いモデル, 説明法の分類はいくらかあります7
- intrinsic or post-hoc
- 決定木等の元から解釈性が高いアルゴリズムか, 学習済みのモデルに対する解析を行うアルゴリズムか
- model-specific or model-agnostic
- あるモデルのみに対するアルゴリズムか, 機械学習におけるモデルすべてに適応できるアルゴリズムか
- local or global
- localのみを考慮するアルゴリズムか(LIMEのように,説明したいデータ近傍で解釈性の高いモデルを作成し説明するなど), モデルの全体的な説明をするアルゴリズムか
- semantic or syntactic
- LIME,SHAP等のモデルが何を重視しているかの"意味"を出すアルゴリズムか,Featのような"構造的"にモデルを表すアルゴリズムか(これはまだ少ない?)
- intrinsic or post-hoc
今回紹介する論文では, AbstractでGNNExplainerはmodel-agnosticなアプローチと書いてありますが, おそらくGNNのモデルならすべて適応できるという意味で用いているのだと思います. つまり, GCNでもほかのモデルでも, GNNのモデルならすべて適応できるという意味でmodel-agnosticな手法ということです.
Intro
では,本題に入っていきます.GNNのサーベイ論文等を読むとIntroによく書いてある??ように,グラフは様々な実世界の問題を表現でき,GNNによって近傍データの特徴を良く加味した学習が可能になりました.
しかしGNNもその他高精度の手法と同様に?,透明性・解釈性が非常に高いわけではありません.そこで本論文はGNNに対する説明法,GNNExplainerを提案しています.
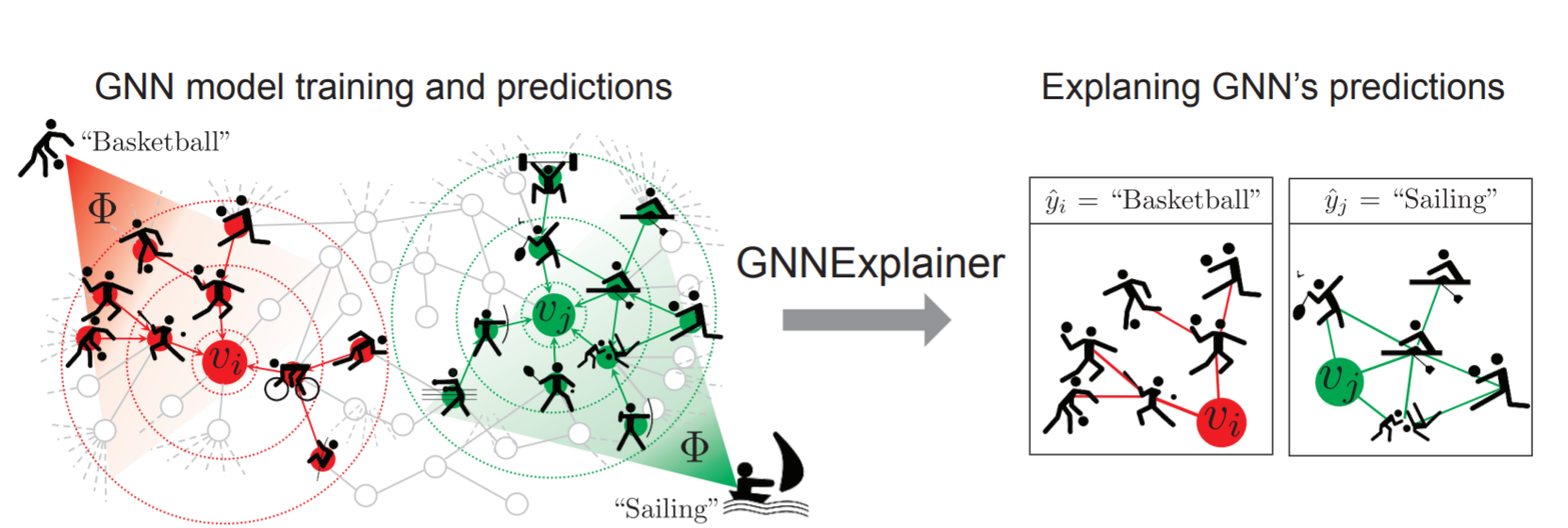
GNNExplainerの概要図は上の通りです.上のグラフは,ノードの1つ1つを1人の人間に対応するとします.タスクとしてはNode Classificationで,そのノードの人の好きなスポーツを予測するとすると,左図の赤いノード$v_i$をモデル$Φ$はバスケットボールと予測しています. その理由として, GNNExplainerはsubgraphを右図のように構築し, 周りにボールを使うスポーツが好きなノードが多いことからバスケットという予測を下したという説明ができます.
上の図からわかるように, GNNExplainerの入力は学習済みのGNNのモデルと説明したいインスタンスで, 出力は説明とするサブグラフを返します(サブ特徴量も返します,これについては次の章で).
Node Classificationなら, 近傍k-nodesをテキトーに持ってきてもそれっぽい説明になりそうだと思いましたが, GNNExplainerは, Graph Classification,Link Prediction等の別タスクに対しても適応可能で, 繰り返しですがGNNのモデルならすべて適応可能なアルゴリズムであることが, 論文中で主張されています.
GNNExplainer
では, GNNExplainerはどのようにSubgraphを決定するのか見ていきます.
GNNExplainerは以下の仮定の下で,サブグラフの隣接行列$A_{s}$の獲得を目指します($A_{c}$は元のグラフの隣接行列).
A_{S}[j, k] \leq A_{c}[j, k]
GNNExplainerのゴールは, あるノード$v$と学習済みのGNNモデルが与えられたときに, $v$に対するモデルの予測根拠をよく説明するようなサブグラフ$G_{S} \subseteq G_{c}$を獲得することです($G_{c}$は元のグラフ).
では,どのような$G_{S}$を獲得することを目指すかというと, 以下を最適化する$G_{S}$を最も良いグラフとします. ここで,$MI$は相互情報量, $X_{S}$をサブグラフの特徴量, $Y$を訓練後のGNNの予測ラベル分布とします.
\max _{G_{S}} M I\left(Y,\left(G_{S}, X_{S}\right)\right)=H(Y)-H\left(Y | G=G_{S}, X=X_{S}\right) \tag{1}
ここで, $H(Y)$は定数であるため(当たり前ですが,GNNモデル訓練後にGNNExplainerを使うため,$H(Y)$は固定), (1)を以下のように変換できます.
\min_{G_{S}} H\left(Y | G=G_{S}, X=X_{S}\right) \tag{2}
H\left(Y | G=G_{S}, X=X_{S}\right)=-\mathbb{E}_{Y | G_{S}, X_{S}}\left[\log P_{\Phi}\left(Y | G=G_{S}, X=X_{S}\right)\right]
(1)の最大化問題は, (2)のような条件付きエントロピーの最小化問題と言えます. (2)の下の式は, 期待値を使って条件付きエントロピーを表しています.
ハイパーパラメタとして,$K_{M}$を決め,$\left|G_{S}\right| \leq K_{M}$となるように元のグラフ$G_{C}$からエッジを取り除いていくのがGNNExplainerのアルゴリズムです. 学習済みモデル$Φ$の予測の曖昧さを最小にするように, 取り除くエッジを決め, サブグラフを決定します.
サブグラフの選択肢としては, 元のグラフが大きいほど指数関数的に多くあり, 直接最適化することは困難なため, サブグラフを$\mathcal{G}$から生じる確率変数と考えます($G_{S} \sim \mathcal{G}$).
\min _{\mathcal{G}} \mathbb{E}_{G_{S} \sim \mathcal{G}} H\left(Y | G=G_{S}, X=X_{S}\right) \tag{3}
凸性の仮定の下で, イェンセンの不等式から(3)の上界が以下のようになります. 凸性の仮定はGNN,DNNの複雑さから保たれないことが考えられますが, 実験的に正則化項とともに最適化して得たサブグラフが良い結果を得られていることを主張しています(論文中のp5, in practice~辺り).
\min _{\mathcal{G}} H\left(Y | G=\mathbb{E}_{\mathcal{G}}\left[G_{S}\right], X=X_{S}\right) \tag{4}
次のトリックですが, (4)の$\mathbb{E}_{\mathcal{G}}$を推定するために, 以下のように平均場近似を用います.
P_{\mathcal{G}}\left(G_{S}\right)=\prod_{(j, k) \in G_{c}} A_{S}[j, k]
これにより, サブグラフの隣接行列$A_{s}$の$(j, k)$要素, すなわち$\left(v_{j}, v_{k}\right)$にエッジが存在するかどうかをあらわす値をそれぞれ推定できます. よって(4)の期待値部分をサブグラフの隣接行列$A_{s}$に置き換えることができました.
サブグラフの隣接行列$A_{s}$は以下の式のように, 元グラフの隣接行列$A_{c}$にマスクをかけて獲得します.
$$A_{c} \odot \sigma(M)$$
これによって得られたサブグラフの隣接行列$A_{s}$にたいして, 適当なしきい値(0.5とか)を基準に最終的な隣接行列を決定します(隣接行列なので, 0か1にする). だらだら書いてきましたが, 最終的には以下のように, 最適なマスクMの獲得をGNNExplainerは目指します(中身はクロスエントロピーloss).
\min _{M}(-\sum_{c=1}^{C} \mathbb{1}[y=c] \log P_{\Phi}\left(Y=y | G=A_{c} \odot \sigma(M), X=X_{S}\right)) \tag{5}
(5)から得られたマスク$M$を元に, サブグラフ$G_{s}$を決定し, GNNExplainerの出力とします.
以上がサブグラフ決定のアルゴリズムです. ここからはサブ特徴量をどう獲得するか書いていきますが, 是非読み飛ばしてください(なんか長くなってきたから(^ω^))
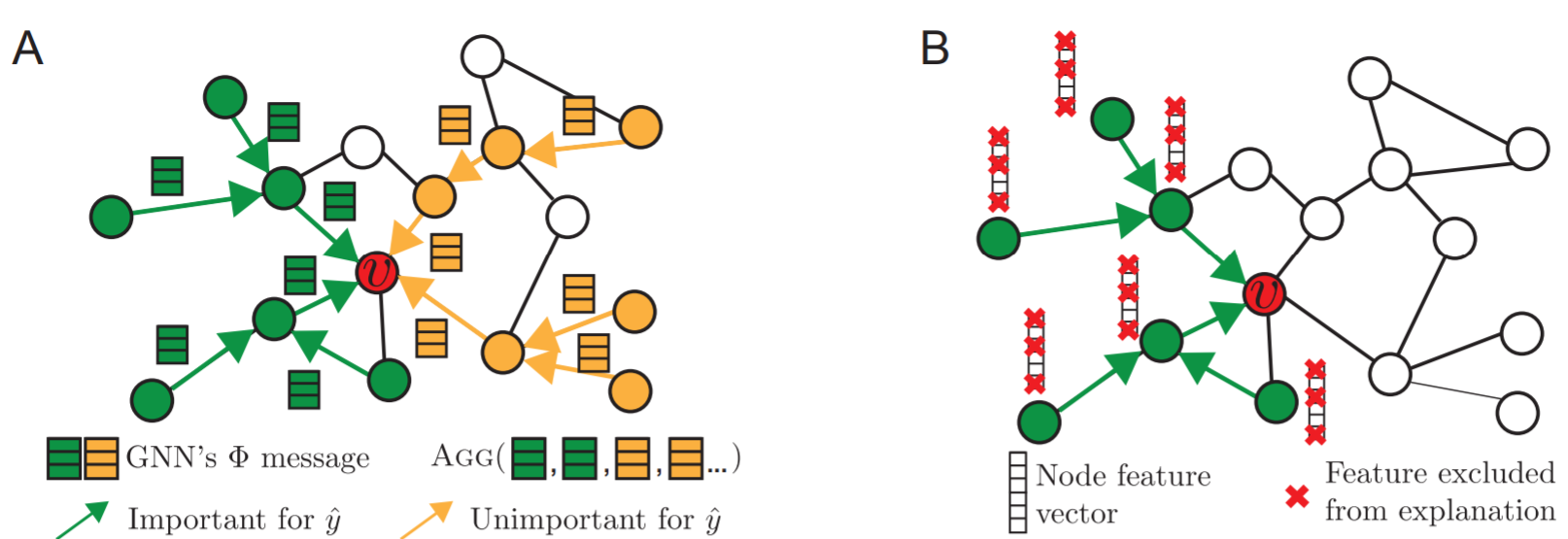
上の右図のように, GNNExplainerは予測に効いた特徴量の決定もします(赤い×が予測にあまり有用でない特徴量). 流れはサブグラフ決定と同じで, 元々の特徴量$X_{S}$にマスクを利用してサブ特徴量$X_{S}^{F}$の獲得を目指します. 式としては以下のようになります. $F$が有用な特徴量を選択するselectorです.
X_{S}^F = X_{S} \odot F \\
F \in\{0,1\}^{d}
よって学習するのは, マスク$F$となります. 両方を考慮した下式を, GNNExplainerは同時最適化します.
\max _{G_{S}, F} M I\left(Y,\left(G_{S}, F\right)\right)=H(Y)-H\left(Y | G=G_{S}, X=X_{S}^{F}\right) \tag{6}
シンプルな選択法として, GNNの重み行列に応じて, 値が小さい特徴量は選択しないという手法が考えられます. しかしこれでは, 本当は有用なのに重み行列の値が小さい特徴量を選択できないので, すべてのサブ特徴量に関して周辺化を行い[(参考)] (https://arxiv.org/abs/1702.04595),学習中にモンテカルロ推定を用いてサンプルします.
また, 誤差逆伝搬の際に(6)の勾配をマスク$F$に流すために, 再パラメータ化トリックを用います.具体的には, 確率変数Xを以下のように再パラメータ化します($Z$は経験分布に対する$d$次元の確率変数で,$K_{F}$は選択する特徴量の上限です).
X=Z+\left(X_{S}-Z\right) \odot F \text { s.t. } \sum_{j} F_{j} \leq K_{F}
ここらへんは良く理解できてないです
Experiments Setup
実験についてここから触れていきます.
使用するデータセットは以下の3つです.
-
Synthetic Datasets
- 著者自作のデータセットです. 以下の図のような構成になっています.
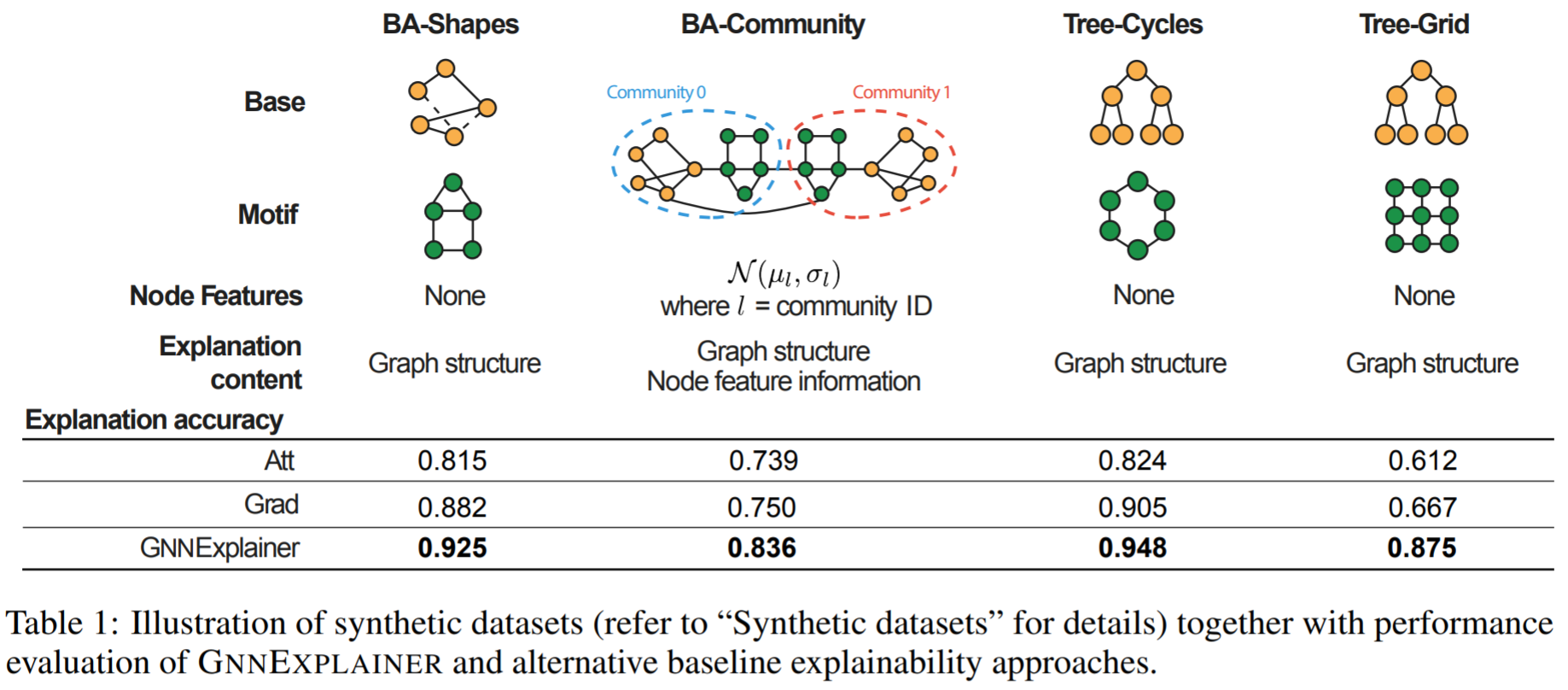
- 一番左のBA-shapesというのは,Baseのグラフとしてscale-freeなネットワークモデルの1つであるBAモデルを作成し, motifとして家(house)のネットワークをbaseのノードに対してランダムに取り付けます. ラベルの種類としては, 家のトップノード, ミドルノード, ボトムノードと, baseのノードの4種類です.
- 他の自作データセットも作成の流れは同様で, ネットワークの"base"があり, "motif"がランダムに取り付けられます. motifをベースにラベルが決まっているので, GNNExplainerがこれを取得できるかどうかを実験で確かめています(Figure 3).
- 著者自作のデータセットです. 以下の図のような構成になっています.
-
MUTAG Datasets
- Molecule Graph(分子構造グラフ)のデータセットで, その分子に変異原性があるかどうかを判別するGraph Classificationタスクのモデルを学習し, それに対してGNNExplainerを用いています(Figure 4).
-
Reddit Bianary Datasets
- redditのスレでのやりとりを集めたデータセットです. タスクはGraph Classificationで, そのグラフがOnline DiscussionかQuestion Answeringかのどちらのスレッドを表しているかを判別するGNNを学習し, GNNExplainerで説明を作成しています(Figure 4).
- ノードの1つ1つがユーザーを表し, エッジはあるユーザーからあるユーザーへコメントが送られたなら, 結ばれています. Online Discussionの有名なsubredditとしてはr/atheism, Quesion Answeringとしてはr/IAmAなどが有名?です. 2chとかでいう,「○○で働いてたけど, 質問ある??」みたいな感じですね
- redditのスレでのやりとりを集めたデータセットです. タスクはGraph Classificationで, そのグラフがOnline DiscussionかQuestion Answeringかのどちらのスレッドを表しているかを判別するGNNを学習し, GNNExplainerで説明を作成しています(Figure 4).
グラフニューラルに対する説明法の提案はこの論文が初めてだと思いますが, 比較手法として勾配ベースの説明と, Attentionベースの説明を使用しています. 余談ですが, 自然言語処理モデルで内部挙動を示していると考えられているAttentionですが, Attention is not Explanationという論文も出ています. さらに余談ですが, これを否定する, Attention is not not Explanationという論文も出ています.
MUTAG, Reddit Binary Datasetsはここからダウンロードできます.
Results
結果画像は3枚, 自作データセット・MUTAG,REDDIT・サブ特徴量抽出の結果3つです.
自作データセットの説明結果
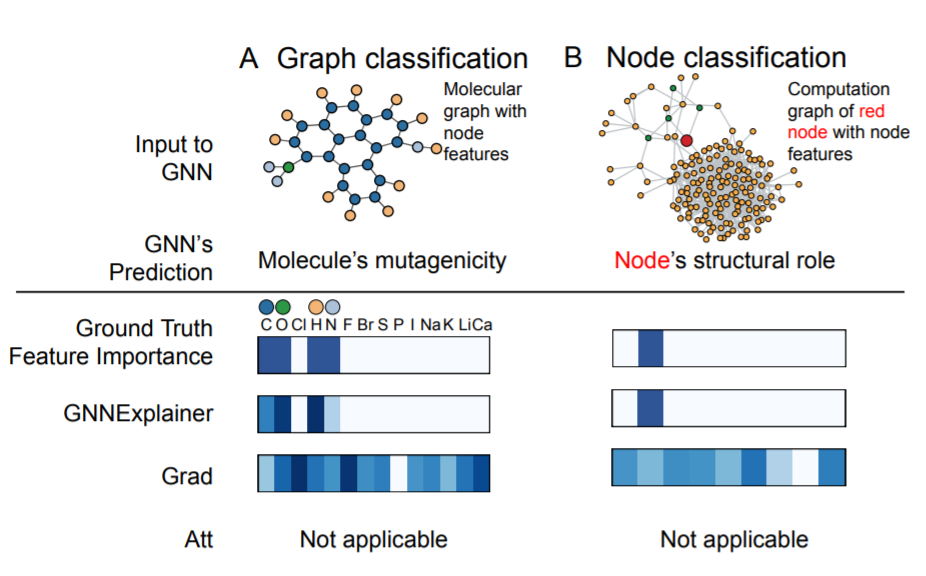
下図が結果です. 赤いノードが予測したノードで, その予測のキモとなったサブグラフを各手法は出力します. 例として左上のBA-shapesに対する説明を見てみると,他手法と比べて分類の鍵であるmotifの家構造(ground-truth)を取れているのがわかります. その他の自作データセットに対する結果も良い出来です.
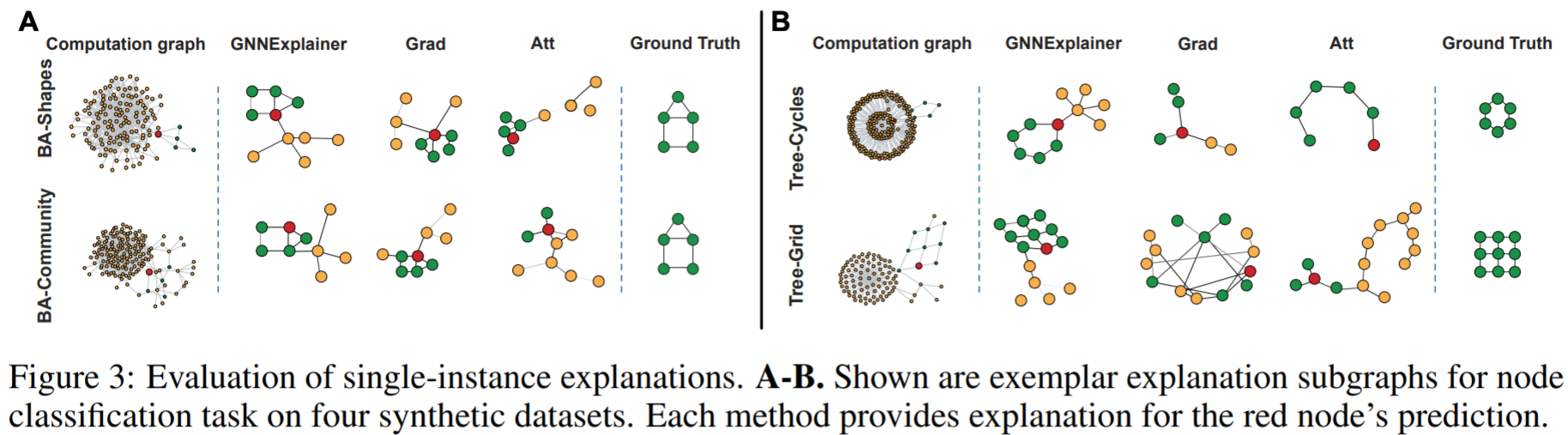
Graph Classificationの説明結果
次がGraph Classificationタスクに対する説明結果です. 上2つがMUTAGの結果,下2つがREDDITの結果です.
MUTAGのground-truthであるring構造(これがあると変異原性がある??)と$NO_2$のgroupがGNNExplainerはサブグラフとして取れています. 変異原もいろいろあるっぽく, ground-truthが本当に正しいのか等はわかりません. 化学に詳しい人教えてください.
REDDITの方は, 左下がOnline Discussionのグラフで, 右下がQuestion Answeringのグラフです. Online Discussionはある1つのトピックに対して多くの人がコメントするスレ, Question Answeringは1人または数人がどんどん質問に答えていくスレであるので, ground-truthが下図のようにそれぞれなっており, それに対してGNNExplainerは良い感じにサブグラフを取れているという主張です.
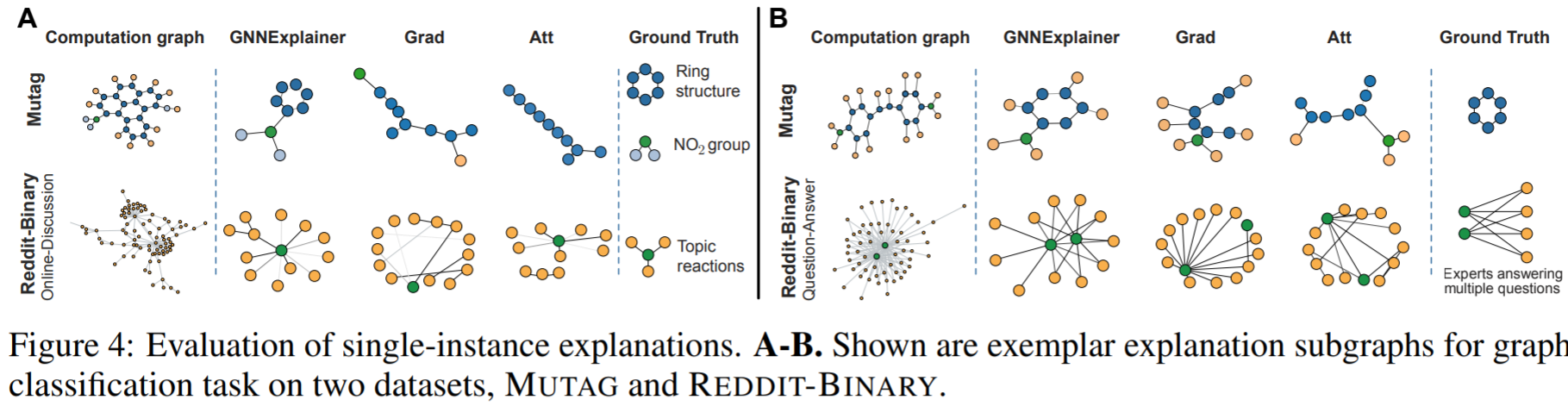
予測に重要であったサブ特徴量の獲得
ラストがサブ特徴量抽出の結果です.左がMUTAGからの1インスタンス, 右が自作データセット1インスタンスに対する結果です. GNNExplainerがGradientベースの手法と比べて, Ground-Truthにかなり近い特徴量の重量度を獲得できています. Attentionベースの手法はサブ特徴量獲得には利用できないので, この図には出てきません.
ちょっと触る
原著の方のコードはここにあります.
クローンして, Google Driveに置いておき, Google Colab上で実行しました. 実行したファイルをここに置いておきます.
自作データセットの1つ, BA-shapesのタスクに対してGNNExplainerを使ってみました. Tensorboardを利用しているので, サブグラフの結果を載せておきます.
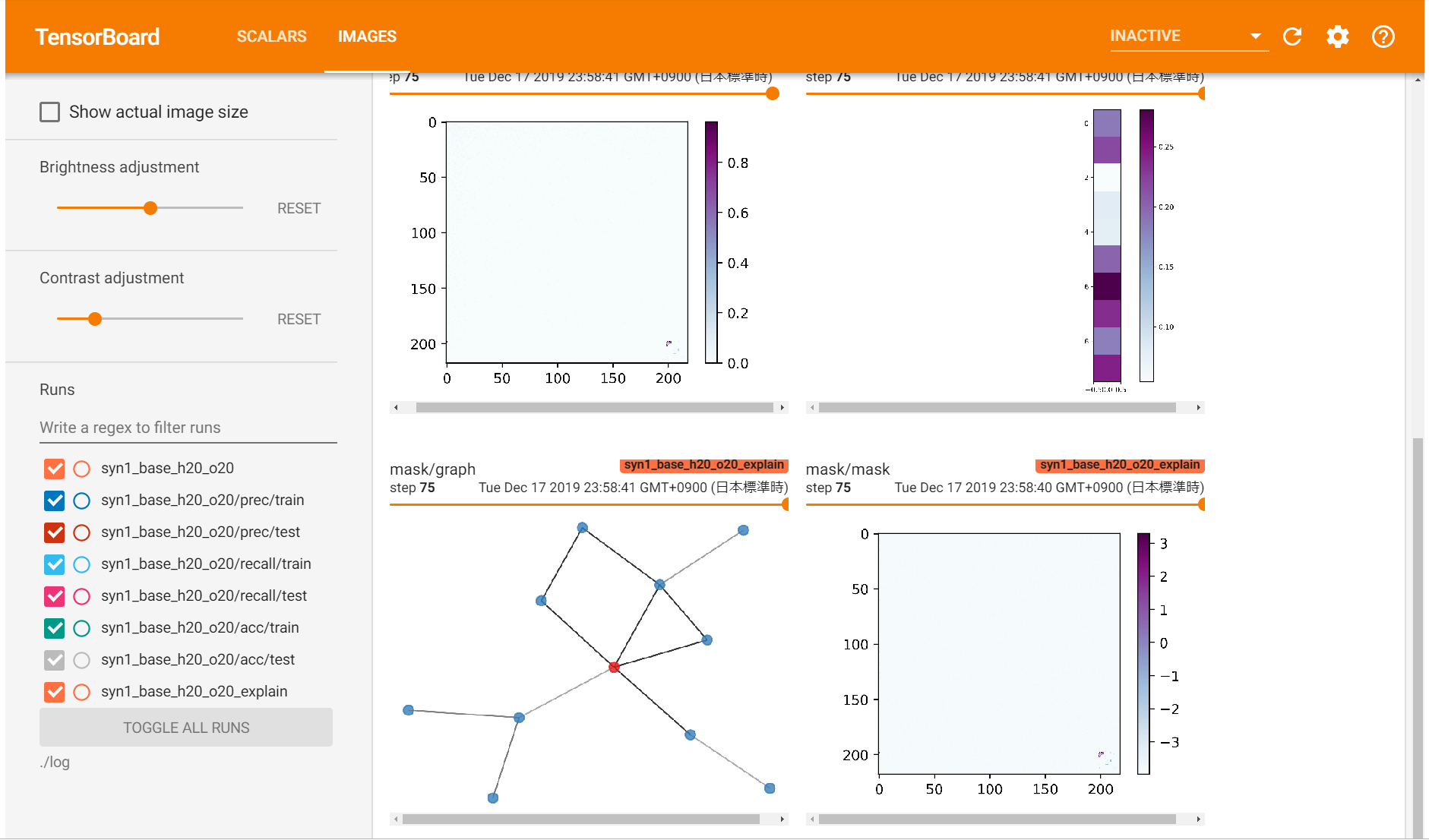
motifの家構造がしっかりと取れています.
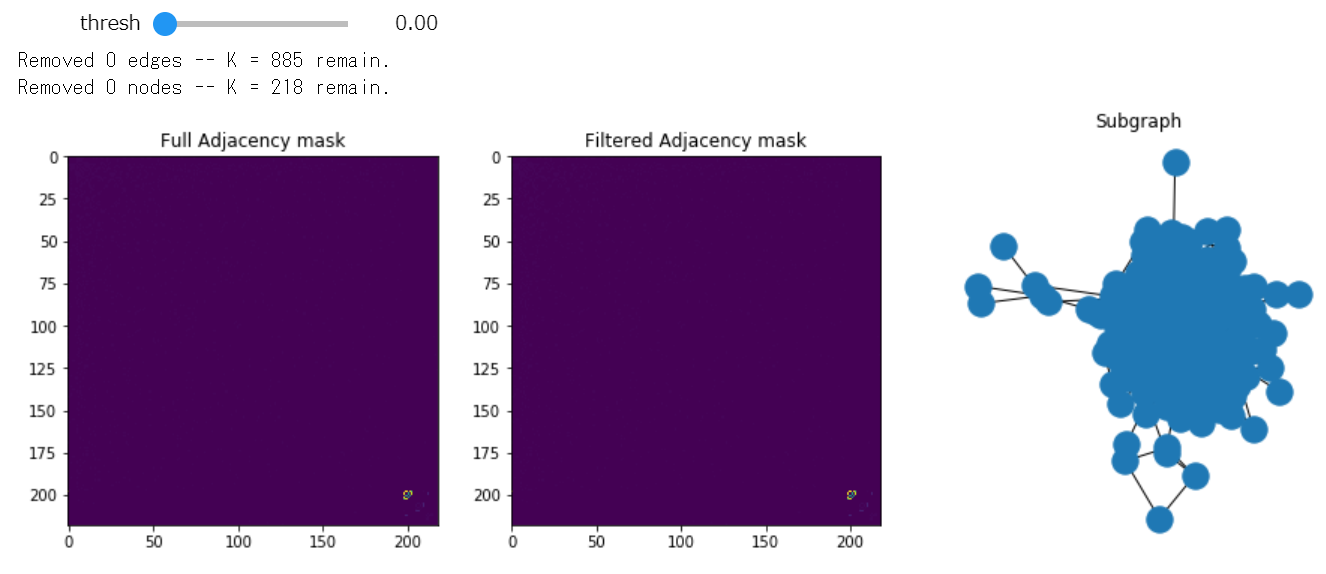
また, ノートブック上でインタラクティブに使えるようにもなっています. threshからしきい値を変更でき, すぐにそれに応じたグラフが出力されます.
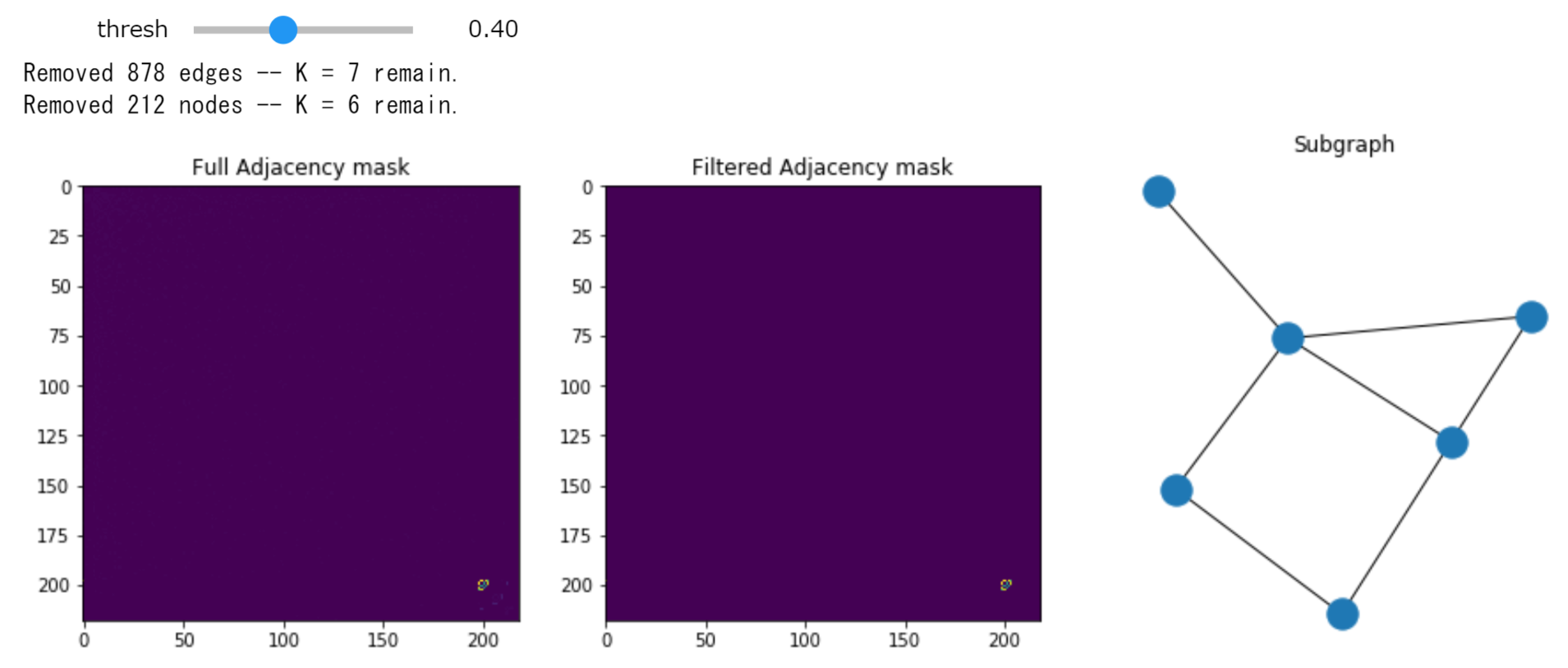
threshを0にしてみると, すべて残すことになるので, 以下のようになります(多くてぐちゃぐちゃ).
Conclusion
GNNに対する説明法として, GNNExplainerというアルゴリズムを提案したというのが本論文でした. この論文がおそらくGNNに対するmodel-agnosticな説明法としては初で, Node Classificationに限らず, GNNにおける別タスクにも適応可能な手法となっています.
最後まで読んでくれてありがとう
良いクリスマスを!