確率変数に関するイェンセン(Jensen)の不等式を、例を用いて直感的に理解してみようという記事です。
$x$を確率変数、$p(x)$をxの確率密度関数とすると、その期待値$E[x]$は
E[x] = \int xp(x)dx
と表現されます。このとき、上に凸な関数 $f(x)$ について、
f(E[x]) \ge E[f(x)]
が成り立つことを、 イェンセン(Jensen)の不等式と呼びます。この証明は既に色々なところで解説(例えばこちら)されていますのでここでは省略します。
この不等式 $f(E[x]) \ge E[f(x)]$ を直感的に理解するために、乱数を用いた例をグラフで表現してみます。
まず、xが正規分布に従う確率変数だとして、そこから発生する乱数を作ってみます。また、そのxを $f(x)=-x^2+10$ という上に凸な関数で変換します。
下記のグラフの上部にあるヒストグラムが正規分布に従うxの分布で、右側にあるヒストグラムが$x^2$が従う分布です。
つまり、イェンセンの不等式は下記の赤い丸(期待値をとってから、つまり上のヒストグラムの平均をとってから、 $f(x)$ で変換)の方が、緑の丸($f(x)$で変換してから期待値を取る、つまり右のヒストグラムの平均値) よりも大きいことを示しているのです。

xの分布である正規分布の平均をずらしてアニメーション化してみたものが下記です。どの場合も緑の丸が、赤い丸より下にあることがわかります。

この不等式、何がいいの???
イェンセンの不等式
f(E[x]) \ge E[f(x)]
は、$f(E[x])$を最大化したいが、この関数がなにものであるか不明であるとき、$E[f(x)]$であれば計算できるのであれば、$E[f(x)]$が$f(E[x])$の下限として扱えるため、計算可能な$E[f(x)]$の最大化を行うことで、本来のターゲットである$f(E[x])$の最大化を行えることです。
よく使われるのは $\log(\cdot)$が上に凸な関数であるため、
log \int p(x)f(x)dx \ge \int p(x) log f(x)dx
のように、$\log(\cdot)$を積分の中に入れて計算できるようにするといったことです。
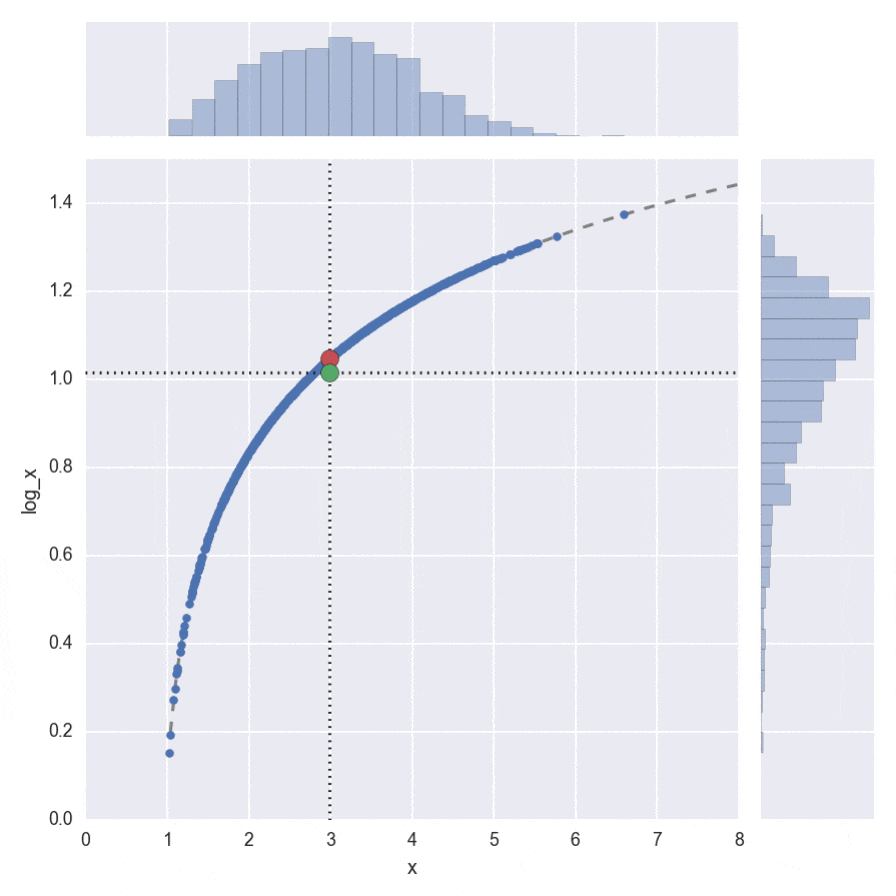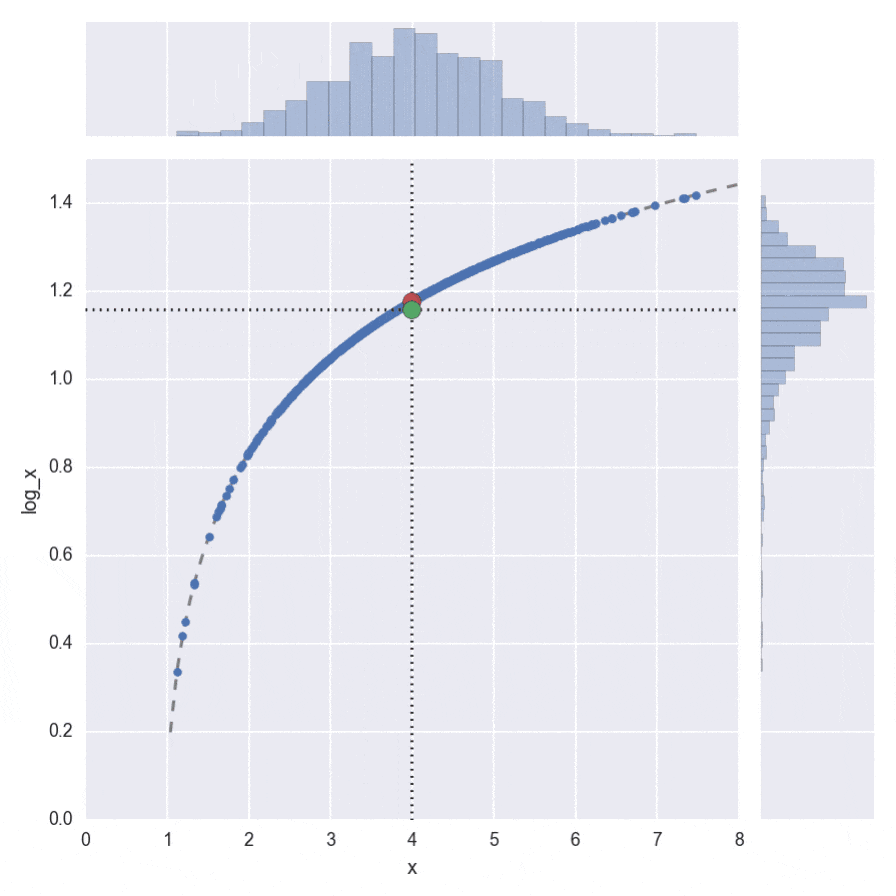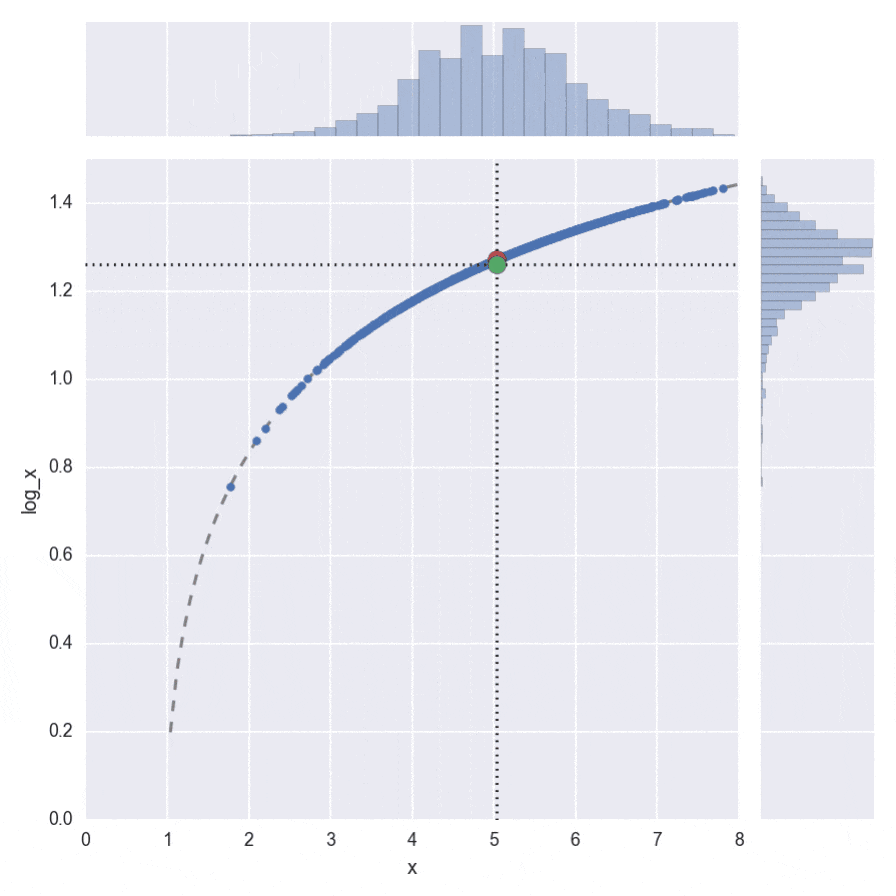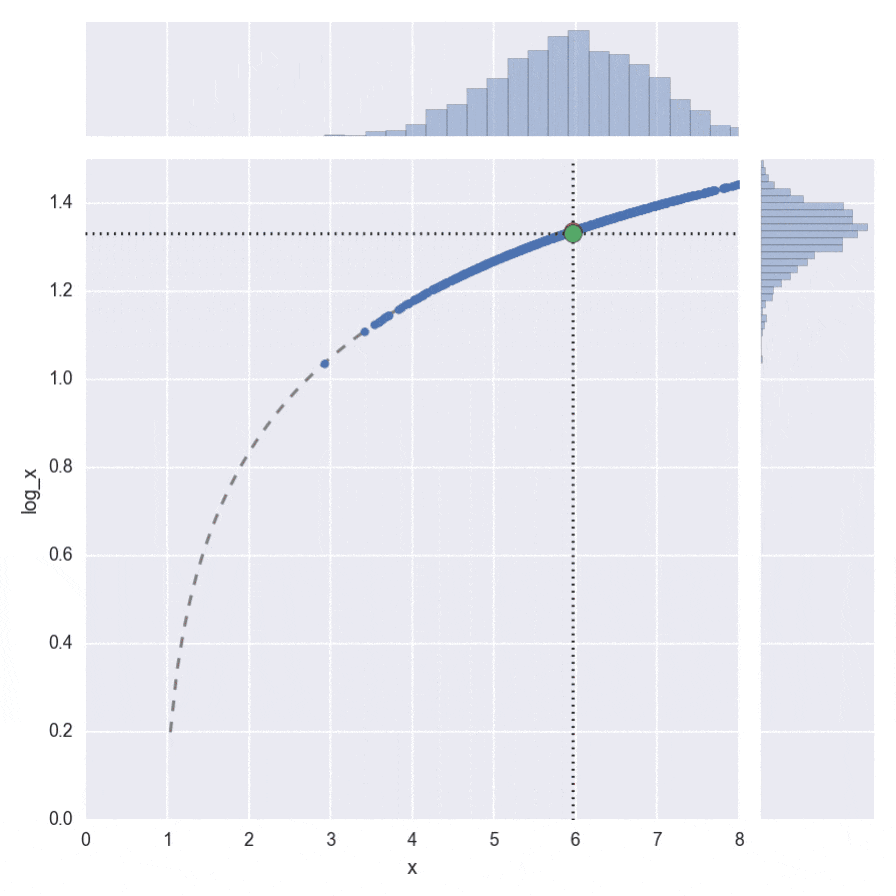
ちょっとわかりづらいですが、$\log(\cdot)$の場合のアニメーションがこちらです。
右側のヒストグラムを見ると下側に歪んでいるので、平均値が下にずれることが感覚的にもわかります。その分、緑の丸が、赤い丸より下になってしまうことが見て取れます。
参考
1.8 確率変数の不等式 1
http://mcm-www.jwu.ac.jp/~konno/pdf/statg-1-8r.pdf
この記事で使ったグラフを記述したPythonコード
https://github.com/matsuken92/Qiita_Contents/blob/master/General/Jensens-inequality.ipynb