GoogleのExplainable AIを構成する技術について

先月(2019/11)にGoogleが"Explainable AI"という名称で新しいサービスのリリースを宣言しました(Google Explainable AIのページ) このサービスは学習済みの予測モデル (特にTensorFlowのモデル) を用いて、予測結果が入力データのどの要素によって影響を受けているか、その影響度合いを返すことができるという機能です。

近年、特にDeep Learningを中心とした複雑な機械学習の予測モデルでは「なぜそのような結果が得られたのか、モデルがブラックボックスで説明ができない」という指摘があります。これらの指摘に対する回答として説明可能なAI(Explainable AI、あるいは省略されてXAIとも呼ばれる)と言われる技術が複数開発されています。

Google の Explainable AI の技術概要を説明したドキュメント(Introduction to AI Explanations for AI Platform)には、モデルにおける説明変数の寄与度(feature attribution)の算出に、 Sampled Shapley¹ と Integrated Gradients² という2つの手法を用いたという記載があります。この記事では、この2つのアルゴリズムの原論文の内容を説明します。

※ なお、attribution は、広告分野では、複数メディアでの広告効果を配分する文脈でそのまま「アトリビューション」と言われたりします。日本語では本来「帰属」といったあたりの意味ですが、いずれもしっくりこないので、この記事では「寄与度」としました。

変数の寄与度の基本的な考え方

$K$次元の説明変数 $\boldsymbol{x}=(x_1, ..., x_K)$ を入力し、目的変数 $y$ の値を出力する学習済み予測モデル $y=F(\boldsymbol{x})$ があるとします。ここで、ある特定の値 $\boldsymbol{x}$ を入力した場合に、説明変数の各次元 $k$ の出力へどの程度影響を与えているか、その寄与度(feature attribution)を考えます。つまりここでの寄与度とは、説明変数の値 $\boldsymbol{x}$ ごとに決まる前提です。

問題を単純化するために、いま説明変数は $A, B, C$ の3変数でありいずれも$0/1$変数であるとします。またモデル $F$ は回帰モデルであり、目的変数 $y$ は連続値を取ると考えます。いま、この3つの説明変数がすべて$1$とした場合 $(A, B, C) = (1, 1, 1)$ に得られた予測値が、すべて$0$とした場合 $(A, B, C) = (0, 0, 0)$ と比較して、どの変数がどの程度効いているか？という問題設定を考えます。変数の寄与度の算出における「比較の基準」のことをベースライン(baseline)と呼びます。

変数$A$の寄与の大きさはどれくらいでしょうか？ たとえば単純には変数$A$の値を$0$から$1$に変更したときの目的変数の変化を考えたら良さそうです。1変数しかなければ話は単純ですが、3変数のモデルの場合は、単にAの値だけではなく、ほかの2つの変数値によっても目的変数の値が変わります。

以下、Explainable AI Whitepaper³ に記述のある具体例を考えてみましょう（ただしスケールを改めています) ここで、説明変数の値が $(A, B, C) = (0, 1, 1)$ となる場合を $\{ B, C\}$ と書くことにします。つまり、変数の状態を、値が1である(予測に参加している)変数の集合として表すものとします。

ベースラインと寄与度算出対象の予測値が次のようになるとします。

• 寄与度算出対象予測値 $y = F(\boldsymbol{x}) = F(\{A,B,C\}) = 1$
• ベースライン予測値 $y' = F(\boldsymbol{x'}) = F(\{\}) = 0$

また、それぞれの変数が中途半端に予測に参加するケースでは次のような予測値になるとします。

• $F(\{A\}) = 0.1$
• $F(\{B\}) = 0.2$
• $F(\{C\}) = 0.3$
• $F(\{A,B\}) = 0.6$
• $F(\{B,C\}) = 0.7$
• $F(\{A,C\}) = 0.9$

A以外の変数(B,C)が0である場合には、Aの値による予測値の変化は、

F({A}) - F(\{\}) = 0.1

となりますが、B,Cがいずれも1の場合には、

F(\{A,B,C\}) - F(\{B,C\}) = 0.5

となります。一般に、ある変数が予測に参加することで予測値に加わる差分は、他の変数の参加状態に依存します。

この状況を解消する方法として、注目している変数以外のすべての変数について、考えうるすべてのケースを網羅したうえで、すべてのケースで計算した差分の平均を算出するのが、妥当な寄与度の算出手法として考えられます。

「すべてのケースを網羅して平均する」という点をもう少し具体的に言うと、どの変数も参加していない状態から、ランダムに1変数ずつ順に予測に参加して、最終的に全変数が予測に参加するとした場合に、注目している変数が加わることによる目的変数の変化の期待値を寄与度と考えるとすることに相当します。

言葉で書くとちょっとわかりにくいので... 上記のA,B,Cの3変数のケースで考えてみましょう。
1変数ずつ順番に予測に参加するケースは全部で$3!=6$通りあります。ちょっとごちゃごちゃしますが、実際にすべてのケースを以下に書き下し、Aが参加する場合の目的変数の値の変化を「Aの寄与の算出」欄に書いてみます。

加わる順序	Aの寄与の算出
$A \to B \to C$	$F(\{A\}) - F(\{\}) = 0.1 - 0 = 0.1$
$A \to C \to B$	$F(\{A\}) - F(\{\}) = 0.1 - 0 = 0.1$
$B \to A \to C$	$F(\{A,B\}) - F(\{B\}) = 0.6 - 0.2 = 0.4$
$B \to C \to A$	$F(\{A,B,C\}) - F(\{B,C\}) = 1 - 0.7 = 0.3$
$C \to B \to A$	$F(\{A,B,C\}) - F(\{B,C\}) = 1 - 0.7 = 0.3$
$C \to A \to B$	$F(\{A,C\}) - F(\{C\}) = 0.9 - 0.3 = 0.6$
全ケースの平均 $\phi_A(F)$	$0.3$

最後に平均値を計算しましたが、この値 $\phi_A(F)$ が「どの変数も同じ確率でランダムに予測に参加する場合に、対象となる変数の参加による予測値の増加の期待値」であり、これをAの寄与度とみなすことができます。

同様にして、$B, C$ の寄与度は $0.25, 0.45$ となります。他の変数の参加条件を同程度にランダムに考えているため、他の変数の影響をフェアに取り扱った指標といえるでしょう。ところでこの寄与度 $\phi_A(F), \phi_B(F), \phi_C(F)$ の和は $0.30 + 0.25 + 0.45 = 1.0$ となりこれは予測値のベースラインとの差異 $y - y'$ と等しくなります。

シャープレイ値と4つの公理

実はこのように計算した値は、(協力)ゲーム理論の分野で**シャープレイ値(Shapley value)**と呼ばれる値と全く同じものになります。

変数の寄与度の場合は、変数が予測に参加するかどうかという観点ですが、シャープレイ値とは、複数のプレイヤーが同時に参加するゲーム上で定義されるものです。ここで、全プレイヤーの集合を$N$と書きます。また、このプレイヤーの部分集合 $S$ がゲームに参加する(提携と呼ばれる)場合に 、「ゲームの値」を返す関数 $v(S)$ が定義されているとします。

「ゲームの値」とは、例えば複数のプレイヤーが協力してお金を稼ぐタスクがある場合に、同時に参加して稼ぐことのできる金額のようなものを考えると想像しやすいかもしれません。この値は複数のプレイヤーの提携によるものであり、一般には各プレイヤーの寄与の単純な足し合わせとはなりません。そのため、個々のプレイヤーがどの程度ゲームに対して貢献しているかは、ほかのプレイヤーの参加状態によって異なることになります。シャープレイ値は、他のプレイヤーの参加状況も加味して、対象のプレイヤーがどれだけ貢献したかを公平に評価する方法の一つです。

実は、シャープレイ値は、次の4つの公理を満たします。逆に、シャープレイ値の算出手法は、これらの公理を満たす唯一の値となります（公理の名称・定式化については様々な流儀がありますが、ここでは岡田⁴の記述に準じました）。ここで、$N$は全プレイヤーの集合、$v(S)$はプレイヤーの部分集合$S \subset N$のゲームの値を返す関数、$\phi_i(v)$は関数$v$のもとでのプレイヤー$i$のシャープレイ値です。

[1] パレート最適性 (Efficiency または Completeness)
すべてのプレイヤーのシャープレイ値を合計すると、全プレイヤーが参加した場合のゲームの値となる。

\sum_{x \in S} \phi_i(v) = v(S)

[2] 対称性 (Symmetry)
2人のプレイヤー$i, j$が参加する・しないの役割を変えてもゲームの値が変わらない、つまり $i, j$ を含まないプレイヤー集合 $S \subset N$ に対して $v(S \cup \{i\}) = v(S \cup \{j\})$ となる場合、それぞれのプレイヤーのシャープレイ値は等しい

\phi_i(v) = \phi_j(v)

[3] 加法性 (Additivity あるいは Linearity)
2つのゲーム$v, w$の値を合計した別のゲーム$v + w$がある場合、合計したゲームのシャープレイ値は、2つのゲームのシャープレイ値の合計になる。

\phi_i(v + w) = \phi_i(v) + \phi_i(w)

[4] ナルプレイヤーに対する性質 (Dummy)
どんな状況において参加しても、ゲームの値が変わらないプレイヤー$i$のシャープレイ値はゼロである。

これは、やや細かい話のように見えますが、微分可能なモデルでも同様の性質を満たす指標として、変数の寄与度を算出することになります。

シャープレイ値を実際のモデルに適用する

実際のモデルは2値変数ではないので、次のような考え方をします⁵。説明変数 $\boldsymbol{x}$ は $k$次元の変数 $(x_1, x_2, .. , x_k)$ であり、モデル $F(\boldsymbol{x})$ に入力して予測値 $y$ が得られるとします。

これらの変数ごとの寄与が知りたいのですが、そのために比較元であるベースライン $\boldsymbol{x'}$ を考えておきます。通常、数値変数の場合では $\boldsymbol{x'} = (0, ..., 0)$ のように、すべての変数が $0$ などの「無意味」とされる値をとるようにおきます。画像であれば真っ黒画像などがベースラインの代表例となります。ただし「無意味」と考える入力であれば任意に設定してもよく、逆に問題に適したベースラインを考えるべきというのがこの手法のポリシーです。

説明変数 $\boldsymbol{x} = (x_1, ..., x_K)$ の次元ごとに、0または1の値をとるフラグ変数 $\boldsymbol{z} = (z_1, ..., z_K)$ を考えます。この変数は

• $z_k = 1$ の場合は、$k$次元目の変数に対象の説明変数値 $x_k$ を使う。
• $z_k = 0$ の場合は、$k$次元目の変数にベースライン $x'_k$ を使う。

この場合に、$\boldsymbol{z}$ から $\boldsymbol{x}$ を得る関数 $\boldsymbol{x} = h(\boldsymbol{z})$ を定義しておけば $\boldsymbol{z}$ を入力とするモデル $F(h(\boldsymbol{z}))$ を構成できます。このモデルでは先ほどのシャープレイ値で仮定したように、0/1 値を説明変数としてとり、ベースラインとしてすべて0、比較対象としてすべて1が対応するため、同様にシャープレイ値の計算手順に基づいた変数の寄与を算出できます。

シャープレイ値の計算方法とその限界

原理的には、変数が増加した場合でも律儀にすべての変数の参加順序を書き下せばシャープレイ値を算出でき、変数の寄与度が求まることになります。しかし冷静に考えると、変数の数が非常に多い場合のシャープレイ値の算出は大変です。

目的変数の値 $y$ に対する変数 $x_k$ の寄与を $\phi_k(F)$ とすると、ガチな計算では、全変数の順列 $O$ について変数 $x_k$ が $O$ に加わる直前でのプレイヤーの集合を $P_k^O$ とすると、

\phi_k(F) = \frac{1}{K!} \sum_{O} [v(P_k^O \cup \{k\}) - v(P_k^O)]

ただしこれは変数の数 $K$ に対して $K!$ 通りの順列の数え上げが必要であり大変です。実際には、注目しているプレイヤーが加わる直前のプレイヤーの値は、そこまでの加入の順序に依存せず組み合わせだけを考えればよく、実際の計算量は$K!$から$2^K$ のオーダーに減らすことができます。しかしまだ指数オーダーであり、非常に数が多い場合にはまだ大変です。

サンプリングによる方法

計算量爆発を避けるため、Google の Explainable AI では Sampling Shapley¹ というランダムサンプリングの方法を採用しているとのことです。以下では、その手法の原論文からそのサンプリング方法を説明します。

アイデアは次の通りです。元々のシャープレイ値は、予測に変数が加わるすべてのパターンが等確率で発生することを前提においています。このことから、変数のすべての参加順序$K!$通りからランダムに発生させて、変数の寄与を計算し、これを一定回数繰り返して計算された寄与のサンプル平均 $\hat{\phi}_k(F)$ をシャープレイ値とするものです。

ここでランダムに発生させた順列 $O$ について、変数 $x_k$ が $O$ に加わる直前でのプレイヤーの集合を $P_k^O$ とすると、

\hat{\phi}_k(F) = \hat{\phi}_k(F)  + \frac{1}{M} [v(P_k^O \cup \{k\}) - v(P_k^O)]

このサンプリングを$M$回繰り返して、シャープレイ値の推定値を得ます。

これではちょっと説明がわかりづらいかもしれないので... 以下に具体的なケースを示します。今、変数が$A, B, C, D, E$ の5つあるとして、ランダムに加入順序を生成します。この順序が $D \to C \to A \to B \to E$ であるとします。

まず次の値を算出しておきます。

• $F(\{\})$ ... ★
• $F(\{D\})$
• $F(\{D,C\})$
• $F(\{D,C,A\})$
• $F(\{D,C,A,B\})$
• $F(\{D,C,A,B,E\})$ ... ☆

☆は全プレイヤー参加状態、★はベースラインであり、これは事前に一度計算すれば十分です。それぞれのプレイヤーが参加するタイミングの差分を算出し、差分の合算値に累積します。

• $\hat{\phi}_D(F) = \hat{\phi}_D(F) + \frac{1}{M} (F(\{D\}) - F(\{\}))$
• $\hat{\phi}_C(F) = \hat{\phi}_C(F) + \frac{1}{M} (F(\{D,C\}) - F(\{D\}))$
• $\hat{\phi}_A(F) = \hat{\phi}_A(F) + \frac{1}{M} (F(\{D,C,A\}) - F(\{D,C\}))$
• $\hat{\phi}_B(F) = \hat{\phi}_B(F) + \frac{1}{M} (F(\{D,C,A,B\}) - F(\{D,C,A\}))$
• $\hat{\phi}_E(F) = \hat{\phi}_E(F) + \frac{1}{M} (F(\{D,C,A,B,E\}) - F(\{D,C,A,B\}))$

これを 事前に決めた回数繰り返して合算した値をシャープレイ値とします。個人的には、そんなシンプルでいいのかという気もしますが、文献では許容誤差から適切な繰り返し回数 $M$ を設定することができ、その回数だけサンプリングすれば、設定した誤差の範囲内に収まることが示されています。

Google の Whitepaper でも次のメリットがある点が指摘されています。

• 説明変数の次元に対して、計算量が線形のオーダーで増加すること。
• 算出される寄与度に対する許容誤差に基づくサンプリング回数を設定できること。

なお、サンプリングを用いずシャープレイ値の計算量を減らして変数の寄与度を求める別の手法として SHAP (SHapley Additive exPlanations)⁵ という方法があります。SHAPでは、シャープレイ値の算出にさらに別予測モデルを援用する考え方になります。その考え方と比較すると、Sampling Shapley はハイパーパラメータとなるものが(サンプリング回数以外に) ないため、「寄与度を算出したのに、その意味を説明するために別のモデルの説明をする必要がある」という事態を避けられるというメリットがあるようです。

微分可能なモデルでの代替案

Sampling Shapley が適用できる予測モデルのクラスはかなり広い範囲を網羅しますが、Neural Network のように出力 $y$ の入力 $\boldsymbol{x}$ による微分値 $\nabla_{\boldsymbol{x}} F(\boldsymbol{x})$ が(back propagationなどを通じて)算出できる場合には、微分値を使った(簡易な)方法が存在します。

微分値による寄与度としては、単純には 入力値 $x$ における $y$ の微分値が考えられますが、単に入力値の微分値を採用してしまうと、例えば ReLU のように入力値の微分値がゼロとなってしまい、あまり意味を持たなくなってしまうという問題があります。

Google Explainable AI で採用されているもう一つの手法 Integrated Gradients² は、微分可能なモデルに対する説明変数の寄与度として考えられた手法の1つです。この方法も、対象となる説明変数の値 $\boldsymbol{x}$ の各次元$k$における寄与度を、ベースライン $\boldsymbol{x'}$ との比較で算出する手法です。天下り式ですが、このIntegrated Gradients は次のように算出します。

\textsf{IntegratedGrad}_i(x) = (x_i-x'_i) \int_{\alpha=0}^{1}
\frac{\partial F(\boldsymbol{x'} + \alpha \times (\boldsymbol{x} - \boldsymbol{x'}))}{\partial x_i}

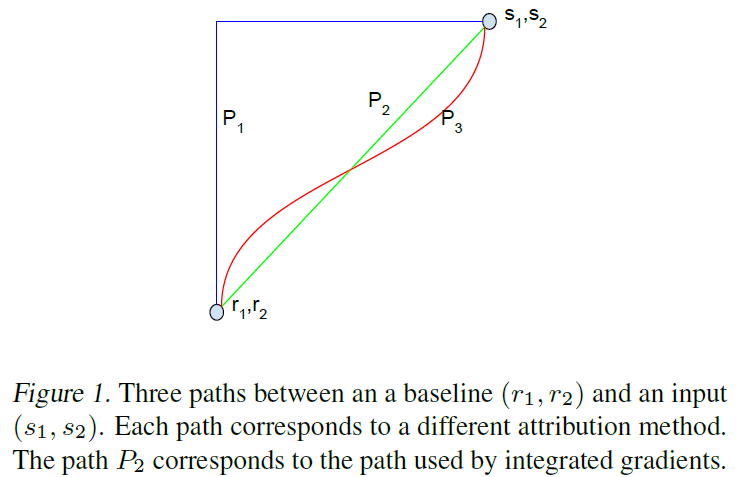
これは変数の値を、ベースラインの値 $\boldsymbol{x'}$ から $\boldsymbol{x}$ まで直線で結ぶ経路を考え、この経路上で対象となる変数の微分値(Gradient)を積分した(Integrated)値となっています。この値の算出には、モデルの出力値の入力値(説明変数)についての微分値が算出できればどのようなモデルに対しても適用できるため、算出過程がモデルの実装に依存しないという利点があります。

またモデル $y=F(\boldsymbol{x})$が、ほとんどいたるところ(全)微分可能であれば、次の式が整理します。

\sum_i{\textsf{IntegratedGrad}_i(x)} = F(\boldsymbol{x}) - F(\boldsymbol{x'})

つまりIntegrated Gradientsで計算された各変数の寄与度をすべての変数で合算すると、注目している予測値とベースラインでの予測値との差異と等しくなります。この性質は、シャープレイ値のところで出た性質である「パレート最適性」と同等です。

なお「ほとんどいたるところ微分可能」とは、特定の点をのぞけば微分可能であるような関数であればOKという意味なので、局所的に(測度0の集合において)微分不可能となる困った点を含むReLUのようなActivation Functionを使うNeural Networkでも適用可能です。

微分可能モデルでの公理系

ところで、全微分可能な関数の性質として、積分経路をどのようにとっても実はこの式が満たされます。例えば Integrated Gradient の前提では P2 の経路を使いますが、P1, P3 でも積分値はおなじになります。この任意の経路による積分を「積分経路による方法」と呼ぶことにします。

では、なぜ Integrated Gradients では直線的な経路を採用しているのでしょうか。ここで一旦別の話にワープして置き去りにされたシャープレイ値の公理系が再来します。実は、このように $x_0$ から $x$ までの経路で微分値を積分して得られる寄与度の算出手法のうち、Integrated Gradients は、前述の(集合に基づく)シャープレイ値と同様の4つの公理を満たす唯一の経路であることが証明されています。

1. パレート最適性 (Completeness)
2. 対称性 (Symmetry)
3. 加法性 (Linearity)
4. ナルプレイヤーに対する性質 (Dummy ; 但し現論文では Sensitibity (b)と書かれている)

任意の経路での積分値は対称性を除く性質を満たし、唯一、直線経路のみが対称性を含むすべての公理を満たす経路となります。そのため、Integrated Gradients の提案論文ではAxiomatic Attribution for Deep Network(公理に基づくDeep Networkの寄与度)という表題が与えられています。

Integrated Gradients の実際の実装

実際の Integrated Gradients の計算は、単純な数値積分をすればよいようで、つまり次のように計算します。

\textsf{IntegratedGrad}_i(\boldsymbol{x}) = (x_i-x'_i) \sum_{k=1}^{m}
\frac{\partial F(\boldsymbol{x'} + \frac{k}{m} \times (\boldsymbol{x} - \boldsymbol{x'}))}{\partial x_i}
\times \frac{1}{m}

論文筆者によると、数値積分の区間分割数 $m$ は 30から200程度あれば十分だよとのことです。この計算には、数値積分の区間ごとに、モデルによる予測と、(Neuralの場合はbackpropagationによる)微分値の計算が必要ですが、都合200回程度実施すればOKとのことであり、計算量的にもリーズナブルです。

考察

個人的な印象では、Sampling Shapleyにしても Integrated Gradients にしても比較的実装が容易で、特に複雑なことはしていないという印象があります。Googleがこれらの手法を採用したことの理由についてを私見を挙げてみます。

1つには、算出手法に一貫性があることがあると思われます。

いずれの方法でも、シャープレイ値がみたすべき公理に基づいた指標であり、すべての変数の寄与を合算すると目的変数の差分になる(パレート効率性)ことであったり、変数の役割が同等であれば、寄与も同一である(対称性)ことであったり、寄与度が自然に満たすべき性質を満たしており、算出される指標も説明困難な挙動をできうる限り排除したものになることが期待されます。結果に対する批判の最後の防御として、公理に戻ることができます。

2つには、寄与度の算出に、説明困難な複雑さを導入しないという考え方があるように見えます。

いずれも手法も、サンプリング数や刻み幅といった、算出精度と計算量のトレードオフをコントロールするパラメータをもつものの、必要最小限度であり、チューニングが必要なハイパーパラメータを持たないため、算出された寄与度の算出理由を説明しなければいけなくなるという空虚な堂々巡りを必要最小限度にすべきであるという思惑が感じられます。

3つめとして、算出された寄与度を起点とした実業務オペレーションでの導入のわかりやすさを優先したという観点があると思われます。

Whitepaper³では、出力結果をどのように解釈するか、またステークホルダーに対する説明としてどのように利用すべきであるかという観点の説明に多くを割いています。これらの観点で、結果の理由における考え方・ポリシーを同一の観点のもとに算出された値として統一することで、運用時のわかりやすさを狙ったものと理解できます。

ただし、これらの特徴はドライに解釈すると「これはただのシャープレイ値だ」という見方もあると考えてよいと思います。これらの考え方を基に計算された値は人間の思考過程を考慮したというわけでは決してないため、人間が考えうる説明性の自然さをそこに求めた場合には、結果に対する期待とのギャップが顕著になる可能性があります(Whitepaperでも同様のremarkが多数ある)

その課題を解決できないのか？という話になると、結局「モデルの説明可能性として、現場では何を出せば正解なのだろう？」という根源に戻るのかもしれません。Googleでもびっくりするくらいのシンプルな技術に落ち着いたのは、その問いが実はとても奥深く、試行錯誤の過程にあるということを象徴するものかもしれないと思ったりします。

1. Sasan Maleki, Long Tran-Thanh, Greg Hines, Talal Rahwan, Alex Rogers. Bounding the Estimation Error of Sampling-based Shapley Value Approximation. https://arxiv.org/abs/1306.4265 ... サンプリングによるShapley値を提案した論文。微分可能でないモデルにも適用できる手法。 ↩ ↩²

2. Mukund Sundararajan, Ankur Taly, Qiqi Yan. Axiomatic Attribution for Deep Networks. https://arxiv.org/abs/1703.01365 ... Integrated Gradientsの現論文。Neural Networkなど微分可能なモデルに適用する手法 ↩ ↩²

3. Google. Explainable AI Whitepaper. ↩ ↩²

4. 岡田章. ゲーム理論 新版 ↩

5. Scott Lundberg, Su-In Lee. A Unified Approach to Interpreting Model Predictions. https://arxiv.org/abs/1705.07874 ... SHAP (SHapley Additive exPlanations) を提案した論文 ↩ ↩²