背景
- 前回: Computational Optimal Transport 精読会 記録 (#9: 3.7)は5/23に開催,今回は近く5/28に開催したのだけど,体調を崩してしまったので遠隔から参加(遠隔は難しくて微妙)
- 職場でCOTを読んでおり,{自己満足,復習,将来のため}などの理由で記録をしている
今回の範囲の内容
- ついに§4に突入してエントロピー正則化をやっていく
§4.1 Entropic Regularization
-
Coupling matrix $\mathbf{P}$の離散エントロピーを定義する: $H(\mathbf{P})=-\sum_{i,j} (\log \mathbf{P}_{i,j} - 1)$
- 行列二階微分(ヘッシアン)を計算すると,$\log$のところの$\mathbf{P}_{i,j}$が対角成分だけ残るので,$\mathrm{diag}(1 / \mathbf{P}_{i,j})$になる
- これの半正定値性を確認するため,任意の(非ゼロ)ベクトルを左右からかけて考えるか,正方行列の二乗で書けるので半正定値になっている.また$\mathbf{P}_{i,j} \leq 1$なので,1-strongly concaveになっている(自信なし)
-
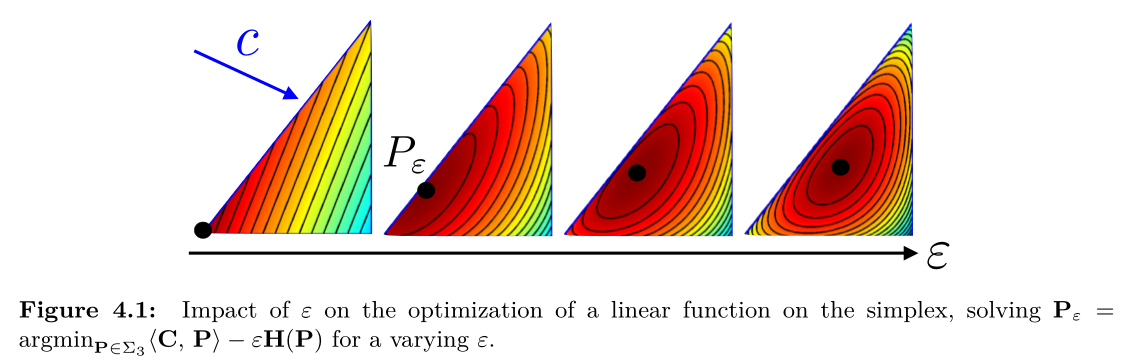
これを正則化項に利用する問題を $L^\epsilon_C(a, b)$のように表す
-
意味(効果): 3次の確率単体を可視化したものと見る
Prop 4.1
-
$\epsilon$に関する最適化問題の収束性を議論し,特に$\epsilon \to 0$と$\epsilon \to \infty$を主張
-
証明
- 分からない
-
(メモ)
- $U(a, b)$が閉じているため,有界閉空間
- これは点列コンパクトである (=収束する部分列を取ることができる)
- このあたりから挟み込むと収束性が示せる($\epsilon\to 0$の場合)
- $\epsilon\to \infty$は知らん
-
この辺を真面目に議論するためには集合と位相の知識が必要
KL-divergence
- 次の形でKL-divergenceを定義する
- よく使うKLの形ではないけど,Bregmanなんたらとかと関係がある(たぶん)
- ただし$K$はギブスカーネルっぽい感じの重み: $\mathbf{K}_{i,j}=\exp(-C_{i,j} / \epsilon)$
$$KL(\mathbf{P}\mid \mathbf{K}) = \sum_{i,j} \mathbf{P}_{i,j} \log\left(\frac{\mathbf{P}_{i,j}}{\mathbf{K}_{i,j}}\right) - \mathbf{P}_{i,j} + \mathbf{K}_{i,j}$$
- KLを小さくするような写像を定義する
$$\mathbf{P}_\epsilon = \mathrm{Proj}_{\mathbf{U}(\mathbf{a,b})}^\mathbf{KL}(\mathbf{K}) = \arg\min_{\mathbf{P}\in \mathbf{U}(\mathbf{a,b})} \mathbf{KL}(\mathbf{P}\mid \mathbf{K})$$
- おそらくどこかで使います
Next
- 6/11に開催予定,§4.2はかなり長いので分割になるであろう